理论介绍:
蒙特卡洛方法(Monte Carlo Methods),简称M-C法,又称随机抽样技巧法,其实质是利用随机数,可以说是把某个未知值取作某种概率分布或者概率过程的未知参量,然后根据无作为标本抽出法对它进行统计、推定的一种方法。这个未知值不一定是概率的值,也可以是推定的值。这种思想方法是一种在某种意义上可知的对策(博弈)观点。随着方差减少法的开发和大型超高速计算机的出现,它不仅是仿真诸方法中最重要的—种方法,而且也是系统工程诸方法中最有效的一种方法。
它的一类重要的所求解问题是可以转化为某种随机分布的特征数,比如随机事件出现的概率,或者随机变量的期望值。通过随机抽样的方法,以随机事件出现的频率估计其概率,或者以抽样的数字特征估算随机变量的数字特征,并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。
例题:用蒙特卡洛法求解y=x^2
思路:
在0-4之间生成随机数x,在0-16之间生成随机数y,根据公式y=x^2判断所生成的随机数是否在所求面积部分中。然后计算在所求面积中随机数的比例,乘以64即为所求面积。
操作过程:
生成1-1000的按顺序排列的数字(为了计算所求的比例);
生成随机数x:函数:RAND()*(4-0)+0;
生成随机数y:函数:=RAND()*(16-0)+0;
判断是否在所求面积中:y<x^2 是,反之否,函数:IF(A2^2>=B2,1,0);
计算积分:函数:64*(SUM(D2)/A2) (第一列的数字用来代表生成的总随机数的个数)。
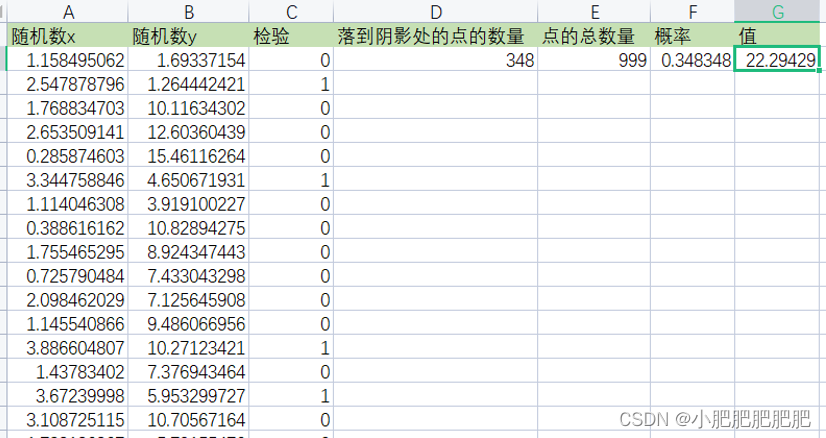
 使用蒙特卡洛法计算积分实例解析
使用蒙特卡洛法计算积分实例解析




 本文介绍了蒙特卡洛方法的基本原理及其在求解积分问题中的应用。通过一个具体的例子,展示了如何利用随机数生成和概率统计来估算函数y=x^2在0到4区间内的积分,通过计算满足条件的随机数比例乘以区域面积得到积分的近似值。
本文介绍了蒙特卡洛方法的基本原理及其在求解积分问题中的应用。通过一个具体的例子,展示了如何利用随机数生成和概率统计来估算函数y=x^2在0到4区间内的积分,通过计算满足条件的随机数比例乘以区域面积得到积分的近似值。
















 2402
2402

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








