线性回归算法中损失函数（误差函数/目标函数）的来历及推导

南山十一少

已于 2023-08-03 15:37:46 修改

阅读量664

点赞数

分类专栏：机器学习文章标签： python 回归开发语言机器学习

于 2023-07-23 15:29:09 首次发布

本文链接：https://blog.csdn.net/weixin_71894495/article/details/131867958

版权

机器学习专栏收录该内容

17 篇文章 2 订阅

订阅专栏

本文以线形回归为例，利用高斯分布概率密度函数和极大似然估计公式推导出线性回归误差函数通用表达式。

以一元线性回归算法为例，其模型如下所示：

$f(x) = \beta _{0} + \beta _{1}x + \varepsilon$ (1)

假如给定 i=14 个样本数据 $[xi, yi]$ ：

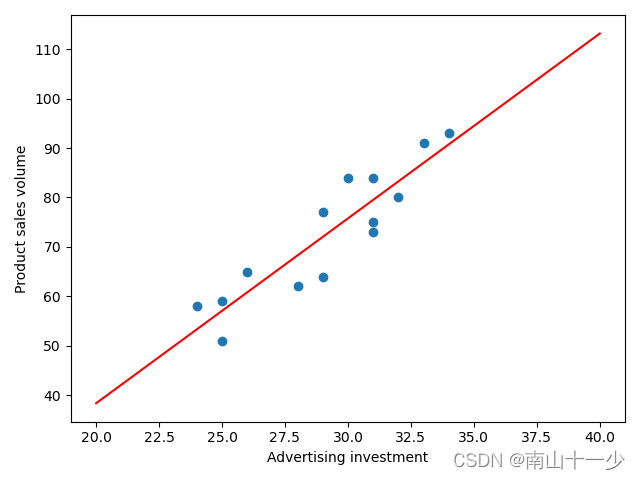
[ [29, 77], [28, 62], [34, 93], [31, 84], [25, 59], [29, 64], [32, 80], [31, 75], [24, 58], [33, 91], [25, 51], [31, 73], [26, 65], [30, 84]]

线性回归的原理即为通过确定模型参数，确定所有样本值代入模型后得到的结果值与真实值累计误差最小。以一元线性回归为例，直观的看如图所示，即为找到一条直线，穿过所有样本点，并使各个点到直线的累计距离 $\varepsilon$ 最小，从而求出直线方程的参数 $\beta _{0}$ 和参数 $\beta _{1}$ 的值。

如果是多元线性回归，即样本的特征向量不止一个维度，同样遵循以上模型特点和原理，更通用的线形回归表达方式如下：

$f(x) = \beta _{0} + \beta _{1}x_{1} + \beta _{2}x_{2} +... + \beta _{i}x_{i}+ \varepsilon$ (2)

以上表达式可通过向量的方式进行表达，如下所示：

$y^{(i)} = \beta ^{T}X^{(i)} + \varepsilon ^{(i)}$ (3)

因为误差具有随机性，符合独立同分布特点，高斯概率分布函数如下：

$f(x) = \frac{1}{\sigma\sqrt{2\pi }}exp(-\frac{(x-\mu )^{2}}{2\sigma ^{2}})$ (4)

因误差项满足高斯概率分布：

$\rho (\varepsilon ^{i}) = \frac{1}{\sigma\sqrt{2\pi }}exp(-\frac{(\varepsilon ^{(i)})^{2}}{2\sigma ^{2}})$ (5)

将误差代入高斯分布：

$\rho (y^{(i)}|X^{(i)};\beta ) = \frac{1}{\sigma\sqrt{2\pi }}exp(-\frac{(y^{(i)}-\beta ^{T}X^{(i)})^{2}}{2\sigma ^{2}})$ (6)

根据极大似然估计的原理，根据样本发生的概率估计整个事件的概率，其主要思想是所有样本发生的总概率最大的概率即为事件的概率，因为样本独立同分布，故所有样本概率积求最大值：

$L(\beta ) = \prod_{i=1}^{m}P(y^{(i)}|X^{(i)};\beta ) = \prod_{i=1}^{m}\frac{1}{ \sigma\sqrt{2\pi }}exp(-\frac{(y^{(i)}-\beta ^{T}X^{(i)})^{2}}{2\sigma ^{2}})$ (7)