泰勒公式的介绍、应用及常见题型

liquor.111

已于 2023-04-20 21:27:23 修改

阅读量8.5k

点赞数 6

分类专栏：高数文章标签：学习大数据

于 2023-01-18 20:21:23 首次发布

本文链接：https://blog.csdn.net/weixin_72845410/article/details/128667397

版权

高数专栏收录该内容

1 篇文章

订阅专栏

文章介绍了泰勒公式的基本概念，包括证明过程、余项的两种类型（佩亚诺型和拉格朗日型）以及麦克劳林公式。重点讲述了泰勒公式在解决常见数学问题中的应用，如展开函数、求极限、比较无穷小及证明等式和不等式，强调了正确选择和使用泰勒展开式的关键性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

目录

一、简介

1.泰勒公式及其证明过程

2.两种类型的余项

3.麦克劳林公式

二、泰勒公式常见题型

1.用泰勒公式展开函数

2.用泰勒公式求极限

3.用泰勒公式讨论无穷小的比较

4.用泰勒公式证明等式和不等式

一、简介

1.泰勒公式及其证明过程

泰勒中值定理1：若f(x)在含有 $x_{0}$ 的某个邻域内具有n阶倒数，则对于该邻域内任一点x,(x趋近于 $x_{0}$ )则有： $f(x)=f(x_{0})+\frac{f(x_{0}){}'}{1!}\cdot (x-x_{0})+\frac{f(x_{0}){}''}{2!}\cdot (x-x_{0})^{2}+......+\frac{f^{(n)}(x_{0})}{n!}\cdot (x-x_{0})^{n}+R_{n}(x)$

其中 $R_{n}(x)$ 为余项,根据需要选择使用佩亚诺型还是拉格朗日型，具体见后文（两种类型的余项）

证明：

$\because \Delta y\approx f(x){}'\Delta x,\therefore f(x)-f(x_{0})=f(x_{0}){}'(x-x_{0})$

$\therefore f(x)\approx f(x_{0})+f(x_{0}){}'(x-x_{0})$ 一次表达式

令 $f(x)=p_{n}(x)=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})^{2}+......+a_{n}(x-x_{0})^{n}$

当 $x=x_{0},a_{0}=f(x_{0})$ ;

$a_{1}=f(x_{0}){}'$ , $2!a_{2}=f(x_{0}){}''$ …… $n!a_{n}=f^{(n)}(x_{0})$ 先求导再代入 $x=x_{0}$

则 $a_{1}=f(x_{0})$ , $a_{2}=\frac{f(x_{0}){}''}{2!}$ …… $a_{n}=\frac{f^{(n)}(x_{0})}{n!}$ 即证。

2.两种类型的余项

1.佩亚诺型余项 $R_{n}=\circ ((x-x_{0})^{n})$ 取前一项的自变量 $(x-x_{0})^{n}$

若你所写的泰勒公式只有三项，则 $R_{n}=(x-x_{0})^{2}$ ,取四项则 $R_{n}=(x-x_{0})^{3}$ ，其他同理

2.拉格朗日型余项

泰勒中值定理2：若f(x)在含有 $x_{0}$ 的某个邻域内具有n+1阶导数，则对于该邻域内任一点x,(x趋近于 $x_{0}$ ),则有 $R_{n}=\frac{f^{(n+1)}(\xi )}{(n+1)!}(x-x_{0})^{n+1}$ ,此式子即为拉格朗日型余项

$\because n=0$ 时 $f(x)=f{}'(\xi )(x-x_{0})+f(x_{0})$ 即 $f{}'(\xi )=\frac{f(x)-f(x_{0})}{x-x_{0}}$ 为拉格朗日中值定理

3.麦克劳林公式

当泰勒公式中 $x_{0}=0$ 时即为麦克劳林公式： $f(x)=f(0)+\frac{f(0){}'}{1!}x+\frac{f(0){}''}{2!}x^{2}+......+\frac{f^{(n)}(0)}{n!} x^{n}+\frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1}$ $(0<\theta <1)$

注意：麦克劳林公式的使用条件：因为x趋近于 $x_{0}$ ，而此时 $x_{0}=0$ ，所以x也趋近于零

二、泰勒公式常见题型(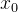 $x_{0}$ 的选取很关键)

1.用泰勒公式展开函数

方法：对原函数多求几次导，找到规律，写出有规律的式子
例子：求函数f(x)=lnx按(x-2)展开的带有佩亚诺型余项的n阶泰勒公式

解：令 $x_{0}=2$ , $f(2)=ln^{2}$ 对f(x)多次求导，又对 $ln^{x}$ 不断求导找出规律

$(ln^{x}){}'=\frac{1}{x}$ $(ln^{x}){}''=-\frac{1}{x^{2}}$ $(ln^{x}){}'''=\frac{2!}{x^{3}}$ ……

$\therefore f^{(n)}(x)=\frac{(-1)^{n-1}(n-1)!}{x^{n}}$ ,将x=2带入式子，然后写出泰勒展开式

$ln^{x}=f(2)+\frac{f(2){}'}{1!}\cdot (x-2)+\frac{f(2){}''}{2!}\cdot (x-2)^{2}+......+\frac{f^{(n)}(2)}{n!}\cdot (x-2)^{n}+\circ ((x-2)^{n})$

$=ln^{2}+\frac{1}{2^{1}}(x-2)-\frac{1}{2!\cdot 2^{2}}(x-2)^{2}+\frac{1}{3!\cdot 2^{3}}(x-2)^{3}......+\frac{(-1)^{n-1}(n-1)!}{n!\cdot 2^{n}}(x-2)^{n}+\circ ((x-2)^{n})$

$=ln^{2}+\frac{1}{2^{1}}(x-2)-\frac{1}{2!\cdot 2^{2}}(x-2)^{2}+\frac{1}{3!\cdot 2^{3}}(x-2)^{3}......+\frac{(-1)^{n-1}}{n\cdot 2^{n}}(x-2)^{n}+\circ ((x-2)^{n})$

2.用泰勒公式求极限

方法：1.先观察式子中有无可替换的等价无穷小

2.再观察分子分母中哪些式子需要用泰勒展开

3.展开时泰勒公式中 $x^{n}$ 与原式中本身次方最大的 $x^{m}$ 的关系为n<=m

4.注意可以转换的式子如 $(1+1/x)^{x}=e^{xln^{(1+1/x)}}$ ,再对 $ln(1+1/x)$ 用泰勒公式展开

5.展开时注意是否可以自变量整体代换如 $ln(1+1/x)$ ，我们知道常用的 $ln(1+x)$ 的泰勒展开式，可以直接用1/x替换x，前提是用来替换的式子必须趋近于零 $(x\rightarrow x_{0},x_{0}=0)$

例题1：求极限 $\lim_{x\rightarrow 0}\frac{cosx-e^-{\frac{x^{2}}{2}}}{x^{4}}$ (提示:对cosx泰勒展开，对 $e^-{\frac{x^{2}}{2}}$ ，由常见 $e^{x}$ 泰勒展开，用 $-{\frac{x^{2}}{2}}$ 整体代换 $e^{x}$ 展开式中的x，两项展开式中x最大次方应该 <=4，最后答案为 $-\frac{1}{12}$ )
例题2：求极限 $\lim_{x\rightarrow 0}\frac{xln^{(1+x)}}{e^{x}-x-1}$ (提示：使用等价无穷小的替换，再对 $e^{x}$ 用泰勒展开，最后答案为2）
例题3：求极限 $\lim_{x\rightarrow +\infty }{\frac{e}{2}}x+x^{2}[ (1+\frac{1}{x})^{x}-e]$

解：由泰勒公式 $(1+\frac{1}{x})^{x}=e^{xln^{(1+\frac{1}{x})}}=e^{x[\frac{1}{x}-{\frac{1}{2x^{2}}}+\frac{1}{3x^{3}}+\circ (\frac{1}{x^{3}})]}=e^{1-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})}$ 对转换后的式子提出一个e，得到 $e\cdot e^{[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]}$ ，此时对 $e^{[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]}$ 用麦克劳林展开，将 $[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]$ 整体看做x代入 $e^{x}$ 的麦克劳林公式，后续步骤比较简单，这里不给出解答了，最后答案等于 $\frac{11}{24}e$

（为什么上一步展开到 $e^{1-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})}$ 时不能用整体代入而要先提一个e出来呢？，因为x趋近于无穷，原来的次方 ${1-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})}$ 是趋近于1的，而不符合麦克劳林的展开条件x趋近于0，当提出e时，后式就可以直接整体代入，用麦克劳林公式展开）

3.用泰勒公式讨论无穷小的比较

方法：统一单位，赋值
例题：设 $x\rightarrow 0$ 时， $e^{x}-(ax^{2}+bx+1)$ 是比 $x^{2}$ 高阶的无穷小，求a和b的值（提示：由题 $\frac{e^{x}-(ax^{2}+bx+1)}{x^{2}}=0$ ,对 $e^{x}$ 泰勒展开至式子中出现 $x^{2}$ ，再对分母合并同类项，整体等于0，即可求出a、b）

4.用泰勒公式证明等式和不等式（重难点）

方法：注意 $x_{0}$ 的选取

1.若只需要证明的结果中不含一阶导数时，可考虑选取题目已知的一阶导数的点或隐含为一阶导数已知的点

2.积分不等式还可考虑选取 $\frac{a+b}{2}$ ,因为 $\int_{b}^{a}f(x_{0})(x-\frac{a+b}{2})$ 积分后可把含 $f{}'(x_{0})$ 消去

例题1：试证明：若f(x)在[a,b]上存在二阶导数，且 $f{}'(a)=f{}'(b)=0$ ,则存在 $\xi \in (a,b)$ 使 $|f{}''(\xi )|>=\frac{4}{(b-a)^{2}}|f(a)-f(b)|$ (想办法用给出的条件构造该函数，选取题目已知的一阶导数的点a，b为分别为 $x_{0}$ )