FM接收机及正交鉴频器设计

FM接收机及正交鉴频器设计

设计一个单信道超外差结构的 FM 接收机，使用Multisim验证频点和带宽是否满足需求。

功能需求如下：

• 接收机接收到的已调信号工作频点为 30MHz，最大频偏为 15KHz，调制指数为3，最大振幅为100的调频信号。下混频器可以将已调信号搬移至10.7MHz 的中频频点。解调器输入的中频信号振幅至少为 100mV。
  请用数学方法描述接收机的工作过程，并测量接收机中频输出的频点和带宽，
  与理论计算结果进行比较。
• 为发射机设计正交鉴频器（包括后级低频放大器和滤波器），实现对调频信号
  的无失真鉴频输出。要求如下：
  （1）设计连续移相网络，将输入调频信号的频率变化转换为相位变化。
  （2）设计乘积型鉴相器，检测相位变化。可以使用虚拟器件和集成电路模块。
  （3）指标要求：鉴频曲线中心点位于调频载波频率上，上下峰值点基本对称，
  线性范围大于 100KHz。
  （4）测试用调频波：载频10.7MHz，幅度有效值为100mV，调制信号频率为1KHz，频偏 10KHz。可以使用调频信号发生器作为测试输入。

1 单信道超外差式FM接收机设计及仿真验证

1.1 FM超外差式接收机结构框图

FM超外差式接收机结构框图如图1-1所示：

图 1-1 FM超外差式接收机结构框图

1.2 FM超外差式接收机数学描述分析

FM调频波的表达式为：

$$v(t)=V_{cm}\cos \left({\omega }_{c}t+m_f\sin \Omega t\right)$$

其中，$$m_f=\frac{\Delta {\omega }_m}{\Omega }=\frac{\Delta f_m}{F}$$，F为调制信号频率，$\Delta f_m$为最大频偏。

题意要求接收机收到的已调信号为：工作频点${\omega }_c=30MHz$，最大频偏$\Delta f_m=15kHz$，调制指数为$m_f=3$，最大振幅为$V_{cm}=100\mu V$的调频信号。

于是，调制信号的频率为5kHz，调频波的带宽为：

$$B{W}_{CR}=2\left(\Delta f_m+F\right)=2\times (15kHz+5kHz)=40kHz$$

下混频器可以将已调信号搬移至10.7MHz 的中频频点。混频器的本振信号表达式为：

$$V_{LO}(t)=V_{LO}cos{\omega }_{LO}t$$

则本振信号频率为：

$${\omega }_{LO}=30MHz-10.7MHz=19.3MHz$$

下混频器输出电压表达式为：

$$V_1(t)=V_{cm}\cos \left({\omega }_{c}t+m_f\sin \Omega t\right)\times V_{LO}\cos {\omega }_{LO}t$$

于是，下混频器输出电压包含的频率分量主要集中在10.7MHz与49.3MHz的频点处。因此使用带通滤波器滤出10.7MHz频点处的中频信号即可。

1.3 仿真设计与验证

中频信号的滤波器采用最大平坦带通滤波器进行设计，原理图如图2-2所示。

图 1-2最大平坦带通滤波器原理图

使用在线软件进行设计，滤波器阶数设为4阶，中心频率为10.7MHz，带宽为1MHz，输出阻抗为50Ω
微波射频网——最大平坦带通滤波器计算器

图 1-3最大平坦带通滤波器设计

下混频器使用Multisim虚拟模拟乘法器实现，增益为1V/V，得到下混频器及中频带通滤波器电路图如图1-4所示。

图1-4下混频器及中频滤波器电路原理图

由于题目要求，解调器输入的中频信号振幅至少为100mV，而FM输入信号振幅仅为100$\mu V$，因此在带通滤波器后级接入五级同相比例放大器，对中频信号进行线性放大。

图1-5 中频放大器设计

测量中频输出电压波形、振幅、频点及带宽。

输出波形图如图1-6所示，符合FM调频信号的特征。

图 1-6中频点输出波形图

输出电压有效值约为186mV大于100mV，符合题意要求，且输出电压频率为10.7MHz，在中频频点处。

图 1-7输出电压探针数据测量

使用频率计数器对中频输出电压频率进行测量，得到频率摆动范围为$10.685MHz\sim 10.715MHz$，符合$\Delta f_m=15kHz$的最大频偏理论值。

图 1-8 输出电压频偏测量

使用频谱分析仪测量中频输出信号的频谱，带宽约为41kHz，与理论计算值近似。

图 1-9输出电压频谱测量

2 正交鉴频器设计

2.1 移相网络设计

FM接收机的解调器部分由正交鉴频器构成，正交鉴频器由频相转换网络与乘积型鉴相器组成，将输入调频波的频率变化转换为输出信号的一个附加相移，并用鉴相器转换为输出信号电压的变化，其原理图如图2-1所示。

图 2-1正交鉴频器原理图

对于移相网络的参数估算，根据

$$\Delta \phi =-arctg\xi =-arctg2Q_e\frac{\Delta \omega (t)}{{\omega }_c}$$

确定能确保移相网络为线性相移的回路Q值。

线性相移要求：

$$|\Delta \phi |<\frac{\pi }{6}$$

即
$$\xi <tg\frac{\pi }{6}=0.577$$

于是，确保不失真解调的Q值为：

$$Q_e<0.577\frac{f_c}{2\Delta f_m}=0.577\times \frac{10.7MHz}{2\times 15kHz}=205.797$$

取$$Q_e=200$$，移相网络中$R_p$一般取$20k\Omega \sim 60k\Omega$，$C_1$一般取$5\sim 10pF$。

$${\omega }_0=2\pi \times 10.7MHz$$，取$R_p=20k\Omega$，$C_1=10pF$，根据

$$Q_e=\frac{R_P}{{\omega }_{0}L}$$

则电感$L=1.4874\mu F$。

根据

$${\omega }_0=\frac{1}{\sqrt{L(C_1+C)}}={\omega }_c$$

于是电容$C=138.786\mu F$。

得到移相网络电路图如图2-2所示。

图 2-2移相网络电路原理图

理论移相网络幅频特性曲线与相频特性曲线如图2-3所示，在${\omega }_0$处输入信号V1与输入信号V2正交，${\phi }_A=\frac{\pi }{2}$，相位差与频偏成正比。

图 2-3移相网络幅频特性曲线与相频特性曲线

对电压探针2进行交流扫频分析，得到幅频特性曲线与相频特性曲线如图2-4所示。在10.7MHz附近$${\phi }_A=\frac{\pi }{2}$$，实际曲线特征与理论曲线特征相符。说明移相网络设计满足题意要求。

图 2-4移相网络幅频特性曲线与相频特性曲线

2.2 乘积型鉴相器设计

乘积型鉴相器由模拟乘法器和低通滤波器组成，首先使用虚拟模拟乘法器进行设计。

低通滤波器电阻R取3k$\Omega$，C取0.01$\mu F$，则低通滤波器的上限截至频率为：

$$f_0=\frac{1}{2\pi RC}=5350Hz$$

正交鉴频器整体电路图如图2-5所示。

图 2-5正交鉴频器仿真电路原理图

当输入测试调频波信号：载频10.7MHz，幅度有效值为100mV，调制信号频率为1KHz，频偏10KHz时，正交鉴频器输出波形图如图2-6所示。

测得解调所得信号的频率约为$$f=\frac{1}{996.483\mu s}=1003.52Hz$$，与调制信号频率1000Hz接近，误差较小，符合题意要求。

图 2-6正交鉴频器输出波形图

2.3 正交鉴频器指标验证

由于Multisim虚拟模拟乘法器不能进行AC扫频交流分析，因此需采用集成电路进行设计，验证正交鉴频曲线。

模拟乘法器使用AD834，其为ANALOG DEVICES的一款500 MHz四象限乘法器。

AD834集成电路内部原理图如图2-7所示。

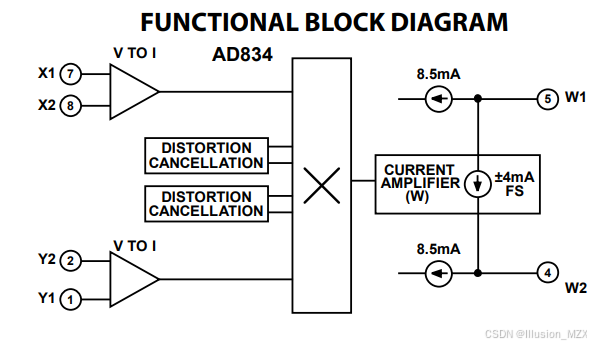
图 2-7 AD834模拟乘法器原理图

参考AD官方 MT-079模拟乘法器设计指南中的AD834的基本连接进行设计。

图 2-8 AD834参考设计

从AD官方的AD834数据手册及产品说明处下载AD834spice仿真模型并导入Multisim进行仿真设计与验证。

得到仿真电路原理图如图2-9所示。

图 2-9基于AD834设计正交鉴频器

使用AC交流分析，对电压探针3进行9MHz~13MHz扫频，得到输出幅频特性曲线与相频特性曲线如图2-10所示。

图 2-10正交鉴频幅频特性与相频特性曲线

鉴频曲线为S型，与理论鉴频曲线相符，其中鉴频曲线中心点位于调频载波频率10.7MHz上，且上下峰值点基本对称。

图 2-11理论鉴频曲线

测得线性鉴频范围$2\Delta f_m\approx 400kHz>100kHz$。