主成分分析
在实际问题中,我们经常会遇到研究多个变量的问题,而且在多数情况下,多个变量之间常常存在一定的相关性。由于变量个数较多再加上变量之间的相关性,势必增加了分析问题的复杂性。如何从多个变量中综合为少数几个代表性变量,既能够代表原始变量的绝大多数信息,又互不相关,并且在新的综合变量基础上,可以进一步的统计分析,这时就需要进行主成分分析。
第一节 主成分分析的原理及模型
一、主成分分析的基本思想与数学模型
(一)主成分分析的基本思想
主成分分析是采取一种数学降维的方法,找出几个综合变量来代替原来众多的变量,使这些综合变量能尽可能地代表原来变量的信息量,而且彼此之间互不相关。这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。
主成分分析所要做的就是设法将原来众多具有一定相关性的变量,重新组合为一组新的相互无关的综合变量来代替原来变量。通常,数学上的处理方法就是将原来的变量做线性组合,作为新的综合变量,但是这种组合如果不加以限制,则可以有很多,应该如何选择呢?如果将选取的第一个线性组合即第一个综合变量记为F1,自然希望它尽可能多地反映原来变量的信息, 这里 “信息”用方差Var(F1)来测量,即希望 越大 ,表示F1包含的 信息越多 。因此在 所有的线性组合中所选取的 应该是方差最大的,故称为第一主成分。如果第一主成分 不足以代表原来 个变量的信息,再考虑 选取 即第二个线性组合F2,为了有效地反映原来信息,已有的信息就不需要再出现在中,用数学语言表达就是要求,称为第二主成分, 依此类推 可以构造出第三、四……第P个主成分。(二)主成分分析的数学模型
对于一个样本资料,观测p个变量X1,X2.......Xp,n个样品的数据资料阵为:
主成分分析就是将P个观测变量综合成为P个新的变量(综合变量),即
简写为:
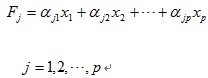
要求模型满足以下条件:

于是,称为第一主成分F1,为第二主成分F2,依此类推,有p第个主成分。主成分又叫主分量。这里我们称a(ij)为主成分系数。
二、主成分分析的几何解释
假设有n个样品,每个样品有二个变量,即在二维空间中讨论主成分的几何意义。设n个样品在二维空间中的分布大致为一个椭园,如下图所示:


经过旋转变换后,得到下图的新坐标:
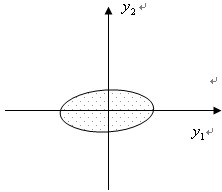
(1)n个点的坐标y1和y2的相关几乎为零。
(2)二维平面上的n个点的方差大部分都归结为y1轴上,而y2轴上的方差较小。
y1和y2称为原始变量x1和x2的综合变量。由于n个点在y1轴上的方差最大,因而将二维空间的点用在y1轴上的一维综合变量来代替,所损失的信息量最小,由此称轴y1为第一主成分,y1轴与y2轴正交,有较小的方差,称它为第二主成分。
三、主成分分析的应用
主成分概念首先是由Karl parson 在1901年引进,但当时只对非随机变量来讨论的。1933年Hotelling将这个概念推广到随机变量。特别是近年来,随着计算机软件的应用,使得主成分分析的应用也越来越广泛。
其中,主成分分析可以用于系统评估。系统评估是指对系统营运状态做出评估,而评估一个系统的营运状态往往需要综合考察许多营运变量,例如对某一类企业的经济效益作评估,影响经济效益的变量很多,很难直接比较其优劣,所以解决评估问题的焦点是希望客观、科学地将一个多变量问题综合成一个单变量形式,也就是说只有在一维空间中才能使排序评估成为可能,这正符合主成分分析的基本思想。在经济统计研究中,除了经济效益的综合评价研究外,对不同地区经济发展水平的评价研究,不同地区经济发展竞争力的评价研究,人民生活水平、生活质量的评价研究,等等都可以用主成分分析方法进行研究。
另外,主成分分析除了用于系统评估研究领域外,还可以与回归分析结合,进行主成分回归分析,以及利用主成分分析进行挑选变量,选择变量子集合的研究。
第二节 主成分的导出及主成分分析的步骤
一、主成分的导出
根据主成分分析的数学模型的定义,要进行主成分分析,就需要根据原始数据,以及模型的三个条件的要求,如何求出主成分系数,以便得到主成分模型。这就是导出主成分所要解决的问题。
1、根据主成分数学模型的条件要求主成分之间互不相关,为此主成分之间的协差阵应该是一个对角阵。即,对于主成分,
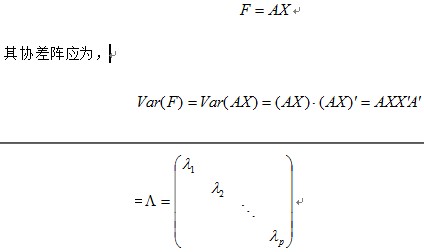
3、再由主成分数学模型条件和正交矩阵的性质,若能够满足条件,最好要求为正交矩阵,即满足:
AA'=I
于是,将原始数据的协方差代入主成分的协差阵公式得

展开等式两边,根据矩阵相等的性质,这里只根据第一列得出的方程为:

为了得到该齐次方程的解,要求其系数矩阵行列式为0,即


二、主成分分析的计算步骤
样本观测数据矩阵为:
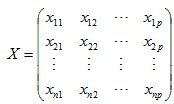
第一步:对原始数据进行标准化处理。

第二步:计算样本相关系数矩阵。

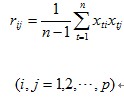
第三步:用雅克比方法求相关系数矩阵的特征值和相应的特征向量。
第四步:选择重要的主成分,并写出主成分表达式。
主成分分析可以得到个主成分,但是,由于各个主成分的方差是递减的,包含的信息量也是递减的,所以实际分析时,一般不是选取个主成分,而是根据各个主成分累计贡献率的大小选取前个主成分,这里贡献率就是指某个主成分的方差占全部方差的比重,实际也就是某个特征值占全部特征值合计的比重。
贡献率越大,说明该主成分所包含的原始变量的信息越强。主成分个数的选取,主要根据主成分的累积贡献率来决定,即一般要求累计贡献率达到85%以上,这样才能保证综合变量能包括原始变量的绝大多数信息。
另外,在实际应用中,选择了重要的主成分后,还要注意主成分实际含义解释。主成分分析中一个很关键的问题是如何给主成分赋予新的意义,给出合理的解释。一般而言,这个解释是根据主成分表达式的系数结合定性分析来进行的。主成分是原来变量的线性组合,在这个线性组合中个变量的系数有大有小,有正有负,有的大小相当,因而不能简单地认为这个主成分是某个原变量的属性的作用,线性组合中各变量系数的绝对值大者表明该主成分主要综合了绝对值大的变量,有几个变量系数大小相当时,应认为这一主成分是这几个变量的总和,这几个变量综合在一起应赋予怎样的实际意义,这要结合具体实际问题和专业,给出恰当的解释,进而才能达到深刻分析的目的。
由于时间过长的原因,上面的参考文献我忘记了,貌似是来自百度文库的文章;后记补充
参考文献:http://wenku.baidu.com/view/fdc4f73d43323968011c923a.html
相关系数定义与说明
相关系数,或称线性相关系数、皮氏积矩相关系数(Pearson product-momentcorrelation coefficient, PPCC)等,是衡量两个随机变量之间线性相关程度的指标。它由卡尔·皮尔森(Karl Pearson)在1880年代提出,现已广泛地应用于科学的各个领域。
相关系数计算公式
相关系数(r)的定义如右图所示,取值范围为[-1,1],r>0表示正相关,r<0表示负相关,|r|表示了变量之间相关程度的高低。特殊地,r=1称为完全正相关,r=-1称为完全负相关,r=0称为不相关。通常|r|大于0.8时,认为两个变量有很强的线性相关性。[2]
样本相关系数常用r表示,而总体相关系数常用ρ表示。
相关性质
(1)对称性:X与Y的相关系数(rXY)和Y与X之间的相关系数(rYX)相等;
(2)相关系数与原点和尺度无关;
(3)若X与Y统计上独立,则它们之间的相关系数为零;但r=0不等于说两个变量是独立的。即零相关并不一定意味着独立性;
(4)相关系数是线性关联或线性相依的一个度量,它不能用于描述非线性关系;
(5)相关系数只是两个变量之间线性关联的一个度量,不一定有因果关系的含义
协方差矩阵
参考文献:http://hi.baidu.com/hehui1500/item/fba9444327a24693823ae1e9
统计学的基本概念
学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合X1到Xn,依次给出这些概念的公式描述,这些高中学过数学的孩子都应该知道吧,一带而过。
很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
为什么需要协方差?
上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的优秀 程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~ 协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越优秀就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质,如:
协方差多了就是协方差矩阵
上一节提到的优秀和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算多个协方差,那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义:
这个定义还是很容易理解的,我们可以举一个简单的三维(x,y,z)的例子,假设数据集有三个维度,则协方差矩阵为
可见,协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间,拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度,心中明确这个整个计算过程就会顺流而下,这么一来就不会迷茫了
总结
原始数据X,计算相关系数矩阵S(是个对称方阵),然后求S的特征值和特征向量,之后把个特征向量按照列排放,组成系数矩阵U。然后依据最少丢失信息的原则,选择K个旋转后的变量F,完成主成分分析。






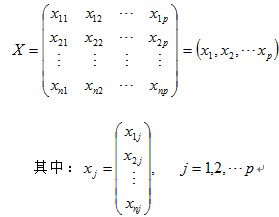
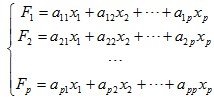

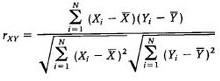


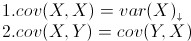

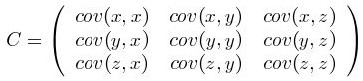













 2936
2936











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








