GCN(Graph Convolutional Network)
Paper : Semi-Supervised Classification With Graph Convolutional Networks
图卷积神经网络
本部分旨在将卷积运算推广到图领域,这一方向的研究成果一般被分为两类:基于谱分解的方法和基于空间结构的方法
基于谱分解的方法
Spectral Network
SpecNet
g θ ⋆ x = U g θ ( Λ ) U T x \bm{ g_θ \star x = Ug_θ(Λ)U^Tx } gθ⋆x=Ugθ(Λ)UTx
其中 x x x为所有节点组成的向量(一个节点代表 x x x中的一个标量), g θ = d i a g ( θ ) g_θ = diag(θ) gθ=diag(θ)为卷积核, U U U是归一化拉普拉斯矩阵的特征向量组成的矩阵, D 、 A 和 Λ D、A和Λ D、A和Λ分别为度矩阵、邻接矩阵和特征值的对角矩阵
- 这一卷积运算会导致潜在的密集计算,并且导致卷积核不满足局部性(聚合的节点与实际的空间结构不对应)
ChebNet
ChebNet
g θ ⋆ x = ∑ k = 0 K θ k T k ( L ~ ) x \bm{ g_θ \star x = \sum\limits_{k=0}^{K}{θ_kT_k(\tilde{L})x} } gθ⋆x=k=0∑KθkTk(L~)x
GCN
GCN
g θ ⋆ x ≈ θ ( I N + D − 1 2 A D − 1 2 ) x \bm{ g_θ \star x ≈ θ(I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x } gθ⋆x≈θ(IN+D−21AD−21)x
-
N个节点,每个节点都有自己的特征向量,假设每个特征向量size为D,这些节点的特征组成一个NxD的矩阵X,各节点之间的连接关系(邻接矩阵)组成一个NxN的矩阵A,X和A就是GCN的输入
-
GCN是一个NN层,层与层之间的传播方式为H(l+1)=σ( D ~ \tilde{D} D~- 1 2 \frac{1}{2} 21 A ~ \tilde{A} A~ D ~ \tilde{D} D~- 1 2 \frac{1}{2} 21H(l)W(l))
-
A ~ \tilde{A} A~=A+I,I为单位矩阵。这里加上单位矩阵I是为了使邻接矩阵A对角线上的元素变为1。若对角元素为0的话,和特征矩阵H相乘时,只会计算一个node的所有邻居的特征的加权和,该node本身的特征却被忽略了。(重归一化,renormalization)
-
D ~ \tilde{D} D~是 A ~ \tilde{A} A~的度矩阵
-
D ~ \tilde{D} D~- 1 2 \frac{1}{2} 21 A ~ \tilde{A} A~ D ~ \tilde{D} D~- 1 2 \frac{1}{2} 21这一部分主要作用是对A对称归一化处理。未经归一化的矩阵与其他特征矩阵相乘会改变特征原本的分布,产生一些不可预测的影响
-
H是每一层的特征,对于输入层来说H=X
-
W是可学习的权重参数
-
σ是非线性激活函数
AGCN(Adaptive GCN)
AGCN
-
前述模型均使用原始图结构表示节点之间的关系,然而不同节点之间可能存在隐式关系,于是提出AGCN以自适应学习隐式关系
-
AGCN会学习“残差”图拉普拉斯矩阵 L r e s L_{res} Lres并作如下变换:
L ^ = L + α L r e s \bm{ \hat{L} = L + αL_{res} } L^=L+αLres
- α为超参数, L r e s L_{res} Lres是通过一个学习得到的图邻接矩阵 A ^ \hat{A} A^计算出来的:
L r e s = I − D ^ − 1 2 A ^ D ^ − 1 2 \bm{ L_{res} = I - \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}} } Lres=I−D^−21A^D^−21
D ^ = d e g r e e ( A ^ ) \bm{ \hat{D} = degree(\hat{A}) } D^=degree(A^)
- A ^ \hat{A} A^是通过一个学习获得的度量指标计算得来的(欧几里得距离在图结构数据中已不适用,这里采用广义马哈拉诺比斯距离计算节点距离)
D ( x i , x j ) = ( x i − x j ) T M ( x i − x j ) \bm{ D(x_i, x_j) = \sqrt{(x_i - x_j)^TM(x_i - x_j)} } D(xi,xj)=(xi−xj)TM(xi−xj)
- M M M是一个通过学习得到的矩阵。AGCN计算高斯核G,并将G归一化,以获得密集邻接矩阵 A ^ \hat{A} A^
G x i , x j = e x p ( − D ( x i , x j ) / ( 2 σ 2 ) ) \bm{ G_{x_i, x_j} = exp(-D(x_i, x_j)/(2σ^2)) } Gxi,xj=exp(−D(xi,xj)/(2σ2))
基于空间结构的方法
上述介绍的基于谱分解的方法,其卷积核依赖于拉普拉斯特征基向量,而基向量取决于图的结构。这意味着针对特定结构训练的模型不能直接应用于具有不同结构的图,即模型的泛化性较差
基于空间结构的方法直接在图上定义卷积运算,从而针对在空间上相邻的领域进行运算。
Neural FP
Neural FP
- 针对不同度的节点使用不同的权重矩阵:
x = h v t − 1 + ∑ i = 1 ∣ N v ∣ h i t − 1 \bm{ x = h_v^{t-1} + \sum\limits_{i=1}^{|N_v|}{h_i^{t-1}} } x=hvt−1+i=1∑∣Nv∣hit−1
h v t = σ ( x W t ∣ N v ∣ ) \bm{ h_v^t = σ(xW_t^{|N_v|}) } hvt=σ(xWt∣Nv∣)
-
Neural FP首先将相邻节点连同本身的嵌入表示累加,然后使用一个权重矩阵进行学习
-
缺陷:针对不同度的节点都需要有一个权重矩阵,在某些极端情况下,参数量较大
PATCHY-SAN
PATCHY-SAN
-
这一模型首先为一些节点选择k个相邻节点并归一化,然后将这些经过归一化的相邻节点作为感受野进行卷积运算,步骤如下:
-
选择节点序列
- 模型并不会处理图中所有的节点,而会先通过节点标注来获得节点的顺序,然后使用s大小的步长在序列中选择节点,直到选中w个节点为止
-
选择相邻节点
- 这一步使用上一步选中的节点构造感受野。对每一个选中的节点进行BFS,以选取k个相邻节点:首先选取1跳距离的相邻节点,然后再考虑更远的节点,直到选取的相邻节点数达到k为止
-
图归一化
- 这一步旨在为感受野中的节点排序,以便从无序的图空间映射到矢量空间。这是最重要的步骤,其思想是为不同的图中的两个具有相似结构地位的节点分配相似的相对位置
-
应用卷积架构
- 在归一化后,使用CNN进行卷积。经过归一化的领域用作感受野,节点和边的属性被视为通道
-
-
该方法将非欧几里得数据转换成了欧几里得结构数据进行卷积处理
DCNN(Diffusion-convolutional Neural Network)
DCNN
H = σ ( W c ⊙ P ∗ X ) \bm{ H = σ(W^c⊙P^*X) } H=σ(Wc⊙P∗X)
其中, X X X为输入特征, P ∗ = P , P 2 , . . . , P K P^* = {P, P^2, ..., P^K} P∗=P,P2,...,PK, P P P为图邻接矩阵A按度归一化的转移矩阵
DGCN(Dual Graph Convolutional Network)
Paper : Dual Graph Convolutional Networks for Graph-Based Semi-Supervised Classification
DGCN
-
同时考虑图的局部一致性和全局一致性,使用两个卷积网络来捕获局部一致性和全局一致性
-
局部一致性
Z = D ~ − 1 2 A ~ D ~ − 1 2 X Θ \bm{ Z = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}XΘ } Z=D~−21A~D~−21XΘ
-
全局一致性:使用正向点互信息矩阵(Positive Pointwise mutual information matrix,PPMI)替换邻接矩阵
H ′ = σ ( D P − 1 2 X P D P − 1 2 H Θ ) \bm{ H^{'} = σ(D_P^{-\frac{1}{2}}X_PD_P^{-\frac{1}{2}}HΘ) } H′=σ(DP−21XPDP−21HΘ)
其中, X P X_P XP是PPMI矩阵, D P D_P DP是 X P X_P XP的对角度矩阵,σ是非线性激活函数 -
损失函数:
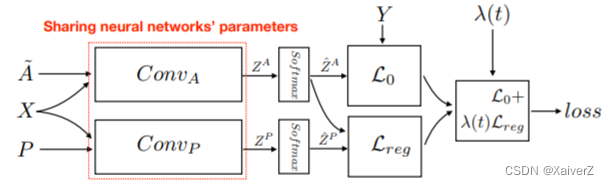
L = L 0 ( C o n v A ) + λ ( t ) L r e g ( C o n v A , C o n v P ) \bm{ L = L_0(Conv_A) + λ(t)L_{reg}(Conv_A, Conv_P) } L=L0(ConvA)+λ(t)Lreg(ConvA,ConvP)
λ ( t ) λ(t) λ(t)调节两部分损失的权重, L 0 ( C o n v A ) L_0(Conv_A) L0(ConvA)是结合节点标签的监督损失函数(交叉熵), L r e g ( C o n v A , C o n v P ) L_{reg}(Conv_A, Conv_P) Lreg(ConvA,ConvP)是两种卷积输出的MSE无监督回归损失
LGCN(Learnable Graph Convolutional Network)
Paper : Large-Scale Learnable Graph Convolutional Networks
LGCN
H ^ t = g ( H t , A , k ) \bm{ \hat{H}_t = g(H_t, A, k) } H^t=g(Ht,A,k)
H t + 1 = c ( H ^ t ) \bm{ H_{t+1} = c(\hat{H}_t) } Ht+1=c(H^t)
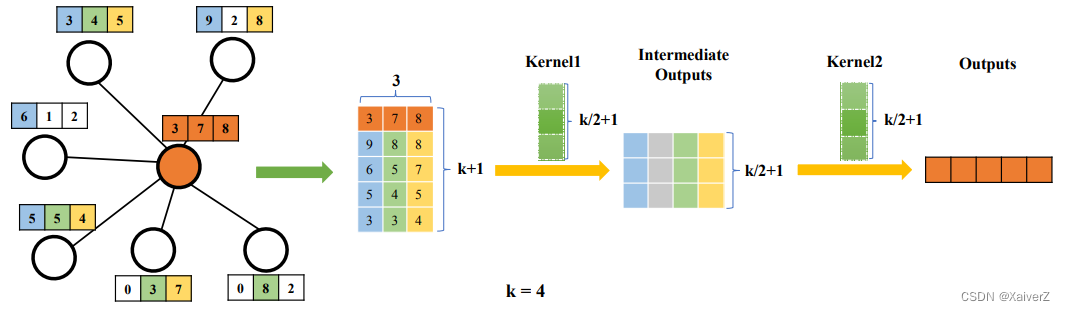
- 该模型使用对前 k k k个最大的节点值的选取操作来收集每个节点的信息。对于给定的节点,首先收集其相邻节点的特征。假设它有 n n n个相邻节点,并且每个节点具有 c c c维特征,则获得矩阵 M M M。如果 n < k n<k n<k,则用零列填充 M M M。然后,选择每一维最大的 k k k个节点值,也就是将每一列中的值排序并选择前 k k k个值。之后,将自身节点的嵌入表示插入 M M M 的第一行,得到矩阵 M ^ \hat{M} M^
MoNet
MoNet
-
空间域模型MoNet能泛化前述的数个模型。GCNN、ACNN、GCN、DCNN等均可被视为MoNet的特例
-
用x表示节点,并用y表示与该节点相邻的一个节点。MoNet对节点及其相邻节点计算伪坐标u(x, y),并对这些伪坐标设计权重函数:
D j ( x ) f = ∑ y ∈ N x w j ( u ( x , y ) ) f ( y ) \bm{ D_j(x)f = \sum\limits_{y∈N_x}{w_j(u(x, y))f(y)} } Dj(x)f=y∈Nx∑wj(u(x,y))f(y)
其中,模型需要学习的参数为 w Θ ( u ) = ( w 1 ( u ) , . . . , w J ( u ) ) w_Θ(u) = (w_1(u), ..., w_J(u)) wΘ(u)=(w1(u),...,wJ(u)), J J J表示选取的领域大小。接着就可以定义非欧几里得数据域的卷积的空间泛化形式:
( f ⋆ g ) ( x ) = ∑ j = 1 J g j D j ( x ) f \bm{ (f \star g)(x) = \sum\limits_{j=1}^J{g_jD_j(x)f} } (f⋆g)(x)=j=1∑JgjDj(x)f -
前述方法可以看作这种形式,只不过它们的 u u u和 w ( u ) w(u) w(u)有所区别
GraphSAGE
Paper : Inductive Representation Learning on Large Graphs
GraphSAGE
- GraphSAGE是一个通用的归纳推理框架,它通过采样和聚合相邻节点的特征来生成节点的嵌入表示。GraphSAGE模型的传播过程为:
h N v t = A G G R E G A T E t ( h u t − 1 , ∀ u ∈ N v ) \bm{ h_{N_v}^t = AGGREGATE_t({h^{t-1}_u, \forall u \in N_v}) } hNvt=AGGREGATEt(hut−1,∀u∈Nv)
h v t = σ ( W t ⋅ [ h v t − 1 ∣ ∣ h N v t ] ) \bm{ h_v^t = σ(W^t · [h_v^{t-1} || h_{N_v}^t]) } hvt=σ(Wt⋅[hvt−1∣∣hNvt])
-
GraphSAGE并不使用所有的相邻节点,而是均匀采样固定数量的相邻节点。以下是3种聚合函数AGGREGATE的具体实现:
-
均值聚合器(Mean Aggregator)
h v t = σ ( W ⋅ M E A N ( { h v t − 1 } ∪ { h u t − 1 , ∀ u ∈ N v } ) ) \bm{ h_v^t = σ(W · MEAN(\{h_v^{t-1}\} ∪ \{h_u^{t-1}, \forall u \in N_v\})) } hvt=σ(W⋅MEAN({hvt−1}∪{hut−1,∀u∈Nv}))
-
LSTM聚合器(LSTM Aggregator)
- 这里LSTM作用在打乱节点顺序的无序邻接节点集合上
-
池化聚合器(Pooling Aggregator)
- 将相邻节点的隐状态输入一个全连接层并进行最大池化(这里的最大池化运算可以用任意对称函数替代)
h N v t = m a x ( { σ ( W p o o l h u t − 1 + b ) , ∀ u ∈ N v } ) \bm{ h_{N_v}^t = max(\{σ(W_{pool}h_u^{t-1} + b), \forall u \in N_v\}) } hNvt=max({σ(Wpoolhut−1+b),∀u∈Nv})
-
-
损失函数
-
无监督
J G ( z u ) = − l o g ( σ ( z u T z v ) ) − Q ⋅ E v n ∼ P n ( v ) l o g ( σ ( − z u T z v n ) ) \bm{ J_G(z_u) = -log(σ(z_u^Tz_v)) - Q · E_{v_n \sim P_n(v)}log(σ(-z_u^Tz_{v_n})) } JG(zu)=−log(σ(zuTzv))−Q⋅Evn∼Pn(v)log(σ(−zuTzvn))
-
监督:交叉熵
-





















 691
691











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








