Python 数学应用（一）

原文：zh.annas-archive.org/md5/123a7612a4e578f6816d36f968cfec22

译者：飞龙

协议：CC BY-NC-SA 4.0

第一章：前言

Python 是一种功能强大、灵活且易于学习的编程语言。它是许多专业人士、爱好者和科学家的首选编程语言。Python 的强大之处来自其庞大的软件包生态系统和友好的社区，以及其与编译扩展模块无缝通信的能力。这意味着 Python 非常适合解决各种问题，特别是数学问题。

数学通常与计算和方程联系在一起，但实际上，这些只是更大主题的很小部分。在其核心，数学是关于解决问题、以及逻辑、结构化方法的学科。一旦你探索了方程、计算、导数和积分之外，你会发现一个庞大而优雅的世界。

本书是使用 Python 解决数学问题的介绍。它介绍了一些来自数学的基本概念，以及如何使用 Python 来处理这些概念，并提供了解决数学问题的模板，涵盖了数学中大量主题的各种数学问题。前几章侧重于核心技能，如使用 NumPy 数组、绘图、微积分和概率。这些主题在整个数学中非常重要，并作为本书其余部分的基础。在剩下的章节中，我们讨论了更多实际的问题，涵盖了数据分析和统计、网络、回归和预测、优化和博弈论等主题。我们希望本书为解决数学问题提供了基础，并为您进一步探索数学世界提供了工具。

本书的读者

读者需要具备基本的 Python 知识。我们不假设读者具有任何数学知识，尽管熟悉一些基本数学概念的读者将更好地理解我们讨论的技术的背景和细节。

本书涵盖的内容

第一章，基本软件包、函数和概念，介绍了本书其余部分需要的一些基本工具和概念，包括用于数学编程的主要 Python 软件包 NumPy 和 SciPy。

第二章，使用 Matplotlib 进行数学绘图，介绍了使用 Matplotlib 进行绘图的基础知识，这在解决几乎所有数学问题时都很有用。

第三章，微积分和微分方程，介绍了微积分的主题，如微分和积分，以及一些更高级的主题，如常微分方程和偏微分方程。

第四章，处理随机性和概率，介绍了随机性和概率的基础知识，以及如何使用 Python 探索这些概念。

第五章，处理树和网络，介绍了使用 NetworkX 软件包在 Python 中处理树和网络（图）的内容。

第六章，处理数据和统计，介绍了使用 Python 处理、操作和分析数据的各种技术。

第七章，回归和预测，描述了使用 Statsmodels 软件包和 scikit-learn 预测未来值的各种建模技术。

第八章，几何问题，演示了使用 Shapely 软件包在 Python 中处理几何对象的各种技术。

第九章，寻找最优解，介绍了使用数学方法找到问题的最佳解的优化和博弈论。

第十章，杂项主题，涵盖了使用 Python 解决数学问题时可能遇到的各种情况。

充分利用本书

本书中唯一的要求是使用最新版本的 Python，至少 Python 3.6，但更高版本更好。一些读者可能更喜欢使用 Python 的 Anaconda 发行版，该发行版包含本书中所需的许多软件包和工具。如果是这种情况，您应该使用conda软件包管理器来安装这些软件包。Python 支持所有主要操作系统——Windows、macOS 和 Linux——以及许多平台。以下表格涵盖了在撰写本书时使用的主要库及其版本：

书中涵盖的软件/库	版本	章节
Python	3.6 或更高版本	所有
NumPy	1.18.3	所有
SciPy	1.4.1	所有
Matplotlib	3.2.1	所有
Pandas	1.0.3	6 - 10
Bokeh	2.1.0	6
Scikit-Learn	0.22.1	7
Dask	2.18.1	10
Apache Kafka	2.5.0	10

如果您使用本书的数字版本，我们建议您自己输入代码或通过 GitHub 存储库（下一节中提供链接）访问代码。这样做将有助于避免与复制和粘贴代码相关的任何潜在错误。

一些读者可能更喜欢在 Jupyter 笔记本中而不是在简单的 Python 文件中逐步完成本书中的代码示例。本书中有一两个地方可能需要重复绘图命令。这些地方在说明中有标记。

下载示例代码文件

您可以从www.packt.com的帐户中下载本书的示例代码文件。如果您在其他地方购买了本书，您可以访问www.packtpub.com/support并注册，以便文件直接通过电子邮件发送给您。

您可以按照以下步骤下载代码文件：

1. 登录或注册www.packt.com。

2. 选择支持选项卡。

3. 点击代码下载。

4. 在搜索框中输入书名，然后按照屏幕上的说明操作。

下载文件后，请确保使用最新版本的以下软件解压或提取文件夹：

• WinRAR/7-Zip for Windows

• Zipeg/iZip/UnRarX for Mac

• 7-Zip/PeaZip for Linux

本书的代码包也托管在 GitHub 上，网址为github.com/PacktPublishing/Applying-Math-with-Python。如果代码有更新，将在现有的 GitHub 存储库上进行更新。

我们还有来自我们丰富书籍和视频目录的其他代码包，可在github.com/PacktPublishing/上找到。去看看吧！

代码示例

本书的代码示例视频可以在bit.ly/2ZQcwIM上观看。

使用的约定

本书中使用了许多文本约定。

CodeInText：表示文本中的代码单词、数据库表名、文件夹名、文件名、文件扩展名、路径名、虚拟 URL、用户输入和 Twitter 句柄。这里有一个例子：“decimal包还提供了一个Context对象，它允许对Decimal对象的精度、显示和属性进行精细控制。”

代码块设置如下：

from decimal import getcontext
ctx = getcontext()
num = Decimal('1.1')
num**4  # Decimal('1.4641')
ctx.prec = 4 # set new precision
num**4  # Decimal('1.464')

当我们希望引起您对代码块的特定部分的注意时，相关行或项目将以粗体显示：

from numpy import linalg

A = np.array([[3, -2, 1], [1, 1, -2], [-3, -2, 1]])
b = np.array([7, -4, 1])

任何命令行输入或输出都是这样写的：

          python3.8 -m pip install numpy scipy

粗体：表示一个新术语、一个重要单词或屏幕上看到的单词。例如，菜单或对话框中的单词会以这种方式出现在文本中。这里有一个例子：“从管理面板中选择系统信息。”

警告或重要说明会以这种方式出现。提示和技巧会以这种方式出现。

章节

在本书中，您会经常看到几个标题（准备工作，如何做，它是如何工作的，还有更多，和另请参阅）。

为了清晰地说明如何完成食谱，使用以下各节：

准备工作

本节告诉您在食谱中可以期待什么，并描述如何设置任何所需的软件或初步设置。

如何做…

本节包含按照食谱所需的步骤。

它是如何工作的…

本节通常包括对前一节发生的事情的详细解释。

还有更多…

本节包含有关食谱的额外信息，以使您对食谱更加了解。

另请参阅

本节提供了其他有用信息的链接，以帮助制作食谱。

第二章：基本包、函数和概念

在开始任何实际配方之前，我们将使用本章来介绍几个核心数学概念和结构及其 Python 表示。特别是，我们将研究基本数值类型、基本数学函数（三角函数、指数函数和对数）以及矩阵。由于矩阵与线性方程组的解之间的联系，矩阵在大多数计算应用中都是基本的。我们将在本章中探讨其中一些应用，但矩阵将在整本书中发挥重要作用。

我们将按照以下顺序涵盖以下主要主题：

• Python 数值类型

• 基本数学函数

• NumPy 数组

• 矩阵

技术要求

在本章和本书的整个过程中，我们将使用 Python 3.8 版本，这是写作时最新的 Python 版本。本书中的大部分代码将适用于 Python 3.6 及更高版本。我们将在不同的地方使用 Python 3.6 引入的功能，包括 f-strings。这意味着您可能需要更改任何终端命令中出现的python3.8，以匹配您的 Python 版本。这可能是另一个版本的 Python，如python3.6或python3.7，或者更一般的命令，如python3或python。对于后者的命令，您需要使用以下命令检查 Python 的版本至少为 3.6：

          python --version

Python 具有内置的数值类型和基本的数学函数，足以满足只涉及小计算的小型应用。NumPy 包提供了高性能的数组类型和相关例程（包括对数组进行高效操作的基本数学函数）。这个包将在本章和本书的其余部分中使用。我们还将在本章的后续配方中使用 SciPy 包。这两个包都可以使用您喜欢的包管理器（如pip）进行安装：

          python3.8 -m pip install numpy scipy

按照惯例，我们将这些包导入为更短的别名。我们使用以下import语句将numpy导入为np，将scipy导入为sp：

import numpy as np
import scipy as sp

这些约定在这些包的官方文档中使用，以及许多使用这些包的教程和其他材料中使用。

本章的代码可以在 GitHub 存储库的Chapter 01文件夹中找到，网址为github.com/PacktPublishing/Applying-Math-with-Python/tree/master/Chapter%2001。

查看以下视频以查看代码实际操作：bit.ly/3g3eBXv。

Python 数值类型

Python 提供了基本的数值类型，如任意大小的整数和浮点数（双精度）作为标准，但它还提供了几种在精度特别重要的特定应用中有用的附加类型。Python 还提供了对复数的（内置）支持，这对一些更高级的数学应用很有用。

十进制类型

对于需要精确算术运算的十进制数字的应用，可以使用 Python 标准库中的decimal模块中的Decimal类型：

from decimal import Decimal
num1 = Decimal('1.1')
num2 = Decimal('1.563')
num1 + num2  # Decimal('2.663')

使用浮点对象进行此计算会得到结果 2.6630000000000003，这包括了一个小误差，这是因为某些数字不能用有限的 2 的幂的和来精确表示。例如，0.1 的二进制展开是 0.000110011…，它不会终止。因此，这个数字的任何浮点表示都会带有一个小误差。请注意，Decimal的参数是一个字符串，而不是一个浮点数。

Decimal 类型基于 IBM 通用十进制算术规范（speleotrove.com/decimal/decarith.html），这是一种浮点算术的替代规范，它通过使用 10 的幂而不是 2 的幂来精确表示十进制数。这意味着它可以安全地用于金融计算，其中舍入误差的累积将产生严重后果。然而，Decimal 格式的内存效率较低，因为它必须存储十进制数字而不是二进制数字（位），并且比传统的浮点数更加计算密集。

decimal 包还提供了一个Context对象，它允许对Decimal对象的精度、显示和属性进行精细控制。可以使用decimal模块的getcontext函数访问当前（默认）上下文。getcontext返回的Context对象具有许多可以修改的属性。例如，我们可以设置算术运算的精度：

from decimal import getcontext
ctx = getcontext()
num = Decimal('1.1')
num**4  # Decimal('1.4641')
ctx.prec = 4 # set new precision
num**4  # Decimal('1.464')

当我们将精度设置为 4 时，而不是默认的 28，我们会发现 1.1 的四次方被舍入为 4 个有效数字。

甚至可以使用localcontext函数在本地设置上下文，该函数返回一个上下文管理器，在with块结束时恢复原始环境：

from decimal import localcontext
num = Decimal("1.1")
with localcontext() as ctx:
    ctx.prec = 2
    num**4  # Decimal('1.5')
num**4  # Decimal('1.4641')

这意味着上下文可以在with块内自由修改，并且在结束时将返回默认值。

分数类型

或者，对于需要准确表示整数分数的应用程序，例如处理比例或概率时，可以使用 Python 标准库中 fractions 模块的 Fraction 类型。用法类似，只是我们通常将分数的分子和分母作为参数给出：

from fractions import Fraction
num1 = Fraction(1, 3)
num2 = Fraction(1, 7)
num1 * num2  # Fraction(1, 21)

Fraction 类型只是简单地存储两个整数，即分子和分母，并且使用分数的加法和乘法的基本规则执行算术运算。

复数类型

Python 也支持复数，包括在代码中表示复数单位 1j 的文字字符。这可能与您从其他复数源上熟悉的表示复数单位的习语不同。大多数数学文本通常会使用符号 i 来表示复数单位：

z = 1 + 1j
z + 2  # 3 + 1j
z.conjugate()  # 1 - 1j

Python 标准库的 cmath 模块提供了专门针对“复数” - 意识的数学函数。

基本数学函数

基本数学函数出现在许多应用程序中。例如，对数可以用于将呈指数增长的数据缩放为线性数据。指数函数和三角函数在处理几何信息时是常见的固定内容，gamma 函数 出现在组合学中，高斯误差函数 在统计学中很重要*.*

Python 标准库中的 math 模块提供了所有标准数学函数，以及常见常数和一些实用函数，可以使用以下命令导入：

import math

一旦导入，我们可以使用此模块中包含的任何数学函数。例如，要找到非负数的平方根，我们将使用 math 中的 sqrt 函数：

import math
math.sqrt(4)  #  2.0

尝试使用 sqrt 函数的负参数将引发 ValueError。这个 sqrt 函数不定义负数的平方根，它只处理实数。负数的平方根——这将是一个复数——可以使用 Python 标准库中 cmath 模块的替代 sqrt 函数找到。

三角函数，正弦、余弦和正切，在math模块中分别以它们的常见缩写sin、cos和tan可用。pi 常数保存了π的值，约为 3.1416：

theta = pi/4
math.cos(theta)  # 0.7071067811865476
math.sin(theta)  # 0.7071067811865475
math.tan(theta)  # 0.9999999999999999

math模块中的反三角函数分别命名为acos、asin和atan：

math.asin(-1)  # -1.5707963267948966
math.acos(-1)  # 3.141592653589793
math.atan(1)  # 0.7853981633974483

math模块中的log函数执行对数。它有一个可选参数来指定对数的底数（注意第二个参数只能是位置参数）。默认情况下，没有可选参数，它是以自然对数为底数e。e常数可以使用math.e来访问：

math.log(10) # 2.302585092994046
math.log(10, 10) # 1.0

math模块还包含gamma函数，即伽玛函数，以及erf函数，即高斯误差函数，这在统计学中非常重要。这两个函数都是通过积分来定义的。伽玛函数由积分定义

误差函数由下式定义

误差函数定义中的积分无法使用微积分来求解，而必须通过数值计算来完成：

math.gamma(5) # 24.0
math.erf(2) # 0.9953222650189527

除了标准函数，如三角函数、对数和指数函数之外，math模块还包含各种理论和组合函数。这些包括comb和factorial函数，它们在各种应用中非常有用。使用参数n和k调用的comb函数返回从n个项目的集合中选择k个项目的方式数，如果顺序不重要且没有重复。例如，先选择 1 再选择 2 与先选择 2 再选择 1 是相同的。这个数字有时被写为*^nC[k]。使用参数n调用的阶乘函数返回阶乘n! = n(n-1)(n-2)*…1：

math.comb(5, 2)  # 10
math.factorial(5)  # 120

对负数应用阶乘会引发ValueError。整数n的阶乘与n + 1处的伽玛函数的值相符，即

math模块还包含一个返回其参数的最大公约数的函数，称为gcd。a和b的最大公约数是最大的整数k，使得k能够完全整除a和b：

math.gcd(2, 4)  # 2
math.gcd(2, 3)  # 1

还有一些用于处理浮点数的函数。fsum函数对数字的可迭代对象执行加法，并在每一步跟踪总和，以减少结果中的误差。以下示例很好地说明了这一点：

nums = [0.1]*10  # list containing 0.1 ten times
sum(nums)  # 0.9999999999999999
math.fsum(nums)  # 1.0

isclose函数返回True，如果参数之间的差小于公差。这在单元测试中特别有用，因为基于机器架构或数据变异性，结果可能会有小的变化。

最后，math中的floor和ceil函数提供了它们的参数的下限和上限。数字x的floor是最大的整数f，使得f ≤ x，x的ceiling是最小的整数c，使得x ≤ c。在将一个数字除以另一个数字得到浮点数和整数之间转换时，这些函数非常有用。

math模块包含了在 C 中实现的函数（假设你正在运行 CPython），因此比在 Python 中实现的函数要快得多。如果你需要将函数应用于一个相对较小的数字集合，这个模块是一个不错的选择。如果你想要同时将这些函数应用于大量数据集合，最好使用 NumPy 包中的等效函数，这些函数对数组的处理更有效率。总的来说，如果你已经导入了 NumPy 包，那么最好总是使用这些函数的 NumPy 等效函数，以减少出错的机会。

NumPy 数组

NumPy 提供了高性能的数组类型和用于在 Python 中操作这些数组的例程。这些数组对于处理性能至关重要的大型数据集非常有用。NumPy 构成了 Python 中的数值和科学计算堆栈的基础。在幕后，NumPy 利用低级库来处理向量和矩阵，例如基本线性代数子程序（BLAS）包，以及线性代数包（LAPACK）包含更高级的线性代数例程。

传统上，NumPy 包是使用更短的别名np导入的，可以使用以下import语句来实现：

import numpy as np

特别是在 NumPy 文档和更广泛的科学 Python 生态系统（SciPy、Pandas 等）中使用了这种约定。

NumPy 库提供的基本类型是ndarray类型（以下简称 NumPy 数组）。通常，您不会创建此类型的自己的实例，而是使用array之类的辅助例程之一来正确设置类型。array例程从类似数组的对象创建 NumPy 数组，这通常是一组数字或一组（数字）列表。例如，我们可以通过提供包含所需元素的列表来创建一个简单的数组：

ary = np.array([1, 2, 3, 4])  # array([1, 2, 3, 4])

NumPy 数组类型（ndarray）是围绕基础 C 数组结构的 Python 包装器。数组操作是用 C 实现的，并针对性能进行了优化。NumPy 数组必须由同质数据组成（所有元素具有相同的类型），尽管此类型可以是指向任意 Python 对象的指针。如果在创建时未明确提供使用dtype关键字参数，则 NumPy 将推断出适当的数据类型：

np.array([1, 2, 3, 4], dtype=np.float32)
# array([1., 2., 3., 4.], dtype=float32)

在幕后，任何形状的 NumPy 数组都是一个包含原始数据的缓冲区，作为一个平坦（一维）数组，并包含一系列额外的元数据，用于指定诸如元素类型之类的细节。

创建后，可以使用数组的dtype属性访问数据类型。修改dtype属性将产生不良后果，因为构成数组中的原始字节将被重新解释为新的数据类型。例如，如果我们使用 Python 整数创建数组，NumPy 将在数组中将其转换为 64 位整数。更改dtype值将导致 NumPy 将这些 64 位整数重新解释为新的数据类型：

arr = np.array([1, 2, 3, 4])
print(arr.dtype) # dtype('int64')
arr.dtype = np.float32
print(arr)
# [1.e-45 0.e+00 3.e-45 0.e+00 4.e-45 0.e+00 6.e-45 0.e+00]

每个 64 位整数都被重新解释为两个 32 位浮点数，这显然会产生无意义的值。相反，如果您希望在创建后更改数据类型，请使用astype方法指定新类型。更改数据类型的正确方法如下所示：

arr = arr.astype(np.float32)
print(arr)
# [1\. 2\. 3\. 4.]

NumPy 还提供了一些用于创建各种标准数组的例程。zeros例程创建一个指定形状的数组，其中每个元素都是0，而ones例程创建一个数组，其中每个元素都是1。

元素访问

NumPy 数组支持getitem协议，因此可以像列表一样访问数组中的元素，并支持所有按组件执行的算术操作。这意味着我们可以使用索引表示法和索引来检索指定索引处的元素，如下所示：

ary = np.array([1, 2, 3, 4])
ary[0]  # 1
ary[2]  # 3

这还包括从现有数组中提取数据数组的常规切片语法。数组的切片再次是一个数组，其中包含切片指定的元素。例如，我们可以检索包含ary的前两个元素的数组，或者包含偶数索引处的元素的数组，如下所示：

first_two = ary[:2]  # array([1, 2])
even_idx = ary[::2]  # array([1, 3])

切片的语法是start:stop:step。我们可以省略start和stop中的一个或两个，以从所有元素的开头或结尾分别获取。我们也可以省略step参数，这种情况下我们也会去掉尾部的:。step参数描述了应该选择的选定范围内的元素。值为1选择每个元素，或者如本例中，值为2选择每第二个元素（从0开始给出偶数编号的元素）。这个语法与切片 Python 列表的语法相同。

数组的算术和函数

NumPy 提供了许多通用函数（ufunc），这些函数可以高效地操作 NumPy 数组类型。特别是，在基本数学函数部分讨论的所有基本数学函数在 NumPy 中都有类似的函数，可以在 NumPy 数组上操作。通用函数还可以执行广播，以允许它们在不同但兼容的形状的数组上进行操作。

NumPy 数组上的算术运算是逐分量执行的。以下示例最能说明这一点：

arr_a = np.array([1, 2, 3, 4])
arr_b = np.array([1, 0, -3, 1])
arr_a + arr_b  # array([2, 2, 0, 5])
arr_a - arr_b  # array([0, 2, 6, 3])
arr_a * arr_b  # array([ 1, 0, -9, 4])
arr_b / arr_a  # array([ 1\. , 0\. , -1\. , 0.25])
arr_b**arr_a  # array([1, 0, -27, 1])

请注意，数组必须具有相同的形状，这意味着具有相同的长度。对不同形状的数组进行算术运算将导致ValueError。通过数字进行加法、减法、乘法或除法将导致数组，其中已对每个分量应用了操作。例如，我们可以使用以下命令将数组中的所有元素乘以2：

arr = np.array([1, 2, 3, 4])
new = 2*arr
print(new)
# [2, 4, 6, 8]

有用的数组创建例程

要在两个给定端点之间以规则间隔生成数字数组，可以使用arange例程或linspace例程。这两个例程之间的区别在于linspace生成一定数量（默认为 50）的值，这些值在两个端点之间具有相等的间距，包括两个端点，而arange生成给定步长的数字，但不包括上限。linspace例程生成封闭区间a ≤ x ≤ b中的值，而arange例程生成半开区间a≤ x < b中的值：

np.linspace(0, 1, 5)  # array([0., 0.25, 0.5, 0.75, 1.0])
np.arange(0, 1, 0.3)  # array([0.0, 0.3, 0.6, 0.9])

请注意，使用linspace生成的数组恰好有 5 个点，由第三个参数指定，包括0和1两个端点。使用arange生成的数组有 4 个点，不包括右端点1；0.3 的额外步长将等于 1.2，这比 1 大。

更高维度的数组

NumPy 可以创建任意维度的数组，使用与简单一维数组相同的array例程创建。数组的维数由提供给array例程的嵌套列表的数量指定。例如，我们可以通过提供一个列表的列表来创建一个二维数组，其中内部列表的每个成员都是一个数字，如下所示：

mat = np.array([[1, 2], [3, 4]])

NumPy 数组具有shape属性，描述了每个维度中元素的排列方式。对于二维数组，形状可以解释为数组的行数和列数。

*NumPy 将形状存储为数组对象上的shape属性，这是一个元组。这个元组中的元素数量就是数组的维数：

vec = np.array([1, 2])
mat.shape  # (2, 2)
vec.shape  # (2,)

由于 NumPy 数组中的数据存储在一个扁平（一维）数组中，可以通过简单地更改相关的元数据来以很小的成本重新塑造数组。这是通过 NumPy 数组的reshape方法完成的：

mat.reshape(4,)  # array([1, 2, 3, 4])

请注意，元素的总数必须保持不变。矩阵mat最初的形状为(2, 2)，共有 4 个元素，后者是一个形状为(4,)的一维数组，再次共有 4 个元素。当总元素数量不匹配时，尝试重新塑造将导致ValueError。

要创建更高维度的数组，只需添加更多级别的嵌套列表。为了更清楚地说明这一点，在下面的示例中，我们在构造数组之前将第三维度中的每个元素的列表分开：

mat1 = [[1, 2], [3, 4]]
mat2 = [[5, 6], [7, 8]]
mat3 = [[9, 10], [11, 12]]
arr_3d = np.array([mat1, mat2, mat3])
arr_3d.shape  # (3, 2, 2)

请注意，形状的第一个元素是最外层的，最后一个元素是最内层的。

这意味着向数组添加一个额外的维度只是提供相关的元数据。使用array例程，shape元数据由参数中每个列表的长度描述。最外层列表的长度定义了该维度的相应shape参数，依此类推。

NumPy 数组在内存中的大小并不显著取决于维度的数量，而只取决于元素的总数，这是shape参数的乘积。但是，请注意，高维数组中的元素总数往往较大。

要访问多维数组中的元素，您可以使用通常的索引表示法，但是不是提供单个数字，而是需要在每个维度中提供索引。对于 2×2 矩阵，这意味着指定所需元素的行和列：

mat[0, 0]  # 1 - top left element
mat[1, 1]  # 4 - bottom right element

索引表示法还支持在每个维度上进行切片，因此我们可以使用切片mat[:, 0]提取单列的所有成员，如下所示：

mat[:, 0]
# array([1, 3])

请注意，切片的结果是一个一维数组。

数组创建函数zeros和ones可以通过简单地指定一个具有多个维度参数的形状来创建多维数组。

矩阵

NumPy 数组也可以作为矩阵，在数学和计算编程中是基本的。矩阵只是一个二维数组。矩阵在许多应用中都是核心，例如几何变换和同时方程，但也出现在其他领域的有用工具中，例如统计学。矩阵本身只有在我们为它们配备矩阵算术时才是独特的（与任何其他数组相比）。矩阵具有逐元素的加法和减法运算，就像 NumPy 数组一样，还有一种称为标量乘法的第三种运算，其中我们将矩阵的每个元素乘以一个常数，以及一种不同的矩阵乘法概念。矩阵乘法与其他乘法概念根本不同，我们稍后会看到。

矩阵的一个最重要的属性是其形状，与 NumPy 数组的定义完全相同。具有m行和n列的矩阵通常被描述为m×n矩阵。具有与列数相同的行数的矩阵被称为方阵，这些矩阵在向量和矩阵理论中起着特殊的作用。

单位矩阵（大小为n）是n×n矩阵，其中（i，i）-th 条目为 1，而（i，j）-th 条目对于i ≠ j为零。有一个数组创建例程，为指定的n值提供n×n单位矩阵：

np.eye(3)
# array([[1., 0., 0.],
#        [0., 1., 0.],
#        [0., 0., 1.]])

基本方法和属性

与矩阵相关的术语和数量有很多。我们在这里只提到两个这样的属性，因为它们以后会有用。这些是矩阵的转置，其中行和列互换，以及迹，它是方阵沿着主对角线的元素之和。主对角线由从矩阵左上角到右下角的线上的元素*a[ii]*组成。

NumPy 数组可以通过在array对象上调用transpose方法轻松转置。实际上，由于这是一个常见的操作，数组有一个方便的属性T，它返回矩阵的转置。转置会颠倒矩阵（数组）的形状顺序，使行变为列，列变为行。例如，如果我们从一个 3×2 矩阵（3 行，2 列）开始，那么它的转置将是一个 2×3 矩阵，就像下面的例子一样：

mat = np.array([[1, 2], [3, 4]])
mat.transpose()
# array([[1, 3],
#       [2, 4]])
mat.T
# array([[1, 3],
#       [2, 4]])

与矩阵相关的另一个数量有时也是有用的是trace。方阵A的 trace，其条目如前面的代码所示，被定义为leading diagonal上的元素之和，它由从左上角对角线到右下角的元素组成。trace 的公式如下*

*

NumPy 数组有一个trace方法，返回矩阵的迹：

A = np.array([[1, 2], [3, 4]])
A.trace()  # 5

trace 也可以使用np.trace函数访问，它不绑定到数组。

矩阵乘法

矩阵乘法是在两个矩阵上执行的操作，它保留了两个矩阵的一些结构和特性。形式上，如果A是一个l × m矩阵，B是一个m × n矩阵，如下所述

那么矩阵积A和B是一个l × n矩阵，其(p, q)-th 条目由下式给出

请注意，第一个矩阵的列数必须与第二个矩阵的行数匹配，以便定义矩阵乘法。如果定义了矩阵乘积AB，我们通常写AB，如果它被定义。矩阵乘法是一种特殊的操作。它不像大多数其他算术运算那样是交换的：即使AB和BA都可以计算，它们不一定相等。实际上，这意味着矩阵的乘法顺序很重要。这源自矩阵代数作为线性映射的表示的起源，其中乘法对应于函数的组合。

Python 有一个保留给矩阵乘法的运算符@，这是在 Python 3.5 中添加的。NumPy 数组实现了这个运算符来执行矩阵乘法。请注意，这与数组的分量乘法*在本质上是不同的：

A = np.array([[1, 2], [3, 4]])
B = np.array([[-1, 1], [0, 1]])
A @ B
# array([[-1, 3], 
#        [-3, 7]])
A * B # different from A @ B
# array([[-1, 2], 
#        [ 0, 4]])

单位矩阵是矩阵乘法下的中性元素。也就是说，如果A是任意的l × m矩阵，I是m × m单位矩阵，则AI = A。可以使用 NumPy 数组轻松检查特定示例：

A = np.array([[1, 2], [3, 4]])
I = np.eye(2)
A @ I
# array([[1, 2],
#        [3, 4]])

行列式和逆

一个方阵的determinant在大多数应用中都很重要，因为它与找到矩阵的逆的强连接。如果行和列的数量相等，则矩阵是方阵。特别地，一个具有非零行列式的矩阵具有（唯一的）逆，这对于某些方程组的唯一解是成立的。矩阵的行列式是递归定义的。对于一个 2×2 矩阵

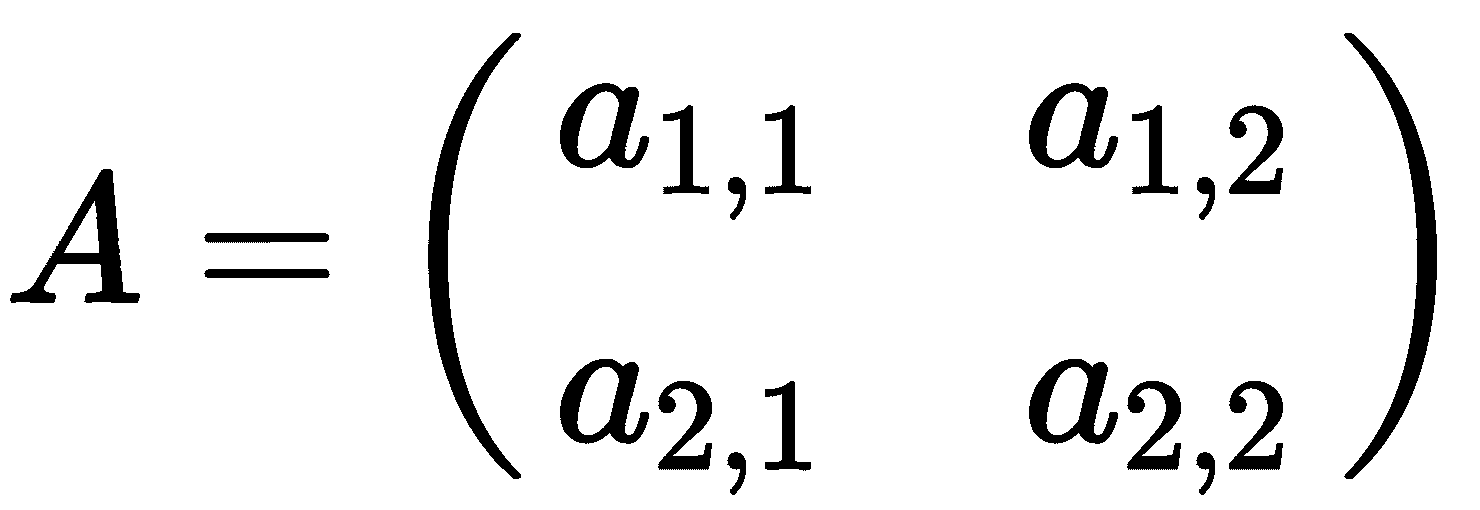
矩阵A的determinant由以下公式定义

对于一个一般的n×n矩阵

其中n > 2，我们定义子矩阵A[i,j]，对于 1 ≤ i，j ≤ n，为从A中删除第i行和第j列的结果。子矩阵A[i,j]是一个(n-1) × (n-1)矩阵，因此我们可以计算行列式。然后我们定义A的行列式为数量

实际上，出现在前述方程中的索引 1 可以被任何 1 ≤ i≤ n替换，结果将是相同的。

计算矩阵行列式的 NumPy 例程包含在一个名为linalg的单独模块中。这个模块包含了许多关于线性代数的常见例程，线性代数是涵盖向量和矩阵代数的数学分支。计算方阵行列式的例程是det例程：

from numpy import linalg
linalg.det(A)  # -2.0000000000000004

请注意，在计算行列式时发生了浮点舍入误差。

如果安装了 SciPy 包，还提供了一个扩展了 NumPylinalg的linalg模块。SciPy 版本不仅包括额外的例程，而且始终使用 BLAS 和 LAPACK 支持进行编译，而对于 NumPy 版本，这是可选的。因此，如果速度很重要，SciPy 变体可能更可取，这取决于 NumPy 的编译方式。

n × n矩阵A的逆是（必然唯一的）n × n矩阵B，使得AB=BA=I，其中I表示n × n单位矩阵，这里执行的乘法是矩阵乘法。并非每个方阵都有逆；那些没有逆的有时被称为奇异矩阵。事实上，当A没有逆时，也就是说，当该矩阵的行列式为 0 时，它是非奇异的。当A有逆时，习惯上用*A^(-1)*表示它。

linalg模块的inv例程计算矩阵的逆，如果存在的话：

linalg.inv(A)
# array([[-2\. , 1\. ],
#        [ 1.5, -0.5]])

我们可以通过矩阵乘法（在任一侧）乘以逆矩阵，并检查我们是否得到了 2 × 2 单位矩阵，来检查inv例程给出的矩阵是否确实是A的矩阵逆：

Ainv = linalg.inv(A)
Ainv @ A
# Approximately
# array([[1., 0.],
#        [0., 1.]])
A @ Ainv
# Approximately
# array([[1., 0.],
#        [0., 1.]])

这些计算中会有浮点误差，这已经被隐藏在Approximately注释后面，这是由于计算矩阵的逆的方式。

linalg包还包含许多其他方法，如norm，它计算矩阵的各种范数。它还包含了各种分解矩阵和解方程组的函数。

还有指数函数expm、对数函数logm、正弦函数sinm、余弦函数cosm和切线函数tanm的矩阵类比。请注意，这些函数与基本 NumPy 包中的标准exp、log、sin、cos和tan函数不同，后者是在元素基础上应用相应的函数。相反，矩阵指数函数是使用矩阵的“幂级数”定义的。

其中A是一个n × n矩阵，A^k是A的第k个矩阵幂；也就是说，A矩阵连续乘以自身k次。请注意，这个“幂级数”总是在适当的意义下收敛。按照惯例，我们取A⁰ = I，其中I是n × n单位矩阵。这与实数或复数的指数函数的常规幂级数定义完全类似，但是用矩阵和矩阵乘法代替了数字和（常规）乘法。其他函数也是以类似的方式定义的，但我们将跳过细节。

方程组

解（线性）方程组是研究矩阵的主要动机之一。这类问题在各种应用中经常出现。我们从写成线性方程组的形式开始

其中n至少为 2，*a[i,j]和b[i]*是已知值，*x[i]*值是我们希望找到的未知值。

在解这样的方程组之前，我们需要将问题转化为矩阵方程。这是通过将系数a[i,j]收集到一个n × n矩阵中，并使用矩阵乘法的性质将这个矩阵与方程组联系起来实现的。因此，让

是包含方程中系数的矩阵。然后，如果我们将x作为未知数（列）向量，包含x[i]值，b作为（列）向量，包含已知值b[i]，那么我们可以将方程组重写为单个矩阵方程

现在我们可以使用矩阵技术来解决这个问题。在这种情况下，我们将列向量视为n × 1矩阵，因此前面方程中的乘法是矩阵乘法。为了解决这个矩阵方程，我们使用linalg模块中的solve例程。为了说明这种技术，我们将解决以下方程组作为示例：

这些方程有三个未知值，x[1]，x[2]和x[3]。首先，我们创建系数矩阵和向量b。由于我们使用 NumPy 来处理矩阵和向量，我们为矩阵A创建一个二维 NumPy 数组，为b创建一个一维数组：

import numpy as np
from numpy import linalg

A = np.array([[3, -2, 1], [1, 1, -2], [-3, -2, 1]])
b = np.array([7, -4, 1])

现在，可以使用solve例程找到方程组的解：

linalg.solve(A, b)  # array([ 1., -1., 2.])

这确实是方程组的解，可以通过计算A @ x并将结果与b数组进行对比来轻松验证。在这个计算中可能会出现浮点舍入误差。

solve函数需要两个输入，即系数矩阵A和右侧向量b。它使用 LAPACK 例程解决方程组，将矩阵A分解为更简单的矩阵，以快速减少为一个可以通过简单替换解决的更简单的问题。这种解决矩阵方程的技术非常强大和高效，并且不太容易受到浮点舍入误差的影响。例如，可以通过与矩阵A的逆矩阵相乘（在左侧）来计算方程组的解，如果已知逆矩阵。然而，这通常不如使用solve例程好，因为它可能更慢或导致更大的数值误差。

在我们使用的示例中，系数矩阵A是方阵。也就是说，方程的数量与未知值的数量相同。在这种情况下，如果且仅当矩阵A的行列式不为 0 时，方程组有唯一解。在矩阵A的行列式为 0 的情况下，可能会出现两种情况：方程组可能没有解，这种情况下我们称方程组是不一致的；或者可能有无穷多个解。一致和不一致系统之间的区别通常由向量b决定。例如，考虑以下方程组：

左侧的方程组是一致的，有无穷多个解；例如，取x = 1 和y = 1或x = 0和y = 2都是解。右侧的方程组是不一致的，没有解。在上述两种情况下，solve例程将失败，因为系数矩阵是奇异的。

系数矩阵不需要是方阵才能解决方程组。例如，如果方程比未知值多（系数矩阵的行数多于列数）。这样的系统被称为过度规定，只要是一致的，它就会有解。如果方程比未知值少，那么系统被称为不足规定。如果是一致的，不足规定的方程组通常有无穷多个解，因为没有足够的信息来唯一指定所有未知值。不幸的是，即使系统有解，solve例程也无法找到系数矩阵不是方阵的系统的解。

特征值和特征向量

考虑矩阵方程Ax = λx，其中A是一个方阵（n × n），x是一个向量，λ是一个数字。对于这个方程有一个x可以解决的λ被称为特征值，相应的向量x被称为特征向量。特征值和相应的特征向量对编码了关于矩阵A的信息，因此在许多矩阵出现的应用中非常重要。

我们将演示使用以下矩阵计算特征值和特征向量：

我们必须首先将其定义为 NumPy 数组：

import numpy as np
from numpy import linalg
A = np.array([[3, -1, 4], [-1, 0, -1], [4, -1, 2]])

linalg模块中的eig例程用于找到方阵的特征值和特征向量。这个例程返回一对(v, B)，其中v是包含特征值的一维数组，B是其列是相应特征向量的二维数组：

v, B = linalg.eig(A)

只有具有实数条目的矩阵才可能具有复特征值和特征向量。因此，eig例程的返回类型有时将是复数类型，如complex32或complex64。在某些应用中，复特征值具有特殊含义，而在其他情况下，我们只考虑实特征值。

我们可以使用以下序列从eig的输出中提取特征值/特征向量对：

i = 0 # first eigenvalue/eigenvector pair
lambda0 = v[i]
print(lambda0)
# 6.823156164525971
x0 = B[:, i] # ith column of B
print(x0)
# array([ 0.73271846, -0.20260301, 0.649672352])

eig例程返回的特征向量是归一化的，使得它们的范数（长度）为 1。 （欧几里得范数被定义为数组成员的平方和的平方根。）我们可以通过使用linalg中的norm例程计算向量的范数来检查这一点：

linalg.norm(x0)  # 1.0  - eigenvectors are normalized.

最后，我们可以通过计算乘积A @ x0并检查，直到浮点精度，这等于lambda0*x0，来检查这些值确实满足特征值/特征向量对的定义：

lhs = A @ x0
rhs = lambda0*x0
linalg.norm(lhs - rhs)  # 2.8435583831733384e-15 - very small.

这里计算的范数表示方程Ax = λx的左侧lhs和右侧rhs之间的“距离”。由于这个距离非常小（小数点后 0 到 14 位），我们可以相当确信它们实际上是相同的。这不为零的事实可能是由于浮点精度误差。

eig例程是围绕低级 LAPACK 例程的包装器，用于计算特征值和特征向量。找到特征值和特征向量的理论过程是首先通过解方程找到特征值

其中I是适当的单位矩阵，以找到值λ。左侧确定的方程是λ的多项式，称为A的特征多项式。然后可以通过解决矩阵方程找到相应的特征向量

其中λ*[j]*是已经找到的特征值之一。实际上，这个过程有些低效，有替代策略可以更有效地计算特征值和特征向量。

特征值和特征向量的一个关键应用是主成分分析，这是一种将大型复杂数据集减少到更好地理解内部结构的关键技术。

我们只能计算方阵的特征值和特征向量；对于非方阵，该定义没有意义。有一种将特征值和特征值推广到非方阵的称为奇异值的方法。

稀疏矩阵

诸如前面讨论的那样的线性方程组在数学中非常常见，特别是在数学计算中。在许多应用中，系数矩阵将非常庞大，有数千行和列，并且可能来自替代来源而不是简单地手动输入。在许多情况下，它还将是稀疏矩阵，其中大多数条目为 0。

如果矩阵的大多数元素为零，则矩阵是稀疏的。要调用矩阵稀疏，需要为零的确切元素数量并不明确定义。稀疏矩阵可以更有效地表示，例如，只需存储非零的索引（i，j）和值a[i,j]。有整个集合的稀疏矩阵算法，可以在矩阵确实足够稀疏的情况下大大提高性能。

稀疏矩阵出现在许多应用程序中，并且通常遵循某种模式。特别是，解决偏微分方程（PDEs）的几种技术涉及解决稀疏矩阵方程（请参阅第三章，微积分和微分方程），与网络相关的矩阵通常是稀疏的。sparse.csgraph模块中包含与网络（图）相关的稀疏矩阵的其他例程。我们将在第五章中进一步讨论这些内容，处理树和网络。

sparse模块包含几种表示稀疏矩阵存储方式的不同类。存储稀疏矩阵的最基本方式是存储三个数组，其中两个包含表示非零元素的索引的整数，第三个包含相应元素的数据。这是coo_matrix类的格式。然后有压缩列 CSC（csc_matrix）和压缩行 CSR（csr_matrix）格式，它们分别提供了有效的列或行切片。sparse中还有三个额外的稀疏矩阵类，包括dia_matrix，它有效地存储非零条目沿对角线带出现的矩阵。

来自 SciPy 的sparse模块包含用于创建和处理稀疏矩阵的例程。我们使用以下import语句从 SciPy 导入sparse模块：

import numpy as np
from scipy import sparse

稀疏矩阵可以从完整（密集）矩阵或其他某种数据结构创建。这是使用特定格式的构造函数来完成的，您希望将稀疏矩阵存储在其中。

例如，我们可以通过使用以下命令将密集矩阵存储为 CSR 格式：

A = np.array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
sp_A = sparse.csr_matrix(A)

如果您手动生成稀疏矩阵，该矩阵可能遵循某种模式，例如以下三对角矩阵：

在这里，非零条目出现在对角线上以及对角线两侧，并且每行中的非零条目遵循相同的模式。要创建这样的矩阵，我们可以使用sparse中的数组创建例程之一，例如diags，这是一个用于创建具有对角线模式的矩阵的便利例程：

T = sparse.diags([-1, 2, -1], (-1, 0, 1), shape=(5, 5), format="csr")

这将创建矩阵T，并按压缩稀疏行 CSR 格式存储它。第一个参数指定应出现在输出矩阵中的值，第二个参数是相对于应放置值的对角线位置的位置。因此，元组中的 0 索引表示对角线条目，-1 表示在行中对角线的左侧，+1 表示在行中对角线的右侧。shape关键字参数给出了生成的矩阵的维度，format指定了矩阵的存储格式。如果没有使用可选参数提供格式，则将使用合理的默认值。数组T可以使用toarray方法扩展为完整（密集）矩阵：

T.toarray()
# array([[ 2, -1,  0,  0,  0],
#        [-1,  2, -1,  0,  0],
#        [ 0, -1,  2, -1,  0],
#        [ 0,  0, -1,  2, -1],
#        [ 0,  0,  0, -1,  2]])

当矩阵很小时（就像这里一样），稀疏求解例程和通常的求解例程之间的性能差异很小。

一旦矩阵以稀疏格式存储，我们可以使用sparse的linalg子模块中的稀疏求解例程。例如，我们可以使用该模块的spsolve例程来解决矩阵方程。spsolve例程将把矩阵转换为 CSR 或 CSC，如果矩阵不是以这些格式之一提供的话，可能会增加额外的计算时间：

from scipy.sparse import linalg
linalg.spsolve(T.tocsr(), np.array([1, 2, 3, 4, 5]))
# array([ 5.83333333, 10.66666667, 13.5 , 13.33333333, 9.16666667])

sparse.linalg模块还包含许多可以在 NumPy（或 SciPy）的linalg模块中找到的接受稀疏矩阵而不是完整 NumPy 数组的例程，例如eig和inv。

摘要

Python 提供了对数学的内置支持，包括一些基本的数值类型、算术和基本的数学函数。然而，对于涉及大量数值值数组的更严肃的计算，您应该使用 NumPy 和 SciPy 软件包。NumPy 提供高性能的数组类型和基本例程，而 SciPy 提供了更多用于解方程和处理稀疏矩阵（以及许多其他内容）的特定工具。

NumPy 数组可以是多维的。特别是，二维数组具有矩阵属性，可以使用 NumPy 或 SciPy 的linalg模块（前者是后者的子集）来访问。此外，Python 中有一个特殊的矩阵乘法运算符@，它是为 NumPy 数组实现的。

在下一章中，我们将开始查看一些配方。

进一步阅读

有许多数学教科书描述矩阵和线性代数的基本属性，线性代数是研究向量和矩阵的学科。一个很好的入门文本是Blyth, T. and Robertson, E. (2013). Basic Linear Algebra**. London: Springer London, Limited。

NumPy 和 SciPy 是 Python 数学和科学计算生态系统的一部分，并且有广泛的文档可以从官方网站scipy.org访问。我们将在本书中看到这个生态系统中的几个其他软件包。

有关 NumPy 和 SciPy 在幕后使用的 BLAS 和 LAPACK 库的更多信息可以在以下链接找到：BLAS：www.netlib.org/blas/ 和 LAPACK：www.netlib.org/lapack/。

第三章：使用 Matplotlib 进行数学绘图

绘图是数学中的基本工具。一个好的图可以揭示隐藏的细节，建议未来的方向，验证结果或加强论点。因此，科学 Python 堆栈中拥有一个名为 Matplotlib 的强大而灵活的绘图库并不奇怪。

在本章中，我们将以各种样式绘制函数和数据，并创建完全标记和注释的图。我们将创建三维图，自定义图的外观，使用子图创建包含多个图的图，并直接将图保存到文件中，以供在非交互式环境中运行的应用程序使用。

在本章中，我们将涵盖以下示例：

• 使用 Matplotlib 进行基本绘图

• 更改绘图样式

• 为绘图添加标签和图例

• 添加子图

• 保存 Matplotlib 图

• 表面和等高线图

• 自定义三维图

技术要求

Python 的主要绘图包是 Matplotlib，可以使用您喜欢的软件包管理器（如pip）进行安装：

          python3.8 -m pip install matplotlib

这将安装最新版本的 Matplotlib，在撰写本书时，最新版本是 3.2.1。

Matplotlib 包含许多子包，但主要用户界面是matplotlib.pyplot包，按照惯例，它被导入为plt别名。可以使用以下导入语句来实现这一点：

import matplotlib.pyplot as plt

本章中的许多示例还需要 NumPy，通常情况下，它被导入为np别名。

本章的代码可以在 GitHub 存储库的Chapter 02文件夹中找到，网址为github.com/PacktPublishing/Applying-Math-with-Python/tree/master/Chapter%2002。

查看以下视频以查看代码实际操作：bit.ly/2ZOSuhs。

使用 Matplotlib 进行基本绘图

绘图是理解行为的重要部分。通过简单地绘制函数或数据，可以学到很多原本隐藏的东西。在这个示例中，我们将介绍如何使用 Matplotlib 绘制简单的函数或数据。

Matplotlib 是一个非常强大的绘图库，这意味着用它执行简单任务可能会令人畏惧。对于习惯于使用 MATLAB 和其他数学软件包的用户，有一个称为pyplot的基于状态的接口。还有一个面向对象的接口，对于更复杂的绘图可能更合适。pyplot接口是创建基本对象的便捷方式。

准备工作

通常情况下，要绘制的数据将存储在两个单独的 NumPy 数组中，我们将为了清晰起见将它们标记为x和y（尽管在实践中这个命名并不重要）。我们将演示绘制函数的图形，因此我们将生成一组x值的数组，并使用函数生成相应的y值。我们定义将要绘制的函数如下：

def f(x):
    return x*(x - 2)*np.exp(3 - x)

操作步骤

在我们绘制函数之前，我们必须生成要绘制的x和y数据。如果要绘制现有数据，可以跳过这些命令。我们需要创建一组覆盖所需范围的x值，然后使用函数创建y值：

1. NumPy 中的linspace例程非常适合创建用于绘图的数字数组。默认情况下，它将在指定参数之间创建 50 个等间距点。可以通过提供额外的参数来自定义点的数量，但对于大多数情况来说，50 就足够了。

x = np.linspace(-0.5, 3.0)  # 100 values between -0.5 and 3.0

1. 一旦我们创建了x值，就可以生成y值：

y = f(x)  # evaluate f on the x points

1. 要绘制数据，我们只需要从pyplot接口调用plot函数，该接口被导入为plt别名。第一个参数是x数据，第二个是y数据。该函数返回一个用于绘制数据的轴对象的句柄：

plt.plot(x, y)

1. 这将在新的图形上绘制y值与x值。如果你在 IPython 中工作或者使用 Jupyter 笔记本，那么图形应该会自动出现；否则，你可能需要调用plt.show函数来使图形出现：

plt.show()

如果使用plt.show，图形应该会出现在一个新窗口中。生成的图形应该看起来像图 2.1中的图形。你的默认绘图颜色可能与你的绘图不同。这是为了增加可见性而更改的默认绘图颜色：

图 2.1：使用 Matplotlib 绘制的函数的图形，没有任何额外的样式参数

我们不会在本章的其他配方中添加这个命令，但是你应该知道，如果你不是在自动渲染图形的环境中工作，比如在 IPython 控制台或 Jupyter Notebook 中，你将需要使用它。

工作原理…

如果当前没有Figure或Axes对象，plt.plot例程会创建一个新的Figure对象，向图形添加一个新的Axes对象，并用绘制的数据填充这个Axes对象。返回一个指向绘制线的句柄列表。每个句柄都是一个Lines2D对象。在这种情况下，这个列表将包含一个单独的Lines2D对象。我们可以使用这个Lines2D对象稍后自定义线的外观（参见更改绘图样式配方）。

Matplotlib 的对象层与较低级别的后端进行交互，后端负责生成图形绘图的繁重工作。plt.show函数发出指令给后端来渲染当前的图形。Matplotlib 可以使用多个后端，可以通过设置MPLBACKEND环境变量、修改matplotlibrc文件，或者在 Python 中调用matplotlib.use并指定替代后端的名称来自定义。

plt.show函数不仅仅是在图形上调用show方法。它还连接到一个事件循环，以正确显示图形。应该使用plt.show例程来显示图形，而不是在Figure对象上调用show方法。

还有更多…

有时候在调用plot例程之前手动实例化一个Figure对象是有用的，例如，强制创建一个新的图形。这个配方中的代码也可以写成如下形式：

fig = plt.figure()  # manually create a figure
lines = plt.plot(x, y)  # plot data

plt.plot例程接受可变数量的位置输入。在前面的代码中，我们提供了两个位置参数，它们被解释为x值和y值（按顺序）。如果我们只提供了一个单一的数组，plot例程会根据数组中的位置绘制数值；也就是说，x值被视为0、1、2等等。我们还可以提供多对数组来在同一坐标轴上绘制多组数据：

x = np.linspace(-0.5, 3.0)
lines = plt.plot(x, f(x), x, x**2, x, 1 - x)

前面代码的输出如下：

图 2.2：在 Matplotlib 中使用一次调用 plot 例程产生单个图形上的多个图形

有时候需要创建一个新的图形，并在该图形中显式地创建一组新的坐标轴。实现这一目标的最佳方法是使用pyplot接口中的subplots例程（参见添加子图配方）。这个例程返回一对对象，第一个对象是Figure，第二个对象是Axes：

fig, ax = plt.subplots()
l1 = ax.plot(x, f(x))
l2 = ax.plot(x, x**2)
l3 = ax.plot(x, 1 - x)

这一系列命令产生了与前面显示的图 2.2中相同的图形。

Matplotlib 除了这里描述的plot例程之外，还有许多其他绘图例程。例如，有一些绘图方法使用不同的比例尺来绘制坐标轴，包括分别使用对数x轴或对数y轴（semilogx或semilogy）或同时使用（loglog）。这些在 Matplotlib 文档中有解释。

更改绘图样式

Matplotlib 绘图的基本样式适用于绘制有序的函数或数据，但对于不按任何顺序呈现的离散数据来说，这种样式就不太合适了。为了防止 Matplotlib 在每个数据点之间绘制线条，我们可以将绘图样式更改为“关闭”线条绘制。在这个示例中，我们将通过向plot方法添加格式字符串参数来为坐标轴上的每条线自定义绘图样式。

准备工作

您需要将数据存储在数组对中。为了演示目的，我们将定义以下数据：

y1 = np.array([1.0, 2.0, 3.0, 4.0, 5.0])
y2 = np.array([1.2, 1.6, 3.1, 4.2, 4.8])
y3 = np.array([3.2, 1.1, 2.0, 4.9, 2.5])

我们将根据数组中的位置（即x坐标将分别为0、1、2、3或4）绘制这些点。

如何做到…

控制绘图样式的最简单方法是使用格式字符串，它作为plot命令中x-y对或plot命令中的ydata 后的可选参数提供。在绘制多组数据时，可以为每组参数提供不同的格式字符串。以下步骤提供了创建新图并在该图上绘制数据的一般过程：

*1. 我们首先使用pyplot中的subplots例程显式创建Figure和Axes对象：

fig, ax = plt.subplots()

1. 现在我们已经创建了Figure和Axes对象，可以使用Axes对象上的plot方法绘制数据。这个方法接受与pyplot中的plot例程相同的参数：

lines = ax.plot(y1, 'o', y2, 'x', y3, '*')

这将使用圆圈标记绘制第一个数据集（y1），使用x标记绘制第二个数据集（y2），使用星号（*）标记绘制第三个数据集（y3）。这个命令的输出显示在图 2.3中。格式字符串可以指定多种不同的标记线和颜色样式。如果我们改为使用pyplot接口中的plot例程，其调用签名与plot方法相同，也是一样的。

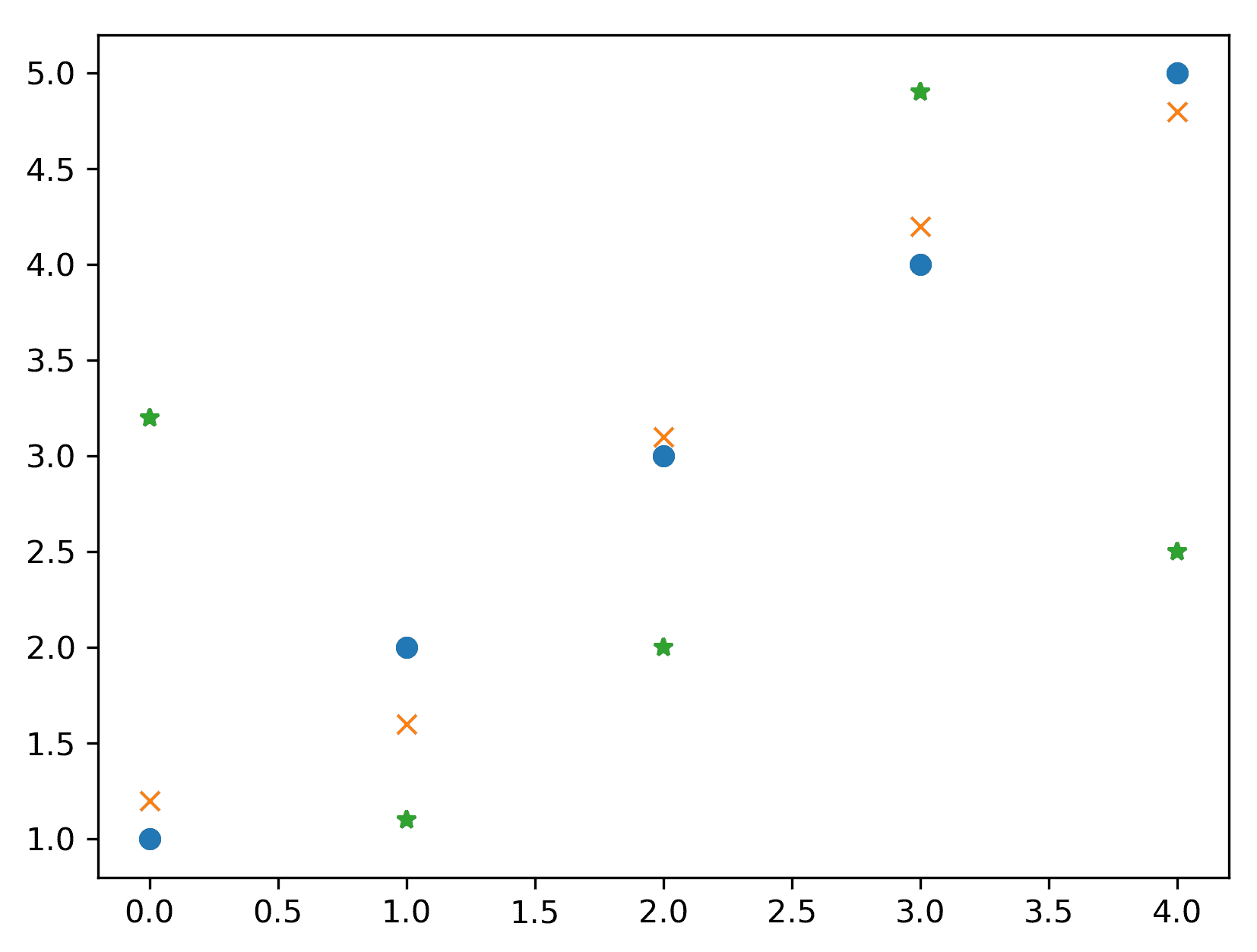
图 2.3：绘制三组数据，每组数据使用不同的标记样式绘制

它是如何工作的…

格式字符串有三个可选部分，每个部分由一个或多个字符组成。第一部分控制标记样式，即打印在每个数据点处的符号；第二部分控制连接数据点的线条样式；第三部分控制绘图的颜色。在这个示例中，我们只指定了标记样式，这意味着在相邻数据点之间不会绘制连接线。这对于绘制不需要在点之间进行插值的离散数据非常有用。有四种线条样式参数可用：实线（-）；虚线（--）；点划线（-.）；或点线（:）。格式字符串中只能指定有限数量的颜色；它们是红色、绿色、蓝色、青色、黄色、品红色、黑色和白色。格式字符串中使用的字符是每种颜色的第一个字母（黑色除外），因此相应的字符分别是r、g、b、c、y、m、k和w。

例如，如果我们只想更改标记样式，就像在这个示例中所做的那样，改为加号字符，我们将使用"+"格式字符串。如果我们还想将线条样式更改为点划线，我们将使用"+-."格式字符串。最后，如果我们还希望将标记的颜色更改为红色，我们将使用"+-.r"格式字符串。这些指定符也可以以其他配置提供，例如在标记样式之前指定颜色，但这可能会导致 Matplotlib 解析格式字符串的方式存在歧义。

如果您正在使用 Jupyter 笔记本和subplots命令，则必须在与绘图命令相同的单元格中包含对subplots的调用，否则图形将不会被生成。

还有更多…

plot方法还接受许多关键字参数，这些参数也可以用于控制图的样式。如果同时存在关键字参数和格式字符串参数，则关键字参数优先，并且它们适用于调用绘制的所有数据集。控制标记样式的关键字是marker，线型的关键字是linestyle，颜色的关键字是color。color关键字参数接受许多不同的格式来指定颜色，其中包括 RGB 值作为(r, g, b)元组，其中每个字符都是0到1之间的浮点数，或者是十六进制字符串。可以使用linewidth关键字控制绘制的线的宽度，应该提供一个float值。plot还可以传递许多其他关键字参数；在 Matplotlib 文档中列出了一个列表。这些关键字参数中的许多都有较短的版本，例如c代表color，lw代表linewidth。

例如，我们可以使用以下命令通过在调用plot时使用color关键字参数来设置配方中所有标记的颜色：

ax.plot(y1, 'o', y2, 'x', y3, '*', color="k")

从对plot方法（或plt.plot例程）的调用返回的Line2D对象也可以用于自定义每组数据的外观。例如，可以使用Line2D对象中的set_linestyle方法，使用适当的线型格式字符串设置线型。

可以使用Axes对象上的方法自定义图的其他方面。可以使用Axes对象上的set_xticks和set_yticks方法修改坐标轴刻度，可以使用grid方法配置网格外观。pyplot接口中还有方便的方法，可以将这些修改应用于当前坐标轴（如果存在）。

例如，我们修改轴限制，在x和y方向上的每个0.5的倍数设置刻度，并通过以下命令向图添加网格：

ax.axis([-0.5, 5.5, 0, 5.5]) # set axes
ax.set_xticks([0.5*i for i in range(9)])  # set xticks
ax.set_yticks([0.5*i for i in range(11)] # set yticks
ax.grid()  # add a grid

注意我们将限制设置为略大于图的范围。这是为了避免标记放在图窗口的边界上。

如果希望在轴上绘制离散数据而不连接点与线，则scatter绘图例程可能更好。这允许更多地控制标记的样式。例如，可以根据一些额外信息调整标记的大小。

向绘图添加标签和图例

每个图应该有一个标题，并且轴应该被正确标记。对于显示多组数据的图，图例是帮助读者快速识别不同数据集的标记、线条和颜色的好方法。在本示例中，我们将向图添加轴标签和标题，然后添加一个图例来帮助区分不同的数据集。为了保持代码简单，我们将绘制上一个示例中的数据。

如何做…

按照以下步骤向您的图添加标签和图例，以帮助区分它们代表的数据集：

1. 我们首先使用以下plot命令从上一个示例中重新创建图：

fig, ax = plt.subplots()
ax = ax.plot(y1, "o-", y2, "x--", y3, "*-.")

1. 现在，我们有了一个Axes对象的引用，我们可以开始通过添加标签和标题来自定义这些轴。可以使用subplots例程创建的ax对象上的set_title、set_xlabel和set_ylabel方法向图中添加标题和轴标签。在每种情况下，参数都是包含要显示的文本的字符串：

ax.set_title("Plot of the data y1, y2, and y3")
ax.set_xlabel("x axis label")
ax.set_ylabel("y axis label")

在这里，我们使用不同的样式绘制了三个数据集。标记样式与上一个示例中相同，但我们为第一个数据集添加了实线，为第二个数据集添加了虚线，为第三个数据集添加了点划线。

1. 要添加图例，我们在ax对象上调用legend方法。参数应该是一个包含每组数据在图例中的描述的元组或列表：

ax.legend(("data y1", "data y2", "data y3"))

上述一系列命令的结果如下：

图 2.4：使用 Matplotlib 生成的带有轴标签、标题和图例的图

工作原理…

set_title、set_xlabel和set_ylabel方法只是将文本参数添加到Axes对象的相应位置。如前面的代码中调用的legend方法，按照它们添加到图中的顺序添加标签，本例中为y1、y2，然后是y3。

可以提供一些关键字参数给set_title、set_xlabel和set_ylabel方法来控制文本的样式。例如，fontsize关键字可以用来指定标签字体的大小，通常使用pt点度量。还可以通过向例程提供usetex=True来使用 TeX 格式化标签。标签的 TeX 格式化在图 2.5中演示。如果标题或轴标签包含数学公式，这是非常有用的。不幸的是，如果系统上没有安装 TeX，就不能使用usetex关键字参数，否则会导致错误。但是，仍然可以使用 TeX 语法来格式化标签中的数学文本，但这将由 Matplotlib 而不是 TeX 来排版。

我们可以使用fontfamily关键字来使用不同的字体，其值可以是字体的名称或serif、sans-serif或monospace，它将选择适当的内置字体。可以在 Matplotlib 文档中找到matplotlib.text.Text类的完整修饰符列表。

要向图添加单独的文本注释，可以在Axes对象上使用annotate方法。这个例程接受两个参数——要显示的文本作为字符串和注释应放置的点的坐标。这个例程还接受前面提到的样式关键字参数。

添加子图

有时，将多个相关的图放在同一图中并排显示，但不在同一坐标轴上是很有用的。子图允许我们在单个图中生成一个网格的单独图。在这个示例中，我们将看到如何使用子图在单个图上并排创建两个图。

准备工作

您需要将要绘制在每个子图上的数据。例如，我们将在第一个子图上绘制应用于f(x) = x²-1函数的牛顿法的前五个迭代，初始值为x[0] = 2，对于第二个子图，我们将绘制迭代的误差。我们首先定义一个生成器函数来获取迭代：

def generate_newton_iters(x0, number):
    iterates = [x0]
    errors = [abs(x0 - 1.)]
    for _ in range(number):
        x0 = x0 - (x0*x0 - 1.)/(2*x0)
        iterates.append(x0)
        errors.append(abs(x0 - 1.))
    return iterates, errors

这个例程生成两个列表。第一个列表包含应用于函数的牛顿法的迭代，第二个包含近似值的误差：

iterates, errors = generate_newton_iters(2.0, 5)

如何做…

以下步骤显示了如何创建包含多个子图的图：

1. 我们使用subplots例程创建一个新的图和每个子图中的所有Axes对象的引用，这些子图在一个行和两个列的网格中排列。我们还将tight_layout关键字参数设置为True，以修复生成图的布局。这并不是严格必要的，但在这种情况下是必要的，因为它产生的结果比默认的更好：

fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True) # 1 row, 2 columns

1. 一旦创建了Figure和Axes对象，我们可以通过在每个Axes对象上调用相关的绘图方法来填充图。对于第一个图（显示在左侧），我们在ax1对象上使用plot方法，它与标准的plt.plot例程具有相同的签名。然后我们可以在ax1上调用set_title、set_xlabel和set_ylabel方法来设置标题和x和y标签。我们还通过提供usetex关键字参数来使用 TeX 格式化轴标签；如果您的系统上没有安装 TeX，可以忽略这一点：

ax1.plot(iterates, "x")
ax1.set_title("Iterates")
ax1.set_xlabel("$i$", usetex=True)
ax1.set_ylabel("$x_i$", usetex=True)

1. 现在，我们可以使用ax2对象在第二个图上（显示在右侧）绘制错误值。我们使用了一种使用对数刻度的替代绘图方法，称为semilogy。该方法的签名与标准的plot方法相同。同样，我们设置了轴标签和标题。如果没有安装 TeX，可以不使用usetex。

ax2.semilogy(errors, "x") # plot y on logarithmic scale
ax2.set_title("Error")
ax2.set_xlabel("$i$", usetex=True)
ax2.set_ylabel("Error")

这些命令序列的结果如下图所示：

图 2.5：Matplotlib 子图

左侧绘制了牛顿法的前五次迭代，右侧是以对数刻度绘制的近似误差。

工作原理…

Matplotlib 中的Figure对象只是一个特定大小的绘图元素（如Axes）的容器。Figure对象通常只包含一个Axes对象，该对象占据整个图形区域，但它可以在相同的区域中包含任意数量的Axes对象。subplots例程执行几项任务。首先创建一个新的图形，然后在图形区域内创建一个指定形状的网格。然后，在网格的每个位置添加一个新的Axes对象。然后将新的Figure对象和一个或多个Axes对象返回给用户。如果请求单个子图（一行一列，没有参数），则返回一个普通的Axes对象。如果请求单行或单列（分别具有多于一个列或行），则返回Axes对象的列表。如果请求多行和多列，则将返回一个列表的列表，其中行由填充有Axes对象的内部列表表示。然后我们可以使用每个Axes对象上的绘图方法来填充图形以显示所需的绘图。

在本示例中，我们在左侧使用了标准的plot方法，就像我们在以前的示例中看到的那样。但是，在右侧绘图中，我们使用了一个将y轴更改为对数刻度的绘图。这意味着y轴上的每个单位代表 10 的幂的变化，而不是一个单位的变化，因此0代表 10⁰=1，1代表 10，2代表 100，依此类推。轴标签会自动更改以反映这种比例变化。当值按数量级变化时，例如近似误差随着迭代次数的增加而变化时，这种缩放是有用的。我们还可以使用semilogx方法仅对x使用对数刻度进行绘制，或者使用loglog方法对两个轴都使用对数刻度进行绘制。

还有更多…

在 Matplotlib 中有几种创建子图的方法。如果已经创建了一个Figure对象，则可以使用Figure对象的add_subplot方法添加子图。或者，您可以使用matplotlib.pyplot中的subplot例程将子图添加到当前图。如果尚不存在，则在调用此例程时将创建一个新的图。subplot例程是Figure对象上add_subplot方法的便利包装。

要创建一个具有一个或多个子图的新图形，还可以使用pyplot接口中的subplots例程（如更改绘图样式中所示），它返回一个新的图形对象和一个Axes对象的数组，每个位置一个。这三种方法都需要子图矩阵的行数和列数。add_subplot方法和subplot例程还需要第三个参数，即要修改的子图的索引。返回当前子图的Axes对象。

在前面的例子中，我们创建了两个具有不同比例的y轴的图。这展示了子图的许多可能用途之一。另一个常见用途是在矩阵中绘制数据，其中列具有共同的x标签，行具有共同的y标签，这在多元统计中特别常见，用于研究各组数据之间的相关性。用于创建子图的plt.subplots例程接受sharex和sharey关键字参数，允许轴在所有子图或行或列之间共享。此设置会影响轴的比例和刻度。

另请参阅

Matplotlib 通过为subplots例程提供gridspec_kw关键字参数来支持更高级的布局。有关更多信息，请参阅matplotlib.gridspec的文档。

保存 Matplotlib 图

当您在交互式环境中工作，例如 IPython 控制台或 Jupyter 笔记本时，运行时显示图是完全正常的。但是，有很多情况下，直接将图存储到文件中而不是在屏幕上呈现会更合适。在本示例中，我们将看到如何将图直接保存到文件中，而不是在屏幕上显示。

准备工作

您需要要绘制的数据以及要存储输出的路径或文件对象。我们将结果存储在当前目录中的savingfigs.png中。在此示例中，我们将绘制以下数据：

x = np.arange(1, 5, 0.1)
y = x*x

如何做…

以下步骤显示了如何将 Matplotlib 图直接保存到文件：

1. 第一步是像往常一样创建图，并添加任何必要的标签、标题和注释。图将以其当前状态写入文件，因此应在保存之前进行对图的任何更改：

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_title("Graph of $y = x²$", usetex=True)
ax.set_xlabel("$x$", usetex=True)
ax.set_ylabel("$y$", usetex=True)

1. 然后，我们使用fig上的savefig方法将此图保存到文件。唯一必需的参数是要输出的路径或可以写入图形的文件对象。我们可以通过提供适当的关键字参数来调整输出格式的各种设置，例如分辨率。我们将输出图的每英寸点数（DPI）设置为300，这对于大多数应用程序来说是合理的分辨率：

fig.savefig("savingfigs.png", dpi=300)

Matplotlib 将根据给定文件的扩展名推断我们希望以便携式网络图形（PNG）格式保存图像。或者，可以通过提供关键字参数（使用format关键字）显式地提供格式，或者可以从配置文件中回退到默认格式。

它是如何工作的…

savefig方法选择适合输出格式的后端，然后以该格式呈现当前图。生成的图像数据将写入指定的路径或文件对象。如果您手动创建了Figure实例，则可以通过在该实例上调用savefig方法来实现相同的效果。

还有更多…

savefig例程接受许多额外的可选关键字参数来自定义输出图像。例如，可以使用dpi关键字指定图像的分辨率。本章中的图是通过将 Matplotlib 图保存到文件中生成的。

可用的输出格式包括 PNG、可缩放矢量图形（SVG）、PostScript（PS）、Encapsulated PostScript（EPS）和便携式文档格式（PDF）。如果安装了 Pillow 软件包，还可以保存为 JPEG 格式，但自 Matplotlib 3.1 版本以来就不再原生支持此功能。JPEG 图像还有其他自定义关键字参数，如quality和optimize。可以将图像元数据的字典传递给metadata关键字，在保存时将其写入图像元数据。

另请参阅

Matplotlib 网站上的示例库包括使用几种常见的 Python GUI 框架将 Matplotlib 图嵌入到图形用户界面（GUI）应用程序中的示例。

曲面和等高线图

Matplotlib 还可以以各种方式绘制三维数据。显示这种数据的两种常见选择是使用表面图或等高线图（类似于地图上的等高线）。在本示例中，我们将看到一种从三维数据绘制表面和绘制三维数据等高线的方法。

准备就绪

要绘制三维数据，需要将其排列成x、y和z分量的二维数组，其中x和y分量必须与z分量的形状相同。为了演示，我们将绘制对应于f(x, y) = x²y³函数的表面。

如何做…

我们想要在-2≤x≤2 和-1≤y≤1 范围内绘制f(x, y) = x²y³函数。第一项任务是创建一个适当的(x, y)对的网格，以便对该函数进行评估：

1. 首先使用np.linspace在这些范围内生成合理数量的点：

X = np.linspace(-2, 2)
Y = np.linspace(-1, 1)

1. 现在，我们需要创建一个网格来创建我们的z值。为此，我们使用np.meshgrid例程：

x, y = np.meshgrid(X, Y)

1. 现在，我们可以创建要绘制的z值，这些值保存了每个网格点上函数的值：

z = x**2 * y**3

1. 要绘制三维表面，我们需要加载一个 Matplotlib 工具箱mplot3d，它随 Matplotlib 包一起提供。这不会在代码中明确使用，但在幕后，它使三维绘图实用程序可用于 Matplotlib：

from mpl_toolkits import mplot3d

1. 接下来，我们创建一个新的图和一组三维坐标轴用于该图：

fig = plt.figure()
ax = fig.add_subplot(projection="3d")  # declare 3d plot

1. 现在，我们可以在这些坐标轴上调用plot_surface方法来绘制数据：

ax.plot_surface(x, y, z)

1. 为三维图添加轴标签非常重要，因为在显示的图上可能不清楚哪个轴是哪个：

ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$z$")

1. 此时我们还应该设置一个标题：

ax.set_title("Graph of the function $f(x) = x²y³$)

您可以使用plt.show例程在新窗口中显示图（如果您在 Python 中交互使用，而不是在 Jupyter 笔记本或 IPython 控制台上使用），或者使用plt.savefig将图保存到文件中。上述序列的结果如下所示：

图 2.6：使用默认设置使用 Matplotlib 生成的三维表面图

1. 等高线图不需要mplot3d工具包，在pyplot接口中有一个contour例程可以生成等高线图。但是，与通常的（二维）绘图例程不同，contour例程需要与plot_surface方法相同的参数。我们使用以下顺序生成绘图：

fig = plt.figure()  # Force a new figure
plt.contour(x, y, z)
plt.title("Contours of $f(x) = x²y³$")
plt.xlabel("$x$")
plt.ylabel("$y$")

结果显示在以下图中：

图 2.7：使用默认设置使用 Matplotlib 生成的等高线图

它是如何工作的…

mplot3d工具包提供了一个Axes3D对象，这是核心 Matplotlib 包中Axes对象的三维版本。当给定projection="3d"关键字参数时，这将被提供给Figure对象上的axes方法。通过在三维投影中在相邻点之间绘制四边形，可以获得表面图。这与用直线连接相邻点来近似二维曲线的方式相同。

plot_surface方法需要提供z值，这些值作为二维数组编码在(x, y)对的网格上的z值。我们创建了我们感兴趣的x和y值的范围，但是如果我们简单地在这些数组的对应值上评估我们的函数，我们将得到一条线上的z值，而不是整个网格上的值。相反，我们使用meshgrid例程，它接受两个X和Y数组，并从中创建一个网格，其中包含X和Y中所有可能的值的组合。输出是一对二维数组，我们可以在其上评估我们的函数。然后我们可以将这三个二维数组全部提供给plot_surface方法。

还有更多…

在前面的部分中描述的例程contour和plot_contour只适用于高度结构化的数据，其中x、y和z分量被排列成网格。不幸的是，现实生活中的数据很少有这么结构化的。在这种情况下，您需要在已知点之间执行某种插值，以近似均匀网格上的值，然后可以绘制出来。执行这种插值的常见方法是通过对(x, y)对的集合进行三角剖分，然后使用每个三角形顶点上的函数值来估计网格点上的值。幸运的是，Matplotlib 有一个方法可以执行所有这些步骤，然后绘制结果，这就是plot_trisurf例程。我们在这里简要解释一下如何使用它：

1. 为了说明plot_trisurf的用法，我们将从以下数据绘制表面和等高线：

x = np.array([ 0.19, -0.82, 0.8 , 0.95, 0.46, 0.71, 
     -0.86, -0.55,   0.75,-0.98, 0.55, -0.17, -0.89,
         -0.4 , 0.48, -0.09, 1., -0.03, -0.87, -0.43])
y = np.array([-0.25, -0.71, -0.88, 0.55, -0.88, 0.23, 
      0.18,-0.06, 0.95, 0.04, -0.59, -0.21, 0.14, 0.94, 
          0.51, 0.47, 0.79, 0.33, -0.85, 0.19])
z = np.array([-0.04, 0.44, -0.53, 0.4, -0.31, 0.13, 
      -0.12, 0.03, 0.53, -0.03, -0.25, 0.03, -0.1 , 
          -0.29, 0.19, -0.03, 0.58, -0.01, 0.55, -0.06])

1. 这次，我们将在同一图中绘制表面和等高线（近似），作为两个单独的子图。为此，我们向包含表面的子图提供projection="3d"关键字参数。我们在三维坐标轴上使用plot_trisurf方法绘制近似表面，并在二维坐标轴上使用tricontour方法绘制近似等高线：

fig = plt.figure(tight_layout=True)  # force new figure
ax1 = fig.add_subplot(1, 2, 1, projection="3d")  # 3d axes
ax1.plot_trisurf(x, y, z)
ax1.set_xlabel("$x$")
ax1.set_ylabel("$y$")
ax1.set_zlabel("$z$")
ax1.set_title("Approximate surface")

1. 现在，我们可以使用以下命令绘制三角剖分表面的等高线：

ax2 = fig.add_subplot(1, 2, 2)  # 2d axes
ax2.tricontour(x, y, z)
ax2.set_xlabel("$x$")
ax2.set_ylabel("$y$")
ax2.set_title("Approximate contours")

我们在图中包含tight_layout=True关键字参数，以避免稍后调用plt.tight_layout例程。结果如下所示：

图 2.8：使用三角剖分生成的近似表面和等高线图

除了表面绘图例程外，Axes3D对象还有一个用于简单三维绘图的plot（或plot3D）例程，其工作方式与通常的plot例程完全相同，但在三维坐标轴上。该方法还可用于在其中一个轴上绘制二维数据。

自定义三维图

等高线图可能会隐藏表示的表面的一些细节，因为它们只显示“高度”相似的地方，而不显示值是多少，甚至与周围的值相比如何。在地图上，这可以通过在特定等高线上打印高度来解决。表面图更具启发性，但是将三维对象投影到二维以在屏幕上显示可能会模糊一些细节。为了解决这些问题，我们可以自定义三维图（或等高线图）的外观，以增强图表并确保我们希望突出显示的细节清晰可见。最简单的方法是通过更改图表的颜色映射来实现这一点。

在这个示例中，我们将使用binary颜色映射的反转。

准备工作

我们将为以下函数生成表面图：

我们生成应该绘制的点，就像在前一个示例中一样：

X = np.linspace(-2, 2)
Y = np.linspace(-2, 2)
x, y = np.meshgrid(X, Y)
t = x**2 + y**2  # small efficiency
z = np.cos(2*np.pi*t)*np.exp(-t)

如何做…

Matplotlib 有许多内置的颜色映射，可以应用于图表。默认情况下，表面图是用根据光源进行着色的单一颜色绘制的（请参阅本示例的更多信息部分）。颜色映射可以显著改善图表的效果。以下步骤显示了如何向表面和等高线图添加颜色映射：

1. 首先，我们只需应用内置的颜色映射之一binary_r，通过向plot_surface例程提供cmap="binary_r"关键字参数来实现：

fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_surface(x, y, z, cmap="binary_r")
ax.set_title("Surface with colormap")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$z$")

结果是一个图（图 2.9），其中表面的颜色根据其值而变化，颜色映射的两端具有最极端的值——在本例中，z值越大，灰度越浅。请注意，下图中的不规则性是由网格中相对较少的点造成的：

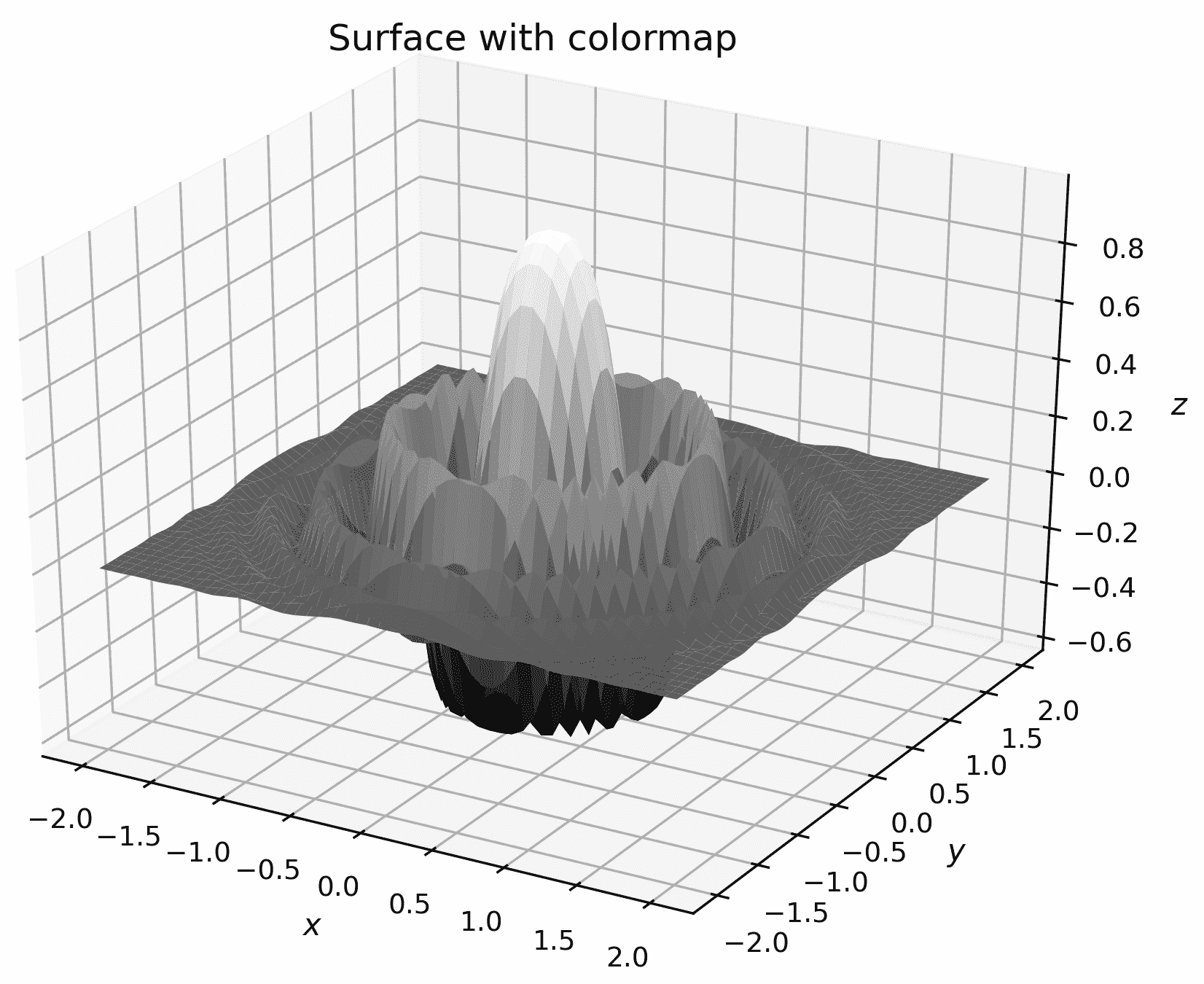
图 2.9：应用灰度颜色映射的表面图

颜色映射适用于表面绘图以外的其他绘图类型。特别是，颜色映射可以应用于等高线图，这有助于区分代表较高值和代表较低值的等高线。

1. 对于等高线图，更改颜色映射的方法是相同的；我们只需为cmap关键字参数指定一个值：

fig = plt.figure()
plt.contour(x, y, z, cmap="binary_r")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.title("Contour plot with colormap set")

上述代码的结果如下所示：

图 2.10：具有替代颜色映射设置的等高线图

图中较深的灰色阴影对应于 z 的较低值。

工作原理…

颜色映射通过根据比例尺分配 RGB 值来工作——颜色映射。首先，对值进行归一化，使其介于0和1之间，通常通过线性变换来实现，将最小值取为0，最大值取为1。然后将适当的颜色应用于表面绘图的每个面（或者在另一种类型的绘图中是线）。

Matplotlib 带有许多内置的颜色映射，可以通过简单地将名称传递给cmap关键字参数来应用。这些颜色映射的列表在文档中给出（matplotlib.org/tutorials/colors/colormaps.html），还有一个反转的变体，通过在所选颜色映射的名称后添加_r后缀来获得。

还有更多…

应用颜色映射中的归一化步骤是由Normalize类派生的对象执行的。Matplotlib 提供了许多标准的归一化例程，包括LogNorm和PowerNorm。当然，您也可以创建自己的Normalize子类来执行归一化。可以使用plot_surface或其他绘图函数的norm关键字添加替代Normalize子类。

对于更高级的用途，Matplotlib 提供了一个接口，用于使用光源创建自定义阴影。这是通过从matplotlib.colors包中导入LightSource类，然后使用该类的实例根据z值对表面元素进行着色来完成的。这是使用LightSource对象的shade方法完成的：

from matplotlib.colors import LightSource
light_source = LightSource(0, 45)  # angles of lightsource
cmap = plt.get_cmap("binary_r")
vals = light_source.shade(z, cmap)
surf = ax.plot_surface(x, y, z, facecolors=vals)

如果您希望了解更多关于这个工作原理的内容，可以在 Matplotlib 库中查看完整的示例。

进一步阅读

Matplotlib 包非常庞大，我们在这么短的篇幅内几乎无法充分展现它。文档中包含的细节远远超过了这里提供的内容。此外，还有一个大型的示例库（matplotlib.org/gallery/index.html#），其中包含了比本书中更多的包功能。

还有其他构建在 Matplotlib 之上的包，为特定应用程序提供了高级绘图方法。例如，Seaborn 库提供了用于可视化数据的例程（seaborn.pydata.org/）。

第四章：微积分和微分方程

在本章中，我们将讨论与微积分相关的各种主题。微积分是涉及微分和积分过程的数学分支。从几何上讲，函数的导数代表函数曲线的梯度，函数的积分代表函数曲线下方的面积。当然，这些特征只在某些情况下成立，但它们为本章提供了一个合理的基础。

我们首先来看一下简单函数类的微积分：多项式。在第一个示例中，我们创建一个表示多项式的类，并定义不同 iate 和积分多项式的方法。多项式很方便，因为多项式的导数或积分再次是多项式。然后，我们使用 SymPy 包对更一般的函数进行符号微分和积分。之后，我们看到使用 SciPy 包解方程的方法。接下来，我们将注意力转向数值积分（求积）和解微分方程。我们使用 SciPy 包来解常微分方程和常微分方程组，然后使用有限差分方案来解简单的偏微分方程。最后，我们使用快速傅里叶变换来处理嘈杂的信号并滤除噪音。

在本章中，我们将涵盖以下示例：

• 使用多项式和微积分

• 使用 SymPy 进行符号微分和积分

• 解方程

• 使用 SciPy 进行数值积分

• 使用数值方法解简单的微分方程

• 解微分方程组

• 使用数值方法解偏微分方程

• 使用离散傅里叶变换进行信号处理

技术要求

除了科学 Python 包 NumPy 和 SciPy 之外，我们还需要 SymPy 包。可以使用您喜欢的软件包管理器（如pip）来安装它：

          python3.8 -m pip install sympy

本章的代码可以在 GitHub 存储库的Chapter 03文件夹中找到，网址为github.com/PacktPublishing/Applying-Math-with-Python/tree/master/Chapter%2003。

查看以下视频以查看代码的实际操作：bit.ly/32HuH4X。

使用多项式和微积分

多项式是数学中最简单的函数之一，定义为一个求和：

x代表要替换的占位符，a[i]是一个数字。由于多项式很简单，它们提供了一个很好的方式来简要介绍微积分。微积分涉及函数的微分和积分。积分大致上是反微分，因为先积分然后微分会得到原始函数。

在本示例中，我们将定义一个表示多项式的简单类，并为该类编写方法以执行微分和积分。

准备工作

从几何上讲，通过微分得到的导数是函数的梯度，通过积分得到的积分是函数曲线与x轴之间的面积，考虑到曲线是在轴的上方还是下方。在实践中，微分和积分是通过一组规则和特别适用于多项式的标准结果来进行符号化处理。

本示例不需要额外的软件包。

如何做…

以下步骤描述了如何创建表示多项式的类，并为该类实现微分和积分方法：

1. 让我们首先定义一个简单的类来表示多项式：

class Polynomial:
    """Basic polynomial class"""

    def __init__(self, coeffs):
        self.coeffs = coeffs

    def __repr__(self):
        return f"Polynomial({repr(self.coeffs)})"

    def __call__(self, x):
        return sum(coeff*x**i for i, coeff 
                in enumerate(self.coeffs))

1. 现在我们已经为多项式定义了一个基本类，我们可以继续实现这个Polynomial类的微分和积分操作，以说明这些操作如何改变多项式。我们从微分开始。我们通过将当前系数列表中的每个元素（不包括第一个元素）相乘来生成新的系数。我们使用这个新的系数列表来创建一个新的Polynomial实例，然后返回：

    def differentiate(self):
        """Differentiate the polynomial and return the derivative"""
        coeffs = [i*c for i, c in enumerate(self.coeffs[1:], start=1)]
        return Polynomial(coeffs)

1. 要实现积分方法，我们需要创建一个包含由参数给出的新常数（转换为浮点数以保持一致性）的新系数列表。然后我们将旧系数除以它们在列表中的新位置，加到这个系数列表中：

    def integrate(self, constant=0):
        """Integrate the polynomial, returning the integral"""
        coeffs = [float(constant)] 
        coeffs += [c/i for i, c in enumerate(self.coeffs, start=1)]
        return Polynomial(coeffs)

1. 最后，为了确保这些方法按预期工作，我们应该用一个简单的案例测试这两种方法。我们可以使用一个非常简单的多项式来检查，比如x² - 2x + 1：

p = Polynomial([1, -2, 1])
p.differentiate()
# Polynomial([-2, 2])
p.integrate(constant=1)
# Polynomial([1.0, 1.0, -1.0, 0.3333333333])

工作原理…

多项式为我们提供了一个对微积分基本操作的简单介绍，但对于其他一般类的函数来说，构建 Python 类并不那么容易。也就是说，多项式非常有用，因为它们被很好地理解，也许更重要的是，对于多项式的微积分非常容易。对于变量x的幂，微分的规则是乘以幂并减少 1，因此x^n*变为*nx(n-1)。

积分更复杂，因为函数的积分不是唯一的。我们可以给积分加上任意常数并得到第二个积分。对于变量x的幂，积分的规则是将幂增加 1 并除以新的幂，因此x^n*变为*x(n+1)/(n+1)，所以要对多项式进行积分，我们将每个x的幂增加 1，并将相应的系数除以新的幂。

我们在这个食谱中定义的Polynomial类相当简单，但代表了核心思想。多项式由其系数唯一确定，我们可以将其存储为一组数值值的列表。微分和积分是我们可以对这个系数列表执行的操作。我们包括一个简单的__repr__方法来帮助显示Polynomial对象，以及一个__call__方法来促进在特定数值上的评估。这主要是为了演示多项式的评估方式。

多项式对于解决涉及评估计算昂贵函数的某些问题非常有用。对于这样的问题，我们有时可以使用某种多项式插值，其中我们将一个多项式“拟合”到另一个函数，然后利用多项式的性质来帮助解决原始问题。评估多项式比原始函数要“便宜”得多，因此这可能会大大提高速度。这通常是以一些精度为代价的。例如，辛普森法则用二次多项式逼近曲线下的面积，这些多项式是由三个连续网格点定义的间隔内的。每个二次多项式下面的面积可以通过积分轻松计算。

还有更多…

多项式在计算编程中扮演的角色远不止是展示微分和积分的效果。因此，NumPy 包中提供了一个更丰富的Polynomial类，numpy.polynomial。NumPy 的Polynomial类和各种派生子类在各种数值问题中都很有用，并支持算术运算以及其他方法。特别是，有用于将多项式拟合到数据集合的方法。

NumPy 还提供了从Polynomial派生的类，表示各种特殊类型的多项式。例如，Legendre类表示一种特定的多项式系统，称为Legendre多项式。Legendre 多项式是为满足*-1 ≤ x ≤ 1的x*定义的，并且形成一个正交系统，这对于诸如数值积分和有限元方法解决偏微分方程等应用非常重要。Legendre 多项式使用递归关系定义。我们定义

对于每个n ≥ 2，我们定义第n个 Legendre 多项式满足递推关系，

还有一些所谓的正交（系统的）多项式，包括Laguerre多项式*，Chebyshev 多项式和Hermite 多项式。

参见

微积分在数学文本中有很好的文档记录，有许多教科书涵盖了从基本方法到深层理论的内容。正交多项式系统在数值分析文本中也有很好的文档记录。

使用 SymPy 进行符号微分和积分

在某些时候，您可能需要区分一个不是简单多项式的函数，并且可能需要以某种自动化的方式来做这件事，例如，如果您正在编写教育软件。Python 科学堆栈包括一个名为 SymPy 的软件包，它允许我们在 Python 中创建和操作符号数学表达式。特别是，SymPy 可以执行符号函数的微分和积分，就像数学家一样。

在这个示例中，我们将创建一个符号函数，然后使用 SymPy 库对这个函数进行微分和积分。

准备工作

与其他一些科学 Python 软件包不同，文献中似乎没有一个标准的别名来导入 SymPy。相反，文档在几个地方使用了星号导入，这与 PEP8 风格指南不一致。这可能是为了使数学表达更自然。我们将简单地按照其名称sympy导入模块，以避免与scipy软件包的标准缩写sp混淆（这也是sympy的自然选择）：

import sympy

在这个示例中，我们将定义一个表示函数的符号表达式

如何做…

使用 SymPy 软件包进行符号微分和积分（就像您手工操作一样）非常容易。按照以下步骤来看看它是如何完成的：

1. 一旦导入了 SymPy，我们就定义将出现在我们的表达式中的符号。这是一个没有特定值的 Python 对象，就像数学变量一样，但可以在公式和表达式中表示许多不同的值。对于这个示例，我们只需要定义一个符号用于x，因为除此之外我们只需要常数（文字）符号和函数。我们使用sympy中的symbols例程来定义一个新符号。为了保持符号简单，我们将这个新符号命名为x：

x = sympy.symbols('x')

1. 使用symbols函数定义的符号支持所有算术运算，因此我们可以直接使用我们刚刚定义的符号x构造表达式：

f = (x**2 - 2*x)*sympy.exp(3 - x)

1. 现在我们可以使用 SymPy 的符号微积分能力来计算f的导数，即对f进行微分。我们使用sympy中的diff例程来完成这个操作，它对指定的符号进行符号表达式微分，并返回导数的表达式。这通常不是以最简形式表达的，因此我们使用sympy.simplify例程来简化结果：

fp = sympy.simplify(sympy.diff(f))  # (x*(2 - x) + 2*x - 2)
                                                       *exp(3 - x)

1. 我们可以通过以下方式检查使用 SymPy 进行符号微分的结果是否正确，与手工计算的导数相比，定义为 SymPy 表达式：

fp2 = (2*x - 2)*sympy.exp(3 - x) - (x**2 - 2*x)*sympy.exp(3 - x)

1. SymPy 相等性测试两个表达式是否相等，但不测试它们是否在符号上等价。因此，我们必须首先简化我们希望测试的两个语句的差异，并测试是否等于0：

sympy.simplify(fp2 - fp) == 0  # True

1. 我们可以使用 SymPy 通过integrate函数对函数f进行积分。还可以通过将其作为第二个可选参数提供来提供要执行积分的符号：

F = sympy.integrate(f, x)  # -x**2*exp(3 - x)

它是如何工作的…

SymPy 定义了表示某些类型表达式的各种类。例如，由Symbol类表示的符号是原子表达式的例子。表达式是以与 Python 从源代码构建抽象语法树的方式构建起来的。然后可以使用方法和标准算术运算来操作这些表达式对象。

SymPy 还定义了可以在Symbol对象上操作以创建符号表达式的标准数学函数。最重要的特性是能够执行符号微积分 - 而不是我们在本章剩余部分中探索的数值微积分 - 并给出对微积分问题的精确（有时称为解析）解决方案。

SymPy 软件包中的diff例程对这些符号表达式进行微分。这个例程的结果通常不是最简形式，这就是为什么我们在配方中使用简化例程来简化导数的原因。integrate例程用给定的符号对scipy表达式进行符号积分。（diff例程还接受一个符号参数，用于指定微分的符号。）这将返回一个其导数为原始表达式的表达式。这个例程不会添加积分常数，这在手工积分时是一个好的做法。

还有更多…

SymPy 可以做的远不止简单的代数和微积分。它有各种数学领域的子模块，如数论、几何和其他离散数学（如组合数学）。

SymPy 表达式（和函数）可以构建成 Python 函数，可以应用于 NumPy 数组。这是使用sympy.utilities模块中的lambdify例程完成的。这将 SymPy 表达式转换为使用 SymPy 标准函数的 NumPy 等价函数来数值评估表达式。结果类似于定义 Python Lambda，因此得名。例如，我们可以使用这个例程将这个配方中的函数和导数转换为 Python 函数：

from sympy.utilities import lambdify
lam_f = lambdify(x, f)
lam_fp = lambdify(x, fp)

lambdify例程接受两个参数。第一个是要提供的变量，上一个代码块中的x，第二个是在调用此函数时要评估的表达式。例如，我们可以评估之前定义的 lambdified SymPy 表达式，就好像它们是普通的 Python 函数一样：

lam_f(4)  # 2.9430355293715387
lam_fp(7)  # -0.4212596944408861

我们甚至可以在 NumPy 数组上评估这些 lambdified 表达式：

lam_f(np.array([0, 1, 2]))  # array([ 0\. , -7.3890561, 0\. ])

lambdify例程使用 Python 的exec例程来执行代码，因此不应该与未经过消毒的输入一起使用。

解方程

许多数学问题最终归结为解形式为f(x) = 0 的方程，其中f是单变量函数。在这里，我们试图找到一个使方程成立的x的值。使方程成立的x的值有时被称为方程的根。有许多算法可以找到这种形式的方程的解。在这个配方中，我们将使用牛顿-拉弗森和弦截法来解决形式为f(x) = 0 的方程。

牛顿-拉弗森方法（牛顿法）和弦截法是良好的标准根查找算法，几乎可以应用于任何情况。这些是迭代方法，从一个根的近似值开始，并迭代改进这个近似值，直到它在给定的容差范围内。

为了演示这些技术，我们将使用使用 SymPy 进行符号计算配方中定义的函数

它对所有实数x都有定义，并且恰好有两个根，一个在x=0，另一个在x=2。

准备工作

SciPy 包含用于解方程的例程（以及许多其他内容）。根查找例程可以在scipy包的optimize模块中找到。

如果你的方程不是形式上的f(x) = 0，那么你需要重新排列它，使其成为这种情况。这通常不太困难，只需要将右侧的任何项移到左侧即可。例如，如果你希望找到函数的不动点，也就是当g(x)= x时，我们会将方法应用于由f(x) =g(x)*- x.*给出的相关函数。

如何操作…

optimize包提供了用于数值根查找的例程。以下说明描述了如何使用该模块中的newton例程：

1. optimize模块没有列在scipy命名空间中，所以你必须单独导入它：

from scipy import optimize

1. 然后我们必须在 Python 中定义这个函数及其导数：

from math import exp

def f(x):
    return x*(x - 2)*exp(3 - x)

1. 这个函数的导数在前一个配方中被计算出来：

def fp(x):
    return -(x**2 - 4*x + 2)*exp(3 - x)

1. 对于牛顿-拉弗森和割线法，我们使用optimize中的newton例程。割线法和牛顿-拉弗森法都需要函数和第一个参数以及第一个近似值x0作为第二个参数。要使用牛顿-拉弗森法，我们必须提供f的导数，使用fprime关键字参数：

optimize.newton(f, 1, fprime=fp) # Using the Newton-Raphson method
# 2.0

1. 使用割线法时，只需要函数，但是我们必须提供根的前两个近似值；第二个作为x1关键字参数提供：

optimize.newton(f, 1., x1=1.5) # Using x1 = 1.5 and the secant method
# 1.9999999999999862

牛顿-拉弗森法和割线法都不能保证收敛到根。完全有可能方法的迭代只是在一些点之间循环（周期性）或者波动剧烈（混沌）。

工作原理…

对于具有导数f’(x)和初始近似值x[0]的函数f(x)，牛顿-拉弗森方法使用以下公式进行迭代定义

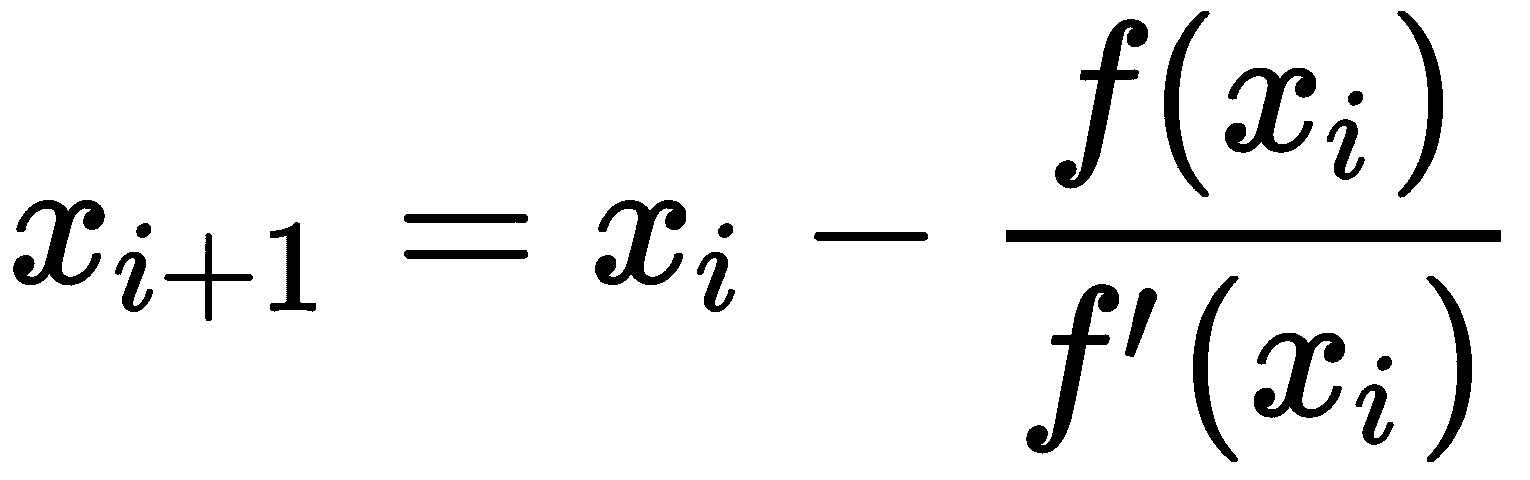
对于每个整数i ≥0。从几何上讲，这个公式是通过考虑梯度的负方向（所以函数是递减的）如果f(x[i])>0或正方向（所以函数是递增的）如果f(x[i]) <o。

割线法基于牛顿-拉弗森法，但是用近似值替换了一阶导数

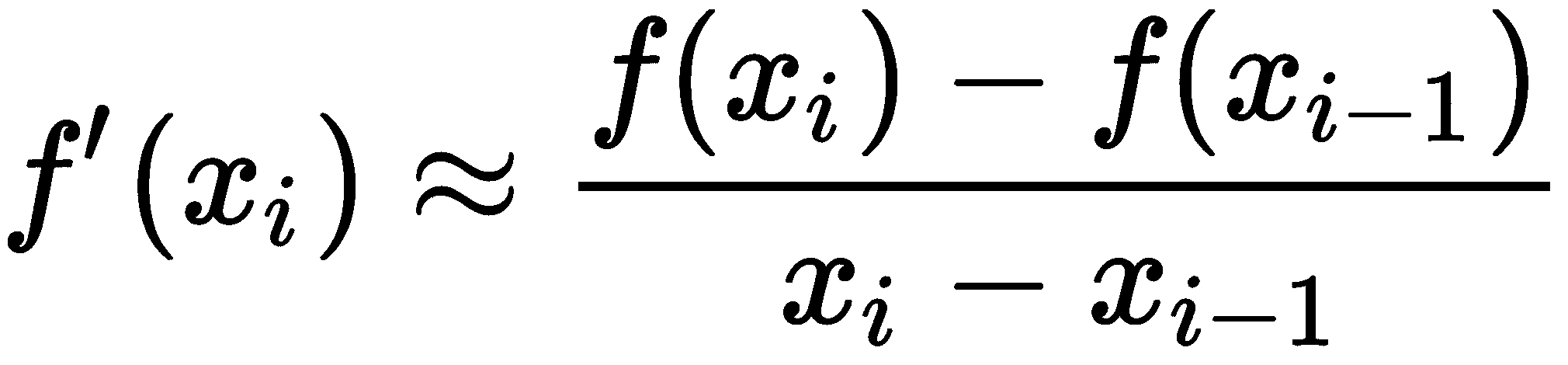
当x[i]-x[i-1]足够小时，这意味着方法正在收敛，这是一个很好的近似值。不需要函数f的导数的代价是我们需要一个额外的初始猜测来启动方法。该方法的公式如下

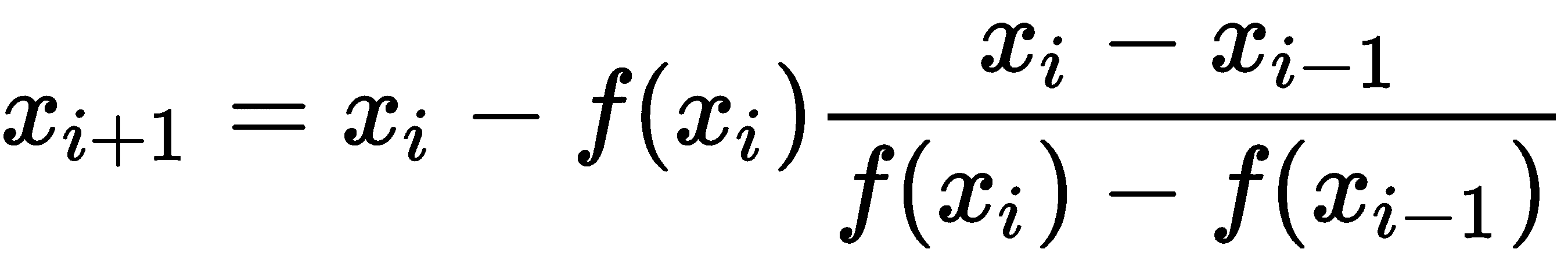
一般来说，如果任一方法得到一个足够接近根的初始猜测（割线法的猜测），那么该方法将收敛于该根。牛顿-拉弗森法在迭代中导数为零时也可能失败，此时公式未被很好地定义。

还有更多…

本配方中提到的方法是通用方法，但在某些情况下可能有更快或更准确的方法。广义上讲，根查找算法分为两类：在每次迭代中使用函数梯度信息的算法（牛顿-拉弗森、割线、Halley）和需要根位置的界限的算法（二分法、regula-falsi、Brent）。到目前为止讨论的算法属于第一类，虽然通常相当快，但可能无法收敛。

第二种算法是已知根存在于指定区间内的算法a ≤**x ≤b。我们可以通过检查f(a)和f(b)是否有不同的符号来检查根是否在这样的区间内，也就是说，f(a) <0<f(b)或f(b) <0<f(a)其中一个为真。（当然，前提是函数是连续的，在实践中往往是这样。）这种类型的最基本算法是二分法算法，它重复地将区间二分，直到找到根的足够好的近似值。基本前提是在a和b之间分割区间，并选择函数改变符号的区间。该算法重复，直到区间非常小。以下是 Python 中此算法的基本实现：

from math import copysign

def bisect(f, a, b, tol=1e-5):
    """Bisection method for root finding"""
    fa, fb = f(a), f(b)
    assert not copysign(fa, fb) == fa, "Function must change signs"
    while (b - a) > tol:
        m = (b - a)/2 # mid point of the interval
        fm = f(m)
        if fm == 0:
            return m
        if copysign(fm, fa) == fm: # fa and fm have the same sign
            a = m
            fa = fm
        else: # fb and fm have the same sign
            b = m
        return a

该方法保证收敛，因为在每一步中，距离b-a减半。但是，可能需要比牛顿-拉弗森或割线法更多的迭代次数。optimize中也可以找到二分法的版本。这个版本是用 C 实现的，比这里呈现的版本要高效得多，但是在大多数情况下，二分法不是最快的方法。

Brent 的方法是对二分法的改进，在optimize模块中作为brentq可用。它使用二分和插值的组合来快速找到方程的根：

optimize.brentq(f, 1.0, 3.0)  # 1.9999999999998792

重要的是要注意，涉及括号（二分法、regula-falsi、Brent）的技术不能用于找到复变量的根函数，而不使用括号（Newton、割线、Halley）的技术可以。

使用 SciPy 进行数值积分

积分可以解释为曲线与x轴之间的区域，根据这个区域是在轴的上方还是下方进行标记。有些积分无法直接使用符号方法计算，而必须进行数值近似。其中一个经典例子是高斯误差函数，在第一章的基本数学函数部分中提到。这是由以下公式定义的

这里出现的积分也无法通过符号方法计算。

在本示例中，我们将看到如何使用 SciPy 包中的数值积分例程来计算函数的积分。

准备工作

我们使用scipy.integrate模块，其中包含几个用于计算数值积分的例程。我们将此模块导入如下：

from scipy import integrate

操作步骤…

以下步骤描述了如何使用 SciPy 进行数值积分：

1. 我们评估出现在误差函数定义中的积分在x = 1处的值。为此，我们需要在 Python 中定义被积函数（出现在积分内部）：

def erf_integrand(t):
    return np.exp(-t**2)

scipy.integrate中有两个主要例程用于执行数值积分（求积），可以使用。第一个是quad函数，它使用 QUADPACK 执行积分，第二个是quadrature。

1. quad例程是一个通用的积分工具。它期望三个参数，即要积分的函数（erf_integrand），下限（-1.0）和上限（1.0）：

val_quad, err_quad = integrate.quad(erf_integrand, -1.0, 1.0)
# (1.493648265624854, 1.6582826951881447e-14)

第一个返回值是积分的值，第二个是误差的估计。

1. 使用quadrature例程重复计算，我们得到以下结果。参数与quad例程相同：

val_quadr, err_quadr = integrate.quadrature(erf_integrand, -1.0,
    1.0)
# (1.4936482656450039, 7.459897144457273e-10)

输出与代码的格式相同，先是积分的值，然后是误差的估计。请注意，quadrature例程的误差更大。这是因为一旦估计的误差低于给定的容差，方法就会终止，当调用例程时可以修改这个容差。

工作原理…

大多数数值积分技术都遵循相同的基本过程。首先，我们选择积分区域中的点x[i]，对于i = 1, 2,…, n，然后使用这些值和值f(x[i])来近似积分。例如，使用梯形法则，我们通过以下方式近似积分

其中a < x[1]< x[2]< … < x[n-1]< b，h是相邻x[i]值之间的（公共）差异，包括端点a和b。这可以在 Python 中实现如下：

def trapezium(func, a, b, n_steps):
    """Estimate an integral using the trapezium rule"""
    h = (b - a) / n_steps
    x_vals = np.arange(a + h, b, h) 
    y_vals = func(x_vals)
    return 0.5*h*(func(a) + func(b) + 2.*np.sum(y_vals))

quad和quadrature使用的算法比这复杂得多。使用这个函数来近似使用trapezium积分erf_integrand的积分得到的结果是 1.4936463036001209，这与quad和quadrature例程的近似结果在 5 位小数的情况下是一致的。

quadrature例程使用固定容差的高斯积分，而quad例程使用 Fortran 库 QUADPACK 例程中实现的自适应算法。对两个例程进行计时，我们发现对于配方中描述的问题，quad例程大约比quadrature例程快 5 倍。quad例程在大约 27 微秒内执行，平均执行 1 百万次，而quadrature例程在大约 134 微秒内执行。（您的结果可能会因系统而异。）

还有更多…

本节提到的例程需要知道被积函数，但情况并非总是如此。相反，可能是我们知道一些(x,y)对，其中y = f(x)，但我们不知道要在额外点上评估的函数f。在这种情况下，我们可以使用scipy.integrate中的采样积分技术之一。如果已知点的数量非常大，并且所有点都是等间距的，我们可以使用 Romberg 积分来很好地近似积分。为此，我们使用romb例程。否则，我们可以使用梯形法则的变体（如上所述）使用trapz例程，或者使用simps例程使用辛普森法则。

数值解简单微分方程

微分方程出现在一个数量根据给定关系演变的情况中，通常是随着时间的推移。它们在工程和物理学中非常常见，并且自然地出现。一个经典的（非常简单）微分方程的例子是牛顿提出的冷却定律。物体的温度以与当前温度成比例的速率冷却。从数学上讲，这意味着我们可以写出物体在时间t > 0时的温度T的导数，使用微分方程

常数k是一个确定冷却速率的正常数。这个微分方程可以通过首先“分离变量”，然后积分和重新排列来解析地解决。执行完这个过程后，我们得到了一般解

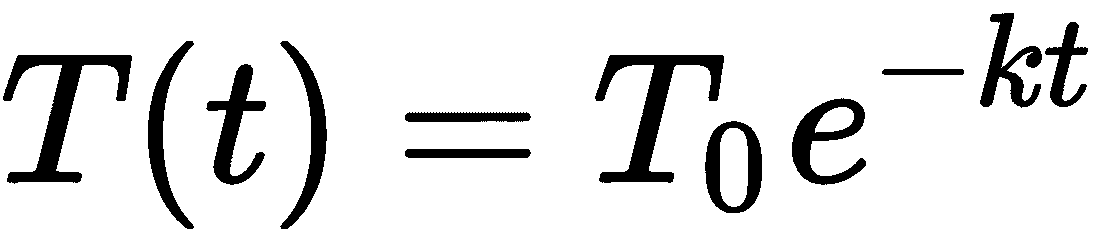
其中*T[0]*是初始温度。

在这个配方中，我们将使用 SciPy 的solve_ivp例程数值地解决一个简单的常微分方程。

准备工作

我们将演示在 Python 中使用先前描述的冷却方程数值地解决微分方程的技术，因为在这种情况下我们可以计算真实解。我们将初始温度取为T[0]= 50和k = 0.2。让我们也找出t值在 0 到 5 之间的解。

一般（一阶）微分方程的形式为

其中f是t（自变量）和y（因变量）的某个函数。在这个公式中，T是因变量，f(t, T) = -kt。SciPy 包中用于解决微分方程的例程需要函数f和初始值y[0][以及我们需要计算解的t值范围。要开始，我们需要在 Python 中定义我们的函数f并创建变量y[0][和t范围，准备提供给 SciPy 例程：]]

def f(t, y):
    return -0.2*y

t_range = (0, 5)

接下来，我们需要定义应从中找到解的初始条件。出于技术原因，初始y值必须指定为一维 NumPy 数组：

T0 = np.array([50.])

由于在这种情况下，我们已经知道真实解，我们也可以在 Python 中定义这个解，以便与我们将计算的数值解进行比较：

def true_solution(t):
    return 50.*np.exp(-0.2*t)

如何做到…

按照以下步骤数值求解微分方程并绘制解以及误差：

1. 我们使用 SciPy 中的integrate模块中的solve_ivp例程来数值求解微分方程。我们添加了一个最大步长的参数，值为0.1，这样解就可以在合理数量的点上计算出来：

sol = integrate.solve_ivp(f, t_range, T0, max_step=0.1)

1. 接下来，我们从solve_ivp方法返回的sol对象中提取解的值：

t_vals = sol.t
T_vals = sol.y[0, :]

1. 接下来，我们按如下方式在一组坐标轴上绘制解。由于我们还将在同一图中绘制近似误差，我们使用subplots例程创建两个子图：

fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True)
ax1.plot(t_vals, T_vals)
ax1.set_xlabel("$t$")
ax1.set_ylabel("$T$")
ax1.set_title("Solution of the cooling equation")

这在图 3.1的左侧显示了解决方案的图。

1. 为此，我们需要计算从solve_ivp例程中获得的点处的真实解，然后计算真实解和近似解之间的差的绝对值：

err = np.abs(T_vals - true_solution(t_vals))

1. 最后，在图 3.1的右侧，我们使用y轴上的对数刻度绘制近似误差。然后，我们可以使用semilogy绘图命令在右侧使用对数刻度y轴，就像我们在第二章中看到的那样，使用 Matplotlib 进行数学绘图：

ax2.semilogy(t_vals, err)
ax2.set_xlabel("$t$")
ax2.set_ylabel("Error")
ax2.set_title("Error in approximation")

图 3.1中的左侧图显示随时间降低的温度，而右侧图显示随着我们远离初始条件给出的已知值，误差增加：

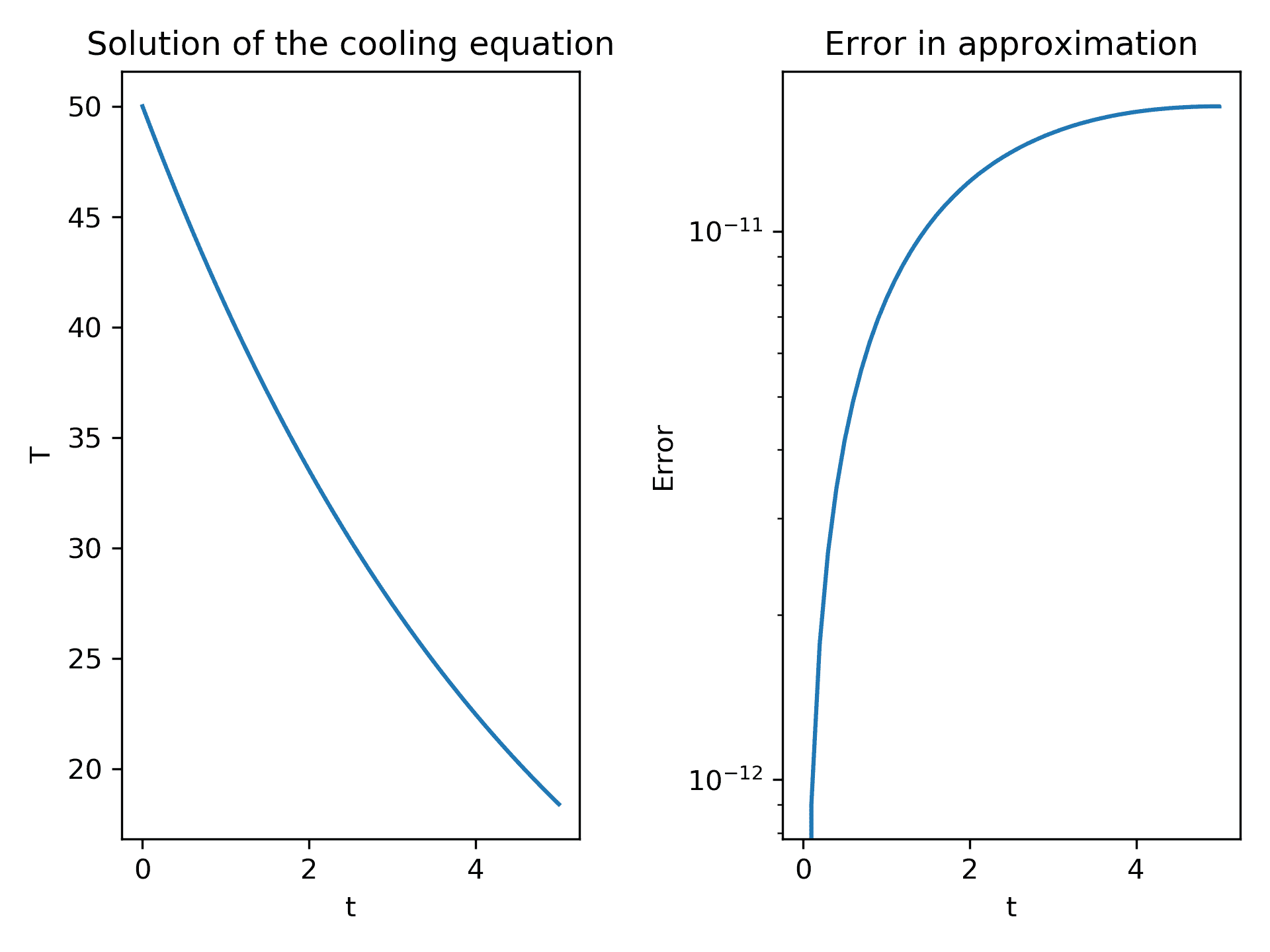图 3.1：使用默认设置使用 solve_ivp 例程获得冷却方程的数值解的绘图

它是如何工作的…

解决微分方程的大多数方法都是“时间步进”方法。(t[i], y[i])对是通过采取小的t步骤并逼近函数y的值来生成的。这可能最好地通过欧拉方法来说明，这是最基本的时间步进方法。固定一个小的步长h > 0，我们使用以下公式在第i步形成近似值

从已知的初始值*y[0]*开始。我们可以轻松地编写一个执行欧拉方法的 Python 例程如下（当然，实现欧拉方法有许多不同的方法；这是一个非常简单的例子）：

1. 首先，通过创建将存储我们将返回的t值和y值的列表来设置方法：

def euler(func, t_range, y0, step_size):
    """Solve a differential equation using Euler's method"""
    t = [t_range[0]]
    y = [y0]
    i = 0

1. 欧拉方法一直持续到我们达到t范围的末尾。在这里，我们使用while循环来实现这一点。循环的主体非常简单；我们首先递增计数器i，然后将新的t和y值附加到它们各自的列表中。

    while t[i] < t_range[1]:
        i += 1
        t.append(t[i-1] + step_size)  # step t
        y.append(y[i-1] + step_size*func(t[i-1], y[i-1]))  # step y
    return t, y

solve_ivp例程默认使用龙格-库塔-费尔伯格（RK45）方法，该方法能够自适应步长，以确保近似误差保持在给定的容差范围内。这个例程期望提供三个位置参数：函数f，应找到解的t范围，以及初始y值（在我们的例子中为T[0]）。可以提供可选参数来更改求解器、要计算的点数以及其他几个设置。

传递给solve_ivp例程的函数必须有两个参数，就像准备就绪部分中描述的一般微分方程一样。函数可以有额外的参数，可以使用args关键字为solve_ivp例程提供这些参数，但这些参数必须位于两个必要参数之后。将我们之前定义的euler例程与步长为 0.1 的solve_ivp例程进行比较，我们发现solve_ivp解的最大真实误差在 10^(-6)数量级，而euler解只能达到 31 的误差。euler例程是有效的，但步长太大，无法克服累积误差。

solve_ivp例程返回一个存储已计算解的信息的解对象。这里最重要的是t和y属性，它们包含计算解的t值和解y本身。我们使用这些值来绘制我们计算的解。y值存储在形状为(n, N)的 NumPy 数组中，其中n是方程的分量数（这里是 1），N是计算的点数。sol中的y值存储在一个二维数组中，在这种情况下有 1 行和许多列。我们使用切片y[0, :]来提取这个第一行作为一维数组，可以用来在步骤 4中绘制解。

我们使用对数缩放的y轴来绘制误差，因为有趣的是数量级。在非缩放的y轴上绘制它会得到一条非常靠近x轴的线，这不会显示出随着t值的变化误差的增加。对数缩放的y轴清楚地显示了这种增加。

还有更多…

solve_ivp例程是微分方程的多个求解器的便捷接口，默认为龙格-库塔-费尔伯格（RK45）方法。不同的求解器有不同的优势，但 RK45 方法是一个很好的通用求解器。

另请参阅

有关如何在 Matplotlib 中的图中添加子图的更详细说明，请参阅第二章中的添加子图示例，使用 Matplotlib 进行数学绘图。

解决微分方程系统

微分方程有时出现在由两个或更多相互关联的微分方程组成的系统中。一个经典的例子是竞争物种的简单模型。这是一个由以下方程给出的竞争物种的简单模型，标记为P（猎物）和W（捕食者）：*

*

第一个方程规定了猎物物种P的增长，如果没有任何捕食者，它将是指数增长。第二个方程规定了捕食者物种W的增长，如果没有任何猎物，它将是指数衰减。当然，这两个方程是耦合的；每种群体的变化都取决于两种群体。捕食者以与两种群体的乘积成比例的速率消耗猎物，并且捕食者以与猎物相对丰富度成比例的速率增长（再次是两种群体的乘积）。

在本示例中，我们将分析一个简单的微分方程系统，并使用 SciPy 的integrate模块来获得近似解。

准备就绪

使用 Python 解决常微分方程组的工具与解决单个方程的工具相同。我们再次使用 SciPy 中的integrate模块中的solve_ivp例程。然而，这只会给我们一个在给定起始种群下随时间预测的演变。因此，我们还将使用 Matplotlib 中的一些绘图工具来更好地理解这种演变。

如何做到…

以下步骤介绍了如何分析一个简单的常微分方程组：

1. 我们的第一个任务是定义一个包含方程组的函数。这个函数需要接受两个参数，就像单个方程一样，除了依赖变量y（在Solving simple differential equations numerically配方中的符号）现在将是一个包含与方程数量相同的元素的数组。在这里，将有两个元素。在这个配方中，我们需要的函数如下：

def predator_prey_system(t, y):
    return np.array([5*y[0] - 0.1*y[0]*y[1], 0.1*y[1]*y[0] -
       6*y[1]])

1. 现在我们已经在 Python 中定义了系统，我们可以使用 Matplotlib 中的quiver例程来生成一个图表，描述种群将如何演变——由方程给出——在许多起始种群中。我们首先设置一个网格点，我们将在这些点上绘制这种演变。选择相对较少的点数作为quiver例程的一个好主意，否则在图表中很难看到细节。对于这个例子，我们绘制种群值在 0 到 100 之间：

p = np.linspace(0, 100, 25)
w = np.linspace(0, 100, 25)
P, W = np.meshgrid(p, w)

1. 现在，我们计算每对这些点的系统值。请注意，系统中的任何一个方程都不是时间相关的（它们是自治的）；时间变量t在计算中并不重要。我们为t参数提供值0：

dp, dw = predator_prey_system(0, np.array([P, W]))

1. 现在变量dp和dw分别保存了种群P和W在我们的网格中每个点开始时将如何演变的“方向”。我们可以使用matplotlib.pyplot中的quiver例程一起绘制这些方向：

fig, ax = plt.subplots()
ax.quiver(P, W, dp, dw)
ax.set_title("Population dynamics for two competing species")
ax.set_xlabel("P")
ax.set_ylabel("W")

现在绘制这些命令的结果给出了图 3.2，它给出了解决方案演变的“全局”图像：

图 3.2：显示由常微分方程组模拟的两个竞争物种的种群动态的 quiver 图

为了更具体地理解解决方案，我们需要一些初始条件，这样我们就可以使用前面配方中描述的solve_ivp例程。

1. 由于我们有两个方程，我们的初始条件将有两个值。（回想一下，在Solving simple differential equations numerically配方中，我们看到提供给solve_ivp的初始条件需要是一个 NumPy 数组。）让我们考虑初始值P(0) = 85和W(0) = 40。我们在一个 NumPy 数组中定义这些值，小心地按正确的顺序放置它们：

initial_conditions = np.array([85, 40])

1. 现在我们可以使用scipy.integrate模块中的solve_ivp。我们需要提供max_step关键字参数，以确保我们在解决方案中有足够的点来得到平滑的解曲线：

from scipy import integrate
sol = integrate.solve_ivp(predator_prey_system, (0., 5.),
   initial_conditions, max_step=0.01)

1. 让我们在现有的图上绘制这个解，以展示这个特定解与我们已经生成的方向图之间的关系。我们同时也绘制初始条件：

ax.plot(initial_conditions[0], initial_conditions[1], "ko")
ax.plot(sol.y[0, :], sol.y[1, :], "k", linewidth=0.5)

这个结果显示在图 3.3中：

图 3.3：在显示一般行为的 quiver 图上绘制的解轨迹

它是如何工作的…

用于一组常微分方程的方法与单个常微分方程完全相同。我们首先将方程组写成一个单一的向量微分方程，

然后可以使用时间步进方法来解决，就好像y是一个简单的标量值一样。

使用quiver例程在平面上绘制方向箭头的技术是学习系统如何从给定状态演变的一种快速简单的方法。函数的导数代表曲线的梯度（x，u（x）），因此微分方程描述了解决方案函数在位置y和时间t的梯度。一组方程描述了在给定位置y和时间t的单独解决方案函数的梯度。当然，位置现在是一个二维点，所以当我们在一个点上绘制梯度时，我们将其表示为从该点开始的箭头，指向梯度的方向。箭头的长度表示梯度的大小；箭头越长，解决方案曲线在该方向上移动得越“快”。

当我们在这个方向场上绘制解的轨迹时，我们可以看到曲线（从该点开始）遵循箭头指示的方向。解的轨迹所显示的行为是一个极限环，其中每个变量的解都是周期性的，因为两种物种的人口增长或下降。如果我们将每个人口随时间的变化绘制成图，从图 3.4中可以看出，这种行为描述可能更清晰。从图 3.3中并不立即明显的是解的轨迹循环几次，但这在图 3.4中清楚地显示出来：

图 3.4：人口P和W随时间的变化图。两种人口都表现出周期性行为。

还有更多…

通过在变量之间绘制相空间（平面）分析系统的普通微分方程组的技术称为相空间（平面）分析。在这个示例中，我们使用quiver绘图例程快速生成了微分方程系统的相平面的近似值。通过分析微分方程系统的相平面，我们可以识别解的不同局部和全局特征，如极限环。

数值求解偏微分方程

偏微分方程是涉及函数在两个或多个变量中的偏导数的微分方程，而不是仅涉及单个变量的普通导数。偏微分方程是一个广泛的主题，可以轻松填满一系列书籍。偏微分方程的典型例子是（一维）热方程。

其中α是一个正常数，f（t，x）是一个函数。这个偏微分方程的解是一个函数u（t，x），它表示了在给定时间t>0 时，占据x范围 0≤x≤L的杆的温度。为了简单起见，我们将取f（t，x）=0，这相当于说系统没有加热/冷却，α=1，L=2。在实践中，我们可以重新调整问题来修复常数α，所以这不是一个限制性的问题。在这个例子中，我们将使用边界条件

这相当于说杆的两端保持在恒定温度 0。我们还将使用初始温度剖面

这个初始温度剖面描述了 0 和 2 之间的值之间的平滑曲线，峰值为 3，这可能是将杆在中心加热到 3 度的结果。

我们将使用一种称为有限差分的方法，将杆分成若干相等的段，并将时间范围分成若干离散步骤。然后我们计算每个段和每个时间步长的解的近似值。

在这个示例中，我们将使用有限差分来解一个简单的偏微分方程。

准备工作

对于这个示例，我们将需要 NumPy 包和 Matplotlib 包，通常导入为np和plt。我们还需要从mpl_toolkits导入mplot3d模块，因为我们将生成一个 3D 图：

from mpl_toolkits import mplot3d

我们还需要一些来自 SciPy 包的模块。

如何做…

在接下来的步骤中，我们将通过有限差分来解决热方程：

1. 首先创建代表系统物理约束的变量：杆的范围和α的值：

alpha = 1
x0 = 0 # Left hand x limit
xL = 2 # Right hand x limit

1. 我们首先将x范围分成N个相等的间隔—我们在这个例子中取N = 10*—使用N+1个点。我们可以使用 NumPy 中的linspace例程生成这些点。我们还需要每个间隔的公共长度h:

N = 10
x = np.linspace(x0, xL, N+1)
h = (xL - x0) / N

1. 接下来，我们需要设置时间方向上的步长。我们在这里采取了稍微不同的方法；我们设置时间步长k和步数（隐含地假设我们从时间 0 开始）：

k = 0.01
steps = 100
t = np.array([i*k for i in range(steps+1)])

1. 为了使方法正常运行，我们必须满足：

否则系统可能变得不稳定。我们将左侧存储在一个变量中，以便在步骤 4中使用，并使用断言来检查这个不等式是否成立：

r = alpha*k / h**2
assert r < 0.5, f"Must have r < 0.5, currently r={r}"

1. 现在我们可以构建一个矩阵，其中包含来自有限差分方案的系数。为此，我们使用scipy.sparse模块中的diags例程创建一个稀疏的三对角矩阵：

from scipy import sparse
diag = [1, *(1-2*r for _ in range(N-1)), 1]
abv_diag = [0, *(r for _ in range(N-1))]
blw_diag = [*(r for _ in range(N-1)), 0]

A = sparse.diags([blw_diag, diag, abv_diag], (-1, 0, 1), shape=(N+1,
      N+1), dtype=np.float64, format="csr")

1. 接下来，我们创建一个空白矩阵来保存解决方案：

u = np.zeros((steps+1, N+1), dtype=np.float64)

1. 我们需要将初始配置添加到第一行。这样做的最佳方法是创建一个保存初始配置的函数，并将在刚刚创建的矩阵u上的x数组上评估这个函数的结果：

def initial_profile(x):
    return 3*np.sin(np.pi*x/2)

u[0, :] = initial_profile(x)

1. 现在我们可以简单地循环每一步，通过将A和前一行相乘来计算矩阵u的下一行：

for i in range(steps):
    u[i+1, :] = A @ u[i, :]

1. 最后，为了可视化我们刚刚计算的解，我们可以使用 Matplotlib 将解作为曲面绘制出来：

X, T = np.meshgrid(x, t)
fig = plt.figure()
ax = fig.add_subplot(projection="3d")

ax.plot_surface(T, X, u, cmap="hot")
ax.set_title("Solution of the heat equation")
ax.set_xlabel("t")
ax.set_ylabel("x")
ax.set_zlabel("u")

这导致了图 3.5中显示的曲面图：

图 3.5：使用有限差分方法计算的热方程解在范围 0 ≤ x ≤ 2 上的曲面图，使用了 10 个网格点

它是如何工作的…

有限差分方法通过用仅涉及函数值的简单分数替换每个导数来工作，我们可以估计这些分数。要实现这种方法，我们首先将空间范围和时间范围分解为若干离散间隔，由网格点分隔。这个过程称为离散化。然后我们使用微分方程和初始条件以及边界条件来形成连续的近似，这与solve_ivp例程在Solving differential equations numerically示例中使用的时间步进方法非常相似。

为了解决热方程这样的偏微分方程，我们至少需要三个信息。通常，对于热方程，这将以空间维度的边界条件的形式出现，告诉我们在杆的两端行为如何，以及时间维度的初始条件，即杆上的初始温度分布。

前面描述的有限差分方案通常被称为前向时间中心空间（FTCS）方案，因为我们使用前向有限差分来估计时间导数，使用中心有限差分来估计（二阶）空间导数。这些有限差分的公式如下：

和

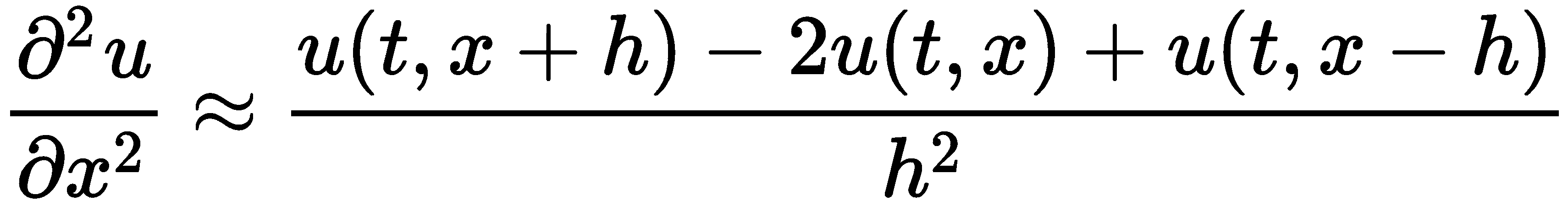
将这些近似代入热方程，并使用近似值u[i]^(j)来表示在i空间点上经过j时间步后u(t[j], x[i])的值，我们得到

可以重新排列以获得公式

粗略地说，这个方程表示给定点的下一个温度取决于以前时间的周围温度。这也显示了为什么r值的条件是必要的；如果条件不成立，右侧的中间项将是负的。

我们可以将这个方程组写成矩阵形式，

其中u*^{j*是包含近似*u[i]}j和矩阵A的向量，矩阵A在步骤 4中定义。这个矩阵是三对角的，这意味着非零条目出现在或邻近主对角线上。我们使用 SciPy sparse模块中的diag例程，这是一种定义这种矩阵的实用程序。这与本章中解方程配方中描述的过程非常相似。这个矩阵的第一行和最后一行都是零，除了在左上角和右下角，分别代表（不变的）边界条件。其他行的系数由微分方程两侧的有限差分近似给出。我们首先创建对角线条目和对角线上下方的条目，然后我们使用diags例程创建稀疏矩阵。矩阵应该有N+1*行和列，以匹配网格点的数量，并且我们将数据类型设置为双精度浮点数和 CSR 格式。

初始配置给我们向量u⁰，从这一点开始，我们可以通过简单地执行矩阵乘法来计算每个后续时间步骤，就像我们在步骤 7中看到的那样。

还有更多…

我们在这里描述的方法相当粗糙，因为近似可能变得不稳定，正如我们提到的，如果时间步长和空间步长的相对大小没有得到仔细控制。这种方法是显式的，因为每个时间步骤都是显式地使用来自上一个时间步骤的信息来计算的。还有隐式方法，它给出了一个可以求解以获得下一个时间步骤的方程组。不同的方案在解的稳定性方面具有不同的特性。

当函数f(t, x)不为 0 时，我们可以通过使用赋值来轻松适应这种变化

其中函数被适当地向量化以使这个公式有效。在解决问题的代码方面，我们只需要包括函数的定义，然后将解决方案的循环更改如下：

for i in range(steps):
    u[i+1, :] = A @ u[i, :] + f(t[i], x)

从物理上讲，这个函数代表了杆上每个点的外部热源（或者热池）。这可能随时间变化，这就是为什么一般来说，这个函数应该有t和x作为参数（尽管它们不一定都被使用）。

我们在这个例子中给出的边界条件代表了杆的两端保持在恒定温度为 0。这种边界条件有时被称为Dirichlet边界条件。还有Neumann边界条件，其中函数u的导数在边界处给定。例如，我们可能已经给出了边界条件

这在物理上可以被解释为杆的两端被绝缘，因此热量不能通过端点逃逸。对于这种边界条件，我们需要稍微修改矩阵A，但方法本质上保持不变。实际上，在边界的左侧插入一个虚拟的x值，并在左边界（x = 0）使用向后有限差分，我们得到

使用这个二阶有限差分近似，我们得到

这意味着我们矩阵的第一行应包含1-r，然后是r，然后是 0。对右手极限进行类似的计算得到矩阵的最后一行。

diag = [1-r, *(1-2*r for _ in range(N-1)), 1-r]
abv_diag = [*(r for _ in range(N))]
blw_diag = [*(r for _ in range(N))]

A = sparse.diags([blw_diag, diag, abv_diag], (-1, 0, 1), shape=(N+1, N+1), dtype=np.float64, format="csr")

对于涉及偏微分方程的更复杂问题，可能更适合使用有限元求解器。有限元方法使用比我们在本篇中看到的有限差分方法更复杂的方法来计算解决方案，通常比偏微分方程更灵活。然而，这需要更多依赖更高级数学理论的设置。另一方面，有一个用于使用有限元方法解决偏微分方程的 Python 包，如 FEniCS (fenicsproject.org)。使用 FEniCS 等包的优势在于它们通常针对性能进行了调整，这在解决复杂问题时对高精度至关重要。

另请参阅

FEniCS 文档介绍了有限元方法以及使用该包解决各种经典偏微分方程的示例。有关该方法和理论的更全面介绍可在以下书籍中找到：

• Johnson, C. (2009).Numerical solution of partial differential equations by the finite element method. Mineola, N.Y.: Dover Publications.

有关如何使用 Matplotlib 生成三维曲面图的更多详细信息，请参阅第二章中的曲面和等高线图食谱。

使用离散傅立叶变换进行信号处理

来自微积分中最有用的工具之一是傅立叶变换。粗略地说，傅立叶变换以可逆的方式改变了某些函数的表示。这种表示的改变在处理作为时间函数的信号时特别有用。在这种情况下，傅立叶变换将信号表示为频率函数；我们可以将其描述为从信号空间到频率空间的转换。这可以用于识别信号中存在的频率以进行识别和其他处理。在实践中，我们通常会有信号的离散样本，因此我们必须使用离散傅立叶变换来执行这种分析。幸运的是，有一种计算效率高的算法，称为快速傅立叶变换（FFT），用于对样本应用离散傅立叶变换。

*我们将遵循使用 FFT 处理嘈杂信号的常见过程。第一步是应用 FFT 并使用数据计算信号的功率谱密度。然后我们识别峰值并滤除对信号贡献不足够大的频率。然后我们应用逆 FFT 来获得滤波后的信号。

在本篇中，我们使用 FFT 来分析信号的样本，并识别存在的频率并清除信号中的噪音。

准备工作

对于本篇，我们只需要导入 NumPy 和 Matplotlib 包，如往常一样命名为np和plt。

如何做…

按照以下说明使用 FFT 处理嘈杂信号：

1. 我们定义一个函数来生成我们的基础信号：

def signal(t, freq_1=4.0, freq_2=7.0):
    return np.sin(freq_1 * 2 * np.pi * t) + np.sin(freq_2 * 2 *
        np.pi * t)

1. 接下来，我们通过向基础信号添加一些高斯噪声来创建我们的样本信号。我们还创建一个数组，以便在以后方便时保存样本t值处的真实信号：

state = np.random.RandomState(12345)
sample_size = 2**7 # 128
sample_t = np.linspace(0, 4, sample_size)
sample_y = signal(sample_t) + state.standard_normal(sample_size)
sample_d = 4./(sample_size - 1) # Spacing for linspace array
true_signal = signal(sample_t)

1. 我们使用 NumPy 的fft模块来计算离散傅立叶变换。在开始分析之前，我们从 NumPy 中导入这个模块：

from numpy import fft

1. 要查看嘈杂信号的样子，我们可以绘制样本信号点并叠加真实信号：

fig1, ax1 = plt.subplots()
ax1.plot(sample_t, sample_y, "k.", label="Noisy signal")
ax1.plot(sample_t, signal(sample_t), "k--", label="True signal")

ax1.set_title("Sample signal with noise")
ax1.set_xlabel("Time")
ax1.set_ylabel("Amplitude")
ax1.legend()

此处创建的图表显示在图 3.6中。正如我们所看到的，嘈杂信号与真实信号几乎没有相似之处（用虚线表示）：

图 3.6：带真实信号的噪声信号样本

1. 现在，我们将使用离散傅立叶变换来提取样本信号中存在的频率。fft模块中的fft例程执行 FFT（离散傅立叶变换）：

spectrum = fft.fft(sample_y)

1. fft模块提供了一个用于构建适当频率值的例程，称为fftfreq。为了方便起见，我们还生成一个包含正频率出现的整数的数组：

freq = fft.fftfreq(sample_size, sample_d)
pos_freq_i = np.arange(1, sample_size//2, dtype=int)

1. 接下来，计算信号的功率谱密度（PSD）如下：

psd = np.abs(spectrum[pos_freq_i])**2 + np.abs(spectrum[-
        pos_freq_i])**2

1. 现在，我们可以绘制信号的正频率的 PSD，并使用这个图来识别频率：

fig2, ax2 = plt.subplots()
ax2.plot(freq[pos_freq_i], psd)
ax2.set_title("PSD of the noisy signal")
ax2.set_xlabel("Frequency")
ax2.set_ylabel("Density")

结果可以在图 3.7中看到。我们可以在这个图表中看到大约在 4 和 7 左右有尖峰，这些是我们之前定义的信号的频率：

图 3.7：使用 FFT 生成的信号的功率谱密度

1. 我们可以识别这两个频率，尝试从噪声样本中重建真实信号。所有出现的次要峰值都不大于 10,000，所以我们可以将其作为滤波器的截止值。现在，我们从所有正频率索引的列表中提取（希望是 2 个）对应于 PSD 中大于 10,000 的峰值的索引：

filtered = pos_freq_i[psd > 1e4]

1. 接下来，我们创建一个新的干净频谱，其中只包含我们从噪声信号中提取的频率。我们通过创建一个只包含 0 的数组，然后将spectrum的值从对应于滤波频率及其负值的索引复制过来来实现这一点：

new_spec = np.zeros_like(spectrum)
new_spec[filtered] = spectrum[filtered]
new_spec[-filtered] = spectrum[-filtered]

1. 现在，我们使用逆 FFT（使用ifft例程）将这个干净的频谱转换回原始样本的时间域。我们使用 NumPy 的real例程取实部以消除错误的虚部：

new_sample = np.real(fft.ifft(new_spec))

1. 最后，我们绘制这个滤波信号和真实信号进行比较：

fig3, ax3 = plt.subplots()
ax3.plot(sample_t, true_signal, color="#8c8c8c", linewidth=1.5, label="True signal")
ax3.plot(sample_t, new_sample, "k--", label="Filtered signal")
ax3.legend()
ax3.set_title("Plot comparing filtered signal and true signal")
ax3.set_xlabel("Time")
ax3.set_ylabel("Amplitude")

步骤 12的结果显示在图 3.8中。我们可以看到，滤波信号与真实信号非常接近，除了一些小的差异：

图 3.8：比较使用 FFT 和滤波生成的滤波信号与真实信号的图

工作原理…

函数f(t)的傅立叶变换由积分给出

离散傅立叶变换如下：

这里，f[k]值是复数形式的样本值。可以使用前面的公式计算离散傅立叶变换，但实际上这并不高效。使用这个公式计算的复杂度是O(N²)。FFT 算法将复杂度提高到O(N log N)，这显然更好。书籍Numerical Recipes（在进一步阅读部分给出完整的参考文献细节）对 FFT 算法和离散傅立叶变换有很好的描述。

我们将对从已知信号（具有已知频率模式）生成的样本应用离散傅立叶变换，以便我们可以看到我们获得的结果与原始信号之间的联系。为了保持这个信号简单，我们创建了一个只有两个频率分量（值为 4 和 7）的信号。从这个信号，我们生成了我们分析的样本。由于 FFT 的工作方式，最好是样本的大小是 2 的幂；如果不是这种情况，我们可以用零元素填充样本使其成为这种情况。我们向样本信号添加了一些高斯噪声，这是一个正态分布的随机数。

fft例程返回的数组包含N+1个元素，其中N是样本大小。索引为 0 的元素对应于 0 频率，或者直流偏移。接下来的N/2个元素是对应于正频率的值，最后的N/2个元素是对应于负频率的值。频率的实际值由采样点数N和采样间距确定，在这个例子中，采样间距存储在sample_d中。

频率ω处的功率谱密度由以下公式给出

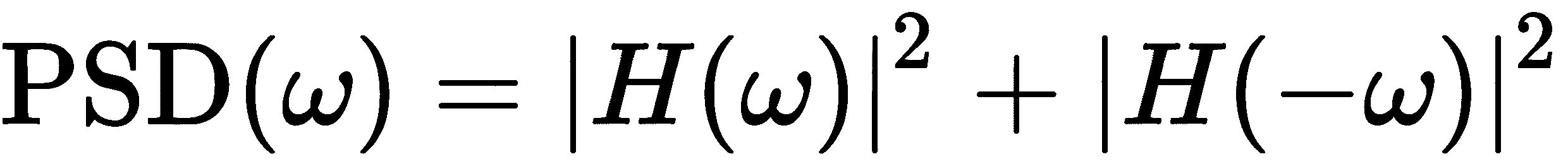
其中H(ω)代表信号在频率ω处的傅里叶变换。功率谱密度测量了每个频率对整体信号的贡献，这就是为什么我们在大约 4 和 7 处看到峰值。由于 Python 索引允许我们对从序列末尾开始的元素使用负索引，我们可以使用正索引数组从spectrum中获取正频率和负频率元素。

在步骤 9中，我们提取了在图表上峰值超过 10,000 的两个频率的索引。对应于这些索引的频率分别是 3.984375 和 6.97265625，它们并不完全等于 4 和 7，但非常接近。这种差异的原因是我们使用有限数量的点对连续信号进行了采样。（使用更多点当然会得到更好的近似。）

在步骤 11中，我们提取了从逆 FFT 返回的数据的实部。这是因为从技术上讲，FFT 处理复杂数据。由于我们的数据只包含实数据，我们期望这个新信号也只包含实数据。然而，会有一些小错误产生，这意味着结果并非完全是实数。我们可以通过取逆 FFT 的实部来纠正这一点。这是合适的，因为我们可以看到虚部非常小。

我们可以在图 3.8中看到，滤波信号非常接近真实信号，但并非完全相同。这是因为，如前所述，我们正在用相对较小的样本来逼近连续信号。

还有更多…

在生产环境中的信号处理可能会使用专门的软件包，比如scipy中的signal模块，或者一些更低级的代码或硬件来执行信号的滤波或清理。这个示例更多地应该被看作是 FFT 作为处理从某种基础周期结构（信号）采样的数据的工具的演示。FFT 对于解决偏微分方程非常有用，比如在数值解偏微分方程食谱中看到的热方程。

另请参阅

有关随机数和正态分布（高斯）的更多信息可以在第四章中找到，处理随机性和概率。

进一步阅读

微积分是每门本科数学课程中非常重要的一部分。有许多关于微积分的优秀教科书，包括 Spivak 的经典教科书和 Adams 和 Essex 的更全面的课程：

• Spivak, M. (2006). Calculus. 3rd ed. Cambridge: Cambridge University Press

• Adams, R. and Essex, C. (2018). Calculus: A Complete Course. 9th ed. Don Mills, Ont: Pearson.Guassian

关于数值微分和积分的良好来源是经典的数值方法书，其中详细描述了如何在 C++中解决许多计算问题的理论概述：

• Press, W., Teukolsky, S., Vetterling, W. and Flannery, B. (2007). Numerical recipes: The Art of Scientific Computing. 3rd ed. Cambridge: Cambridge University Press****