JAX 中的广义卷积
[外链图片转存中…(img-VNybejd1-1718950765073)] 
JAX 提供了多种接口来跨数据计算卷积,包括:
-
jax.numpy.convolve()(也有jax.numpy.correlate()) -
jax.scipy.signal.convolve()(也有correlate()) -
jax.scipy.signal.convolve2d()(也有correlate2d()) -
jax.lax.conv_general_dilated()
对于基本的卷积操作,jax.numpy 和 jax.scipy 的操作通常足够使用。如果要进行更一般的批量多维卷积,jax.lax 函数是你应该开始的地方。
基本的一维卷积
基本的一维卷积由jax.numpy.convolve()实现,它为numpy.convolve()提供了一个 JAX 接口。这里是通过卷积实现的简单一维平滑的例子:
import matplotlib.pyplot as plt
from jax import random
import jax.numpy as jnp
import numpy as np
key = random.key(1701)
x = jnp.linspace(0, 10, 500)
y = jnp.sin(x) + 0.2 * random.normal(key, shape=(500,))
window = jnp.ones(10) / 10
y_smooth = jnp.convolve(y, window, mode='same')
plt.plot(x, y, 'lightgray')
plt.plot(x, y_smooth, 'black');

mode参数控制如何处理边界条件;这里我们使用mode='same'确保输出与输入大小相同。
欲了解更多信息,请参阅jax.numpy.convolve()文档,或与原始numpy.convolve()函数相关的文档。
基本的N维卷积
对于N维卷积,jax.scipy.signal.convolve()提供了类似于jax.numpy.convolve()的界面,推广到N维。
例如,这里是一种使用高斯滤波器进行图像去噪的简单方法:
from scipy import misc
import jax.scipy as jsp
fig, ax = plt.subplots(1, 3, figsize=(12, 5))
# Load a sample image; compute mean() to convert from RGB to grayscale.
image = jnp.array(misc.face().mean(-1))
ax[0].imshow(image, cmap='binary_r')
ax[0].set_title('original')
# Create a noisy version by adding random Gaussian noise
key = random.key(1701)
noisy_image = image + 50 * random.normal(key, image.shape)
ax[1].imshow(noisy_image, cmap='binary_r')
ax[1].set_title('noisy')
# Smooth the noisy image with a 2D Gaussian smoothing kernel.
x = jnp.linspace(-3, 3, 7)
window = jsp.stats.norm.pdf(x) * jsp.stats.norm.pdf(x[:, None])
smooth_image = jsp.signal.convolve(noisy_image, window, mode='same')
ax[2].imshow(smooth_image, cmap='binary_r')
ax[2].set_title('smoothed');
/tmp/ipykernel_1464/4118182506.py:7: DeprecationWarning: scipy.misc.face has been deprecated in SciPy v1.10.0; and will be completely removed in SciPy v1.12.0\. Dataset methods have moved into the scipy.datasets module. Use scipy.datasets.face instead.
image = jnp.array(misc.face().mean(-1))
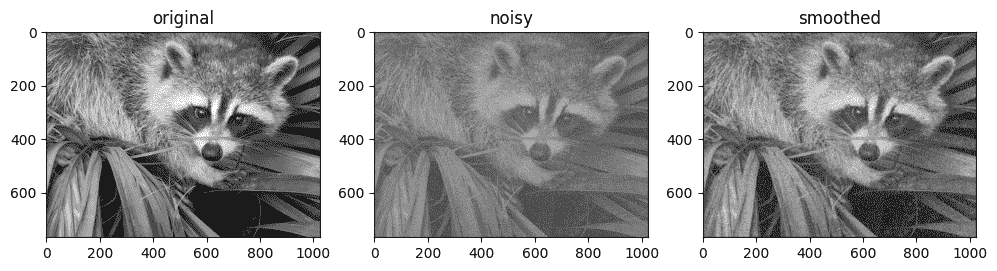
如同一维情况,我们使用mode='same'指定如何处理边缘。有关N维卷积中可用选项的更多信息,请参阅jax.scipy.signal.convolve()文档。
广义卷积
对于在构建深度神经网络中通常有用的更一般类型的批量卷积,JAX 和 XLA 提供了非常通用的 N 维conv_general_dilated函数,但如何使用它并不是很明显。我们将给出一些常见用例的示例。
一篇关于卷积算术的家族调查,卷积算术指南,强烈推荐阅读!
让我们定义一个简单的对角边缘核:
# 2D kernel - HWIO layout
kernel = jnp.zeros((3, 3, 3, 3), dtype=jnp.float32)
kernel += jnp.array([[1, 1, 0],
[1, 0,-1],
[0,-1,-1]])[:, :, jnp.newaxis, jnp.newaxis]
print("Edge Conv kernel:")
plt.imshow(kernel[:, :, 0, 0]);
Edge Conv kernel:

接下来我们将创建一个简单的合成图像:
# NHWC layout
img = jnp.zeros((1, 200, 198, 3), dtype=jnp.float32)
for k in range(3):
x = 30 + 60*k
y = 20 + 60*k
img = img.at[0, x:x+10, y:y+10, k].set(1.0)
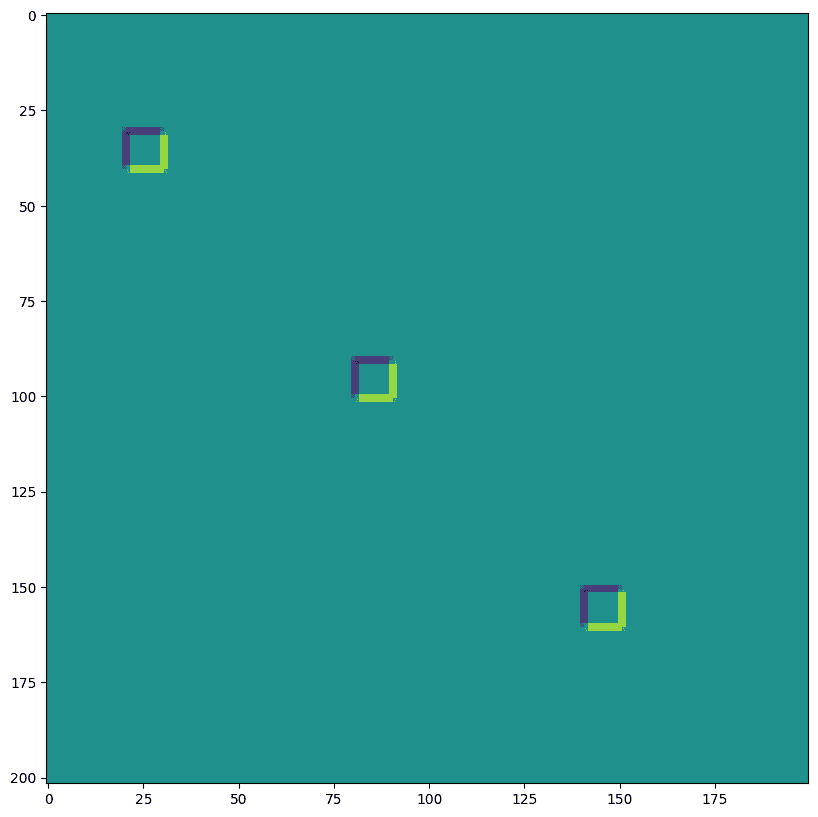
print("Original Image:")
plt.imshow(img[0]);
Original Image:

lax.conv 和 lax.conv_with_general_padding
这些是卷积的简单便捷函数
️⚠️ 便捷函数 lax.conv,lax.conv_with_general_padding 假定 NCHW 图像和 OIHW 卷积核。
from jax import lax
out = lax.conv(jnp.transpose(img,[0,3,1,2]), # lhs = NCHW image tensor
jnp.transpose(kernel,[3,2,0,1]), # rhs = OIHW conv kernel tensor
(1, 1), # window strides
'SAME') # padding mode
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(np.array(out)[0,0,:,:]);
out shape: (1, 3, 200, 198)
First output channel:

out = lax.conv_with_general_padding(
jnp.transpose(img,[0,3,1,2]), # lhs = NCHW image tensor
jnp.transpose(kernel,[2,3,0,1]), # rhs = IOHW conv kernel tensor
(1, 1), # window strides
((2,2),(2,2)), # general padding 2x2
(1,1), # lhs/image dilation
(1,1)) # rhs/kernel dilation
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(np.array(out)[0,0,:,:]);
out shape: (1, 3, 202, 200)
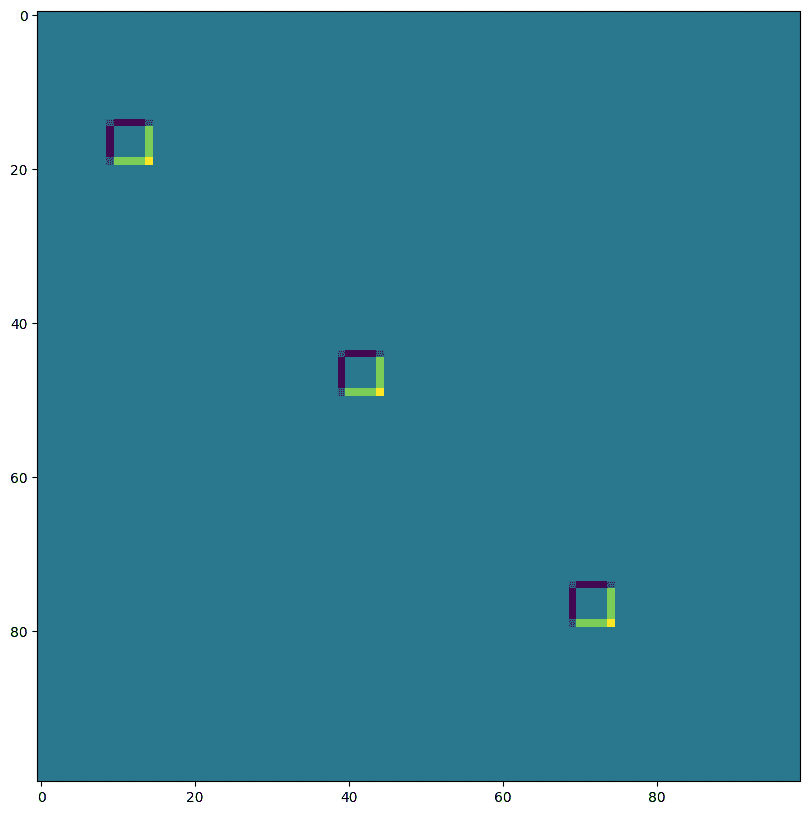
First output channel:
维度编号定义了 conv_general_dilated 的维度布局
重要的参数是轴布局的三元组:(输入布局,卷积核布局,输出布局)
-
N - 批次维度
-
H - 空间高度
-
W - 空间宽度
-
C - 通道维度
-
I - 卷积核 输入 通道维度
-
O - 卷积核 输出 通道维度
⚠️ 为了展示维度编号的灵活性,我们选择了 NHWC 图像和 HWIO 卷积核约定,如下所示 lax.conv_general_dilated。
dn = lax.conv_dimension_numbers(img.shape, # only ndim matters, not shape
kernel.shape, # only ndim matters, not shape
('NHWC', 'HWIO', 'NHWC')) # the important bit
print(dn)
ConvDimensionNumbers(lhs_spec=(0, 3, 1, 2), rhs_spec=(3, 2, 0, 1), out_spec=(0, 3, 1, 2))
SAME 填充,无步长,无扩张
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'SAME', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 200, 198, 3)
First output channel:

VALID 填充,无步长,无扩张
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'VALID', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "DIFFERENT from above!")
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 198, 196, 3) DIFFERENT from above!
First output channel:

SAME 填充,2,2 步长,无扩张
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(2,2), # window strides
'SAME', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, " <-- half the size of above")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 100, 99, 3) <-- half the size of above
First output channel:
VALID 填充,无步长,rhs 卷积核扩张 ~ 膨胀卷积(用于演示)
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'VALID', # padding mode
(1,1), # lhs/image dilation
(12,12), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 176, 174, 3)
First output channel:

VALID 填充,无步长,lhs=input 扩张 ~ 转置卷积
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
((0, 0), (0, 0)), # padding mode
(2,2), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "<-- larger than original!")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 397, 393, 3) <-- larger than original!
First output channel:

我们可以用最后一个示例,比如实现 转置卷积:
# The following is equivalent to tensorflow:
# N,H,W,C = img.shape
# out = tf.nn.conv2d_transpose(img, kernel, (N,2*H,2*W,C), (1,2,2,1))
# transposed conv = 180deg kernel rotation plus LHS dilation
# rotate kernel 180deg:
kernel_rot = jnp.rot90(jnp.rot90(kernel, axes=(0,1)), axes=(0,1))
# need a custom output padding:
padding = ((2, 1), (2, 1))
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel_rot, # rhs = conv kernel tensor
(1,1), # window strides
padding, # padding mode
(2,2), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "<-- transposed_conv")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(np.array(out)[0,:,:,0]);
out shape: (1, 400, 396, 3) <-- transposed_conv
First output channel:

1D 卷积
你不仅限于 2D 卷积,下面是一个简单的 1D 演示:
# 1D kernel - WIO layout
kernel = jnp.array([[[1, 0, -1], [-1, 0, 1]],
[[1, 1, 1], [-1, -1, -1]]],
dtype=jnp.float32).transpose([2,1,0])
# 1D data - NWC layout
data = np.zeros((1, 200, 2), dtype=jnp.float32)
for i in range(2):
for k in range(2):
x = 35*i + 30 + 60*k
data[0, x:x+30, k] = 1.0
print("in shapes:", data.shape, kernel.shape)
plt.figure(figsize=(10,5))
plt.plot(data[0]);
dn = lax.conv_dimension_numbers(data.shape, kernel.shape,
('NWC', 'WIO', 'NWC'))
print(dn)
out = lax.conv_general_dilated(data, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,), # window strides
'SAME', # padding mode
(1,), # lhs/image dilation
(1,), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
plt.figure(figsize=(10,5))
plt.plot(out[0]);
in shapes: (1, 200, 2) (3, 2, 2)
ConvDimensionNumbers(lhs_spec=(0, 2, 1), rhs_spec=(2, 1, 0), out_spec=(0, 2, 1))
out shape: (1, 200, 2)


3D 卷积
import matplotlib as mpl
# Random 3D kernel - HWDIO layout
kernel = jnp.array([
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, -1, 0], [-1, 0, -1], [0, -1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]]],
dtype=jnp.float32)[:, :, :, jnp.newaxis, jnp.newaxis]
# 3D data - NHWDC layout
data = jnp.zeros((1, 30, 30, 30, 1), dtype=jnp.float32)
x, y, z = np.mgrid[0:1:30j, 0:1:30j, 0:1:30j]
data += (jnp.sin(2*x*jnp.pi)*jnp.cos(2*y*jnp.pi)*jnp.cos(2*z*jnp.pi))[None,:,:,:,None]
print("in shapes:", data.shape, kernel.shape)
dn = lax.conv_dimension_numbers(data.shape, kernel.shape,
('NHWDC', 'HWDIO', 'NHWDC'))
print(dn)
out = lax.conv_general_dilated(data, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1,1), # window strides
'SAME', # padding mode
(1,1,1), # lhs/image dilation
(1,1,1), # rhs/kernel dilation
dn) # dimension_numbers
print("out shape: ", out.shape)
# Make some simple 3d density plots:
from mpl_toolkits.mplot3d import Axes3D
def make_alpha(cmap):
my_cmap = cmap(jnp.arange(cmap.N))
my_cmap[:,-1] = jnp.linspace(0, 1, cmap.N)**3
return mpl.colors.ListedColormap(my_cmap)
my_cmap = make_alpha(plt.cm.viridis)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(x.ravel(), y.ravel(), z.ravel(), c=data.ravel(), cmap=my_cmap)
ax.axis('off')
ax.set_title('input')
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(x.ravel(), y.ravel(), z.ravel(), c=out.ravel(), cmap=my_cmap)
ax.axis('off')
ax.set_title('3D conv output');
in shapes: (1, 30, 30, 30, 1) (3, 3, 3, 1, 1)
ConvDimensionNumbers(lhs_spec=(0, 4, 1, 2, 3), rhs_spec=(4, 3, 0, 1, 2), out_spec=(0, 4, 1, 2, 3))
out shape: (1, 30, 30, 30, 1)


开发者文档
JAX 欢迎来自社区的贡献。请查看以下各种安装指南,以作为开发人员设置,并且开发人员专注的资源,如 Jax Enhancement Proposals。
-
参与 JAX 开发
-
从源代码构建
-
内部 API
-
Autodidax: 从零开始构建 JAX 核心
-
JAX Enhancement Proposals (JEPs)
-
调查回归
贡献给 JAX
每个人都可以贡献到 JAX,并且我们重视每个人的贡献。有几种贡献方式,包括:
JAX 项目遵循Google 的开源社区准则。
贡献的方式
我们欢迎拉取请求,特别是对于那些标记有欢迎贡献或好的首次问题的问题。
对于其他建议,我们要求您首先在 GitHub 的问题或讨论中寻求对您计划贡献的反馈。
使用拉取请求贡献代码
我们所有的开发都是使用 git 进行的,所以假定您具备基本知识。
按照以下步骤贡献代码:
-
签署Google 贡献者许可协议 (CLA)。有关更多信息,请参阅下面的拉取请求检查清单。
-
在存储库页面上点击Fork按钮来分叉 JAX 存储库。这将在您自己的账户中创建 JAX 存储库的副本。
-
在本地安装 Python >= 3.9 以便运行测试。
-
使用
pip从源码安装您的分支。这允许您修改代码并立即测试:git clone https://github.com/YOUR_USERNAME/jax cd jax pip install -r build/test-requirements.txt # Installs all testing requirements. pip install -e ".[cpu]" # Installs JAX from the current directory in editable mode. -
将 JAX 存储库添加为上游远程,以便您可以使用它来同步您的更改。
git remote add upstream https://www.github.com/google/jax -
创建一个分支,在该分支上进行开发:
git checkout -b name-of-change并使用您喜欢的编辑器实现您的更改(我们推荐Visual Studio Code)。
-
通过从存储库顶部运行以下命令来确保您的代码通过 JAX 的 lint 和类型检查:
pip install pre-commit pre-commit run --all有关更多详细信息,请参阅代码规范和类型检查。
-
确保通过从存储库顶部运行以下命令来通过测试:
pytest -n auto tests/JAX 的测试套件非常庞大,因此如果您知道涵盖您更改的特定测试文件,您可以限制测试为该文件;例如:
pytest -n auto tests/lax_scipy_test.py您可以使用
pytest -k标志进一步缩小测试范围以匹配特定的测试名称:pytest -n auto tests/lax_scipy_test.py -k testLogSumExpJAX 还提供了对运行哪些特定测试有更精细控制的方式;有关更多信息,请参阅运行测试。
-
一旦您对自己的更改感到满意,请按如下方式创建提交(如何编写提交消息):
git add file1.py file2.py ... git commit -m "Your commit message"然后将您的代码与主存储库同步:
git fetch upstream git rebase upstream/main最后,将您的提交推送到开发分支,并在您的分支中创建一个远程分支,以便从中创建拉取请求:
git push --set-upstream origin name-of-change请确保您的贡献是一个单一提交(参见单一更改提交和拉取请求)
-
从 JAX 仓库创建一个拉取请求并发送进行审查。在准备您的 PR 时,请检查 JAX 拉取请求检查列表,并在需要更多关于使用拉取请求的信息时参考 GitHub 帮助。
JAX 拉取请求检查列表
当您准备一个 JAX 拉取请求时,请牢记以下几点:
Google 贡献者许可协议
参与此项目必须附有 Google 贡献者许可协议(CLA)。您(或您的雇主)保留对您贡献的版权;这只是让我们可以在项目的一部分中使用和重新分发您的贡献的许可。请访问 cla.developers.google.com/ 查看您当前已有的协议或签署新协议。
通常您只需要提交一次 CLA,所以如果您已经提交过一个(即使是为不同的项目),您可能不需要再次提交。如果您不确定是否已签署了 CLA,您可以打开您的 PR,我们友好的 CI 机器人将为您检查。
单一更改提交和拉取请求
一个 git 提交应该是一个独立的、单一的更改,并带有描述性的消息。这有助于审查和在后期发现问题时识别或还原更改。
拉取请求通常由单一 git 提交组成。(在某些情况下,例如进行大型重构或内部重写时,可能会包含多个提交。)在准备进行审查的拉取请求时,如果可能的话,请提前将多个提交合并。可能会使用 git rebase -i 命令来实现这一点。### 代码风格检查和类型检查
JAX 使用 mypy 和 ruff 来静态测试代码质量;在本地运行这些检查的最简单方法是通过 pre-commit 框架:
pip install pre-commit
pre-commit run --all
如果您的拉取请求涉及文档笔记本,请注意还将对其运行一些检查(有关更多详细信息,请参阅更新笔记本)。
完整的 GitHub 测试套件
您的 PR 将自动通过 GitHub CI 运行完整的测试套件,该套件涵盖了多个 Python 版本、依赖版本和配置选项。这些测试通常会发现您在本地没有捕捉到的失败;为了修复问题,您可以将新的提交推送到您的分支。
受限测试套件
一旦您的 PR 被审查通过,JAX 的维护者将其标记为 Pull Ready。这将触发一系列更广泛的测试,包括在标准 GitHub CI 中不可用的 GPU 和 TPU 后端的测试。这些测试的详细结果不对公众可见,但负责审查您的 PR 的 JAX 维护者将与您沟通任何可能揭示的失败;例如,TPU 上的数值测试通常需要与 CPU 不同的容差。
从源代码构建
首先,获取 JAX 源代码:
git clone https://github.com/google/jax
cd jax
构建 JAX 涉及两个步骤:
-
构建或安装用于
jax的 C++支持库jaxlib。 -
安装
jaxPython 包。
构建或安装jaxlib
使用 pip 安装jaxlib
如果您只修改了 JAX 的 Python 部分,我们建议使用 pip 从预构建的 wheel 安装jaxlib:
pip install jaxlib
请参阅JAX 自述文件获取有关 pip 安装的完整指南(例如,用于 GPU 和 TPU 支持)。
从源代码构建jaxlib
要从源代码构建jaxlib,还必须安装一些先决条件:
-
C++编译器(g++、clang 或 MSVC)
在 Ubuntu 或 Debian 上,可以使用以下命令安装所需的先决条件:
sudo apt install g++ python python3-dev如果你在 Mac 上进行构建,请确保安装了 XCode 和 XCode 命令行工具。
请参阅下面的 Windows 构建说明。
-
无需在本地安装 Python 依赖项,因为在构建过程中将忽略你的系统 Python;请查看有关管理封闭 Python 的详细信息。
要为 CPU 或 TPU 构建jaxlib,可以运行:
python build/build.py
pip install dist/*.whl # installs jaxlib (includes XLA)
要为与当前系统安装的 Python 版本不同的版本构建 wheel,请将--python_version标志传递给构建命令:
python build/build.py --python_version=3.12
本文的其余部分假定你正在为与当前系统安装匹配的 Python 版本构建。如果需要为不同版本构建,只需每次调用python build/build.py时附加--python_version=<py version>标志。请注意,无论是否传递--python_version参数,Bazel 构建始终将使用封闭的 Python 安装。
有两种方法可以使用 CUDA 支持构建jaxlib:(1) 使用python build/build.py --enable_cuda生成带有 cuda 支持的 jaxlib wheel,或者 (2) 使用python build/build.py --enable_cuda --build_gpu_plugin --gpu_plugin_cuda_version=12生成三个 wheel(不带 cuda 的 jaxlib,jax-cuda-plugin 和 jax-cuda-pjrt)。你可以将gpu_plugin_cuda_version设置为 11 或 12。
查看python build/build.py --help以获取配置选项,包括指定 CUDA 和 CUDNN 路径的方法,这些必须已安装。这里的python应该是你的 Python 3 解释器的名称;在某些系统上,你可能需要使用python3。尽管使用python调用脚本,但 Bazel 将始终使用其自己的封闭 Python 解释器和依赖项,只有build/build.py脚本本身将由你的系统 Python 解释器处理。默认情况下,wheel 将写入当前目录的dist/子目录。
使用修改后的 XLA 存储库从源代码构建 jaxlib。
JAX 依赖于 XLA,其源代码位于XLA GitHub 存储库中。默认情况下,JAX 使用 XLA 存储库的固定副本,但在开发 JAX 时,我们经常希望使用本地修改的 XLA 副本。有两种方法可以做到这一点:
-
使用 Bazel 的
override_repository功能,您可以将其作为命令行标志传递给build.py,如下所示:python build/build.py --bazel_options=--override_repository=xla=/path/to/xla -
修改 JAX 源代码根目录中的
WORKSPACE文件,以指向不同的 XLA 树。
要向 XLA 贡献更改,请向 XLA 代码库发送 PR。
JAX 固定的 XLA 版本定期更新,但在每次 jaxlib 发布之前会进行特定更新。
在 Windows 上从源代码构建 jaxlib 的附加说明
在 Windows 上,按照 安装 Visual Studio 的指南来设置 C++ 工具链。需要使用 Visual Studio 2019 版本 16.5 或更新版本。如果需要启用 CUDA 进行构建,请按照 CUDA 安装指南 设置 CUDA 环境。
JAX 构建使用符号链接,需要您激活 开发者模式。
您可以使用其 Windows 安装程序 安装 Python,或者如果您更喜欢,可以使用 Anaconda 或 Miniconda 设置 Python 环境。
Bazel 的某些目标使用 bash 实用程序进行脚本编写,因此需要 MSYS2。有关详细信息,请参阅 在 Windows 上安装 Bazel。安装以下软件包:
pacman -S patch coreutils
安装 coreutils 后,realpath 命令应存在于您的 shell 路径中。
安装完成后。打开 PowerShell,并确保 MSYS2 在当前会话的路径中。确保 bazel、patch 和 realpath 可访问。激活 conda 环境。以下命令启用 CUDA 并进行构建,请根据您的需求进行调整:
python .\build\build.py `
--enable_cuda `
--cuda_path='C:/Program Files/NVIDIA GPU Computing Toolkit/CUDA/v10.1' `
--cudnn_path='C:/Program Files/NVIDIA GPU Computing Toolkit/CUDA/v10.1' `
--cuda_version='10.1' `
--cudnn_version='7.6.5'
要添加调试信息进行构建,请加上标志 --bazel_options='--copt=/Z7'。
为 AMD GPU 构建 ROCM jaxlib 的附加说明
您需要安装多个 ROCM/HIP 库以在 ROCM 上进行构建。例如,在具有 AMD 的 apt 存储库 的 Ubuntu 机器上,需要安装多个软件包:
sudo apt install miopen-hip hipfft-dev rocrand-dev hipsparse-dev hipsolver-dev \
rccl-dev rccl hip-dev rocfft-dev roctracer-dev hipblas-dev rocm-device-libs
要使用 ROCM 支持构建 jaxlib,可以运行以下构建命令,并根据您的路径和 ROCM 版本进行适当调整。
python build/build.py --enable_rocm --rocm_path=/opt/rocm-5.7.0
AMD 的 XLA 代码库分支可能包含在上游 XLA 代码库中不存在的修复程序。如果遇到上游代码库的问题,可以尝试使用 AMD 的分支,方法是克隆他们的代码库:
git clone https://github.com/ROCmSoftwarePlatform/xla.git
并使用以下命令覆盖构建 JAX 所用的 XLA 代码库:
python build/build.py --enable_rocm --rocm_path=/opt/rocm-5.7.0 \
--bazel_options=--override_repository=xla=/path/to/xla-rocm
管理封闭 Python
为了确保 JAX 的构建可复制,并在支持的平台(Linux、Windows、MacOS)上表现一致,并且正确隔离于本地系统的特定细节,我们依赖于隔离的 Python(参见rules_python)来执行通过 Bazel 执行的所有构建和测试命令。这意味着在构建期间将忽略系统 Python 安装,并且 Python 解释器以及所有 Python 依赖项将由 bazel 直接管理。
指定 Python 版本
运行build/build.py工具时,将自动设置隔离的 Python 版本,以匹配您用于运行build/build.py脚本的 Python 版本。若要显式选择特定版本,可以向该工具传递--python_version参数:
python build/build.py --python_version=3.12
在幕后,隔离的 Python 版本由HERMETIC_PYTHON_VERSION环境变量控制,在运行build/build.py时将自动设置。如果直接运行 bazel,则可能需要以以下某种方式显式设置该变量:
# Either add an entry to your `.bazelrc` file
build --repo_env=HERMETIC_PYTHON_VERSION=3.12
# OR pass it directly to your specific build command
bazel build <target> --repo_env=HERMETIC_PYTHON_VERSION=3.12
# OR set the environment variable globally in your shell:
export HERMETIC_PYTHON_VERSION=3.12
您可以通过在运行之间简单切换--python_version的值来在同一台机器上连续运行不同版本的 Python 进行构建和测试。构建缓存中的所有与 Python 无关的部分将保留并在后续构建中重用。
指定 Python 依赖项
在 bazel 构建期间,所有 JAX 的 Python 依赖项都被固定到它们的特定版本。这是确保构建可复制性所必需的。JAX 依赖项的完整传递闭包以及其相应的哈希在build/requirements_lock_<python version>.txt文件中指定(例如,Python 3.12的build/requirements_lock_3_12.txt)。
要更新锁定文件,请确保build/requirements.in包含所需的直接依赖项列表,然后执行以下命令(此命令将在幕后调用pip-compile):
python build/build.py --requirements_update --python_version=3.12
或者,如果需要更多控制,可以直接运行 bazel 命令(这两个命令是等效的):
bazel run //build:requirements.update --repo_env=HERMETIC_PYTHON_VERSION=3.12
其中3.12是您希望更新的 Python 版本。
注意,由于仍然使用的是幕后的pip和pip-compile工具,因此大多数由这些工具支持的命令行参数和功能也将被 Bazel 要求更新命令所承认。例如,如果希望更新程序考虑预发布版本,只需将--pre参数传递给 bazel 命令:
bazel run //build:requirements.update --repo_env=HERMETIC_PYTHON_VERSION=3.12 -- --pre
指定本地构建的依赖项
如果需要依赖于本地的.whl文件,例如您新构建的 jaxlib wheel,可以在build/requirements.in中添加轮的路径,并重新运行所选 Python 版本的要求更新器命令。例如:
echo -e "\n$(realpath jaxlib-0.4.27.dev20240416-cp312-cp312-manylinux2014_x86_64.whl)" >> build/requirements.in
python build/build.py --requirements_update --python_version=3.12
指定夜间构建的依赖项
为了构建和测试最新的、潜在不稳定的 Python 依赖关系集合,我们提供了一个特殊版本的依赖关系更新命令,如下所示:
python build/build.py --requirements_nightly_update --python_version=3.12
或者,如果你直接运行bazel(这两个命令是等效的):
bazel run //build:requirements_nightly.update --repo_env=HERMETIC_PYTHON_VERSION=3.12
与常规更新程序的区别在于,默认情况下它会接受预发布、开发和夜间包,还将搜索 https://pypi.anaconda.org/scientific-python-nightly-wheels/simple 作为额外的索引 URL,并且不会在生成的要求锁文件中放置哈希值。
使用预发布版本的 Python 进行构建
我们支持所有当前版本的 Python,但如果你需要针对不同版本(例如尚未正式发布的最新不稳定版本)进行构建和测试,请按照以下说明操作。
- 确保你已安装构建 Python 解释器本身所需的必要 Linux 软件包,以及从源代码安装关键软件包(如
numpy或scipy)。在典型的 Debian 系统上,你可能需要安装以下软件包:
sudo apt-get update
sudo apt-get build-dep python3 -y
sudo apt-get install pkg-config zlib1g-dev libssl-dev -y
# to build scipy
sudo apt-get install libopenblas-dev -y
-
检查你的
WORKSPACE文件,并确保其中有指向你想要构建的 Python 版本的custom_python_interpreter()条目。 -
运行
bazel build @python_dev//:python_dev来构建 Python 解释器。默认情况下,它将使用 GCC 编译器进行构建。如果你希望使用 clang 进行构建,则需要设置相应的环境变量(例如--repo_env=CC=/usr/lib/llvm-17/bin/clang --repo_env=CXX=/usr/lib/llvm-17/bin/clang++)。 -
检查上一个命令的输出。在其末尾,你会找到一个
python_register_toolchains()入口的代码片段,其中包含你新构建的 Python。将该代码片段复制到你的WORKSPACE文件中,可以选择是在python_init_toolchains()入口后面(添加新版本的 Python),还是替换它(替换类似于 3.12 的现有版本,例如替换为 3.12 的自定义构建变体)。代码片段是根据你的实际设置生成的,因此应该可以直接使用,但如果需要,你可以自定义它(例如更改 Python.tgz文件的位置,以便可以远程下载而不是本地机器上)。 -
确保在你的
WORKSPACE文件中的python_init_repositories()的requirements参数中有关于你的 Python 版本的条目。例如,对于Python 3.13,它应该有类似于"3.13": "//build:requirements_lock_3_13.txt"的内容。 -
对于不稳定版本的 Python,可选择(但强烈建议)运行
bazel build //build:all_py_deps --repo_env=HERMETIC_PYTHON_VERSION="3.13",其中3.13是您在第三步构建的 Python 解释器版本。这将使pip从源代码拉取并构建 JAX 所有依赖的 Python 包(例如numpy、scipy、matplotlib、zstandard)。建议首先执行此步骤(即独立于实际 JAX 构建之外),以避免在构建 JAX 本身和其 Python 依赖项时发生冲突。例如,我们通常使用 clang 构建 JAX,但使用 clang 从源代码构建matplotlib由于 GCC 和 clang 在链接时优化行为(通过-flto标志触发的链接时优化)的差异而直接失败,默认情况下 matplotlib 默认假定 GCC。如果您针对稳定版本的 Python 进行构建,或者一般情况下不期望任何 Python 依赖项从源代码构建(即相应 Python 版本的二进制分发包已经存在于仓库中),则不需要执行此步骤。 -
恭喜,你已经为 JAX 项目构建和配置了自定义 Python!现在你可以像往常一样执行构建/测试命令,只需确保
HERMETIC_PYTHON_VERSION环境变量已设置并指向你的新版本。 -
注意,如果你正在构建 Python 的预发布版本,则更新
requirements_lock_<python_version>.txt文件以与新构建的 Python 匹配可能会失败,因为软件包仓库没有相应的二进制包。当没有二进制包可用时,pip-compile将继续从源代码构建,这可能会失败,因为其比在pip安装期间执行同样操作更为严格。建议为不稳定版本的 Python 更新要求锁定文件的方法是更新最新稳定版本(例如3.12)的要求(因此特殊的//build:requirements_dev.update目标),然后将结果复制到不稳定 Python 的锁定文件(例如3.13)中:
bazel run //build:requirements_dev.update --repo_env=HERMETIC_PYTHON_VERSION="3.12"
cp build/requirements_lock_3_12.txt build/requirements_lock_3_13.txt
bazel build //build:all_py_deps --repo_env=HERMETIC_PYTHON_VERSION="3.13"
# You may need to edit manually the resultant lock file, depending on how ready
# your dependencies are for the new version of Python.
安装 jax
安装完成 jaxlib 后,可以通过运行以下命令安装 jax:
pip install -e . # installs jax
要从 GitHub 升级到最新版本,只需从 JAX 仓库根目录运行 git pull,然后通过运行 build.py 或必要时升级 jaxlib 进行重新构建。你不应该需要重新安装 jax,因为 pip install -e 会设置从 site-packages 到仓库的符号链接。
运行测试
有两种支持的机制可以运行 JAX 测试,即使用 Bazel 或使用 pytest。
使用 Bazel
首先,通过运行以下命令配置 JAX 构建:
python build/build.py --configure_only
你可以向 build.py 传递额外选项以配置构建;请查看 jaxlib 构建文档获取详细信息。
默认情况下,Bazel 构建使用从源代码构建的 jaxlib 运行 JAX 测试。要运行 JAX 测试,请运行:
bazel test //tests:cpu_tests //tests:backend_independent_tests
如果您有必要的硬件,还可以使用//tests:gpu_tests和//tests:tpu_tests。
要使用预安装的jaxlib而不是构建它,您首先需要在 hermetic Python 中使其可用。要在 hermetic Python 中安装特定版本的jaxlib,请运行以下命令(以jaxlib >= 0.4.26为例):
echo -e "\njaxlib >= 0.4.26" >> build/requirements.in
python build/build.py --requirements_update
或者,要从本地 wheel 安装jaxlib(假设 Python 3.12):
echo -e "\n$(realpath jaxlib-0.4.26-cp312-cp312-manylinux2014_x86_64.whl)" >> build/requirements.in
python build/build.py --requirements_update --python_version=3.12
一旦在 hermetic 中安装了jaxlib,请运行:
bazel test --//jax:build_jaxlib=false //tests:cpu_tests //tests:backend_independent_tests
可以使用环境变量来控制多个测试行为(参见下文)。环境变量可以通过--test_env=FLAG=value标志传递给 Bazel 的 JAX 测试。
JAX 的一些测试适用于多个加速器(例如 GPU、TPU)。当 JAX 已安装时,您可以像这样运行 GPU 测试:
bazel test //tests:gpu_tests --local_test_jobs=4 --test_tag_filters=multiaccelerator --//jax:build_jaxlib=false --test_env=XLA_PYTHON_CLIENT_ALLOCATOR=platform
您可以通过在多个加速器上并行运行单个加速器测试来加速测试。这也会触发每个加速器的多个并发测试。对于 GPU,您可以像这样操作:
NB_GPUS=2
JOBS_PER_ACC=4
J=$((NB_GPUS * JOBS_PER_ACC))
MULTI_GPU="--run_under $PWD/build/parallel_accelerator_execute.sh --test_env=JAX_ACCELERATOR_COUNT=${NB_GPUS} --test_env=JAX_TESTS_PER_ACCELERATOR=${JOBS_PER_ACC} --local_test_jobs=$J"
bazel test //tests:gpu_tests //tests:backend_independent_tests --test_env=XLA_PYTHON_CLIENT_PREALLOCATE=false --test_tag_filters=-multiaccelerator $MULTI_GPU
使用pytest
首先,通过运行pip install -r build/test-requirements.txt安装依赖项。
使用pytest运行所有 JAX 测试时,建议使用pytest-xdist,它可以并行运行测试。它作为pip install -r build/test-requirements.txt命令的一部分安装。
从存储库根目录运行:
pytest -n auto tests
控制测试行为
JAX 以组合方式生成测试用例,您可以使用JAX_NUM_GENERATED_CASES环境变量控制为每个测试生成和检查的案例数(默认为 10)。自动化测试当前默认使用 25 个。
例如,可以这样编写
# Bazel
bazel test //tests/... --test_env=JAX_NUM_GENERATED_CASES=25`
或者
# pytest
JAX_NUM_GENERATED_CASES=25 pytest -n auto tests
自动化测试还使用默认的 64 位浮点数和整数运行测试(JAX_ENABLE_X64):
JAX_ENABLE_X64=1 JAX_NUM_GENERATED_CASES=25 pytest -n auto tests
您可以使用pytest的内置选择机制运行更具体的测试集,或者直接运行特定的测试文件以查看有关正在运行的案例的更详细信息:
JAX_NUM_GENERATED_CASES=5 python tests/lax_numpy_test.py
您可以通过传递环境变量JAX_SKIP_SLOW_TESTS=1来跳过一些已知的运行缓慢的测试。
要指定从测试文件运行的特定一组测试,您可以通过--test_targets标志传递字符串或正则表达式。例如,您可以使用以下命令运行jax.numpy.pad的所有测试:
python tests/lax_numpy_test.py --test_targets="testPad"
Colab 笔记本在文档构建过程中会进行错误测试。
Doctests
JAX 使用 pytest 以 doctest 模式测试文档中的代码示例。您可以使用以下命令运行:
pytest docs
另外,JAX 以doctest-modules模式运行 pytest,以确保函数文档字符串中的代码示例能够正确运行。例如,您可以在本地运行如下命令:
pytest --doctest-modules jax/_src/numpy/lax_numpy.py
请注意,当在完整包上运行 doctest 命令时,有几个文件被标记为跳过;您可以在ci-build.yaml中查看详细信息。
类型检查
我们使用 mypy 来检查类型提示。要像 CI 一样在本地检查类型:
pip install mypy
mypy --config=pyproject.toml --show-error-codes jax
或者,您可以使用 pre-commit 框架在 git 存储库中的所有暂存文件上运行此命令,自动使用与 GitHub CI 中相同的 mypy 版本:
pre-commit run mypy
代码检查
JAX 使用 ruff linter 来确保代码质量。您可以通过运行以下命令检查本地更改:
pip install ruff
ruff jax
或者,您可以使用 pre-commit 框架在 git 存储库中的所有暂存文件上运行此命令,自动使用与 GitHub 测试中相同的 ruff 版本:
pre-commit run ruff
更新文档
要重新构建文档,请安装几个包:
pip install -r docs/requirements.txt
然后运行:
sphinx-build -b html docs docs/build/html -j auto
这可能需要很长时间,因为它执行文档源中的许多笔记本;如果您希望在不执行笔记本的情况下构建文档,可以运行:
sphinx-build -b html -D nb_execution_mode=off docs docs/build/html -j auto
然后您可以在 docs/build/html/index.html 中看到生成的文档。
-j auto 选项控制构建的并行性。您可以使用数字替换 auto,以控制使用多少 CPU 核心。
更新笔记本
我们使用 jupytext 来维护 docs/notebooks 中笔记本的两个同步副本:一个是 ipynb 格式,另一个是 md 格式。前者的优点是可以直接在 Colab 中打开和执行;后者的优点是在版本控制中更容易跟踪差异。
编辑 ipynb
对于对代码和输出进行重大修改的大型更改,最简单的方法是在 Jupyter 或 Colab 中编辑笔记本。要在 Colab 界面中编辑笔记本,请打开 colab.research.google.com,从本地仓库上传。根据需要更新,Run all cells 然后 Download ipynb。您可能希望使用 sphinx-build 测试它是否正确执行,如上所述。
编辑 md
对于对笔记本文本内容进行较小更改的情况,最简单的方法是使用文本编辑器编辑 .md 版本。
同步笔记本
在编辑 ipynb 或 md 版本的笔记本后,您可以通过运行 jupytext --sync 来同步这两个版本的内容;例如:
pip install jupytext==1.16.0
jupytext --sync docs/notebooks/thinking_in_jax.ipynb
jupytext 版本应与 .pre-commit-config.yaml 中指定的版本匹配。
要检查 markdown 和 ipynb 文件是否正确同步,可以使用 pre-commit 框架执行与 github CI 相同的检查:
git add docs -u # pre-commit runs on files in git staging.
pre-commit run jupytext
创建新的笔记本
如果您要向文档添加新的笔记本,并希望使用此处讨论的 jupytext --sync 命令,可以通过以下命令设置您的笔记本以使用 jupytext:
jupytext --set-formats ipynb,md:myst path/to/the/notebook.ipynb
这是通过在笔记本文件中添加一个 "jupytext" 元数据字段来实现的,该字段指定了所需的格式,并在调用 jupytext --sync 命令时被识别。
Sphinx 构建内的笔记本
一些笔记本是作为预提交检查的一部分和作为 Read the docs 构建的一部分自动生成的。如果单元格引发错误,则构建将失败。如果错误是有意的,您可以捕获它们,或者将单元格标记为 raises-exceptions 元数据(示例 PR)。您必须在 .ipynb 文件中手动添加此元数据。当其他人重新保存笔记本时,它将被保留。
我们排除一些笔记本的构建,例如,因为它们包含长时间的计算。请参阅 conf.py 中的 exclude_patterns。
在 readthedocs.io 上构建文档
JAX 的自动生成文档位于 jax.readthedocs.io/。
整个项目的文档构建受 readthedocs JAX settings 的控制。当前的设置在代码推送到 GitHub 的 main 分支后会触发文档构建。对于每个代码版本,构建过程由 .readthedocs.yml 和 docs/conf.py 配置文件驱动。
对于每个自动化文档构建,您可以查看 documentation build logs。
如果您想在 Readthedocs 上测试文档生成,请将代码推送到 test-docs 分支。该分支也将自动构建,并且您可以在这里查看生成的文档 here。如果文档构建失败,您可能希望 清除 test-docs 的构建环境。
在本地测试中,我能够在一个全新的目录中通过重放我在 Readthedocs 日志中看到的命令来完成:
mkvirtualenv jax-docs # A new virtualenv
mkdir jax-docs # A new directory
cd jax-docs
git clone --no-single-branch --depth 50 https://github.com/google/jax
cd jax
git checkout --force origin/test-docs
git clean -d -f -f
workon jax-docs
python -m pip install --upgrade --no-cache-dir pip
python -m pip install --upgrade --no-cache-dir -I Pygments==2.3.1 setuptools==41.0.1 docutils==0.14 mock==1.0.1 pillow==5.4.1 alabaster>=0.7,<0.8,!=0.7.5 commonmark==0.8.1 recommonmark==0.5.0 'sphinx<2' 'sphinx-rtd-theme<0.5' 'readthedocs-sphinx-ext<1.1'
python -m pip install --exists-action=w --no-cache-dir -r docs/requirements.txt
cd docs
python `which sphinx-build` -T -E -b html -d _build/doctrees-readthedocs -D language=en . _build/html
Internal APIs
core
Jaxpr(constvars, invars, outvars, eqns[, …]) | |
|---|---|
ClosedJaxpr(jaxpr, consts) |
Autodidax:从头开始学习 JAX 核心
你是否想过学习 JAX 是如何工作的,但实现看起来深奥无比?那么,你很幸运!通过阅读本教程,你将了解 JAX 核心系统中的每一个重要思想。你甚至将了解我们奇怪的行话!
这是一个正在进行中的草稿。 这里还缺少一些重要的部分,将在第五部分和第六部分(以及更多?)中添加。此外,这里还有一些尚未应用于主系统的简化,但我们会应用的。
第一部分:转换作为解释器:标准评估、jvp和vmap
我们希望转换看起来像这样的函数:
def f(x):
y = sin(x) * 2.
z = - y + x
return z
将函数如sin和作为中缀操作符底层的算术运算(mul、add和neg)视为原语操作,意味着它们是处理的原子单位而不是组合。
“Transform”意味着“以不同方式解释”。我们不再采用标准解释,其中我们将原语操作应用于数值输入以生成数值输出,而是想要重写原语应用,并让不同的值流过我们的程序。例如,我们可能希望用其 JVP 规则的应用替换每个原语的应用,并让原始-切线对流经我们的程序。此外,我们希望能够组合多个转换,形成解释器的堆栈。
JAX 核心机制
我们可以实现解释器的堆栈,甚至可以在执行要转换的 Python 函数时实时执行它们。首先,让我们定义这些原语,以便我们可以拦截它们的应用:
from typing import NamedTuple
class Primitive(NamedTuple):
name: str
add_p = Primitive('add')
mul_p = Primitive('mul')
neg_p = Primitive("neg")
sin_p = Primitive("sin")
cos_p = Primitive("cos")
reduce_sum_p = Primitive("reduce_sum")
greater_p = Primitive("greater")
less_p = Primitive("less")
transpose_p = Primitive("transpose")
broadcast_p = Primitive("broadcast")
def add(x, y): return bind1(add_p, x, y)
def mul(x, y): return bind1(mul_p, x, y)
def neg(x): return bind1(neg_p, x)
def sin(x): return bind1(sin_p, x)
def cos(x): return bind1(cos_p, x)
def greater(x, y): return bind1(greater_p, x, y)
def less(x, y): return bind1(less_p, x, y)
def transpose(x, perm): return bind1(transpose_p, x, perm=perm)
def broadcast(x, shape, axes): return bind1(broadcast_p, x, shape=shape, axes=axes)
def reduce_sum(x, axis=None):
if axis is None:
axis = tuple(range(np.ndim(x)))
if type(axis) is int:
axis = (axis,)
return bind1(reduce_sum_p, x, axis=axis)
def bind1(prim, *args, **params):
out, = bind(prim, *args, **params)
return out
我们稍后将设置数组数据类型和中缀操作方法。
一个Primitive只是一个带有名称的对象,我们附加了我们的解释规则(每个转换对应一个规则)。bind函数是我们的拦截点:它将根据参数在跟踪器中的封装方式以及活动的解释器来确定应用哪个转换规则。
用户代码调用的函数,如add和sin,只是对bind调用的包装器。这些包装器允许我们控制参数如何传递给bind,特别是我们遵循一个方便的内部约定:当我们调用bind时,我们将表示数组数据的值作为位置参数传递,并通过关键字将元数据(如axis参数传递给sum_p)。这种调用约定简化了一些核心逻辑(因为例如下文将要定义的Tracer类的实例只能出现在bind的位置参数中)。这些包装器还可以提供文档字符串!
我们将活动解释器表示为堆栈。堆栈只是一个简单的list,每个元素是一个容器,具有整数级别(对应于元素在堆栈中的高度)、解释器类型(我们称之为trace_type)以及解释器需要的任何全局数据的可选字段。我们称每个元素为MainTrace,尽管“Interpreter”可能更加描述性。
from collections.abc import Sequence
from contextlib import contextmanager
from typing import Optional, Any
class MainTrace(NamedTuple):
level: int
trace_type: type['Trace']
global_data: Optional[Any]
trace_stack: list[MainTrace] = []
dynamic_trace: Optional[MainTrace] = None # to be employed in Part 3
@contextmanager
def new_main(trace_type: type['Trace'], global_data=None):
level = len(trace_stack)
main = MainTrace(level, trace_type, global_data)
trace_stack.append(main)
try:
yield main
finally:
trace_stack.pop()
在我们准备应用变换时,我们将使用new_main将另一个解释器推送到堆栈上。然后,在函数中应用原语时,我们可以认为bind首先由堆栈顶部的追踪器解释(即具有最高级别的追踪器)。如果第一个解释器本身在其对于原语的解释规则中绑定其他原语,例如sin_p的 JVP 规则可能绑定cos_p和mul_p,那么这些bind调用将由下一个级别的解释器处理。
解释器堆栈的底部放什么?在底部,我们知道所有变换解释器都已完成,我们只想进行标准评估。因此,在底部我们将放置一个评估解释器。
让我们概述一下解释器的接口,它基于Trace和Tracer基类。Tracer表示一个封装的值,可能携带一些由解释器使用的额外上下文数据。Trace处理将值封装到Tracer中,并且还处理原语应用。
class Trace:
main: MainTrace
def __init__(self, main: MainTrace) -> None:
self.main = main
def pure(self, val): assert False # must override
def lift(self, val): assert False # must override
def process_primitive(self, primitive, tracers, params):
assert False # must override
前两种方法是关于在Tracer中封装值,Tracer是我们转换的 Python 程序中流动的对象。最后一种方法是我们将用于解释原始应用的回调。
Trace本身除了引用其对应的MainTrace实例之外并不包含任何数据。事实上,在应用变换过程中可能会创建和丢弃多个Trace实例,而每个应用变换只会创建一个MainTrace实例。
至于Tracer们本身,每个Tracer都携带一个抽象值(并将中缀运算符转发给它),其余由变换决定。(Tracer与AbstractValue之间的关系是每个变换对应一个Tracer,并且每个基本类型(如数组)至少有一个AbstractValue。)
import numpy as np
class Tracer:
_trace: Trace
__array_priority__ = 1000
@property
def aval(self):
assert False # must override
def full_lower(self):
return self # default implementation
def __neg__(self): return self.aval._neg(self)
def __add__(self, other): return self.aval._add(self, other)
def __radd__(self, other): return self.aval._radd(self, other)
def __mul__(self, other): return self.aval._mul(self, other)
def __rmul__(self, other): return self.aval._rmul(self, other)
def __gt__(self, other): return self.aval._gt(self, other)
def __lt__(self, other): return self.aval._lt(self, other)
def __bool__(self): return self.aval._bool(self)
def __nonzero__(self): return self.aval._nonzero(self)
def __getattr__(self, name):
try:
return getattr(self.aval, name)
except AttributeError:
raise AttributeError(f"{self.__class__.__name__} has no attribute {name}")
def swap(f): return lambda x, y: f(y, x)
class ShapedArray:
array_abstraction_level = 1
shape: tuple[int, ...]
dtype: np.dtype
def __init__(self, shape, dtype):
self.shape = shape
self.dtype = dtype
@property
def ndim(self):
return len(self.shape)
_neg = staticmethod(neg)
_add = staticmethod(add)
_radd = staticmethod(swap(add))
_mul = staticmethod(mul)
_rmul = staticmethod(swap(mul))
_gt = staticmethod(greater)
_lt = staticmethod(less)
@staticmethod
def _bool(tracer):
raise Exception("ShapedArray can't be unambiguously converted to bool")
@staticmethod
def _nonzero(tracer):
raise Exception("ShapedArray can't be unambiguously converted to bool")
def str_short(self):
return f'{self.dtype.name}[{",".join(str(d) for d in self.shape)}]'
def __hash__(self):
return hash((self.shape, self.dtype))
def __eq__(self, other):
return (type(self) is type(other) and
self.shape == other.shape and self.dtype == other.dtype)
def __repr__(self):
return f"ShapedArray(shape={self.shape}, dtype={self.dtype})"
class ConcreteArray(ShapedArray):
array_abstraction_level = 2
val: np.ndarray
def __init__(self, val):
self.val = val
self.shape = val.shape
self.dtype = val.dtype
@staticmethod
def _bool(tracer):
return bool(tracer.aval.val)
@staticmethod
def _nonzero(tracer):
return bool(tracer.aval.val)
def get_aval(x):
if isinstance(x, Tracer):
return x.aval
elif type(x) in jax_types:
return ConcreteArray(np.asarray(x))
else:
raise TypeError(x)
jax_types = {bool, int, float,
np.bool_, np.int32, np.int64, np.float32, np.float64, np.ndarray}
注意,实际上我们为数组有两个AbstractValue,代表不同的抽象级别。ShapedArray代表具有给定形状和 dtype 的所有可能数组的集合。ConcreteArray代表一个由单个数组值组成的单例集。
现在我们已经设置了解释器堆栈、解释器的 Trace/Tracer API 和抽象值,我们可以回来实现bind了:
def bind(prim, *args, **params):
top_trace = find_top_trace(args)
tracers = [full_raise(top_trace, arg) for arg in args]
outs = top_trace.process_primitive(prim, tracers, params)
return [full_lower(out) for out in outs]
主要的操作是我们调用find_top_trace来找出哪个解释器应该处理这个基元应用。然后我们调用该顶层跟踪的process_primitive,以便跟踪可以应用其解释规则。full_raise的调用只是确保输入封装在顶层跟踪的Tracer实例中,而对full_lower的调用是一个可选的优化,以便我们尽可能多地从Tracer中解封值。
import operator as op
def find_top_trace(xs) -> Trace:
top_main = max((x._trace.main for x in xs if isinstance(x, Tracer)),
default=trace_stack[0], key=op.attrgetter('level'))
if dynamic_trace and dynamic_trace.level > top_main.level:
top_main = dynamic_trace
return top_main.trace_type(top_main)
换句话说,忽略dynamic_trace步骤直到第三部分,find_top_trace返回与其输入上的Tracer相关联的最高级解释器,并且否则返回堆栈底部的解释器(至少目前总是一个求值跟踪)。这与上面的描述有所偏离,我们总是从运行堆栈顶部的解释器开始,然后逐级向下工作,应用堆栈中的每个解释器。相反,我们只有在将输入参数传递给基元绑定的Tracer中时才应用解释器对应的解释器时才应用解释器。这种优化让我们可以跳过不相关的转换,但内置了一个假设,即转换大部分时候都遵循数据依赖性(除了特殊的堆栈底部解释器,它解释一切)。
另一种方法是使堆栈中的每个解释器都解释每个操作。值得探索!JAX 大部分是围绕数据依赖性而设计的,大部分原因是因为这对于自动微分来说非常自然,而 JAX 的根源在于自动微分。但也许会过拟合。
def full_lower(val: Any):
if isinstance(val, Tracer):
return val.full_lower()
else:
return val
def full_raise(trace: Trace, val: Any) -> Tracer:
if not isinstance(val, Tracer):
assert type(val) in jax_types
return trace.pure(val)
level = trace.main.level
if val._trace.main is trace.main:
return val
elif val._trace.main.level < level:
return trace.lift(val)
elif val._trace.main.level > level:
raise Exception(f"Can't lift level {val._trace.main.level} to {level}.")
else: # val._trace.level == level
raise Exception(f"Different traces at same level: {val._trace}, {trace}.")
full_raise中的逻辑用于将值封装在特定Trace的Tracer中,根据上下文对Trace调用不同的方法:对非Tracer常数调用Trace.pure,对已经来自低级解释器的Tracer调用Trace.lift。这两种方法可以共享相同的实现,但通过在核心逻辑中加以区分,我们可以向Trace子类提供更多信息。
JAX 核心就是这样!现在我们可以开始添加解释器了。
评估解释器
我们将从最简单的解释器开始:位于解释器堆栈底部的评估解释器。
class EvalTrace(Trace):
pure = lift = lambda self, x: x # no boxing in Tracers needed
def process_primitive(self, primitive, tracers, params):
return impl_rulesprimitive
trace_stack.append(MainTrace(0, EvalTrace, None)) # special bottom of the stack
# NB: in JAX, instead of a dict we attach impl rules to the Primitive instance
impl_rules = {}
impl_rules[add_p] = lambda x, y: [np.add(x, y)]
impl_rules[mul_p] = lambda x, y: [np.multiply(x, y)]
impl_rules[neg_p] = lambda x: [np.negative(x)]
impl_rules[sin_p] = lambda x: [np.sin(x)]
impl_rules[cos_p] = lambda x: [np.cos(x)]
impl_rules[reduce_sum_p] = lambda x, *, axis: [np.sum(x, axis)]
impl_rules[greater_p] = lambda x, y: [np.greater(x, y)]
impl_rules[less_p] = lambda x, y: [np.less(x, y)]
impl_rules[transpose_p] = lambda x, *, perm: [np.transpose(x, perm)]
def broadcast_impl(x, *, shape, axes):
for axis in sorted(axes):
x = np.expand_dims(x, axis)
return [np.broadcast_to(x, shape)]
impl_rules[broadcast_p] = broadcast_impl
有了这个解释器,我们可以评估用户函数:
def f(x):
y = sin(x) * 2.
z = - y + x
return z
print(f(3.0))
2.7177599838802657
哇!就像在一个大圈子里转圈。但这种间接性的关键在于现在我们可以添加一些真正的转换。
带有jvp的前向模式自动微分
首先,一些辅助函数:
import builtins
def zeros_like(val):
aval = get_aval(val)
return np.zeros(aval.shape, aval.dtype)
def unzip2(pairs):
lst1, lst2 = [], []
for x1, x2 in pairs:
lst1.append(x1)
lst2.append(x2)
return lst1, lst2
def map(f, *xs):
return list(builtins.map(f, *xs))
def zip(*args):
fst, *rest = args = map(list, args)
n = len(fst)
for arg in rest:
assert len(arg) == n
return list(builtins.zip(*args))
前向模式自动微分的Tracer携带原始-切线对。Trace应用 JVP 规则。
class JVPTracer(Tracer):
def __init__(self, trace, primal, tangent):
self._trace = trace
self.primal = primal
self.tangent = tangent
@property
def aval(self):
return get_aval(self.primal)
class JVPTrace(Trace):
pure = lift = lambda self, val: JVPTracer(self, val, zeros_like(val))
def process_primitive(self, primitive, tracers, params):
primals_in, tangents_in = unzip2((t.primal, t.tangent) for t in tracers)
jvp_rule = jvp_rules[primitive]
primal_outs, tangent_outs = jvp_rule(primals_in, tangents_in, **params)
return [JVPTracer(self, x, t) for x, t in zip(primal_outs, tangent_outs)]
jvp_rules = {}
注意pure和lift都将一个值打包成一个带有最小上下文的JVPTracer,这是一个零切线值。
让我们添加一些用于原始函数的 JVP 规则:
def add_jvp(primals, tangents):
(x, y), (x_dot, y_dot) = primals, tangents
return [x + y], [x_dot + y_dot]
jvp_rules[add_p] = add_jvp
def mul_jvp(primals, tangents):
(x, y), (x_dot, y_dot) = primals, tangents
return [x * y], [x_dot * y + x * y_dot]
jvp_rules[mul_p] = mul_jvp
def sin_jvp(primals, tangents):
(x,), (x_dot,) = primals, tangents
return [sin(x)], [cos(x) * x_dot]
jvp_rules[sin_p] = sin_jvp
def cos_jvp(primals, tangents):
(x,), (x_dot,) = primals, tangents
return [cos(x)], [-sin(x) * x_dot]
jvp_rules[cos_p] = cos_jvp
def neg_jvp(primals, tangents):
(x,), (x_dot,) = primals, tangents
return [neg(x)], [neg(x_dot)]
jvp_rules[neg_p] = neg_jvp
def reduce_sum_jvp(primals, tangents, *, axis):
(x,), (x_dot,) = primals, tangents
return [reduce_sum(x, axis)], [reduce_sum(x_dot, axis)]
jvp_rules[reduce_sum_p] = reduce_sum_jvp
def greater_jvp(primals, tangents):
(x, y), _ = primals, tangents
out_primal = greater(x, y)
return [out_primal], [zeros_like(out_primal)]
jvp_rules[greater_p] = greater_jvp
def less_jvp(primals, tangents):
(x, y), _ = primals, tangents
out_primal = less(x, y)
return [out_primal], [zeros_like(out_primal)]
jvp_rules[less_p] = less_jvp
最后,我们添加一个转换 API 来启动跟踪:
def jvp_v1(f, primals, tangents):
with new_main(JVPTrace) as main:
trace = JVPTrace(main)
tracers_in = [JVPTracer(trace, x, t) for x, t in zip(primals, tangents)]
out = f(*tracers_in)
tracer_out = full_raise(trace, out)
primal_out, tangent_out = tracer_out.primal, tracer_out.tangent
return primal_out, tangent_out
而有着,我们可以进行区分!
x = 3.0
y, sin_deriv_at_3 = jvp_v1(sin, (x,), (1.0,))
print(sin_deriv_at_3)
print(cos(3.0))
-0.9899924966004454
-0.9899924966004454
def f(x):
y = sin(x) * 2.
z = - y + x
return z
x, xdot = 3., 1.
y, ydot = jvp_v1(f, (x,), (xdot,))
print(y)
print(ydot)
2.7177599838802657
2.979984993200891
def deriv(f):
return lambda x: jvp_v1(f, (x,), (1.,))[1]
print(deriv(sin)(3.))
print(deriv(deriv(sin))(3.))
print(deriv(deriv(deriv(sin)))(3.))
print(deriv(deriv(deriv(deriv(sin))))(3.))
-0.9899924966004454
-0.1411200080598672
0.9899924966004454
0.1411200080598672
def f(x):
if x > 0.: # Python control flow
return 2. * x
else:
return x
print(deriv(f)(3.))
print(deriv(f)(-3.))
2.0
1.0
Pytrees 和展平用户函数的输入和输出
jvp_v1 的一个限制是它假设用户函数接受数组作为位置参数并生成单个数组作为输出。如果它生成一个列表作为输出怎么办?或者接受嵌套容器作为输入?在每一层处理堆栈时处理所有可能的容器将会很麻烦。相反,我们可以包装用户函数,使得包装版本接受数组作为输入并返回一个扁平的数组列表作为输出。包装器只需展开其输入,调用用户函数,并展平输出。
下面是我们希望编写 jvp 的方式,假设用户总是给我们采用数组作为输入并生成扁平数组列表作为输出的函数:
def jvp_flat(f, primals, tangents):
with new_main(JVPTrace) as main:
trace = JVPTrace(main)
tracers_in = [JVPTracer(trace, x, t) for x, t in zip(primals, tangents)]
outs = f(*tracers_in)
tracers_out = [full_raise(trace, out) for out in outs]
primals_out, tangents_out = unzip2((t.primal, t.tangent) for t in tracers_out)
return primals_out, tangents_out
为了支持具有任意容器输入和输出的用户函数,下面是我们如何编写用户界面的 jvp 包装器:
def jvp(f, primals, tangents):
primals_flat, in_tree = tree_flatten(primals)
tangents_flat, in_tree2 = tree_flatten(tangents)
if in_tree != in_tree2: raise TypeError
f, out_tree = flatten_fun(f, in_tree)
primals_out_flat, tangents_out_flat = jvp_flat(f, primals_flat, tangents_flat)
primals_out = tree_unflatten(out_tree(), primals_out_flat)
tangents_out = tree_unflatten(out_tree(), tangents_out_flat)
return primals_out, tangents_out
注意,我们必须将用户函数输出的树结构信息传递回 flatten_fun 的调用者。这些信息在我们实际运行用户函数之前是不可用的,因此 flatten_fun 只返回一个可变单元的引用,表示为一个惰性求值体。这些副作用是安全的,因为我们总是精确地运行用户函数一次。(这种安全的制度是 linear_util.py 中“linear”名称的原因,以 线性类型 的意义上)
唯一剩下的是编写 tree_flatten、tree_unflatten 和 flatten_fun。
def flatten_fun(f, in_tree):
store = Store()
def flat_fun(*args_flat):
pytree_args = tree_unflatten(in_tree, args_flat)
out = f(*pytree_args)
out_flat, out_tree = tree_flatten(out)
store.set_value(out_tree)
return out_flat
return flat_fun, store
class Empty: pass
empty = Empty()
class Store:
val = empty
def set_value(self, val):
assert self.val is empty
self.val = val
def __call__(self):
return self.val
```</details> <details class="hide above-input"><summary aria-label="Toggle hidden content">显示代码单元源代码 隐藏代码单元源代码</summary>
```py
from collections.abc import Hashable, Iterable, Iterator
import itertools as it
from typing import Callable
class NodeType(NamedTuple):
name: str
to_iterable: Callable
from_iterable: Callable
def register_pytree_node(ty: type, to_iter: Callable, from_iter: Callable
) -> None:
node_types[ty] = NodeType(str(ty), to_iter, from_iter)
node_types: dict[type, NodeType] = {}
register_pytree_node(tuple, lambda t: (None, t), lambda _, xs: tuple(xs))
register_pytree_node(list, lambda l: (None, l), lambda _, xs: list(xs))
register_pytree_node(dict,
lambda d: map(tuple, unzip2(sorted(d.items()))),
lambda keys, vals: dict(zip(keys, vals)))
class PyTreeDef(NamedTuple):
node_type: NodeType
node_metadata: Hashable
child_treedefs: tuple['PyTreeDef', ...]
class Leaf: pass
leaf = Leaf()
def tree_flatten(x: Any) -> tuple[list[Any], PyTreeDef]:
children_iter, treedef = _tree_flatten(x)
return list(children_iter), treedef
def _tree_flatten(x: Any) -> tuple[Iterable, PyTreeDef]:
node_type = node_types.get(type(x))
if node_type:
node_metadata, children = node_type.to_iterable(x)
children_flat, child_trees = unzip2(map(_tree_flatten, children))
flattened = it.chain.from_iterable(children_flat)
return flattened, PyTreeDef(node_type, node_metadata, tuple(child_trees))
else:
return [x], leaf
def tree_unflatten(treedef: PyTreeDef, xs: list[Any]) -> Any:
return _tree_unflatten(treedef, iter(xs))
def _tree_unflatten(treedef: PyTreeDef, xs: Iterator) -> Any:
if treedef is leaf:
return next(xs)
else:
children = (_tree_unflatten(t, xs) for t in treedef.child_treedefs)
return treedef.node_type.from_iterable(treedef.node_metadata, children)
```</details>
通过这个处理 `jvp` 的 pytree 实现,我们现在可以处理任意输入和输出容器。这将在将来的转换中非常有用!
```py
def f(x):
y = sin(x) * 2.
z = - y + x
return {'hi': z, 'there': [x, y]}
x, xdot = 3., 1.
y, ydot = jvp(f, (x,), (xdot,))
print(y)
print(ydot)
{'hi': np.float64(2.7177599838802657), 'there': [3.0, np.float64(0.2822400161197344)]}
{'hi': np.float64(2.979984993200891), 'there': [1.0, np.float64(-1.9799849932008908)]}
使用 vmap 进行向量化批处理
首先是一对辅助函数,一个用于从未映射的抽象值生成映射的抽象值(通过移除一个轴),另一个用于在批处理维度之间移动:
def mapped_aval(batch_dim, aval):
shape = list(aval.shape)
del shape[batch_dim]
return ShapedArray(tuple(shape), aval.dtype)
def move_batch_axis(axis_size, src, dst, x):
if src is not_mapped:
target_shape = list(np.shape(x))
target_shape.insert(dst, axis_size)
return broadcast(x, target_shape, [dst])
elif src == dst:
return x
else:
return moveaxis(x, src, dst)
def moveaxis(x, src: int, dst: int):
perm = [i for i in range(np.ndim(x)) if i != src]
perm.insert(dst, src)
return transpose(x, perm)
用于向量化批处理的 Tracer 携带一个批处理值和一个可选整数,指示批处理轴(如果有的话)。
from typing import Union
class NotMapped: pass
not_mapped = NotMapped()
BatchAxis = Union[NotMapped, int]
class BatchTracer(Tracer):
def __init__(self, trace, val, batch_dim: BatchAxis):
self._trace = trace
self.val = val
self.batch_dim = batch_dim
@property
def aval(self):
if self.batch_dim is not_mapped:
return get_aval(self.val)
else:
return mapped_aval(self.batch_dim, get_aval(self.val))
def full_lower(self):
if self.batch_dim is not_mapped:
return full_lower(self.val)
else:
return self
class BatchTrace(Trace):
pure = lift = lambda self, val: BatchTracer(self, val, not_mapped)
def process_primitive(self, primitive, tracers, params):
vals_in, bdims_in = unzip2((t.val, t.batch_dim) for t in tracers)
vmap_rule = vmap_rules[primitive]
val_outs, bdim_outs = vmap_rule(self.axis_size, vals_in, bdims_in, **params)
return [BatchTracer(self, x, bd) for x, bd in zip(val_outs, bdim_outs)]
@property
def axis_size(self):
return self.main.global_data
vmap_rules = {}
在这里,我们实现了可选的 Tracer.full_lower 方法,这让我们能够在不需要的情况下去除批处理跟踪器,因为它不代表批处理值。
对于 BatchTrace,类似于 JVPTrace,pure 和 lift 方法只是将一个值装箱在 BatchTracer 中,并且只提供最少的上下文,这种情况下是一个采用 not_mapped 作为标志值的 batch_dim。请注意,我们使用 MainTrace 的解释器全局数据字段来存储批处理轴的大小。
接下来,我们可以为每个原语定义批处理解释器规则:
from functools import partial
def binop_batching_rule(op, axis_size, vals_in, dims_in):
(x, y), (x_bdim, y_bdim) = vals_in, dims_in
if x_bdim != y_bdim:
if x_bdim is not_mapped:
x = move_batch_axis(axis_size, x_bdim, y_bdim, x)
x_bdim = y_bdim
else:
y = move_batch_axis(axis_size, y_bdim, x_bdim, y)
return [op(x, y)], [x_bdim]
vmap_rules[add_p] = partial(binop_batching_rule, add)
vmap_rules[mul_p] = partial(binop_batching_rule, mul)
def vectorized_unop_batching_rule(op, axis_size, vals_in, dims_in):
(x,), (x_bdim,) = vals_in, dims_in
return [op(x)], [x_bdim]
vmap_rules[sin_p] = partial(vectorized_unop_batching_rule, sin)
vmap_rules[cos_p] = partial(vectorized_unop_batching_rule, cos)
vmap_rules[neg_p] = partial(vectorized_unop_batching_rule, neg)
def reduce_sum_batching_rule(axis_size, vals_in, dims_in, *, axis):
(x,), (x_bdim,) = vals_in, dims_in
new_axis = tuple(ax + (x_bdim <= ax) for ax in axis)
out_bdim = x_bdim - sum(ax < x_bdim for ax in axis)
return [reduce_sum(x, new_axis)], [out_bdim]
vmap_rules[reduce_sum_p] = reduce_sum_batching_rule
最后,我们添加了一个转换 API 来启动跟踪:
def vmap_flat(f, in_axes, *args):
axis_size, = {x.shape[ax] for x, ax in zip(args, in_axes)
if ax is not not_mapped}
with new_main(BatchTrace, axis_size) as main:
trace = BatchTrace(main)
tracers_in = [BatchTracer(trace, x, ax) if ax is not None else x
for x, ax in zip(args, in_axes)]
outs = f(*tracers_in)
tracers_out = [full_raise(trace, out) for out in outs]
vals_out, bdims_out = unzip2((t.val, t.batch_dim) for t in tracers_out)
outs_transposed = [move_batch_axis(axis_size, bdim, 0, val_out)
for val_out, bdim in zip(vals_out, bdims_out)]
return outs_transposed
def vmap(f, in_axes):
def batched_f(*args):
args_flat, in_tree = tree_flatten(args)
in_axes_flat, in_tree2 = tree_flatten(in_axes)
if in_tree != in_tree2: raise TypeError
f_flat, out_tree = flatten_fun(f, in_tree)
outs_flat = vmap_flat(f_flat, in_axes_flat, *args_flat)
return tree_unflatten(out_tree(), outs_flat)
return batched_f
def add_one_to_a_scalar(scalar):
assert np.ndim(scalar) == 0
return 1 + scalar
vector_in = np.arange(3.)
vector_out = vmap(add_one_to_a_scalar, (0,))(vector_in)
print(vector_in)
print(vector_out)
[0\. 1\. 2.]
[1\. 2\. 3.]
def jacfwd(f, x):
pushfwd = lambda v: jvp(f, (x,), (v,))[1]
vecs_in = np.eye(np.size(x)).reshape(np.shape(x) * 2)
return vmap(pushfwd, (0,))(vecs_in)
def f(x):
return sin(x)
jacfwd(f, np.arange(3.))
array([[ 1\. , 0\. , -0\. ],
[ 0\. , 0.54030231, -0\. ],
[ 0\. , 0\. , -0.41614684]])
这就是关于 jvp 和 vmap 的全部内容!
第二部分:Jaxprs
下一个即将到来的转换是jit用于即时编译,以及vjp用于反向模式自动微分。(grad仅仅是vjp的一个小包装器。) 而jvp和vmap只需要每个Tracer携带一点额外的上下文,对于jit和vjp,我们需要更丰富的上下文:我们需要代表程序。也就是说,我们需要 jaxprs!
Jaxprs 是 JAX 的内部程序的中间表示。它们是显式类型化的、功能性的、一阶的,并且处于 ANF 形式。因为jit的目的是将计算分阶段出 Python,所以我们需要一个程序表示。对于任何我们想要分阶段的计算,我们需要能够将其表示为数据,并且在追踪 Python 函数时逐步构建它。类似地,vjp需要一种方法来表示反向模式自动微分的后向传播计算。我们为这两个需求使用相同的 jaxpr 程序表示。
(构建程序表示是最free种类的追踪转换,因此除了处理本地 Python 控制流问题外,任何转换都可以通过首先追踪到 jaxpr,然后解释 jaxpr 来实现。)
Jaxpr 数据结构
jaxpr 术语的语法大致为:
jaxpr ::=
{ lambda <binder> , ... .
let <eqn>
...
in ( <atom> , ... ) }
binder ::= <var>:<array_type>
var ::= a | b | c | ...
atom ::= <var> | <literal>
literal ::= <int32> | <int64> | <float32> | <float64>
eqn ::= <binder> , ... = <primitive> [ <params> ] <atom> , ...
类型的语法如下:
jaxpr_type ::= [ <array_type> , ... ] -> [ <array_type> , ... ]
array_type ::= <dtype>[<shape>]
dtype ::= f32 | f64 | i32 | i64
shape ::= <int> , ...
我们如何将这些表示为 Python 数据结构?我们重复使用 ShapedArrays 来表示类型,并且可以用几个 Python 结构来表示术语语法:
class Var:
aval: ShapedArray
def __init__(self, aval): self.aval = aval
class Lit:
val: Any
aval: ShapedArray
def __init__(self, val):
self.aval = aval = raise_to_shaped(get_aval(val))
self.val = np.array(val, aval.dtype)
Atom = Union[Var, Lit]
class JaxprEqn(NamedTuple):
primitive: Primitive
inputs: list[Atom]
params: dict[str, Any]
out_binders: list[Var]
class Jaxpr(NamedTuple):
in_binders: list[Var]
eqns: list[JaxprEqn]
outs: list[Atom]
def __hash__(self): return id(self)
__eq__ = op.is_
def raise_to_shaped(aval):
return ShapedArray(aval.shape, aval.dtype)
对 jaxpr 进行类型检查涉及检查是否存在未绑定的变量,变量是否仅绑定一次,以及每个方程的原始应用类型是否与输出绑定器的类型匹配。
class JaxprType(NamedTuple):
in_types: list[ShapedArray]
out_types: list[ShapedArray]
def __repr__(self):
in_types = ', '.join(aval.str_short() for aval in self.in_types)
out_types = ', '.join(aval.str_short() for aval in self.out_types)
return f'({in_types}) -> ({out_types})'
def typecheck_jaxpr(jaxpr: Jaxpr) -> JaxprType:
env: set[Var] = set()
for v in jaxpr.in_binders:
if v in env: raise TypeError
env.add(v)
for eqn in jaxpr.eqns:
in_types = [typecheck_atom(env, x) for x in eqn.inputs]
out_types = abstract_eval_ruleseqn.primitive
for out_binder, out_type in zip(eqn.out_binders, out_types):
if not out_type == out_binder.aval: raise TypeError
for out_binder in eqn.out_binders:
if out_binder in env: raise TypeError
env.add(out_binder)
in_types = [v.aval for v in jaxpr.in_binders]
out_types = [typecheck_atom(env, x) for x in jaxpr.outs]
return JaxprType(in_types, out_types)
def typecheck_atom(env: set[Var], x: Atom) -> ShapedArray:
if isinstance(x, Var):
if x not in env: raise TypeError("unbound variable")
return x.aval
elif isinstance(x, Lit):
return raise_to_shaped(get_aval(x.val))
else:
assert False
我们可以使用一个简单的解释器将 jaxpr 表示的函数应用于参数。
def eval_jaxpr(jaxpr: Jaxpr, args: list[Any]) -> list[Any]:
env: dict[Var, Any] = {}
def read(x: Atom) -> Any:
return env[x] if type(x) is Var else x.val
def write(v: Var, val: Any) -> None:
assert v not in env # single-assignment
env[v] = val
map(write, jaxpr.in_binders, args)
for eqn in jaxpr.eqns:
in_vals = map(read, eqn.inputs)
outs = bind(eqn.primitive, *in_vals, **eqn.params)
map(write, eqn.out_binders, outs)
return map(read, jaxpr.outs)
def jaxpr_as_fun(jaxpr: Jaxpr):
return lambda *args: eval_jaxpr(jaxpr, args)
通过在解释器中使用bind,这个解释器本身是可追踪的。
使用追踪构建 jaxprs
现在我们有了 jaxprs 作为一个数据结构,我们需要从追踪 Python 代码产生它们的方法。一般来说,我们追踪到 jaxpr 有两种变体;jit使用其中一种,而vjp使用另一种。我们将从jit使用的变体开始,这也被控制流原语如lax.cond、lax.while_loop和lax.scan所使用。
def split_list(lst: list[Any], n: int) -> tuple[list[Any], list[Any]]:
assert 0 <= n <= len(lst)
return lst[:n], lst[n:]
def partition_list(bs: list[bool], l: list[Any]) -> tuple[list[Any], list[Any]]:
assert len(bs) == len(l)
lists = lst1, lst2 = [], []
for b, x in zip(bs, l):
lists[b].append(x)
return lst1, lst2
# NB: the analogous class in JAX is called 'DynamicJaxprTracer'
class JaxprTracer(Tracer):
__slots__ = ['aval']
aval: ShapedArray
def __init__(self, trace, aval):
self._trace = trace
self.aval = aval
# NB: the analogous class in JAX is called 'DynamicJaxprTrace'
class JaxprTrace(Trace):
def new_arg(self, aval: ShapedArray) -> JaxprTracer:
aval = raise_to_shaped(aval)
tracer = self.builder.new_tracer(self, aval)
self.builder.tracer_to_var[id(tracer)] = Var(aval)
return tracer
def get_or_make_const_tracer(self, val: Any) -> JaxprTracer:
tracer = self.builder.const_tracers.get(id(val))
if tracer is None:
tracer = self.builder.new_tracer(self, raise_to_shaped(get_aval(val)))
self.builder.add_const(tracer, val)
return tracer
pure = lift = get_or_make_const_tracer
def process_primitive(self, primitive, tracers, params):
avals_in = [t.aval for t in tracers]
avals_out = abstract_eval_rulesprimitive
out_tracers = [self.builder.new_tracer(self, a) for a in avals_out]
inputs = [self.builder.getvar(t) for t in tracers]
outvars = [self.builder.add_var(t) for t in out_tracers]
self.builder.add_eqn(JaxprEqn(primitive, inputs, params, outvars))
return out_tracers
@property
def builder(self):
return self.main.global_data
# NB: in JAX, we instead attach abstract eval rules to Primitive instances
abstract_eval_rules = {}
注意,我们在解释器全局数据中保持一个构建器对象,该对象跟踪变量、常量和等式,随着我们构建 jaxpr 而逐步积累。
class JaxprBuilder:
eqns: list[JaxprEqn]
tracer_to_var: dict[int, Var]
const_tracers: dict[int, JaxprTracer]
constvals: dict[Var, Any]
tracers: list[JaxprTracer]
def __init__(self):
self.eqns = []
self.tracer_to_var = {}
self.const_tracers = {}
self.constvals = {}
self.tracers = []
def new_tracer(self, trace: JaxprTrace, aval: ShapedArray) -> JaxprTracer:
tracer = JaxprTracer(trace, aval)
self.tracers.append(tracer)
return tracer
def add_eqn(self, eqn: JaxprEqn) -> None:
self.eqns.append(eqn)
def add_var(self, tracer: JaxprTracer) -> Var:
assert id(tracer) not in self.tracer_to_var
var = self.tracer_to_var[id(tracer)] = Var(tracer.aval)
return var
def getvar(self, tracer: JaxprTracer) -> Var:
var = self.tracer_to_var.get(id(tracer))
assert var is not None
return var
def add_const(self, tracer: JaxprTracer, val: Any) -> Var:
var = self.add_var(tracer)
self.const_tracers[id(val)] = tracer
self.constvals[var] = val
return var
def build(self, in_tracers: list[JaxprTracer], out_tracers: list[JaxprTracer]
) -> tuple[Jaxpr, list[Any]]:
constvars, constvals = unzip2(self.constvals.items())
t2v = lambda t: self.tracer_to_var[id(t)]
in_binders = constvars + [t2v(t) for t in in_tracers]
out_vars = [t2v(t) for t in out_tracers]
jaxpr = Jaxpr(in_binders, self.eqns, out_vars)
typecheck_jaxpr(jaxpr)
jaxpr, constvals = _inline_literals(jaxpr, constvals)
return jaxpr, constvals
def _inline_literals(jaxpr: Jaxpr, consts: list[Any]) -> tuple[Jaxpr, list[Any]]:
const_binders, other_binders = split_list(jaxpr.in_binders, len(consts))
scalars = [type(x) in jax_types and not get_aval(x).shape for x in consts]
new_const_binders, lit_binders = partition_list(scalars, const_binders)
new_consts, lit_vals = partition_list(scalars, consts)
literals = dict(zip(lit_binders, map(Lit, lit_vals)))
new_eqns = [JaxprEqn(eqn.primitive, [literals.get(x, x) for x in eqn.inputs],
eqn.params, eqn.out_binders) for eqn in jaxpr.eqns]
new_outs = [literals.get(x, x) for x in jaxpr.outs]
new_jaxpr = Jaxpr(new_const_binders + other_binders, new_eqns, new_outs)
typecheck_jaxpr(new_jaxpr)
return new_jaxpr, new_consts
我们需要JaxprTrace.process_primitive的规则基本上是原始应用的类型规则:给定原始应用、其参数和输入的类型,规则必须生成一个输出类型,然后与输出的JaxprTracer一起打包。我们可以使用抽象评估规则来实现相同的目的,尽管它们可能更加通用(因为抽象评估规则必须接受 ConcreteArray 输入,并且因为它们只需返回可能输出集的上限,它们也可以生成 ConcreteArray 输出)。我们将重用这些抽象评估规则用于其他生成 jaxpr 的跟踪机制,其中额外的通用性是有用的。
def binop_abstract_eval(x: ShapedArray, y: ShapedArray) -> list[ShapedArray]:
if not isinstance(x, ShapedArray) or not isinstance(y, ShapedArray):
raise TypeError
if raise_to_shaped(x) != raise_to_shaped(y): raise TypeError
return [ShapedArray(x.shape, x.dtype)]
abstract_eval_rules[add_p] = binop_abstract_eval
abstract_eval_rules[mul_p] = binop_abstract_eval
def compare_abstract_eval(x: ShapedArray, y: ShapedArray) -> list[ShapedArray]:
if not isinstance(x, ShapedArray) or not isinstance(y, ShapedArray):
raise TypeError
if x.shape != y.shape: raise TypeError
return [ShapedArray(x.shape, np.dtype('bool'))]
abstract_eval_rules[greater_p] = compare_abstract_eval
abstract_eval_rules[less_p] = compare_abstract_eval
def vectorized_unop_abstract_eval(x: ShapedArray) -> list[ShapedArray]:
return [ShapedArray(x.shape, x.dtype)]
abstract_eval_rules[sin_p] = vectorized_unop_abstract_eval
abstract_eval_rules[cos_p] = vectorized_unop_abstract_eval
abstract_eval_rules[neg_p] = vectorized_unop_abstract_eval
def reduce_sum_abstract_eval(x: ShapedArray, *, axis: tuple[int, ...]
) -> list[ShapedArray]:
axis_ = set(axis)
new_shape = [d for i, d in enumerate(x.shape) if i not in axis_]
return [ShapedArray(tuple(new_shape), x.dtype)]
abstract_eval_rules[reduce_sum_p] = reduce_sum_abstract_eval
def broadcast_abstract_eval(x: ShapedArray, *, shape: Sequence[int],
axes: Sequence[int]) -> list[ShapedArray]:
return [ShapedArray(tuple(shape), x.dtype)]
abstract_eval_rules[broadcast_p] = broadcast_abstract_eval
要验证我们的 jaxprs 实现,我们可以添加一个make_jaxpr转换和一个漂亮的打印机:
from functools import lru_cache
@lru_cache() # ShapedArrays are hashable
def make_jaxpr_v1(f, *avals_in):
avals_in, in_tree = tree_flatten(avals_in)
f, out_tree = flatten_fun(f, in_tree)
builder = JaxprBuilder()
with new_main(JaxprTrace, builder) as main:
trace = JaxprTrace(main)
tracers_in = [trace.new_arg(aval) for aval in avals_in]
outs = f(*tracers_in)
tracers_out = [full_raise(trace, out) for out in outs]
jaxpr, consts = builder.build(tracers_in, tracers_out)
return jaxpr, consts, out_tree()
from collections import defaultdict
import string
class PPrint:
lines: list[tuple[int, str]]
def __init__(self, lines):
self.lines = lines
def indent(self, indent: int) -> 'PPrint':
return PPrint([(indent + orig_indent, s) for orig_indent, s in self.lines])
def __add__(self, rhs: 'PPrint') -> 'PPrint':
return PPrint(self.lines + rhs.lines)
def __rshift__(self, rhs: 'PPrint') -> 'PPrint':
if not rhs.lines: return self
if not self.lines: return rhs
indent, s = self.lines[-1]
indented_block = rhs.indent(indent + len(s))
common_line = s + ' ' * rhs.lines[0][0] + rhs.lines[0][1]
return PPrint(self.lines[:-1]
+ [(indent, common_line)]
+ indented_block.lines[1:])
def __str__(self) -> str:
return '\n'.join(' ' * indent + s for indent, s in self.lines)
def pp(s: Any) -> PPrint:
return PPrint([(0, line) for line in str(s).splitlines()])
def vcat(ps: list[PPrint]) -> PPrint:
return sum(ps, pp(''))
def pp_jaxpr(jaxpr: Jaxpr) -> PPrint:
namegen = (''.join(s) for r in it.count(1)
for s in it.permutations(string.ascii_lowercase, r))
names = defaultdict(lambda: next(namegen))
in_binders = ', '.join(var_str(names, x) for x in jaxpr.in_binders)
eqns = vcat([pp_eqn(names, e) for e in jaxpr.eqns])
outs = ', '.join(names[v] if isinstance(v, Var) else str(v.val)
for v in jaxpr.outs)
return (pp(f'{{ lambda {in_binders} .') +
((pp('let ') >> eqns) + pp(f'in ( {outs} ) }}')).indent(2))
def var_str(names: defaultdict[Var, str], v: Var) -> str:
return f'{names[v]}:{v.aval.str_short()}'
def pp_eqn(names: defaultdict[Var, str], eqn: JaxprEqn) -> PPrint:
rule = pp_rules.get(eqn.primitive)
if rule:
return rule(names, eqn)
else:
lhs = pp(' '.join(var_str(names, v) for v in eqn.out_binders))
rhs = (pp(eqn.primitive.name) >> pp_params(eqn.params) >>
pp(' '.join(names[x] if isinstance(x, Var) else str(x.val)
for x in eqn.inputs)))
return lhs >> pp(' = ') >> rhs
def pp_params(params: dict[str, Any]) -> PPrint:
items = sorted(params.items())
if items:
return pp(' [ ') >> vcat([pp(f'{k}={v}') for k, v in items]) >> pp(' ] ')
else:
return pp(' ')
Jaxpr.__repr__ = lambda self: str(pp_jaxpr(self))
pp_rules: dict[Primitive, Callable[..., PPrint]] = {}
```</details>
```py
jaxpr, consts, _ = make_jaxpr_v1(lambda x: 2. * x, raise_to_shaped(get_aval(3.)))
print(jaxpr)
print(typecheck_jaxpr(jaxpr))
{ lambda a:float64[] .
let b:float64[] = mul 2.0 a
in ( b ) }
(float64[]) -> (float64[])
但是这里有一个限制:由于find_top_trace是通过数据依赖操作的,make_jaxpr_v1无法将其给定的 Python 可调用对象执行的所有原始操作分阶段处理出来。例如:
jaxpr, consts, _ = make_jaxpr_v1(lambda: mul(2., 2.))
print(jaxpr)
{ lambda .
let
in ( 4.0 ) }
这正是omnistaging修复的问题。我们希望确保make_jaxpr启动的JaxprTrace始终被应用,而不管bind的任何输入是否被装箱在相应的JaxprTracer实例中。我们可以通过使用第一部分定义的dynamic_trace全局变量来实现这一点:
@contextmanager
def new_dynamic(main: MainTrace):
global dynamic_trace
prev_dynamic_trace, dynamic_trace = dynamic_trace, main
try:
yield
finally:
dynamic_trace = prev_dynamic_trace
@lru_cache()
def make_jaxpr(f: Callable, *avals_in: ShapedArray,
) -> tuple[Jaxpr, list[Any], PyTreeDef]:
avals_in, in_tree = tree_flatten(avals_in)
f, out_tree = flatten_fun(f, in_tree)
builder = JaxprBuilder()
with new_main(JaxprTrace, builder) as main:
with new_dynamic(main):
trace = JaxprTrace(main)
tracers_in = [trace.new_arg(aval) for aval in avals_in]
outs = f(*tracers_in)
tracers_out = [full_raise(trace, out) for out in outs]
jaxpr, consts = builder.build(tracers_in, tracers_out)
return jaxpr, consts, out_tree()
jaxpr, consts, _ = make_jaxpr(lambda: mul(2., 2.))
print(jaxpr)
{ lambda .
let a:float64[] = mul 2.0 2.0
in ( a ) }
以这种方式使用dynamic_trace在概念上与将当前解释器堆栈存储并使用JaxprTrace作为底部开始新的解释器堆栈是相同的。也就是说,比JaxprTrace.process_primitive低的堆栈解释器不会被应用(因为它不调用bind),尽管如果被跟踪到 jaxpr 的 Python 可调用对象本身使用转换,那么这些转换可以被推送到位于JaxprTrace上面的解释器堆栈中。但是临时存储解释器堆栈会破坏系统状态。dynamic_trace标记通过保持系统状态更简单来实现相同的目标。
这就是 jaxprs 的全部内容!有了 jaxprs,我们可以实现其余的主要 JAX 特性。
第三部分:jit,简化
虽然jit具有类似于转换的 API,因为它接受 Python 可调用对象作为参数,但在幕后它实际上是一个高阶原语,而不是转换。当参数化为函数时,一个原语是高阶的。
即时(“final style”)和分阶段(“initial style”)处理
处理高阶原语有两个选择。每种选择都需要不同的跟踪方法,并产生不同的权衡:
-
即时处理,在
bind将 Python 可调用对象作为参数。 我们推迟形成 jaxpr,直到可能的最后一刻,即在解释器栈底部运行最终解释器时。这样我们可以在解释器栈底部换上一个JaxprTrace,从而分阶段而不是执行所有原始操作。采用这种方法,堆栈中的转换会在我们像往常一样执行 Python 可调用对象时应用。这种方法实现起来可能非常棘手,但尽可能通用,因为它允许高阶原语不提升其参数的抽象级别,从而允许数据相关的 Python 控制流。我们称之为使用“最终风格高阶原语”,采用了迄今为止使用的“追踪时排除”最终风格变换。 -
分阶段处理,在
bind将 jaxpr 作为参数。 在我们调用bind之前,在原始包装器中我们可以直接使用make_jaxpr来预先形成 jaxpr 并完全结束 Python 可调用对象。在这种情况下,make_jaxpr将其JaxprTrace放在解释器栈的顶部,并且没有低于堆栈的变换会通过闭合的 Tracer 输入到我们追踪的 Python 可调用对象中。 (在 Python 可调用对象内部应用的转换会像往常一样应用,被添加到 JaxprTrace 之上的堆栈中。)相反,堆栈中较低的转换稍后将应用于调用原始操作,并且调用原始操作的规则必须然后转换 jaxpr 本身。由于我们预先追踪到一个 jaxpr,这种方法不能支持数据相关的 Python 控制流,但它实现起来更为直接。我们将这种类型的高阶原语称为“初始风格高阶原语”,并说其 jaxpr 处理转换规则是“初始风格变换规则”。
后一种方法适用于jit,因为我们不需要支持用户提供的 Python 可调用对象中的数据相关 Python 控制流,因为jit的整个目的是将计算从 Python 阶段出来以供 XLA 执行。(相反,custom_jvp是一个高阶原语,我们希望在其中支持数据相关的 Python 控制流。)
在阅读了类型标签最终解释器论文后,我们从历史上开始使用“初始风格”和“最终风格”术语,并开玩笑称 JAX 是“未类型化的标签满足最终解释器”的实现。我们并不声称传承(或理解)这些术语背后的任何深层含义;我们宽泛地使用“初始风格”来表示“构建 AST 然后转换它”,并且我们使用“最终风格”来表示“追踪时转换”。但这只是不精确但易记的行话。
使用初始风格方法,这里是用户界面的jit包装器:
def jit(f):
def f_jitted(*args):
avals_in = [raise_to_shaped(get_aval(x)) for x in args]
jaxpr, consts, out_tree = make_jaxpr(f, *avals_in)
outs = bind(xla_call_p, *consts, *args, jaxpr=jaxpr, num_consts=len(consts))
return tree_unflatten(out_tree, outs)
return f_jitted
xla_call_p = Primitive('xla_call')
对于任何新的原语,我们都需要为其提供转换规则,从其评估规则开始。当我们评估xla_call原语的应用时,我们希望将计算分阶段到 XLA。这涉及将 jaxpr 转换为 XLA HLO 程序,将参数值传输到 XLA 设备,执行 XLA 程序,并将结果传输回来。我们将缓存 XLA HLO 编译,以便于每个jit函数只需在参数形状和 dtype 签名上执行一次。
首先,一些实用工具。
class IDHashable:
val: Any
def __init__(self, val):
self.val = val
def __hash__(self) -> int:
return id(self.val)
def __eq__(self, other):
return type(other) is IDHashable and id(self.val) == id(other.val)
接下来,我们将为xla_call定义评估规则:
from jax._src import xla_bridge as xb
from jax._src.lib import xla_client as xc
xe = xc._xla
xops = xc._xla.ops
def xla_call_impl(*args, jaxpr: Jaxpr, num_consts: int):
consts, args = args[:num_consts], args[num_consts:]
hashable_consts = tuple(map(IDHashable, consts))
execute = xla_callable(IDHashable(jaxpr), hashable_consts)
return execute(*args)
impl_rules[xla_call_p] = xla_call_impl
@lru_cache()
def xla_callable(hashable_jaxpr: IDHashable,
hashable_consts: tuple[IDHashable, ...]):
jaxpr: Jaxpr = hashable_jaxpr.val
typecheck_jaxpr(jaxpr)
consts = [x.val for x in hashable_consts]
in_avals = [v.aval for v in jaxpr.in_binders[len(consts):]]
c = xc.XlaBuilder('xla_call')
xla_consts = _xla_consts(c, consts)
xla_params = _xla_params(c, in_avals)
outs = jaxpr_subcomp(c, jaxpr, xla_consts + xla_params)
out = xops.Tuple(c, outs)
compiled = xb.get_backend(None).compile(
xc._xla.mlir.xla_computation_to_mlir_module(c.build(out)))
return partial(execute_compiled, compiled, [v.aval for v in jaxpr.outs])
def _xla_consts(c: xe.XlaBuilder, consts: list[Any]) -> list[xe.XlaOp]:
unique_consts = {id(cnst): cnst for cnst in consts}
xla_consts = {
id_: xops.ConstantLiteral(c, cnst) for id_, cnst in unique_consts.items()}
return [xla_consts[id(cnst)] for cnst in consts]
def _xla_params(c: xe.XlaBuilder, avals_in: list[ShapedArray]) -> list[xe.XlaOp]:
return [xops.Parameter(c, i, _xla_shape(a)) for i, a in enumerate(avals_in)]
def _xla_shape(aval: ShapedArray) -> xe.Shape:
return xc.Shape.array_shape(xc.dtype_to_etype(aval.dtype), aval.shape)
主要操作在xla_callable中进行,它使用jaxpr_subcomp将 jaxpr 编译成 XLA HLO 程序,然后返回一个可调用对象来执行编译后的程序:
def jaxpr_subcomp(c: xe.XlaBuilder, jaxpr: Jaxpr, args: list[xe.XlaOp]
) -> list[xe.XlaOp]:
env: dict[Var, xe.XlaOp] = {}
def read(x: Atom) -> xe.XlaOp:
return env[x] if type(x) is Var else xops.Constant(c, np.asarray(x.val))
def write(v: Var, val: xe.XlaOp) -> None:
env[v] = val
map(write, jaxpr.in_binders, args)
for eqn in jaxpr.eqns:
in_avals = [x.aval for x in eqn.inputs]
in_vals = map(read, eqn.inputs)
rule = xla_translations[eqn.primitive]
out_vals = rule(c, in_avals, in_vals, **eqn.params)
map(write, eqn.out_binders, out_vals)
return map(read, jaxpr.outs)
def execute_compiled(compiled, out_avals, *args):
input_bufs = input_handlers[type(x) for x in args]
out_bufs = compiled.execute(input_bufs)
return [handle_result(aval, buf) for aval, buf in zip(out_avals, out_bufs)]
default_input_handler = xb.get_backend(None).buffer_from_pyval
input_handlers = {ty: default_input_handler for ty in
[bool, int, float, np.ndarray, np.float64, np.float32]}
def handle_result(aval: ShapedArray, buf):
del aval # Unused for now
return np.asarray(buf)
xla_translations = {}
请注意,jaxpr_subcomp具有简单解释器的结构。这是一个常见模式:我们处理 jaxprs 的方式通常是使用解释器。与任何解释器一样,我们需要为每个原语定义一个解释规则:
def direct_translation(op, c, in_avals, in_vals):
del c, in_avals
return [op(*in_vals)]
xla_translations[add_p] = partial(direct_translation, xops.Add)
xla_translations[mul_p] = partial(direct_translation, xops.Mul)
xla_translations[neg_p] = partial(direct_translation, xops.Neg)
xla_translations[sin_p] = partial(direct_translation, xops.Sin)
xla_translations[cos_p] = partial(direct_translation, xops.Cos)
xla_translations[greater_p] = partial(direct_translation, xops.Gt)
xla_translations[less_p] = partial(direct_translation, xops.Lt)
def reduce_sum_translation(c, in_avals, in_vals, *, axis):
(x_aval,), (x,) = in_avals, in_vals
zero = xops.ConstantLiteral(c, np.array(0, x_aval.dtype))
subc = xc.XlaBuilder('add')
shape = _xla_shape(ShapedArray((), x_aval.dtype))
xops.Add(xops.Parameter(subc, 0, shape), xops.Parameter(subc, 1, shape))
return [xops.Reduce(c, [x], [zero], subc.build(), axis)]
xla_translations[reduce_sum_p] = reduce_sum_translation
def broadcast_translation(c, in_avals, in_vals, *, shape, axes):
x, = in_vals
dims_complement = [i for i in range(len(shape)) if i not in axes]
return [xops.BroadcastInDim(x, shape, dims_complement)]
xla_translations[broadcast_p] = broadcast_translation
有了这个,我们现在可以使用jit来分阶段、编译和执行 XLA 程序了!
@jit
def f(x, y):
print('tracing!')
return sin(x) * cos(y)
z = f(3., 4.) # 'tracing!' prints the first time
print(z)
tracing!
-0.09224219304455371
z = f(4., 5.) # 'tracing!' doesn't print, compilation cache hit!
print(z)
-0.21467624978306993
@jit
def f(x):
return reduce_sum(x, axis=0)
print(f(np.array([1., 2., 3.])))
6.0
def f(x):
y = sin(x) * 2.
z = - y + x
return z
def deriv(f):
return lambda x: jvp(f, (x,), (1.,))[1]
print( deriv(deriv(f))(3.))
print(jit(deriv(deriv(f)))(3.))
0.2822400161197344
0.2822400161197344
而不是实现jit以首先对 jaxpr 进行跟踪,然后将 jaxpr 降低到 XLA HLO,我们可能看起来可以跳过 jaxpr 步骤,而在跟踪时直接降低到 HLO。也就是说,也许我们可以用一个Trace和Tracer实现jit,在每个原语绑定时逐步追加到 XLA HLO 图中。目前这样做是正确的,但当我们引入编译的 SPMD 计算时,就不可能了,因为在编译程序之前我们必须知道所需的副本数量。
我们尚未为xla_call_p定义任何转换规则,除了其评估规则。也就是说,我们尚不能做vmap-of-jit或jvp-of-jit甚至jit-of-jit。相反,jit必须处于“顶层”。让我们来修复这个问题!
def xla_call_jvp_rule(primals, tangents, *, jaxpr, num_consts):
del num_consts # Unused
new_jaxpr, new_consts = jvp_jaxpr(jaxpr)
outs = bind(xla_call_p, *new_consts, *primals, *tangents, jaxpr=new_jaxpr,
num_consts=len(new_consts))
n = len(outs) // 2
primals_out, tangents_out = outs[:n], outs[n:]
return primals_out, tangents_out
jvp_rules[xla_call_p] = xla_call_jvp_rule
@lru_cache()
def jvp_jaxpr(jaxpr: Jaxpr) -> tuple[Jaxpr, list[Any]]:
def jvp_traceable(*primals_and_tangents):
n = len(primals_and_tangents) // 2
primals, tangents = primals_and_tangents[:n], primals_and_tangents[n:]
return jvp(jaxpr_as_fun(jaxpr), primals, tangents)
in_avals = [v.aval for v in jaxpr.in_binders]
new_jaxpr, new_consts, _ = make_jaxpr(jvp_traceable, *in_avals, *in_avals)
return new_jaxpr, new_consts
def xla_call_vmap_rule(axis_size, vals_in, dims_in, *, jaxpr, num_consts):
del num_consts # Unused
new_jaxpr, new_consts = vmap_jaxpr(jaxpr, axis_size, tuple(dims_in))
outs = bind(xla_call_p, *new_consts, *vals_in, jaxpr=new_jaxpr,
num_consts=len(new_consts))
return outs, [0] * len(outs)
vmap_rules[xla_call_p] = xla_call_vmap_rule
@lru_cache()
def vmap_jaxpr(jaxpr: Jaxpr, axis_size: int, bdims_in: tuple[BatchAxis, ...]
) -> tuple[Jaxpr, list[Any]]:
vmap_traceable = vmap(jaxpr_as_fun(jaxpr), tuple(bdims_in))
in_avals = [unmapped_aval(axis_size, d, v.aval)
for v, d in zip(jaxpr.in_binders, bdims_in)]
new_jaxpr, new_consts, _ = make_jaxpr(vmap_traceable, *in_avals)
return new_jaxpr, new_consts
def unmapped_aval(axis_size: int, batch_dim: BatchAxis, aval: ShapedArray
) -> ShapedArray:
if batch_dim is not_mapped:
return aval
else:
shape = list(aval.shape)
shape.insert(batch_dim, axis_size)
return ShapedArray(tuple(shape), aval.dtype)
def xla_call_abstract_eval_rule(*in_types, jaxpr, num_consts):
del num_consts # Unused
jaxpr_type = typecheck_jaxpr(jaxpr)
if not all(t1 == t2 for t1, t2 in zip(jaxpr_type.in_types, in_types)):
raise TypeError
return jaxpr_type.out_types
abstract_eval_rules[xla_call_p] = xla_call_abstract_eval_rule
def xla_call_translation(c, in_avals, in_vals, *, jaxpr, num_consts):
del num_consts # Only used at top-level.
# Calling jaxpr_subcomp directly would inline. We generate a Call HLO instead.
subc = xc.XlaBuilder('inner xla_call')
xla_params = _xla_params(subc, in_avals)
outs = jaxpr_subcomp(subc, jaxpr, xla_params)
subc = subc.build(xops.Tuple(subc, outs))
return destructure_tuple(c, xops.Call(c, subc, in_vals))
xla_translations[xla_call_p] = xla_call_translation
def destructure_tuple(c, tup):
num_elements = len(c.get_shape(tup).tuple_shapes())
return [xops.GetTupleElement(tup, i) for i in range(num_elements)]
@jit
def f(x):
print('tracing!')
y = sin(x) * 2.
z = - y + x
return z
x, xdot = 3., 1.
y, ydot = jvp(f, (x,), (xdot,))
print(y)
print(ydot)
tracing!
2.7177599838802657
2.979984993200891
y, ydot = jvp(f, (x,), (xdot,)) # 'tracing!' not printed
ys = vmap(f, (0,))(np.arange(3.))
print(ys)
[ 0\. -0.68294197 0.18140515]
一个遗漏的部分是数组的设备内存持久性。也就是说,我们已经定义了handle_result以将结果作为 NumPy 数组传输回 CPU 内存,但通常最好避免仅为了下一步操作而传输结果。我们可以通过引入Array类来实现这一点,它可以包装 XLA 缓冲区,同时鸭子类型numpy.ndarray:
def handle_result(aval: ShapedArray, buf): # noqa: F811
return Array(aval, buf)
class Array:
buf: Any
aval: ShapedArray
def __init__(self, aval, buf):
self.aval = aval
self.buf = buf
dtype = property(lambda self: self.aval.dtype)
shape = property(lambda self: self.aval.shape)
ndim = property(lambda self: self.aval.ndim)
def __array__(self): return np.asarray(self.buf)
def __repr__(self): return repr(np.asarray(self.buf))
def __str__(self): return str(np.asarray(self.buf))
_neg = staticmethod(neg)
_add = staticmethod(add)
_radd = staticmethod(add)
_mul = staticmethod(mul)
_rmul = staticmethod(mul)
_gt = staticmethod(greater)
_lt = staticmethod(less)
input_handlers[Array] = lambda x: x.buf
jax_types.add(Array)
@jit
def f(x):
y = sin(x) * 2.
z = - y + x
return z
x, xdot = 3., 1.
y, ydot = jvp(f, (x,), (xdot,))
print(y)
print(ydot)
2.7177599838802657
2.979984993200891
def pprint_xla_call(names: defaultdict[Var, str], eqn: JaxprEqn) -> PPrint:
lhs = pp(' '.join(var_str(names, v) for v in eqn.out_binders))
params_without_jaxpr = {k:v for k, v in eqn.params.items() if k != 'jaxpr'}
rhs = (pp(eqn.primitive.name) >> pp_params(params_without_jaxpr) >>
pp(' '.join(names[x] if isinstance(x, Var) else str(x.val)
for x in eqn.inputs)))
return vcat([lhs >> pp(' = ') >> rhs,
pp_jaxpr(eqn.params['jaxpr']).indent(2)])
pp_rules[xla_call_p] = pprint_xla_call
```</details>
## 第四部分:`linearize`和`vjp`(以及`grad`!)
`linearize`和`vjp`的自动微分函数都建立在`jvp`之上,但也涉及 jaxprs。这是因为两者都涉及分阶段或延迟计算。
### `linearize`
对于`linearize`的情况,我们想要分离出`jvp`计算的线性部分。也就是说,用[Haskell 类型签名](https://wiki.haskell.org/Type_signature)来说,如果我们有`jvp : (a -> b) -> (a, T a) -> (b, T b)`,那么我们会写成`linearize : (a -> b) -> a -> (b, T a -o T b)`,使用`T a`表示“`a`的切线类型”,并使用“棒棒糖”`-o`而不是箭头`->`来指示一个*线性*函数。我们也是以`jvp`的语义来定义`linearize`:
```py
y, f_lin = linearize(f, x)
y_dot = f_lin(x_dot)
对于(y, y_dot),与原先相同的结果如下:
y, y_dot = jvp(f, (x,), (x_dot,))
在应用f_lin时,不会重新执行任何线性化工作。我们将延迟的线性部分f_lin : T a -o T b表示为一个 jaxpr。
顺便说一句,既然我们有了线性箭头-o,我们可以为jvp提供一个稍微更详细的类型:
jvp : (a -> b) -> (UnrestrictedUse a, T a) -o (UnrestrictedUse b, T b)
我们在这里编写UnrestrictedUse只是为了表明我们有一个特殊的对,第一个元素可以以非线性的方式使用。与线性箭头结合使用时,此符号只是用来表示函数jvp f以非线性方式使用其第一个输入,但以线性方式使用其第二个输入,生成相应的非线性输出(可以以非线性方式使用),与线性输出配对。这种更精细的类型签名编码了jvp f中的数据依赖关系,对于部分评估非常有用。
要从 JVP 构建f_lin的 jaxpr,我们需要执行部分评估:在我们追踪时评估所有原始值,但是将切线计算分阶段到一个 jaxpr 中。这是我们构建 jaxprs 的第二种方式。但是,与make_jaxpr及其基础的JaxprTrace/JaxprTracer解释器的目标是分阶段所有原始绑定不同,这第二种方法仅分阶段那些具有对切线输入的数据依赖性的原始绑定。
首先,一些实用工具:
def split_half(lst: list[Any]) -> tuple[list[Any], list[Any]]:
assert not len(lst) % 2
return split_list(lst, len(lst) // 2)
def merge_lists(which: list[bool], l1: list[Any], l2: list[Any]) -> list[Any]:
l1, l2 = iter(l1), iter(l2)
out = [next(l2) if b else next(l1) for b in which]
assert next(l1, None) is next(l2, None) is None
return out
接下来,我们将编写linearize,通过将jvp与一般的部分评估转换组合在一起:
def linearize_flat(f, *primals_in):
pvals_in = ([PartialVal.known(x) for x in primals_in] +
[PartialVal.unknown(vspace(get_aval(x))) for x in primals_in])
def f_jvp(*primals_tangents_in):
primals_out, tangents_out = jvp(f, *split_half(primals_tangents_in))
return [*primals_out, *tangents_out]
jaxpr, pvals_out, consts = partial_eval_flat(f_jvp, pvals_in)
primal_pvals, _ = split_half(pvals_out)
assert all(pval.is_known for pval in primal_pvals)
primals_out = [pval.const for pval in primal_pvals]
f_lin = lambda *tangents: eval_jaxpr(jaxpr, [*consts, *tangents])
return primals_out, f_lin
def linearize(f, *primals_in):
primals_in_flat, in_tree = tree_flatten(primals_in)
f, out_tree = flatten_fun(f, in_tree)
primals_out_flat, f_lin_flat = linearize_flat(f, *primals_in_flat)
primals_out = tree_unflatten(out_tree(), primals_out_flat)
def f_lin(*tangents_in):
tangents_in_flat, in_tree2 = tree_flatten(tangents_in)
if in_tree != in_tree2: raise TypeError
tangents_out_flat = f_lin_flat(*tangents_in_flat)
return tree_unflatten(out_tree(), tangents_out_flat)
return primals_out, f_lin
def vspace(aval: ShapedArray) -> ShapedArray:
return raise_to_shaped(aval) # TODO handle integers?
现在我们转向一般的部分评估转换。目标是接受一个 Python 可调用函数和一个输入列表,其中一些已知,一些未知,并产生(1)可以从已知输入计算出来的所有输出,以及(2)表示仅在其余输入已知后才能执行的 Python 可调用函数计算的 japxr。
这种转换很难用一个类型签名来总结。如果我们假设输入函数的类型签名是(a1, a2) -> (b1, b2),其中a1和a2分别表示已知和未知的输入,并且其中b1仅对a1有数据依赖性,而b2对a2有一些数据依赖性,那么我们可能会写成:
partial_eval : ((a1, a2) -> (b1, b2)) -> a1 -> exists r. (b1, r, (r, a2) -> b2)
简言之,给定类型为 a1 的输入值,partial_eval 将生成类型为 b1 的输出值以及代表在第二阶段完成计算所需的存在量化类型 r 的“残余”值。它还会生成一个类型为 (r, a2) -> b2 的函数,该函数接受残余值以及剩余输入,并生成剩余输出。
我们喜欢将部分评估视为将一个计算“解压”为两个的过程。例如,考虑以下 jaxpr:
{ lambda a:float64[] .
let b:float64[] = sin a
c:float64[] = neg b
in ( c ) }
JVP 的 jaxpr 将如下所示:
{ lambda a:float64[] b:float64[] .
let c:float64[] = sin a
d:float64[] = cos a
e:float64[] = mul d b
f:float64[] = neg c
g:float64[] = neg e
in ( f, g ) }
如果我们想象将部分评估应用于此 jaxpr,第一个输入已知,第二个输入未知,我们将 JVP 的 jaxpr “解压”为原始和切线 jaxpr:
{ lambda a:float64[] .
let c:float64[] = sin a
d:float64[] = cos a
f:float64[] = neg c
in ( f, d ) }
{ lambda d:float64[] b:float64[] .
let e:float64[] = mul d b
g:float64[] = neg e
in ( g ) }
这第二个 jaxpr 表示我们从 linearize 中希望得到的线性计算。
然而,与此 jaxpr 示例不同的是,我们希望在评估输入的 Python 可调用函数时,对已知值进行计算。换句话说,我们不想在整个函数 (a1, a2) -> (b1, b2) 的 jaxpr 中首先将所有操作分离出 Python,然后再确定哪些可以立即评估,哪些必须延迟。我们只想形成那些由于依赖于未知输入而必须延迟的操作的 jaxpr。在自动微分的背景下,这正是使我们能够处理诸如 grad(lambda x: x**2 if x > 0 else 0.) 函数的特性。Python 控制流能够正常工作,因为部分评估保持了 Python 中的原始计算。因此,我们的 Trace 和 Tracer 子类必须动态地分辨出哪些可以评估,哪些必须分离到 jaxpr 中。
首先,我们从 PartialVal 类开始,它表示可以是已知或未知的值:
class PartialVal(NamedTuple):
aval: ShapedArray
const: Optional[Any]
@classmethod
def known(cls, val: Any):
return PartialVal(get_aval(val), val)
@classmethod
def unknown(cls, aval: ShapedArray):
return PartialVal(aval, None)
is_known = property(lambda self: self.const is not None)
is_unknown = property(lambda self: self.const is None)
部分评估将接受一个表示输入的 PartialVal 列表,并返回一个表示延迟计算的 jaxpr 的 PartialVal 输出列表:
def partial_eval_flat(f: Callable, pvals_in: list[PartialVal]
) -> tuple[Jaxpr, list[PartialVal], list[Any]]:
with new_main(PartialEvalTrace) as main:
trace = PartialEvalTrace(main)
tracers_in = [trace.new_arg(pval) for pval in pvals_in]
outs = f(*tracers_in)
tracers_out = [full_raise(trace, out) for out in outs]
pvals_out = [t.pval for t in tracers_out]
unk_tracers_in = [t for t in tracers_in if t.pval.is_unknown]
unk_tracers_out = [t for t in tracers_out if t.pval.is_unknown]
jaxpr, consts = tracers_to_jaxpr(unk_tracers_in, unk_tracers_out)
return jaxpr, pvals_out, consts
接下来,我们需要实现 PartialEvalTrace 及其 PartialEvalTracer。此解释器将在跟踪数据依赖关系的同时动态构建 jaxpr。为此,它在 PartialEvalTracer 节点(代表分阶段的值)和 JaxprRecipe 节点(代表如何从其他值计算某些值的公式)之间建立了一个二部有向无环图(DAG)。一种类型的配方是 JaxprEqnRecipe,对应于 JaxprEqn 的原语应用,但我们还有常量和 Lambda 绑定器的配方类型:
from weakref import ref, ReferenceType
class LambdaBindingRecipe(NamedTuple):
pass
class ConstRecipe(NamedTuple):
val: Any
class JaxprEqnRecipe(NamedTuple):
prim: Primitive
tracers_in: list['PartialEvalTracer']
params: dict[str, Any]
avals_out: list[ShapedArray]
tracer_refs_out: list['ReferenceType[PartialEvalTracer]']
JaxprRecipe = Union[LambdaBindingRecipe, ConstRecipe, JaxprEqnRecipe]
class PartialEvalTracer(Tracer):
pval: PartialVal
recipe: Optional[JaxprRecipe]
def __init__(self, trace, pval, recipe):
self._trace = trace
self.pval = pval
self.recipe = recipe
aval = property(lambda self: self.pval.aval)
def full_lower(self):
if self.pval.is_known:
return full_lower(self.pval.const)
return self
PartialEvalTrace 包含构建 JaxprRecipe 和 PartialEvalTracer 图形的逻辑。每个参数对应于 LambdaBindingRecipe 叶节点,每个常量都是一个 ConstRecipe 叶节点,保存对常量的引用。所有其他跟踪器和配方都来自 process_primitive,它使用 JaxprEqnRecipe 形成具有 JaxprEqn 的原语应用的跟踪器。
对于大多数原语,process_primitive逻辑很简单:如果所有输入都已知,我们可以在已知值上绑定原语(在 Python 中评估它),并避免形成对应于输出的追踪器。如果任何输入未知,则我们转而进行JaxprEqnRecipe的阶段输出,表示原语应用。为了构建代表未知输出的追踪器,我们需要 aval,这些 aval 来自抽象评估规则。(请注意,追踪器引用JaxprEqnRecipe,而JaxprEqnRecipe引用追踪器;我们通过使用弱引用来避免循环垃圾。)
process_primitive逻辑适用于大多数原语,但xla_call_p需要递归处理。因此,我们在partial_eval_rules字典中特别处理它的规则。
class PartialEvalTrace(Trace):
def new_arg(self, pval: PartialVal) -> Any:
return PartialEvalTracer(self, pval, LambdaBindingRecipe())
def lift(self, val: Any) -> PartialEvalTracer:
return PartialEvalTracer(self, PartialVal.known(val), None)
pure = lift
def instantiate_const(self, tracer: PartialEvalTracer) -> PartialEvalTracer:
if tracer.pval.is_unknown:
return tracer
else:
pval = PartialVal.unknown(raise_to_shaped(tracer.aval))
return PartialEvalTracer(self, pval, ConstRecipe(tracer.pval.const))
def process_primitive(self, primitive, tracers, params):
if all(t.pval.is_known for t in tracers):
return bind(primitive, *map(full_lower, tracers), **params)
rule = partial_eval_rules.get(primitive)
if rule: return rule(self, tracers, **params)
tracers_in = [self.instantiate_const(t) for t in tracers]
avals_in = [t.aval for t in tracers_in]
avals_out = abstract_eval_rulesprimitive
tracers_out = [PartialEvalTracer(self, PartialVal.unknown(aval), None)
for aval in avals_out]
eqn = JaxprEqnRecipe(primitive, tracers_in, params, avals_out,
map(ref, tracers_out))
for t in tracers_out: t.recipe = eqn
return tracers_out
partial_eval_rules = {}
现在我们可以用PartialEvalTrace构建 jaxprs 的图形表示,我们需要一种机制将图形表示转换为标准的 jaxpr。jaxpr 对应于图形的拓扑排序。
def tracers_to_jaxpr(tracers_in: list[PartialEvalTracer],
tracers_out: list[PartialEvalTracer]):
tracer_to_var: dict[int, Var] = {id(t): Var(raise_to_shaped(t.aval))
for t in tracers_in}
constvar_to_val: dict[int, Any] = {}
constid_to_var: dict[int, Var] = {}
processed_eqns: set[int] = set()
eqns: list[JaxprEqn] = []
for t in toposort(tracers_out, tracer_parents):
if isinstance(t.recipe, LambdaBindingRecipe):
assert id(t) in set(map(id, tracers_in))
elif isinstance(t.recipe, ConstRecipe):
val = t.recipe.val
var = constid_to_var.get(id(val))
if var is None:
aval = raise_to_shaped(get_aval(val))
var = constid_to_var[id(val)] = Var(aval)
constvar_to_val[var] = val
tracer_to_var[id(t)] = var
elif isinstance(t.recipe, JaxprEqnRecipe):
if id(t.recipe) not in processed_eqns:
eqns.append(recipe_to_eqn(tracer_to_var, t.recipe))
processed_eqns.add(id(t.recipe))
else:
raise TypeError(t.recipe)
constvars, constvals = unzip2(constvar_to_val.items())
in_binders = constvars + [tracer_to_var[id(t)] for t in tracers_in]
out_vars = [tracer_to_var[id(t)] for t in tracers_out]
jaxpr = Jaxpr(in_binders, eqns, out_vars)
typecheck_jaxpr(jaxpr)
return jaxpr, constvals
def recipe_to_eqn(tracer_to_var: dict[int, Var], recipe: JaxprEqnRecipe
) -> JaxprEqn:
inputs = [tracer_to_var[id(t)] for t in recipe.tracers_in]
out_binders = [Var(aval) for aval in recipe.avals_out]
for t_ref, var in zip(recipe.tracer_refs_out, out_binders):
if t_ref() is not None: tracer_to_var[id(t_ref())] = var
return JaxprEqn(recipe.prim, inputs, recipe.params, out_binders)
def tracer_parents(t: PartialEvalTracer) -> list[PartialEvalTracer]:
return t.recipe.tracers_in if isinstance(t.recipe, JaxprEqnRecipe) else []
def toposort(out_nodes: list[Any], parents: Callable[[Any], list[Any]]):
if not out_nodes: return []
out_nodes = remove_duplicates(out_nodes)
child_counts = {}
stack = list(out_nodes)
while stack:
node = stack.pop()
if id(node) in child_counts:
child_counts[id(node)] += 1
else:
child_counts[id(node)] = 1
stack.extend(parents(node))
for node in out_nodes:
child_counts[id(node)] -= 1
sorted_nodes = []
childless_nodes = [node for node in out_nodes if not child_counts[id(node)]]
while childless_nodes:
node = childless_nodes.pop()
sorted_nodes.append(node)
for parent in parents(node):
if child_counts[id(parent)] == 1:
childless_nodes.append(parent)
else:
child_counts[id(parent)] -= 1
sorted_nodes = sorted_nodes[::-1]
check_toposort(sorted_nodes, parents)
return sorted_nodes
def remove_duplicates(lst):
seen = set()
return [x for x in lst if id(x) not in seen and not seen.add(id(x))]
def check_toposort(nodes: list[Any], parents: Callable[[Any], list[Any]]):
seen = set()
for node in nodes:
assert all(id(parent) in seen for parent in parents(node))
seen.add(id(node))
```</details>
现在我们可以进行线性化了!
```py
y, sin_lin = linearize(sin, 3.)
print(y, sin(3.))
print(sin_lin(1.), cos(3.))
0.1411200080598672 0.1411200080598672
-0.9899924966004454 -0.9899924966004454
要处理linearize-of-jit,我们仍然需要为xla_call_p编写部分评估规则。除了追踪器的记账外,主要任务是对 jaxpr 执行部分评估,将其“解压”为两个 jaxpr。
实际上有两个规则需要编写:一个是跟踪时间部分评估的规则,我们将其称为xla_call_partial_eval,另一个是 jaxprs 的部分评估规则,我们将其称为xla_call_peval_eqn。
def xla_call_partial_eval(trace, tracers, *, jaxpr, num_consts):
del num_consts # Unused
in_unknowns = [not t.pval.is_known for t in tracers]
jaxpr1, jaxpr2, out_unknowns, num_res = partial_eval_jaxpr(jaxpr, in_unknowns)
known_tracers, unknown_tracers = partition_list(in_unknowns, tracers)
known_vals = [t.pval.const for t in known_tracers]
outs1_res = bind(xla_call_p, *known_vals, jaxpr=jaxpr1, num_consts=0)
outs1, res = split_list(outs1_res, len(jaxpr1.outs) - num_res)
res_tracers = [trace.instantiate_const(full_raise(trace, x)) for x in res]
outs2 = [PartialEvalTracer(trace, PartialVal.unknown(v.aval), None)
for v in jaxpr2.outs]
eqn = JaxprEqnRecipe(xla_call_p, res_tracers + unknown_tracers,
dict(jaxpr=jaxpr2, num_consts=0),
[v.aval for v in jaxpr2.outs], map(ref, outs2))
for t in outs2: t.recipe = eqn
return merge_lists(out_unknowns, outs1, outs2)
partial_eval_rules[xla_call_p] = xla_call_partial_eval
def partial_eval_jaxpr(jaxpr: Jaxpr, in_unknowns: list[bool],
instantiate: Optional[list[bool]] = None,
) -> tuple[Jaxpr, Jaxpr, list[bool], int]:
env: dict[Var, bool] = {}
residuals: set[Var] = set()
def read(x: Atom) -> bool:
return type(x) is Var and env[x]
def write(unk: bool, v: Var) -> None:
env[v] = unk
def new_res(x: Atom) -> Atom:
if type(x) is Var: residuals.add(x)
return x
eqns1, eqns2 = [], []
map(write, in_unknowns, jaxpr.in_binders)
for eqn in jaxpr.eqns:
unks_in = map(read, eqn.inputs)
rule = partial_eval_jaxpr_rules.get(eqn.primitive)
if rule:
eqn1, eqn2, unks_out, res = rule(unks_in, eqn)
eqns1.append(eqn1); eqns2.append(eqn2); residuals.update(res)
map(write, unks_out, eqn.out_binders)
elif any(unks_in):
inputs = [v if unk else new_res(v) for unk, v in zip(unks_in, eqn.inputs)]
eqns2.append(JaxprEqn(eqn.primitive, inputs, eqn.params, eqn.out_binders))
map(partial(write, True), eqn.out_binders)
else:
eqns1.append(eqn)
map(partial(write, False), eqn.out_binders)
out_unknowns = map(read, jaxpr.outs)
if instantiate is not None:
for v, uk, inst in zip(jaxpr.outs, out_unknowns, instantiate):
if inst and not uk: new_res(v)
out_unknowns = map(op.or_, out_unknowns, instantiate)
residuals, num_res = list(residuals), len(residuals)
assert all(type(v) is Var for v in residuals), residuals
ins1, ins2 = partition_list(in_unknowns, jaxpr.in_binders)
outs1, outs2 = partition_list(out_unknowns, jaxpr.outs)
jaxpr1 = Jaxpr(ins1, eqns1, outs1 + residuals)
jaxpr2 = Jaxpr(residuals + ins2, eqns2, outs2)
typecheck_partial_eval_jaxpr(jaxpr, in_unknowns, out_unknowns, jaxpr1, jaxpr2)
return jaxpr1, jaxpr2, out_unknowns, num_res
def typecheck_partial_eval_jaxpr(jaxpr, unks_in, unks_out, jaxpr1, jaxpr2):
jaxprty = typecheck_jaxpr(jaxpr) # (a1, a2) -> (b1, b2 )
jaxpr1ty = typecheck_jaxpr(jaxpr1) # a1 -> (b1, res)
jaxpr2ty = typecheck_jaxpr(jaxpr2) # (res, a2) -> b2
a1, a2 = partition_list(unks_in, jaxprty.in_types)
b1, b2 = partition_list(unks_out, jaxprty.out_types)
b1_, res = split_list(jaxpr1ty.out_types, len(b1))
res_, a2_ = split_list(jaxpr2ty.in_types, len(res))
b2_ = jaxpr2ty.out_types
if jaxpr1ty.in_types != a1: raise TypeError
if jaxpr2ty.out_types != b2: raise TypeError
if b1 != b1_: raise TypeError
if res != res_: raise TypeError
if a2 != a2_: raise TypeError
if b2 != b2_: raise TypeError
partial_eval_jaxpr_rules = {}
def xla_call_peval_eqn(unks_in: list[bool], eqn: JaxprEqn,
) -> tuple[JaxprEqn, JaxprEqn, list[bool], list[Var]]:
jaxpr = eqn.params['jaxpr']
jaxpr1, jaxpr2, unks_out, num_res = partial_eval_jaxpr(jaxpr, unks_in)
ins1, ins2 = partition_list(unks_in, eqn.inputs)
out_binders1, out_binders2 = partition_list(unks_out, eqn.out_binders)
residuals = [Var(v.aval) for v in jaxpr2.in_binders[:num_res]]
eqn1 = JaxprEqn(xla_call_p, ins1, dict(jaxpr=jaxpr1, num_consts=0),
out_binders1 + residuals)
eqn2 = JaxprEqn(xla_call_p, residuals + ins2,
dict(jaxpr=jaxpr2, num_consts=0), out_binders2)
return eqn1, eqn2, unks_out, residuals
partial_eval_jaxpr_rules[xla_call_p] = xla_call_peval_eqn
通过这样,我们可以随心所欲地组合linearize和jit:
@jit
def f(x):
y = sin(x) * 2.
z = - y + x
return z
y, f_lin = linearize(f, 3.)
y_dot = f_lin(1.)
print(y, y_dot)
2.7177599838802657 2.979984993200891
@jit
def f(x):
y = sin(x) * 2.
z = g(x, y)
return z
@jit
def g(x, y):
return cos(x) + y
y, f_lin = linearize(f, 3.)
y_dot = f_lin(1.)
print(y, y_dot)
-0.7077524804807109 -2.121105001260758
vjp和grad
vjp变换的工作方式与线性化非常相似。其类型签名类似:
linearize : (a -> b) -> a -> (b, T a -o T b)
vjp : (a -> b) -> a -> (b, T b -o T a)
唯一的区别在于,我们在返回之前转置计算的线性部分,以便从类型T a -o T b变为类型T b -o T a。也就是说,我们将vjp实现为以下内容:
def vjp(f, x):
y, f_lin = linearize(f, x)
f_vjp = lambda y_bar: transpose(f_lin)(y_bar)
return y, f_vjp
由于我们将线性计算作为 jaxpr,而不仅仅是 Python 可调用的函数,因此我们可以将转置转换实现为 jaxpr 解释器。
def vjp_flat(f, *primals_in):
pvals_in = ([PartialVal.known(x) for x in primals_in] +
[PartialVal.unknown(vspace(get_aval(x))) for x in primals_in])
primal_pvals_in, tangent_pvals_in = split_half(pvals_in)
def f_jvp(*primals_tangents_in):
primals_out, tangents_out = jvp(f, *split_half(primals_tangents_in))
return [*primals_out, *tangents_out]
jaxpr, pvals_out, consts = partial_eval_flat(f_jvp, pvals_in) # linearize
primal_pvals, _ = split_half(pvals_out)
assert all(pval.is_known for pval in primal_pvals)
primals_out = [pval.const for pval in primal_pvals]
transpose_inputs = consts + [UndefPrimal(p.aval) for p in tangent_pvals_in]
f_vjp = lambda *cts: eval_jaxpr_transposed(jaxpr, transpose_inputs, cts)
return primals_out, f_vjp
def vjp(f, *primals_in):
primals_in_flat, in_tree = tree_flatten(primals_in)
f, out_tree = flatten_fun(f, in_tree)
primals_out_flat, f_vjp_flat = vjp_flat(f, *primals_in_flat)
primals_out = tree_unflatten(out_tree(), primals_out_flat)
def f_vjp(*cotangents_out):
cotangents_out_flat, _ = tree_flatten(cotangents_out)
cotangents_in_flat = f_vjp_flat(*cotangents_out_flat)
return tree_unflatten(in_tree, cotangents_in_flat)
return primals_out, f_vjp
class UndefPrimal(NamedTuple):
aval: ShapedArray
register_pytree_node(UndefPrimal,
lambda u: (u.aval, ()),
lambda aval, _: UndefPrimal(aval))
我们使用UndefPrimal实例来指示我们希望进行转置的参数。这是因为通常情况下,我们想要明确关闭值,我们希望将类型为a -> b -o c的函数转置为类型为a -> c -o b的函数。更一般地说,与函数线性相关的输入可能分散在参数列表中。因此,我们使用UndefPrimal指示线性位置。我们将UndefPrimal注册为一个 pytree 节点,因为 pytree 机制提供了一种方便的方法来从参数列表中剪除这些占位符。
接下来,我们可以编写eval_jaxpr_transposed,以及对所有至少可以线性的原语编写转置规则:
# NB: the analogous function in JAX is called 'backward_pass'
def eval_jaxpr_transposed(jaxpr: Jaxpr, args: list[Any], cotangents: list[Any]
) -> list[Any]:
primal_env: dict[Var, Any] = {}
ct_env: dict[Var, Any] = {}
def read_primal(x: Atom) -> Any:
return primal_env.get(x, UndefPrimal(x.aval)) if type(x) is Var else x.val
def write_primal(v: Var, val: Any) -> None:
if type(val) is not UndefPrimal:
primal_env[v] = val
def read_cotangent(v: Var) -> Any:
return ct_env.pop(v, np.zeros(v.aval.shape, v.aval.dtype))
def write_cotangent(x: Atom, val: Any):
if type(x) is Var and val is not None:
ct_env[x] = add(ct_env[x], val) if x in ct_env else val
map(write_primal, jaxpr.in_binders, args)
map(write_cotangent, jaxpr.outs, cotangents)
for eqn in jaxpr.eqns[::-1]:
primals_in = map(read_primal, eqn.inputs)
cts_in = map(read_cotangent, eqn.out_binders)
rule = transpose_rules[eqn.primitive]
cts_out = rule(cts_in, *primals_in, **eqn.params)
map(write_cotangent, eqn.inputs, cts_out)
return [read_cotangent(v) for v, x in zip(jaxpr.in_binders, args)
if type(x) is UndefPrimal]
transpose_rules = {}
def mul_transpose_rule(cts, x, y):
z_bar, = cts
assert (type(x) is UndefPrimal) ^ (type(y) is UndefPrimal)
return [mul(z_bar, y), None] if type(x) is UndefPrimal else [None, mul(x, z_bar)]
transpose_rules[mul_p] = mul_transpose_rule
def neg_transpose_rule(cts, x):
ybar, = cts
assert type(x) is UndefPrimal
return [neg(ybar)]
transpose_rules[neg_p] = neg_transpose_rule
def add_transpose_rule(cts, x, y):
z_bar, = cts
return [z_bar, z_bar]
transpose_rules[add_p] = add_transpose_rule
def reduce_sum_transpose_rule(cts, x, *, axis):
y_bar, = cts
return [broadcast(y_bar, x.aval.shape, axis)]
transpose_rules[reduce_sum_p] = reduce_sum_transpose_rule
def xla_call_transpose_rule(cts, *invals, jaxpr, num_consts):
del num_consts # Unused
undef_primals = [type(x) is UndefPrimal for x in invals]
transposed_jaxpr, new_consts = transpose_jaxpr(jaxpr, tuple(undef_primals))
residuals, _ = partition_list(undef_primals, invals)
outs = bind(xla_call_p, *new_consts, *residuals, *cts,
jaxpr=transposed_jaxpr, num_consts=len(new_consts))
outs = iter(outs)
return [next(outs) if undef else None for undef in undef_primals]
transpose_rules[xla_call_p] = xla_call_transpose_rule
@lru_cache()
def transpose_jaxpr(jaxpr: Jaxpr, undef_primals: tuple[bool, ...]
) -> tuple[Jaxpr, list[Any]]:
avals_in, avals_out = typecheck_jaxpr(jaxpr)
traceable = partial(eval_jaxpr_transposed, jaxpr)
args = [UndefPrimal(a) if u else a for a, u in zip(avals_in, undef_primals)]
trans_jaxpr, consts, _ = make_jaxpr(traceable, tuple(args), tuple(avals_out))
typecheck_jaxpr(trans_jaxpr)
return trans_jaxpr, consts
现在我们可以进行线性化和转置,最后我们可以编写grad:
def grad(f):
def gradfun(x, *xs):
y, f_vjp = vjp(f, x, *xs)
if np.shape(y) != (): raise TypeError
x_bar, *_ = f_vjp(np.ones(np.shape(y), np.result_type(y)))
return x_bar
return gradfun
y, f_vjp = vjp(sin, 3.)
print(f_vjp(1.), cos(3.))
(np.float64(-0.9899924966004454),) -0.9899924966004454
def f(x):
y = sin(x) * 2.
z = - y + x
return z
print(grad(f)(3.))
2.979984993200891
@jit
def f(x):
y = x * 2.
z = g(y)
return z
@jit
def g(x):
return cos(x) * 2.
print(grad(f)(3.))
1.1176619927957034
这里是一个组合性压力测试:
# from core_test.py fun_with_nested_calls_2
def foo(x):
@jit
def bar(y):
def baz(w):
q = jit(lambda x: y)(x)
q = q + jit(lambda: y)()
q = q + jit(lambda y: w + y)(y)
q = jit(lambda w: jit(sin)(x) * y)(1.0) + q
return q
p, t = jvp(baz, (x + 1.0,), (y,))
return t + (x * p)
return bar(x)
def assert_allclose(*vals):
for v1, v2 in zip(vals[:-1], vals[1:]):
np.testing.assert_allclose(v1, v2)
ans1 = f(3.)
ans2 = jit(f)(3.)
ans3, _ = jvp(f, (3.,), (5.,))
ans4, _ = jvp(jit(f), (3.,), (5.,))
assert_allclose(ans1, ans2, ans3, ans4)
deriv1 = grad(f)(3.)
deriv2 = grad(jit(f))(3.)
deriv3 = jit(grad(jit(f)))(3.)
_, deriv4 = jvp(f, (3.,), (1.,))
_, deriv5 = jvp(jit(f), (3.,), (1.,))
assert_allclose(deriv1, deriv2, deriv3, deriv4, deriv5)
hess1 = grad(grad(f))(3.)
hess2 = grad(grad(jit(f)))(3.)
hess3 = grad(jit(grad(f)))(3.)
hess4 = jit(grad(grad(f)))(3.)
_, hess5 = jvp(grad(f), (3.,), (1.,))
_, hess6 = jvp(jit(grad(f)), (3.,), (1.,))
_, hess7 = jvp(jit(grad(f)), (3.,), (1.,))
assert_allclose(hess1, hess2, hess3, hess4, hess5, hess6, hess7)
第五部分:控制流原语cond
接下来我们将添加用于暂停控制流的高阶原语。这类似于第三部分中的jit,另一个高阶原语,但它们不同之处在于它们是由多个可调用参数化的,而不仅仅是一个。
添加cond
我们引入了cond原语来表示在 jaxpr 中条件应用一个函数或另一个函数。我们用Bool -> (a -> b) -> (a -> b) -> a -> b来表示cond的类型。简而言之,cond接受一个代表谓词的布尔值和两个相同类型的函数。根据谓词的值,它将一个函数应用于最后一个参数。
在 Python 中,我们表示它为一个函数,它本身接受两个函数作为参数。与jit一样,第一步是在其可调用参数上调用make_jaxpr,将它们转换为 jaxprs:
def cond(pred, true_fn, false_fn, *operands):
avals_in = [raise_to_shaped(get_aval(x)) for x in operands]
true_jaxpr, true_consts, out_tree = make_jaxpr(true_fn, *avals_in)
false_jaxpr, false_consts, out_tree_ = make_jaxpr(false_fn, *avals_in)
if out_tree != out_tree_: raise TypeError
true_jaxpr, false_jaxpr = _join_jaxpr_consts(
true_jaxpr, false_jaxpr, len(true_consts), len(false_consts))
if typecheck_jaxpr(true_jaxpr) != typecheck_jaxpr(false_jaxpr):
raise TypeError
outs = bind_cond(pred, *true_consts, *false_consts, *operands,
true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
return tree_unflatten(out_tree, outs)
cond_p = Primitive('cond')
def _join_jaxpr_consts(jaxpr1: Jaxpr, jaxpr2: Jaxpr, n1: int, n2: int
) -> tuple[Jaxpr, Jaxpr]:
jaxpr1_type, jaxpr2_type = typecheck_jaxpr(jaxpr1), typecheck_jaxpr(jaxpr2)
assert jaxpr1_type.in_types[n1:] == jaxpr2_type.in_types[n2:]
consts1, rest1 = split_list(jaxpr1.in_binders, n1)
consts2, rest2 = split_list(jaxpr2.in_binders, n2)
new_jaxpr1 = Jaxpr(consts1 + consts2 + rest1, jaxpr1.eqns, jaxpr1.outs)
new_jaxpr2 = Jaxpr(consts1 + consts2 + rest2, jaxpr2.eqns, jaxpr2.outs)
return new_jaxpr1, new_jaxpr2
def bind_cond(pred, *args, true_jaxpr, false_jaxpr):
assert len(args) == len(true_jaxpr.in_binders) == len(false_jaxpr.in_binders)
return bind(cond_p, pred, *args, true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
我们要求true_jaxpr和false_jaxpr具有相同的类型,但是因为它们可能封闭于不同的常量(而且因为 jaxprs 只能表示封闭项,即不能有自由变量,而是闭包转换),我们需要使用辅助函数_join_jaxpr_consts来使这两个 jaxprs 的输入绑定列表一致。(为了更经济,我们可以尝试识别具有相同形状的常量对,但我们只是简单地连接常量列表。)
下一步,我们可以添加cond的解释规则。它的评估规则很简单:
def cond_impl(pred, *operands, true_jaxpr, false_jaxpr):
if pred:
return eval_jaxpr(true_jaxpr, operands)
else:
return eval_jaxpr(false_jaxpr, operands)
impl_rules[cond_p] = cond_impl
out = cond(True, lambda: 3, lambda: 4)
print(out)
3
对于它的 JVP 和 vmap 规则,我们只需要调用我们为jit创建的相同的jvp_jaxpr和vmap_jaxpr实用程序,然后再次使用_join_jaxpr_consts:
def cond_jvp_rule(primals, tangents, *, true_jaxpr, false_jaxpr):
pred, *primals = primals
_ , *tangents = tangents
true_jaxpr , true_consts = jvp_jaxpr(true_jaxpr)
false_jaxpr, false_consts = jvp_jaxpr(false_jaxpr)
true_jaxpr, false_jaxpr = _join_jaxpr_consts(
true_jaxpr, false_jaxpr, len(true_consts), len(false_consts))
assert typecheck_jaxpr(true_jaxpr) == typecheck_jaxpr(false_jaxpr)
outs = bind_cond(pred, *true_consts, *false_consts, *primals, *tangents,
true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
primals_out, tangents_out = split_half(outs)
return primals_out, tangents_out
jvp_rules[cond_p] = cond_jvp_rule
out, out_tan = jvp(lambda x: cond(True, lambda: x * x, lambda: 0.), (1.,), (1.,))
print(out_tan)
2.0
def cond_vmap_rule(axis_size, vals_in, dims_in, *, true_jaxpr, false_jaxpr):
pred , *vals_in = vals_in
pred_dim, *dims_in = dims_in
if pred_dim is not not_mapped: raise NotImplementedError # TODO
true_jaxpr, true_consts = vmap_jaxpr(true_jaxpr, axis_size, tuple(dims_in))
false_jaxpr, false_consts = vmap_jaxpr(false_jaxpr, axis_size, tuple(dims_in))
true_jaxpr, false_jaxpr = _join_jaxpr_consts(
true_jaxpr, false_jaxpr, len(true_consts), len(false_consts))
assert typecheck_jaxpr(true_jaxpr) == typecheck_jaxpr(false_jaxpr)
outs = bind_cond(pred, *true_consts, *false_consts, *vals_in,
true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
return outs, [0] * len(outs)
vmap_rules[cond_p] = cond_vmap_rule
xs = np.array([1., 2., 3])
out = vmap(lambda x: cond(True, lambda: x + 1., lambda: 0.), (0,))(xs)
print(out)
[2\. 3\. 4.]
请注意,目前我们不支持谓词值本身是批量化的情况。在 JAX 的主流版本中,我们通过将条件转换成选择原语来处理这种情况。只要true_fun和false_fun不涉及任何产生副作用的原语,这种转换在语义上是正确的。
这里没有表现出来的另一件事,但在主流 JAX 中存在的是,将两个相同类型的 jaxprs 进行转换可能导致不同类型的 jaxprs。例如,将vmap_jaxpr的主流 JAX 版本应用于恒等函数 jaxpr
{ lambda a:float32[] .
let
in ( a ) }
将导致一个带有批处理输出的 jaxpr,类型为[float32[10]] -> [float32[10]],如果批处理大小为 10,而将其应用于零函数 jaxpr
{ lambda a:float32[] .
let
in ( 0. ) }
会导致一个带有未批处理输出的 jaxpr,类型为[float32[10]] -> [float32[]]。这是一种优化,旨在不必要地组合值。但这意味着在cond中,我们需要额外的步骤来连接两个转换后的 jaxprs 以获得一致的输出类型。我们不需要在这里进行这一步,因为我们选择了一直在主导轴上批处理所有输出的vmap_jaxpr。
下一步,我们可以转向抽象评估和 XLA 降级规则:
def cond_abstract_eval(pred_type, *in_types, true_jaxpr, false_jaxpr):
if pred_type != ShapedArray((), np.dtype('bool')): raise TypeError
jaxpr_type = typecheck_jaxpr(true_jaxpr)
if jaxpr_type != typecheck_jaxpr(false_jaxpr):
raise TypeError
if not all(t1 == t2 for t1, t2 in zip(jaxpr_type.in_types, in_types)):
raise TypeError
return jaxpr_type.out_types
abstract_eval_rules[cond_p] = cond_abstract_eval
def cond_translation(c, in_avals, in_vals, *, true_jaxpr, false_jaxpr):
del in_avals # Unused
pred, *in_vals = in_vals
flat_vals, in_tree = tree_flatten(in_vals)
operand = xops.Tuple(c, flat_vals)
operand_shape = c.get_shape(operand)
def make_comp(name: str, jaxpr: Jaxpr) -> xe.XlaComputation:
c = xc.XlaBuilder(name)
operand = xops.Parameter(c, 0, operand_shape)
operands = tree_unflatten(in_tree, destructure_tuple(c, operand))
outs = jaxpr_subcomp(c, jaxpr, operands)
return c.build(xops.Tuple(c, outs))
true_comp = make_comp('true_fn', true_jaxpr)
false_comp = make_comp('false_fn', false_jaxpr)
int_etype = xc.dtype_to_etype(np.dtype('int32'))
out = xops.Conditional(xops.ConvertElementType(pred, int_etype),
[false_comp, true_comp], [operand] * 2)
return destructure_tuple(c, out)
xla_translations[cond_p] = cond_translation
out = jit(lambda: cond(False, lambda: 1, lambda: 2))()
print(out)
2
最后,为了支持反向模式自动微分,我们需要部分评估和转置规则。对于部分评估,我们需要引入另一个 jaxpr-munging 实用程序 _join_jaxpr_res,以处理应用于 true_fun 和 false_fun 的部分评估通常会导致不同的残余。我们使用 _join_jaxpr_res 使转换后的 jaxprs 的输出类型保持一致(而 _join_jaxpr_consts 处理了输入类型)。
def cond_partial_eval(trace, tracers, *, true_jaxpr, false_jaxpr):
pred_tracer, *tracers = tracers
assert pred_tracer.pval.is_known
pred = pred_tracer.pval.const
in_uks = [not t.pval.is_known for t in tracers]
*jaxprs, out_uks, num_res = _cond_partial_eval(true_jaxpr, false_jaxpr, in_uks)
t_jaxpr1, f_jaxpr1, t_jaxpr2, f_jaxpr2 = jaxprs
known_tracers, unknown_tracers = partition_list(in_uks, tracers)
known_vals = [t.pval.const for t in known_tracers]
outs1_res = bind_cond(pred, *known_vals,
true_jaxpr=t_jaxpr1, false_jaxpr=f_jaxpr1)
outs1, res = split_list(outs1_res, len(outs1_res) - num_res)
pred_tracer_ = trace.instantiate_const(full_raise(trace, pred_tracer))
res_tracers = [trace.instantiate_const(full_raise(trace, x)) for x in res]
outs2 = [PartialEvalTracer(trace, PartialVal.unknown(v.aval), None)
for v in t_jaxpr2.outs]
eqn = JaxprEqnRecipe(cond_p, [pred_tracer_, *res_tracers, *unknown_tracers],
dict(true_jaxpr=t_jaxpr2, false_jaxpr=f_jaxpr2),
[v.aval for v in t_jaxpr2.outs], map(ref, outs2))
for t in outs2: t.recipe = eqn
return merge_lists(out_uks, outs1, outs2)
partial_eval_rules[cond_p] = cond_partial_eval
def _cond_partial_eval(true_jaxpr: Jaxpr, false_jaxpr: Jaxpr, in_uks: list[bool]
) -> tuple[Jaxpr, Jaxpr, Jaxpr, Jaxpr, list[bool], int]:
_, _, t_out_uks, _ = partial_eval_jaxpr(true_jaxpr , in_uks)
_, _, f_out_uks, _ = partial_eval_jaxpr(false_jaxpr, in_uks)
out_uks = map(op.or_, t_out_uks, f_out_uks)
t_jaxpr1, t_jaxpr2, _, t_nres = partial_eval_jaxpr(true_jaxpr , in_uks, out_uks)
f_jaxpr1, f_jaxpr2, _, f_nres = partial_eval_jaxpr(false_jaxpr, in_uks, out_uks)
t_jaxpr1, f_jaxpr1 = _join_jaxpr_res(t_jaxpr1, f_jaxpr1, t_nres, f_nres)
t_jaxpr2, f_jaxpr2 = _join_jaxpr_consts(t_jaxpr2, f_jaxpr2, t_nres, f_nres)
assert typecheck_jaxpr(t_jaxpr1) == typecheck_jaxpr(f_jaxpr1)
assert typecheck_jaxpr(t_jaxpr2) == typecheck_jaxpr(f_jaxpr2)
num_res = t_nres + f_nres
return t_jaxpr1, f_jaxpr1, t_jaxpr2, f_jaxpr2, out_uks, num_res
def _join_jaxpr_res(jaxpr1: Jaxpr, jaxpr2: Jaxpr, n1: int, n2: int
) -> tuple[Jaxpr, Jaxpr]:
jaxpr1_type, jaxpr2_type = typecheck_jaxpr(jaxpr1), typecheck_jaxpr(jaxpr2)
out_types1, _ = split_list(jaxpr1_type.out_types, len(jaxpr1.outs) - n1)
out_types2, _ = split_list(jaxpr2_type.out_types, len(jaxpr2.outs) - n2)
assert out_types1 == out_types2
outs1, res1 = split_list(jaxpr1.outs, len(jaxpr1.outs) - n1)
outs2, res2 = split_list(jaxpr2.outs, len(jaxpr2.outs) - n2)
zeros_like1 = [Lit(np.zeros(v.aval.shape, v.aval.dtype)) for v in res1]
zeros_like2 = [Lit(np.zeros(v.aval.shape, v.aval.dtype)) for v in res2]
new_jaxpr1 = Jaxpr(jaxpr1.in_binders, jaxpr1.eqns, outs1 + res1 + zeros_like2)
new_jaxpr2 = Jaxpr(jaxpr2.in_binders, jaxpr2.eqns, outs2 + zeros_like1 + res2)
return new_jaxpr1, new_jaxpr2
_, f_lin = linearize(lambda x: cond(True, lambda: x, lambda: 0.), 1.)
out = f_lin(3.14)
print(out)
3.14
def cond_peval_eqn(unks_in: list[bool], eqn: JaxprEqn,
) -> tuple[JaxprEqn, JaxprEqn, list[bool], list[Atom]]:
pred_unk, *unks_in = unks_in
assert not pred_unk
true_jaxpr, false_jaxpr = eqn.params['true_jaxpr'], eqn.params['false_jaxpr']
*jaxprs, unks_out, num_res = _cond_partial_eval(true_jaxpr, false_jaxpr, unks_in)
t_jaxpr1, f_jaxpr1, t_jaxpr2, f_jaxpr2 = jaxprs
ins1, ins2 = partition_list(unks_in, eqn.inputs[1:])
outs1, outs2 = partition_list(unks_out, eqn.out_binders)
residuals, _ = split_list(t_jaxpr2.in_binders, num_res)
eqn1 = JaxprEqn(cond_p, [eqn.inputs[0], *ins1],
dict(true_jaxpr=t_jaxpr1, false_jaxpr=f_jaxpr1),
outs1 + residuals)
eqn2 = JaxprEqn(cond_p, [eqn.inputs[0], *residuals, *ins2],
dict(true_jaxpr=t_jaxpr2, false_jaxpr=f_jaxpr2),
outs2)
res = [eqn.inputs[0], *residuals] if type(eqn.inputs[0]) is Var else residuals
return eqn1, eqn2, unks_out, res
partial_eval_jaxpr_rules[cond_p] = cond_peval_eqn
_, f_lin = linearize(jit(lambda x: cond(True, lambda: x, lambda: 0.)), 1.)
out = f_lin(3.14)
print(out)
3.14
转置是 transpose_jaxpr 的一个相当简单的应用:
def cond_transpose_rule(cts, pred, *invals, true_jaxpr, false_jaxpr):
undef_primals = tuple(type(x) is UndefPrimal for x in invals)
true_jaxpr, true_consts = transpose_jaxpr(true_jaxpr, undef_primals)
false_jaxpr, false_consts = transpose_jaxpr(false_jaxpr, undef_primals)
true_jaxpr, false_jaxpr = _join_jaxpr_consts(
true_jaxpr, false_jaxpr, len(true_consts), len(false_consts))
res = [x for x in invals if type(x) is not UndefPrimal]
outs = bind_cond(pred, *true_consts, *false_consts, *res, *cts,
true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
outs = iter(outs)
return [None] + [next(outs) if type(x) is UndefPrimal else None for x in invals]
transpose_rules[cond_p] = cond_transpose_rule
out = grad(lambda x: cond(True, lambda: x * x, lambda: 0.))(1.)
print(out)
2.0
def pprint_cond(names: defaultdict[Var, str], eqn: JaxprEqn) -> PPrint:
true_jaxpr, false_jaxpr = eqn.params['true_jaxpr'], eqn.params['false_jaxpr']
new_params = {k:v for k, v in eqn.params.items() if not k.endswith('jaxpr')}
lhs = pp(' '.join(var_str(names, v) for v in eqn.out_binders))
rhs = (pp(eqn.primitive.name) >> pp_params(new_params) >>
pp(' '.join(names[x] if isinstance(x, Var) else str(x.val)
for x in eqn.inputs)))
return vcat([lhs >> pp(' = ') >> rhs,
pp_jaxpr(true_jaxpr).indent(2),
pp_jaxpr(false_jaxpr).indent(2)])
pp_rules[cond_p] = pprint_cond
```</details>
jaxpr_res(jaxpr1: Jaxpr, jaxpr2: Jaxpr, n1: int, n2: int
) -> tuple[Jaxpr, Jaxpr]:
jaxpr1_type, jaxpr2_type = typecheck_jaxpr(jaxpr1), typecheck_jaxpr(jaxpr2)
out_types1, _ = split_list(jaxpr1_type.out_types, len(jaxpr1.outs) - n1)
out_types2, _ = split_list(jaxpr2_type.out_types, len(jaxpr2.outs) - n2)
assert out_types1 == out_types2
outs1, res1 = split_list(jaxpr1.outs, len(jaxpr1.outs) - n1)
outs2, res2 = split_list(jaxpr2.outs, len(jaxpr2.outs) - n2)
zeros_like1 = [Lit(np.zeros(v.aval.shape, v.aval.dtype)) for v in res1]
zeros_like2 = [Lit(np.zeros(v.aval.shape, v.aval.dtype)) for v in res2]
new_jaxpr1 = Jaxpr(jaxpr1.in_binders, jaxpr1.eqns, outs1 + res1 + zeros_like2)
new_jaxpr2 = Jaxpr(jaxpr2.in_binders, jaxpr2.eqns, outs2 + zeros_like1 + res2)
return new_jaxpr1, new_jaxpr2
_, f_lin = linearize(lambda x: cond(True, lambda: x, lambda: 0.), 1.)
out = f_lin(3.14)
print(out)
3.14
def cond_peval_eqn(unks_in: list[bool], eqn: JaxprEqn,
) -> tuple[JaxprEqn, JaxprEqn, list[bool], list[Atom]]:
pred_unk, *unks_in = unks_in
assert not pred_unk
true_jaxpr, false_jaxpr = eqn.params['true_jaxpr'], eqn.params['false_jaxpr']
*jaxprs, unks_out, num_res = _cond_partial_eval(true_jaxpr, false_jaxpr, unks_in)
t_jaxpr1, f_jaxpr1, t_jaxpr2, f_jaxpr2 = jaxprs
ins1, ins2 = partition_list(unks_in, eqn.inputs[1:])
outs1, outs2 = partition_list(unks_out, eqn.out_binders)
residuals, _ = split_list(t_jaxpr2.in_binders, num_res)
eqn1 = JaxprEqn(cond_p, [eqn.inputs[0], *ins1],
dict(true_jaxpr=t_jaxpr1, false_jaxpr=f_jaxpr1),
outs1 + residuals)
eqn2 = JaxprEqn(cond_p, [eqn.inputs[0], *residuals, *ins2],
dict(true_jaxpr=t_jaxpr2, false_jaxpr=f_jaxpr2),
outs2)
res = [eqn.inputs[0], *residuals] if type(eqn.inputs[0]) is Var else residuals
return eqn1, eqn2, unks_out, res
partial_eval_jaxpr_rules[cond_p] = cond_peval_eqn
_, f_lin = linearize(jit(lambda x: cond(True, lambda: x, lambda: 0.)), 1.)
out = f_lin(3.14)
print(out)
3.14
转置是 transpose_jaxpr 的一个相当简单的应用:
def cond_transpose_rule(cts, pred, *invals, true_jaxpr, false_jaxpr):
undef_primals = tuple(type(x) is UndefPrimal for x in invals)
true_jaxpr, true_consts = transpose_jaxpr(true_jaxpr, undef_primals)
false_jaxpr, false_consts = transpose_jaxpr(false_jaxpr, undef_primals)
true_jaxpr, false_jaxpr = _join_jaxpr_consts(
true_jaxpr, false_jaxpr, len(true_consts), len(false_consts))
res = [x for x in invals if type(x) is not UndefPrimal]
outs = bind_cond(pred, *true_consts, *false_consts, *res, *cts,
true_jaxpr=true_jaxpr, false_jaxpr=false_jaxpr)
outs = iter(outs)
return [None] + [next(outs) if type(x) is UndefPrimal else None for x in invals]
transpose_rules[cond_p] = cond_transpose_rule
out = grad(lambda x: cond(True, lambda: x * x, lambda: 0.))(1.)
print(out)
2.0
def pprint_cond(names: defaultdict[Var, str], eqn: JaxprEqn) -> PPrint:
true_jaxpr, false_jaxpr = eqn.params['true_jaxpr'], eqn.params['false_jaxpr']
new_params = {k:v for k, v in eqn.params.items() if not k.endswith('jaxpr')}
lhs = pp(' '.join(var_str(names, v) for v in eqn.out_binders))
rhs = (pp(eqn.primitive.name) >> pp_params(new_params) >>
pp(' '.join(names[x] if isinstance(x, Var) else str(x.val)
for x in eqn.inputs)))
return vcat([lhs >> pp(' = ') >> rhs,
pp_jaxpr(true_jaxpr).indent(2),
pp_jaxpr(false_jaxpr).indent(2)])
pp_rules[cond_p] = pprint_cond
```</details>

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








