Machine Learning Mastery LSTM 教程（三）

原文：Machine Learning Mastery

协议：CC BY-NC-SA 4.0

如何使用编解码器 LSTM 来打印随机整数序列

原文： machinelearningmastery.com/how-to-use-an-encoder-decoder-lstm-to-echo-sequences-of-random-integers/

长短期记忆（LSTM）循环神经网络的一个强大功能是它们可以记住长序列间隔的观察结果。

这可以通过设计简单的序列回波问题来证明，其中输入序列的整个输入序列或部分连续块作为输出序列被回应。

开发 LSTM 循环神经网络以解决序列回波问题既是 LSTM 功能的良好证明，也可用于演示最先进的循环神经网络架构。

在这篇文章中，您将了解如何开发 LSTM 以使用 Keras 深度学习库解决 Python 中的完整和部分序列打印问题。

完成本教程后，您将了解：

• 如何生成随机的整数序列，使用单热编码表示它们，并将序列构建为具有输入和输出对的监督学习问题。
• 如何开发序列到序列 LSTM 以将整个输入序列作为输出进行打印。
• 如何开发编解码器 LSTM 以打印长度与输入序列不同的部分序列。

让我们开始吧。

如何使用编解码器 LSTM 来回放随机整数序列
照片来自 hammy24601 ，保留一些权利。

概观

本教程分为 3 个部分;他们是：

1. 序列回波问题
2. 打印整个序列（序列到序列模型）
3. 打印部分序列（编解码器模型）

环境

本教程假定您已安装 Python SciPy 环境。您可以在此示例中使用 Python 2 或 3。

本教程假设您安装了 TensorFlow 或 Theano 后端的 Keras v2.0 或更高版本。

本教程还假设您安装了 scikit-learn，Pandas，NumPy 和 Matplotlib。

如果您在设置 Python 环境时需要帮助，请参阅以下帖子：

• 如何使用 Anaconda 设置用于机器学习和深度学习的 Python 环境

序列回波问题

回波序列问题涉及将 LSTM 暴露于一系列观察中，一次一个，然后要求网络打印观察到的部分或完整的连续观察列表。

这迫使网络记住连续观测的块，并且是 LSTM 循环神经网络学习能力的一个很好的证明。

第一步是编写一些代码来生成随机的整数序列，并为网络编码。

这涉及 3 个步骤：

1. 生成随机序列
2. 单热编码随机序列
3. 用于学习的帧编码序列

生成随机序列

我们可以使用 randint（）函数在 Python 中生成随机整数，该函数接受两个参数，指示从中绘制值的整数范围。

在本教程中，我们将问题定义为具有 0 到 99 之间的整数值以及 100 个唯一值。

randint(0, 99)

我们可以将它放在一个名为 generate_sequence（）的函数中，该函数将生成所需长度的随机整数序列，默认长度设置为 25 个元素。

此功能如下所列。

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

单热编码随机序列

一旦我们生成了随机整数序列，我们需要将它们转换为适合训练 LSTM 网络的格式。

一种选择是将整数重新缩放到范围[0,1]。这可行，并要求将问题表述为回归。

我有兴趣预测正确的数字，而不是接近预期值的数字。这意味着我更倾向于将问题框架化为分类而不是回归，其中预期输出是一个类，并且有 100 个可能的类值。

在这种情况下，我们可以使用整数值的单热编码，其中每个值由 100 个元素的二进制向量表示，除了整数的索引（标记为 1）之外，该二进制向量都是“0”值。

下面的函数 one_hot_encode（）定义了如何迭代整数序列并为每个整数创建二进制向量表示，并将结果作为二维数组返回。

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

我们还需要解码编码值，以便我们可以使用预测，在这种情况下，只需查看它们。

可以通过使用 argmax（）NumPy 函数来反转单热编码，该函数返回具有最大值的向量中的值的索引。

下面的函数名为 one_hot_decode（），将对编码序列进行解码，并可用于稍后解码来自我们网络的预测。

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

用于学习的帧编码序列

一旦生成并编码了序列，就必须将它们组织成适合学习的框架。

这涉及将线性序列组织成输入（X）和输出（y）对。

例如，序列[1,2,3,4,5]可以被构造为具有 2 个输入（t 和 t-1）和 1 个输出（t-1）的序列预测问题，如下所示：

X,			y
NaN, 1,		NaN
1, 2,		1
2, 3,		2
3, 4,		3
4, 5,		4
5, NaN,		5

请注意，缺少数据标有 NaN 值。这些行可以用特殊字符填充并屏蔽。或者，更简单地说，可以从数据集中移除这些行，代价是从要学习的序列中提供更少的示例。后一种方法将是本例中使用的方法。

我们将使用 Pandas shift（）函数来创建编码序列的移位版本。使用 dropna（）函数删除缺少数据的行。

然后，我们可以从移位的数据帧中指定输入和输出数据。数据必须是 3 维的，以用于序列预测 LSTM。输入和输出都需要维度[样本，时间步长，特征]，其中样本是行数，时间步长是从中学习预测的滞后观察数，而特征是单独值的数量（例如 100 单热门编码）。

下面的代码定义了实现此功能的 to_supervised（）函数。它需要两个参数来指定用作输入和输出的编码整数的数量。输出整数的数量必须小于或等于输入的数量，并从最早的观察计算。

例如，如果在序列[1,2,3,4,5]上为输入和输出指定了 5 和 1，那么该函数将返回 X 中的单行[1,2,3,4,5]和[1]中的 y 一行。

# convert encoded sequence to supervised learning
def to_supervised(sequence, n_in, n_out):
	# create lag copies of the sequence
	df = DataFrame(sequence)
	df = concat([df.shift(n_in-i-1) for i in range(n_in)], axis=1)
	# drop rows with missing values
	df.dropna(inplace=True)
	# specify columns for input and output pairs
	values = df.values
	width = sequence.shape[1]
	X = values.reshape(len(values), n_in, width)
	y = values[:, 0:(n_out*width)].reshape(len(values), n_out, width)
	return X, y

有关将序列转换为监督学习问题的更多信息，请参阅帖子：

• 时间序列预测作为监督学习
• 如何将时间序列转换为 Python 中的监督学习问题

完整的例子

我们可以将所有这些结合在一起。

下面是完整的代码清单，用于生成 25 个随机整数的序列，并将每个整数编码为二进制向量，将它们分成 X，y 对进行学习，然后打印解码对以供查看。

from random import randint
from numpy import array
from numpy import argmax
from pandas import DataFrame
from pandas import concat

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# convert encoded sequence to supervised learning
def to_supervised(sequence, n_in, n_out):
	# create lag copies of the sequence
	df = DataFrame(sequence)
	df = concat([df.shift(n_in-i-1) for i in range(n_in)], axis=1)
	# drop rows with missing values
	df.dropna(inplace=True)
	# specify columns for input and output pairs
	values = df.values
	width = sequence.shape[1]
	X = values.reshape(len(values), n_in, width)
	y = values[:, 0:(n_out*width)].reshape(len(values), n_out, width)
	return X, y

# generate random sequence
sequence = generate_sequence()
print(sequence)
# one hot encode
encoded = one_hot_encode(sequence)
# convert to X,y pairs
X,y = to_supervised(encoded, 5, 3)
# decode all pairs
for i in range(len(X)):
	print(one_hot_decode(X[i]), '=>', one_hot_decode(y[i]))

运行示例可能会为您生成不同的特定数字。

将序列分成 5 个数字的输入序列，并输出来自输入序列的 3 个最老观察结果的序列。

[86, 81, 88, 1, 23, 78, 64, 7, 99, 23, 2, 36, 73, 26, 27, 33, 24, 51, 73, 64, 13, 13, 53, 40, 64]

[86, 81, 88, 1, 23] => [86, 81, 88]
[81, 88, 1, 23, 78] => [81, 88, 1]
[88, 1, 23, 78, 64] => [88, 1, 23]
[1, 23, 78, 64, 7] => [1, 23, 78]
[23, 78, 64, 7, 99] => [23, 78, 64]
[78, 64, 7, 99, 23] => [78, 64, 7]
[64, 7, 99, 23, 2] => [64, 7, 99]
[7, 99, 23, 2, 36] => [7, 99, 23]
[99, 23, 2, 36, 73] => [99, 23, 2]
[23, 2, 36, 73, 26] => [23, 2, 36]
[2, 36, 73, 26, 27] => [2, 36, 73]
[36, 73, 26, 27, 33] => [36, 73, 26]
[73, 26, 27, 33, 24] => [73, 26, 27]
[26, 27, 33, 24, 51] => [26, 27, 33]
[27, 33, 24, 51, 73] => [27, 33, 24]
[33, 24, 51, 73, 64] => [33, 24, 51]
[24, 51, 73, 64, 13] => [24, 51, 73]
[51, 73, 64, 13, 13] => [51, 73, 64]
[73, 64, 13, 13, 53] => [73, 64, 13]
[64, 13, 13, 53, 40] => [64, 13, 13]
[13, 13, 53, 40, 64] => [13, 13, 53]

现在我们知道如何准备和表示整数的随机序列，我们可以看一下使用 LSTM 来学习它们。

打印全序列

（_ 序列到序列模型 _）

在本节中，我们将开发一个 LSTM，用于简单地解决问题，即预测或再现整个输入序列。

也就是说，给定固定的输入序列，例如 5 个随机整数，输出相同的序列。这可能听起来不像问题的简单框架，但这是因为解决它所需的网络架构很简单。

我们将生成 25 个整数的随机序列，并将它们构造为 5 个值的输入 - 输出对。我们将创建一个名为 get_data（）的便捷函数，我们将使用它来创建编码的 X，y 对随机整数，使用上一节中准备的所有功能。此功能如下所列。

# prepare data for the LSTM
def get_data(n_in, n_out):
	# generate random sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# convert to X,y pairs
	X,y = to_supervised(encoded, n_in, n_out)
	return X,y

将使用参数 5 和 5 调用此函数，以创建 21 个样本，其中 5 个步骤的 100 个特征作为输入，并且与输出相同（21 个而不是 25 个，因为删除了由于序列移位而导致缺失值的某些行）。

我们现在可以为此问题开发 LSTM。我们将使用有状态 LSTM 并在训练结束时为每个生成的样本显式重置内部状态。由于学习所需的上下文将作为时间步长提供，因此可能需要或可能不需要跨序列中的样本维持网络内的内部状态;尽管如此，这个额外的状态可能会有所帮助。

让我们首先将输入数据的预期尺寸定义为 100 个特征的 5 个时间步长。因为我们使用有状态 LSTM，所以将使用 batch_input_shape 参数而不是 input_shape 指定。 LSTM 隐藏层将使用 20 个内存单元，这应该足以学习这个问题。

批量大小为 7。批量大小必须是训练样本数量的因子（在这种情况下为 21），并定义数量样本，之后更新 LSTM 中的权重。这意味着对于训练网络的每个随机序列，权重将更新 3 次。

model = Sequential()
model.add(LSTM(20, batch_input_shape=(7, 5, 100), return_sequences=True, stateful=True))

我们希望输出层一次输出一个整数，每个输出观察一个。

我们将输出层定义为完全连接的层（Dense），其中 100 个神经元用于单热编码中的 100 个可能的整数值中的每一个。因为我们使用单热编码并将问题框架化为多分类，所以我们可以在 Dense 层中使用 softmax 激活函数。

Dense(100, activation='softmax')

我们需要将此输出层包装在 TimeDistributed 层中。这是为了确保我们可以使用输出层为输入序列中的每个项目预测一个整数。这是关键，因此我们正在实现真正的多对多模型（例如序列到序列），而不是多对一模型，其中基于内部状态和值创建一次性向量输出输入序列中最后一次观察的结果（例如，输出层一次输出 5 * 100 个值）。

这要求先前的 LSTM 层通过设置 return_sequences = True 来返回序列（例如，输入序列中的每个观察的一个输出而不是整个输入序列的一个输出）。 TimeDistributed 层执行将来自 LSTM 层的序列的每个切片应用为包装的 Dense 层的输入的技巧，以便一次可以预测一个整数。

model.add(TimeDistributed(Dense(100, activation='softmax')))

我们将使用适用于多分类问题的日志丢失函数（categorical_crossentropy）和具有默认超参数的高效 ADAM 优化算法。

除了报告每个时期的日志损失之外，我们还将报告分类准确率，以了解我们的模型是如何训练的。

model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])

为了确保网络不记住问题，并且网络学习为所有可能的输入序列推广解决方案，我们将在每个训练时期生成新的随机序列。 LSTM 隐藏层内的内部状态将在每个时期结束时重置。我们将为 500 个训练时期拟合模型。

# train LSTM
for epoch in range(500):
	# generate new random sequence
	X,y = get_data(5, 5)
	# fit model for one epoch on this sequence
	model.fit(X, y, epochs=1, batch_size=7, verbose=2, shuffle=False)
	model.reset_states()

一旦拟合，我们将通过对一个新的整数随机序列做出预测来评估模型，并将解码的预期输出序列与预测的序列进行比较。

# evaluate LSTM
X,y = get_data(5, 5)
yhat = model.predict(X, batch_size=7, verbose=0)
# decode all pairs
for i in range(len(X)):
	print('Expected:', one_hot_decode(y[i]), 'Predicted', one_hot_decode(yhat[i]))

综合这些，下面提供了完整的代码清单。

from random import randint
from numpy import array
from numpy import argmax
from pandas import DataFrame
from pandas import concat
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import TimeDistributed

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# convert encoded sequence to supervised learning
def to_supervised(sequence, n_in, n_out):
	# create lag copies of the sequence
	df = DataFrame(sequence)
	df = concat([df.shift(n_in-i-1) for i in range(n_in)], axis=1)
	# drop rows with missing values
	df.dropna(inplace=True)
	# specify columns for input and output pairs
	values = df.values
	width = sequence.shape[1]
	X = values.reshape(len(values), n_in, width)
	y = values[:, 0:(n_out*width)].reshape(len(values), n_out, width)
	return X, y

# prepare data for the LSTM
def get_data(n_in, n_out):
	# generate random sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# convert to X,y pairs
	X,y = to_supervised(encoded, n_in, n_out)
	return X,y

# define LSTM
n_in = 5
n_out = 5
encoded_length = 100
batch_size = 7
model = Sequential()
model.add(LSTM(20, batch_input_shape=(batch_size, n_in, encoded_length), return_sequences=True, stateful=True))
model.add(TimeDistributed(Dense(encoded_length, activation='softmax')))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
# train LSTM
for epoch in range(500):
	# generate new random sequence
	X,y = get_data(n_in, n_out)
	# fit model for one epoch on this sequence
	model.fit(X, y, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
	model.reset_states()
# evaluate LSTM
X,y = get_data(n_in, n_out)
yhat = model.predict(X, batch_size=batch_size, verbose=0)
# decode all pairs
for i in range(len(X)):
	print('Expected:', one_hot_decode(y[i]), 'Predicted', one_hot_decode(yhat[i]))

运行该示例会在每个时期打印日志丢失和准确率。通过生成新的随机序列并将预期序列与预测序列进行比较来结束运行。

根据所选择的配置，每次运行时，网络几乎都会收敛到 100％的准确度。请注意，您可能会看到不同的最终序列和最终的日志丢失。

...
Epoch 1/1
0s - loss: 1.7310 - acc: 1.0000
Epoch 1/1
0s - loss: 1.5712 - acc: 1.0000
Epoch 1/1
0s - loss: 1.7447 - acc: 1.0000
Epoch 1/1
0s - loss: 1.5704 - acc: 1.0000
Epoch 1/1
0s - loss: 1.6124 - acc: 1.0000
Expected: [98, 30, 98, 11, 49] Predicted [98, 30, 98, 11, 49]
Expected: [30, 98, 11, 49, 1] Predicted [30, 98, 11, 49, 1]
Expected: [98, 11, 49, 1, 77] Predicted [98, 11, 49, 1, 77]
Expected: [11, 49, 1, 77, 80] Predicted [11, 49, 1, 77, 80]
Expected: [49, 1, 77, 80, 23] Predicted [49, 1, 77, 80, 23]
Expected: [1, 77, 80, 23, 32] Predicted [1, 77, 80, 23, 32]
Expected: [77, 80, 23, 32, 27] Predicted [77, 80, 23, 32, 27]
Expected: [80, 23, 32, 27, 66] Predicted [80, 23, 32, 27, 66]
Expected: [23, 32, 27, 66, 96] Predicted [23, 32, 27, 66, 96]
Expected: [32, 27, 66, 96, 76] Predicted [32, 27, 66, 96, 76]
Expected: [27, 66, 96, 76, 10] Predicted [27, 66, 96, 76, 10]
Expected: [66, 96, 76, 10, 39] Predicted [66, 96, 76, 10, 39]
Expected: [96, 76, 10, 39, 44] Predicted [96, 76, 10, 39, 44]
Expected: [76, 10, 39, 44, 57] Predicted [76, 10, 39, 44, 57]
Expected: [10, 39, 44, 57, 11] Predicted [10, 39, 44, 57, 11]
Expected: [39, 44, 57, 11, 48] Predicted [39, 44, 57, 11, 48]
Expected: [44, 57, 11, 48, 39] Predicted [44, 57, 11, 48, 39]
Expected: [57, 11, 48, 39, 28] Predicted [57, 11, 48, 39, 28]
Expected: [11, 48, 39, 28, 15] Predicted [11, 48, 39, 28, 15]
Expected: [48, 39, 28, 15, 49] Predicted [48, 39, 28, 15, 49]
Expected: [39, 28, 15, 49, 76] Predicted [39, 28, 15, 49, 76]

打印部分序列

（_ 编解码器模型 _）

到目前为止，这么好，但是如果我们希望输出序列的长度与输入序列的长度不同呢？

也就是说，我们希望从 5 个观测值的输入序列中打印前 2 个观测值：

[1, 2, 3, 4, 5] => [1, 2]

这仍然是序列到序列预测问题，但需要更改网络架构。

一种方法是使输出序列具有相同的长度，并使用填充将输出序列填充到相同的长度。

或者，我们可以使用更优雅的解决方案。我们可以实现允许可变长度输出的编解码器网络，其中编码器学习输入序列的内部表示，并且解码器读取内部表示并学习如何创建相同或不同长度的输出序列。

对于网络来说，这是一个更具挑战性的问题，并且需要额外的容量（更多的内存单元）和更长的训练（更多的时期）。

网络的输入，第一个隐藏的 LSTM 层和 TimeDistributed 密集输出层保持不变，除了我们将内存单元的数量从 20 增加到 150.我们还将批量大小从 7 增加到 21，以便重量更新是在随机序列的所有样本的末尾执行。经过一些实验，发现这可以使这个网络的学习更快。

model.add(LSTM(150, batch_input_shape=(21, 5, 100), stateful=True))
...
model.add(TimeDistributed(Dense(100, activation='softmax')))

第一个隐藏层是编码器。

我们必须添加一个额外的隐藏 LSTM 层来充当解码器。同样，我们将在此层中使用 150 个内存单元，并且与前面的示例一样，TimeDistributed 层之前的层将返回序列而不是单个值。

model.add(LSTM(150, return_sequences=True, stateful=True))

这两层不能整齐地配合在一起。编码器层将输出 2D 数组（21,150），并且解码器期望 3D 数组作为输入（21，α，150）。

我们通过在编码器和解码器之间添加 RepeatVector（）层来解决这个问题，并确保编码器的输出重复适当的次数以匹配输出序列的长度。在这种情况下，输出序列中两个时间步长为 2 次。

model.add(RepeatVector(2))

因此，LSTM 网络定义为：

model = Sequential()
model.add(LSTM(150, batch_input_shape=(21, 5, 100), stateful=True))
model.add(RepeatVector(2))
model.add(LSTM(150, return_sequences=True, stateful=True))
model.add(TimeDistributed(Dense(100, activation='softmax')))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])

训练时期的数量从 500 增加到 5,000，以说明网络的额外容量。

示例的其余部分是相同的。

将这些结合在一起，下面提供了完整的代码清单。

from random import randint
from numpy import array
from numpy import argmax
from pandas import DataFrame
from pandas import concat
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import TimeDistributed
from keras.layers import RepeatVector

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# convert encoded sequence to supervised learning
def to_supervised(sequence, n_in, n_out):
	# create lag copies of the sequence
	df = DataFrame(sequence)
	df = concat([df.shift(n_in-i-1) for i in range(n_in)], axis=1)
	# drop rows with missing values
	df.dropna(inplace=True)
	# specify columns for input and output pairs
	values = df.values
	width = sequence.shape[1]
	X = values.reshape(len(values), n_in, width)
	y = values[:, 0:(n_out*width)].reshape(len(values), n_out, width)
	return X, y

# prepare data for the LSTM
def get_data(n_in, n_out):
	# generate random sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# convert to X,y pairs
	X,y = to_supervised(encoded, n_in, n_out)
	return X,y

# define LSTM
n_in = 5
n_out = 2
encoded_length = 100
batch_size = 21
model = Sequential()
model.add(LSTM(150, batch_input_shape=(batch_size, n_in, encoded_length), stateful=True))
model.add(RepeatVector(n_out))
model.add(LSTM(150, return_sequences=True, stateful=True))
model.add(TimeDistributed(Dense(encoded_length, activation='softmax')))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
# train LSTM
for epoch in range(5000):
	# generate new random sequence
	X,y = get_data(n_in, n_out)
	# fit model for one epoch on this sequence
	model.fit(X, y, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
	model.reset_states()
# evaluate LSTM
X,y = get_data(n_in, n_out)
yhat = model.predict(X, batch_size=batch_size, verbose=0)
# decode all pairs
for i in range(len(X)):
	print('Expected:', one_hot_decode(y[i]), 'Predicted', one_hot_decode(yhat[i]))

运行该示例将显示每个训练时期随机生成的序列的日志丢失和准确率。

选择的配置意味着模型将收敛到 100％的分类准确度。

生成最终随机生成的序列，并比较预期序列与预测序列。运行示例时生成的特定序列可能不同。

...
Epoch 1/1
0s - loss: 0.0248 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0399 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0285 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0410 - acc: 0.9762
Epoch 1/1
0s - loss: 0.0236 - acc: 1.0000
Expected: [6, 52] Predicted [6, 52]
Expected: [52, 96] Predicted [52, 96]
Expected: [96, 45] Predicted [96, 45]
Expected: [45, 69] Predicted [45, 69]
Expected: [69, 52] Predicted [69, 52]
Expected: [52, 96] Predicted [52, 96]
Expected: [96, 11] Predicted [96, 96]
Expected: [11, 96] Predicted [11, 96]
Expected: [96, 54] Predicted [96, 54]
Expected: [54, 27] Predicted [54, 27]
Expected: [27, 48] Predicted [27, 48]
Expected: [48, 9] Predicted [48, 9]
Expected: [9, 32] Predicted [9, 32]
Expected: [32, 62] Predicted [32, 62]
Expected: [62, 41] Predicted [62, 41]
Expected: [41, 54] Predicted [41, 54]
Expected: [54, 20] Predicted [54, 20]
Expected: [20, 80] Predicted [20, 80]
Expected: [80, 63] Predicted [80, 63]
Expected: [63, 69] Predicted [63, 69]
Expected: [69, 36] Predicted [69, 36]

扩展

本节列出了您可能希望探索的教程的一些可能的扩展。

• 线性表示。使用了问题的分类（单热编码）框架，显着增加了模拟该问题所需的权重数量（每个随机整数 100 个）。使用线性表示（将整数缩放到 0-1 之间的值）进行探索，并将问题建模为回归。了解这将如何影响系统技能，所需的网络规模（内存单元）和训练时间（时期）。
• 掩码缺失值。当序列数据被构造为监督学习问题时，删除了具有缺失数据的行。使用屏蔽层或特殊值（例如-1）进行探索，以允许网络忽略或学习忽略这些值。
• Echo Longer Sequences 。学会回应的部分子序列只有 2 个项目。使用编解码器网络探索打印更长的序列。请注意，您可能需要更长时间（更多迭代）训练更大的隐藏层（更多内存单元）。
• 忽略状态。注意仅在每个随机整数序列的所有样品的末尾清除状态而不是在序列内洗涤样品。这可能不是必需的。使用批量大小为 1 的无状态 LSTM 探索和对比模型表现（在每个序列的每个样本之后进行重量更新和状态重置）。我希望几乎没有变化。
• 备用网络拓扑。注意使用 TimeDistributed 包装器作为输出层，以确保使用多对多网络来模拟问题。通过一对一配置（作为功能的时间步长）或多对一（作为功能向量的输出）探索序列打印问题，并了解它如何影响所需的网络大小（内存单元）和训练时间（时代）。我希望它需要更大的网络，并需要更长的时间。

你有没有探索过这些扩展？
在下面的评论中分享您的发现。

摘要

在本教程中，您了解了如何开发 LSTM 循环神经网络以从随机生成的整数列表中打印序列和部分序列。

具体来说，你学到了：

• 如何生成随机的整数序列，使用单热编码表示它们，并将问题构建为监督学习问题。
• 如何开发基于序列到序列的 LSTM 网络以打印整个输入序列。
• 如何开发基于编解码器的 LSTM 网络，以打印长度与输入序列长度不同的部分输入序列。

你有任何问题吗？
在评论中发表您的问题，我会尽力回答。

带有注意力的编解码器 RNN 架构的实现模式

原文： machinelearningmastery.com/implementation-patterns-encoder-decoder-rnn-architecture-attention/

用于循环神经网络的编解码器架构被证明在自然语言处理领域中的一系列序列到序列预测问题上是强大的。

注意力是一种解决编解码器架构在长序列上的限制的机制，并且通常加速学习并提高模型在序列到序列预测问题上的技能。

在这篇文章中，您将发现用于实现编解码器模型的模式，无论是否受到关注。

阅读这篇文章后，你会知道：

• 编解码器循环神经网络的直接与递归实现模式。
• 注意力如何适合编解码器模型的直接实现模式。
• 如何使用编解码器模型的递归实现模式来实现关注。

让我们开始吧。

具有注意力的编解码器 RNN 架构的实现模式
照片由 Philip McErlean ，保留一些权利。

注意编解码器

用于循环神经网络的编解码器模型是用于序列到序列预测问题的架构，其中输入序列的长度不同于输出序列的长度。

它由两个子模型组成，顾名思义：

• 编码器：编码器负责逐步执行输入时间步长并将整个序列编码为称为上下文向量的固定长度向量。
• 解码器：解码器负责在从上下文向量读取时逐步执行输出时间步长。

该架构的问题在于长输入或输出序列的表现差。原因被认为是由于编码器使用的固定大小的内部表示。

注意是解决此限制的架构的扩展。它的工作原理是首先提供从编码器到解码器的更丰富的上下文和学习机制，其中解码器可以在预测输出序列中的每个时间步长时学习在更丰富的编码中注意的位置。

有关编解码器架构的更多信息，请参阅帖子：

• 编解码器长短期记忆网络

直接编解码器实现

有多种方法可以将编解码器架构实现为系统。

一种方法是在给定编码器输入的情况下从解码器整体产生输出。这就是模型经常被描述的方式。

…我们提出了一种新颖的神经网络架构，它学习将可变长度序列编码成固定长度的向量表示，并将给定的固定长度向量表示解码回可变长度序列。

• 使用 RNN 编解码器进行统计机器翻译的学习短语表示，2014。

我们将此模型称为直接编解码器实现，因为缺少更好的名称。

为了清楚起见，让我们通过一个法国到英语神经机器翻译的小插图。

1. 法语的句子作为输入提供给模型。
2. 编码器一次一个字地读取该句子，并将该序列编码为固定长度的向量。
3. 解码器读取编码输入并以英语输出每个单词。

以下是此实现的描述。

神经机器翻译的直接编解码器模型实现

递归编解码器实现

另一种实现是对模型进行帧化，使得它仅生成一个字，并且递归地调用模型以生成整个输出序列。

我们将这称为递归实现（缺少更好的名称），以区别于上面的描述。

在他们关于标题为“_ 将图像放入图像标题 _
_ 发生器 ”的标题生成模型的论文中，“Marc Tanti，et al。将直接方法称为“ 连续视图 _”：

传统上，神经语言模型被描述为字符串被认为是连续生成的。在每个时间步之后生成一个新单词，RNN 的状态与最后生成的单词组合以生成下一个单词。我们将此称为“连续视图”。

• 将图像放在图像标题生成器中的位置，2017 年。

他们将递归实现称为“_ 不连续视图 _”：

我们建议根据一系列随时间的不连续快照来考虑 RNN，每个字都是从前一个字的整个前缀生成的，并且每次都重新初始化 RNN 的状态。我们将此称为“不连续视图”

— Where to put the Image in an Image Caption Generator, 2017.

我们可以使用递归实现逐步完成相同的法语 - 英语神经机器翻译示例。

1. 法语的句子作为输入提供给模型。
2. 编码器一次一个字地读取该句子，并将该序列编码为固定长度的向量。
3. 解码器读取编码输入并输出一个英文单词。
4. 输出与编码的法语句子一起作为输入，转到步骤 3。

Below is a depiction of this implementation.

神经机器翻译的递归编解码器模型实现

为了开始该过程，可能需要向模型提供“_ 序列开始 _”令牌作为到目前为止生成的输出序列的输入。

到目前为止生成的整个输出序列可以被重放作为具有或不具有编码输入序列的解码器的输入，以允许解码器在预测下一个字之前到达相同的内部状态，如果模型生成整个模型那么输出序列一次，如上一节所述。

合并编解码器实现

递归实现可以模仿输出整个序列，如在第一个模型中那样。

递归实现还允许您改变模型并寻求更简单或更熟练的模型。

一个示例是还对输入序列进行编码并使用解码器模型来学习如何最佳地组合到目前为止生成的编码输入序列和输出序列。 Marc Tanti，et al。在他们的论文中“_ 循环神经网络（RNN）在图像标题生成器中的作用是什么？_ “称之为”合并模式。“

…在给定的时间步长，合并架构通过将到目前为止生成的字符串的 RNNencoded 前缀（生成过程的“过去”）与非语言信息（生成过程的指南）组合来预测下一步生成什么。

• 循环神经网络（RNN）在图像标题生成器中的作用是什么？ ，2017

该模型仍然是递归调用的，只有模型的内部结构是变化的。我们可以用一个描述清楚地说明这一点。

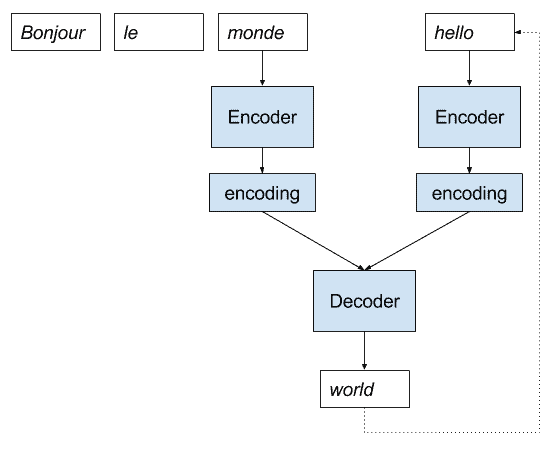
用于神经机器翻译的合并编解码器模型实现

具有注意实现的直接编解码器

我们现在可以在编解码器循环神经网络架构的这些不同实现的上下文中考虑注意机制。

正如 Bahdanau 等人所描述的那样。在他们的论文“通过联合学习对齐和翻译的神经机器翻译”，涉及以下几个要素：

• 更丰富的编码。编码器的输出被扩展，以提供输入序列中所有字的信息，而不仅仅是序列中最后一个字的最终输出。
• 对齐模型。新的小神经网络模型用于使用来自前一时间步骤的解码器的有人参与输出来对齐或关联扩展编码。
• 加权编码。对齐的加权，可用作编码输入序列上的概率分布。
• 加权上下文向量。应用于编码输入序列的加权然后可用于解码下一个字。

注意，在所有这些编解码器模型中，模型的输出（下一个预测字）和解码器的输出（内部表示）之间存在差异。解码器不直接输出字;通常，完全连接的层连接到解码器，该解码器输出单词词汇表上的概率分布，然后使用诸如集束搜索的启发式进一步搜索。

有关如何计算编解码器模型中的注意力的更多详细信息，请参阅帖子：

• 编解码器循环神经网络中的注意事项如何工作

我们可以关注直接编解码器模型的动画，如下所示。

基于注意模型的直接编解码器在神经机器翻译中的应用

在直接编解码器模型中实现注意力可能具有挑战性。这是因为具有向量化方程的有效神经网络库需要在计算之前获得所有信息。

对于每个预测，模型需要从解码器访问有人参与的输出，从而中断了这种需要。

具有注意实现的递归编解码器

注意力有助于递归描述和实现。

注意力的递归实现要求除了使得到目前为止生成的输出序列可用于解码器之外，还可以将从前一时间步骤生成的解码器的输出提供给用于预测下一个字的注意机制。

我们可以用卡通更清楚。

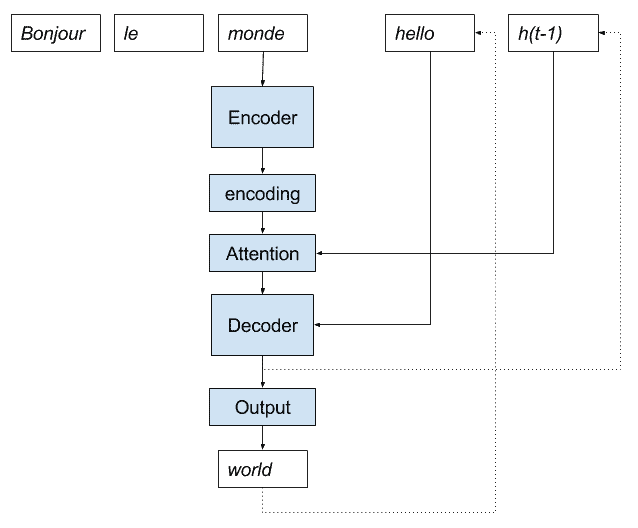
基于注意模型实现神经机器人翻译的递归编解码器

递归方法还为尝试新设计带来了额外的灵活性。

例如，Luong 等人。在他们的论文“ _ 基于注意力的神经机器翻译的有效方法 _ ”更进一步，并提出从前一时间步骤（h（t-1）解码器的输出））也可以作为输入馈送到解码器，而不是用于注意力计算。他们称之为“投入喂养”模式。

拥有这种联系的效果是双重的：（a）我们希望使模型充分了解先前的对齐选择，并且（b）我们创建一个跨越水平和垂直的非常深的网络

• 基于注意力的神经机器翻译的有效方法，2015。

有趣的是，这种输入馈送加上他们的本地关注导致了标准机器翻译任务的最新表现（在他们写作时）。

输入馈送方法与合并模型有关。合并模型不是仅提供来自上一时间步的解码输出，而是提供所有先前生成的时间步的编码。

人们可以想象在解码器中注意利用这种编码来帮助解码编码的输入序列，或者可能在两种编码上都使用注意力。

进一步阅读

如果您希望深入了解，本节将提供有关该主题的更多资源。

帖子

• 编解码器长短期记忆网络
• 长期短期记忆循环神经网络的注意事项
• 编解码器循环神经网络中的注意事项如何工作

文件

• 使用 RNN 编解码器进行统计机器翻译的学习短语表示，2014。
• 通过共同学习对齐和翻译的神经机器翻译，2015。
• 将图像放在图像标题生成器中的位置，2017。
• 循环神经网络（RNN）在图像标题生成器中的作用是什么？ ，2017
• 基于注意力的神经机器翻译的有效方法，2015。

摘要

在这篇文章中，您发现了用于实现编解码器模型的模式，无论是否受到关注。

具体来说，你学到了：

• 编解码器循环神经网络的直接与递归实现模式。
• 注意力如何适合编解码器模型的直接实现模式。
• 如何使用编解码器模型的递归实现模式来实现关注。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

学习使用编解码器 LSTM 循环神经网络相加数字

原文： machinelearningmastery.com/learn-add-numbers-seq2seq-recurrent-neural-networks/

长短期记忆（LSTM）网络是一种循环神经网络（RNN），能够学习输入序列中元素之间的关系。

LSTM 的一个很好的演示是学习如何使用诸如和的数学运算将多个项组合在一起并输出计算结果。

初学者常犯的一个错误就是简单地学习从输入词到输出词的映射函数。关于这种问题的 LSTM 的良好演示涉及学习字符的排序输入（“50 + 11”）和以字符（“61”）预测序列输出。使用序列到序列或 seq2seq（编解码器），栈式 LSTM 配置的 LSTM 可以学习这个难题。

在本教程中，您将了解如何使用 LSTM 解决添加随机生成的整数序列的问题。

完成本教程后，您将了解：

• 如何学习输入项的朴素映射函数来输出加法项。
• 如何构建添加问题（和类似问题）并适当地编码输入和输出。
• 如何使用 seq2seq 范例解决真正的序列预测添加问题。

让我们开始吧。

• 更新 Aug / 2018 ：修正了模型配置描述中的拼写错误。

如何学习使用 seq2seq 循环神经网络相加数字
照片由 Lima Pix ，保留一些权利。

教程概述

本教程分为 3 个部分;他们是：

1. 相加数字
2. 作为映射问题的添加（初学者的错误）
3. 作为 seq2seq 问题添加

环境

本教程假设安装了 SciPy，NumPy，Pandas 的 Python 2 或 Python 3 开发环境。

本教程还假设 scikit-learn 和 Keras v2.0 +与 Theano 或 TensorFlow 后端一起安装。

如果您需要有关环境的帮助，请参阅帖子：

• 如何使用 Anaconda 设置用于机器学习和深度学习的 Python 环境

相加数字

任务是，给定一系列随机选择的整数，返回那些整数的总和。

例如，给定 10 + 5，模型应输出 15。

该模型将在随机生成的示例中进行训练和测试，以便学习相加数字的一般问题，而不是记住特定情况。

作为映射问题添加

（初学者的错误）

在本节中，我们将解决问题并使用 LSTM 解决它，并说明使初学者犯错误并且不利用循环神经网络的能力是多么容易。

数据生成

让我们首先定义一个函数来生成随机整数序列及其总和作为训练和测试数据。

我们可以使用 randint（）函数生成最小值和最大值之间的随机整数，例如介于 1 和 100 之间。然后我们可以对序列求和。该过程可以重复固定次数，以创建数字输入序列对和匹配的输出求和值。

例如，此代码段将创建 100 个在 1 到 100 之间添加 2 个数字的示例：

from random import seed
from random import randint

seed(1)
X, y = list(), list()
for i in range(100):
	in_pattern = [randint(1,100) for _ in range(2)]
	out_pattern = sum(in_pattern)
	print(in_pattern, out_pattern)
	X.append(in_pattern)
	y.append(out_pattern)

运行该示例将打印每个输入 - 输出对。

...
[2, 97] 99
[97, 36] 133
[32, 35] 67
[15, 80] 95
[24, 45] 69
[38, 9] 47
[22, 21] 43

一旦我们有了模式，我们就可以将列表转换为 NumPy Arrays 并重缩放值。我们必须重缩放值以适应 LSTM 使用的激活范围。

例如：

# format as NumPy arrays
X,y = array(X), array(y)
# normalize
X = X.astype('float') / float(100 * 2)
y = y.astype('float') / float(100 * 2)

综上所述，我们可以定义函数 random_sum_pairs（），它接受指定数量的示例，每个序列中的一些整数，以及生成和返回 X，y 对数据的最大整数造型。

from random import randint
from numpy import array

# generate examples of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	# format as NumPy arrays
	X,y = array(X), array(y)
	# normalize
	X = X.astype('float') / float(largest * n_numbers)
	y = y.astype('float') / float(largest * n_numbers)
	return X, y

我们可能希望稍后反转数字的重新缩放。这将有助于将预测值与预期值进行比较，并以与原始数据相同的单位获得错误分数的概念。

下面的 invert（） 函数反转了传入的预测值和期望值的标准化。

# invert normalization
def invert(value, n_numbers, largest):
	return round(value * float(largest * n_numbers))

配置 LSTM

我们现在可以定义一个 LSTM 来模拟这个问题。

这是一个相对简单的问题，因此模型不需要非常大。输入层将需要 1 个输入功能和 2 个时间步长（在添加两个数字的情况下）。

定义了两个隐藏的 LSTM 层，第一个具有 6 个单元，第二个具有 2 个单元，接着是完全连接的输出层，其返回单个总和值。

在给定网络的实值输出的情况下，使用有效的 ADAM 优化算法来拟合模型以及均方误差损失函数。

# create LSTM
model = Sequential()
model.add(LSTM(6, input_shape=(n_numbers, 1), return_sequences=True))
model.add(LSTM(6))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')

该网络适用于 100 个时期，每个时期生成新的示例，并且在每个批次结束时执行重量更新。

# train LSTM
for _ in range(n_epoch):
	X, y = random_sum_pairs(n_examples, n_numbers, largest)
	X = X.reshape(n_examples, n_numbers, 1)
	model.fit(X, y, epochs=1, batch_size=n_batch, verbose=2)

LSTM 评估

我们在 100 个新模式上评估网络。

生成这些并且为每个预测总和值。实际和预测的和值都被重缩放到原始范围，并且计算出具有与原始值相同的比例的均方根误差（RMSE）分数。最后，列出了约 20 个预期值和预测值的示例作为示例。

最后，列出了 20 个预期值和预测值的示例作为示例。

# evaluate on some new patterns
X, y = random_sum_pairs(n_examples, n_numbers, largest)
X = X.reshape(n_examples, n_numbers, 1)
result = model.predict(X, batch_size=n_batch, verbose=0)
# calculate error
expected = [invert(x, n_numbers, largest) for x in y]
predicted = [invert(x, n_numbers, largest) for x in result[:,0]]
rmse = sqrt(mean_squared_error(expected, predicted))
print('RMSE: %f' % rmse)
# show some examples
for i in range(20):
	error = expected[i] - predicted[i]
	print('Expected=%d, Predicted=%d (err=%d)' % (expected[i], predicted[i], error))

完整的例子

我们可以将这一切联系起来。完整的代码示例如下所示。

from random import seed
from random import randint
from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from sklearn.metrics import mean_squared_error

# generate examples of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	# format as NumPy arrays
	X,y = array(X), array(y)
	# normalize
	X = X.astype('float') / float(largest * n_numbers)
	y = y.astype('float') / float(largest * n_numbers)
	return X, y

# invert normalization
def invert(value, n_numbers, largest):
	return round(value * float(largest * n_numbers))

# generate training data
seed(1)
n_examples = 100
n_numbers = 2
largest = 100
# define LSTM configuration
n_batch = 1
n_epoch = 100
# create LSTM
model = Sequential()
model.add(LSTM(10, input_shape=(n_numbers, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
# train LSTM
for _ in range(n_epoch):
	X, y = random_sum_pairs(n_examples, n_numbers, largest)
	X = X.reshape(n_examples, n_numbers, 1)
	model.fit(X, y, epochs=1, batch_size=n_batch, verbose=2)
# evaluate on some new patterns
X, y = random_sum_pairs(n_examples, n_numbers, largest)
X = X.reshape(n_examples, n_numbers, 1)
result = model.predict(X, batch_size=n_batch, verbose=0)
# calculate error
expected = [invert(x, n_numbers, largest) for x in y]
predicted = [invert(x, n_numbers, largest) for x in result[:,0]]
rmse = sqrt(mean_squared_error(expected, predicted))
print('RMSE: %f' % rmse)
# show some examples
for i in range(20):
	error = expected[i] - predicted[i]
	print('Expected=%d, Predicted=%d (err=%d)' % (expected[i], predicted[i], error))

运行该示例会在每个时期打印一些损失信息，并通过打印运行的 RMSE 和一些示例输出来完成。

结果并不完美，但很多例子都是正确预测的。

鉴于神经网络的随机性，您的具体输出可能会有所不同。

RMSE: 0.565685
Expected=110, Predicted=110 (err=0)
Expected=122, Predicted=123 (err=-1)
Expected=104, Predicted=104 (err=0)
Expected=103, Predicted=103 (err=0)
Expected=163, Predicted=163 (err=0)
Expected=100, Predicted=100 (err=0)
Expected=56, Predicted=57 (err=-1)
Expected=61, Predicted=62 (err=-1)
Expected=109, Predicted=109 (err=0)
Expected=129, Predicted=130 (err=-1)
Expected=98, Predicted=98 (err=0)
Expected=60, Predicted=61 (err=-1)
Expected=66, Predicted=67 (err=-1)
Expected=63, Predicted=63 (err=0)
Expected=84, Predicted=84 (err=0)
Expected=148, Predicted=149 (err=-1)
Expected=96, Predicted=96 (err=0)
Expected=33, Predicted=34 (err=-1)
Expected=75, Predicted=75 (err=0)
Expected=64, Predicted=64 (err=0)

初学者的错误

一切都完成了吧？

错误。

我们解决的问题有多个输入但技术上不是序列预测问题。

实际上，您可以使用多层感知机（MLP）轻松解决它。例如：

from random import seed
from random import randint
from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from sklearn.metrics import mean_squared_error

# generate examples of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	# format as NumPy arrays
	X,y = array(X), array(y)
	# normalize
	X = X.astype('float') / float(largest * n_numbers)
	y = y.astype('float') / float(largest * n_numbers)
	return X, y

# invert normalization
def invert(value, n_numbers, largest):
	return round(value * float(largest * n_numbers))

# generate training data
seed(1)
n_examples = 100
n_numbers = 2
largest = 100
# define LSTM configuration
n_batch = 2
n_epoch = 50
# create LSTM
model = Sequential()
model.add(Dense(4, input_dim=n_numbers))
model.add(Dense(2))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
# train LSTM
for _ in range(n_epoch):
	X, y = random_sum_pairs(n_examples, n_numbers, largest)
	model.fit(X, y, epochs=1, batch_size=n_batch, verbose=2)
# evaluate on some new patterns
X, y = random_sum_pairs(n_examples, n_numbers, largest)
result = model.predict(X, batch_size=n_batch, verbose=0)
# calculate error
expected = [invert(x, n_numbers, largest) for x in y]
predicted = [invert(x, n_numbers, largest) for x in result[:,0]]
rmse = sqrt(mean_squared_error(expected, predicted))
print('RMSE: %f' % rmse)
# show some examples
for i in range(20):
	error = expected[i] - predicted[i]
	print('Expected=%d, Predicted=%d (err=%d)' % (expected[i], predicted[i], error))

运行该示例可以完美地解决问题，并且可以在更少的时期内解决问题。

RMSE: 0.000000
Expected=108, Predicted=108 (err=0)
Expected=143, Predicted=143 (err=0)
Expected=109, Predicted=109 (err=0)
Expected=16, Predicted=16 (err=0)
Expected=152, Predicted=152 (err=0)
Expected=59, Predicted=59 (err=0)
Expected=95, Predicted=95 (err=0)
Expected=113, Predicted=113 (err=0)
Expected=90, Predicted=90 (err=0)
Expected=104, Predicted=104 (err=0)
Expected=123, Predicted=123 (err=0)
Expected=92, Predicted=92 (err=0)
Expected=150, Predicted=150 (err=0)
Expected=136, Predicted=136 (err=0)
Expected=130, Predicted=130 (err=0)
Expected=76, Predicted=76 (err=0)
Expected=112, Predicted=112 (err=0)
Expected=129, Predicted=129 (err=0)
Expected=171, Predicted=171 (err=0)
Expected=127, Predicted=127 (err=0)

问题是我们将这么多的域编码到问题中，它将问题从序列预测问题转变为函数映射问题。

也就是说，输入的顺序不再重要。我们可以按照我们想要的任何方式改变它，并且仍然可以解决问题。

MLP 旨在学习映射功能，并且可以轻松解决学习如何相加数字的问题。

一方面，这是一种更好的方法来解决相加数字的具体问题，因为模型更简单，结果更好。另一方面，它是反复神经网络的可怕用法。

这是一个初学者的错误，我看到在网络上的许多“LSTMs”的介绍中被​​复制了。

作为序列预测问题的添加

帧添加的另一种方法使其成为明确的序列预测问题，反过来又使其难以解决。

我们可以将添加框架作为输入和输出字符串，让模型找出字符的含义。整个添加问题可以被构造为一串字符，例如输出“62”的“12 + 50”，或者更具体地说：

• 输入：[‘1’，‘2’，‘+’，‘5’，‘0’]
• 输出：[‘6’，‘2’]

该模型不仅必须学习字符的整数性质，还要学习要执行的数学运算的性质。

注意序列现在如何重要，并且随机改组输入将创建一个与输出序列无关的无意义序列。

还要注意问题如何转换为同时具有输入和输出序列。这称为序列到序列预测问题，或称为 seq2seq 问题。

我们可以通过添加两个数字来保持简单，但我们可以看到这可以如何缩放到可变数量的术语和数学运算，可以作为模型的输入供学习和概括。

请注意，这个形式和本例的其余部分受到了 Keras 项目中添加 seq2seq 示例的启发，尽管我从零开始重新开发它。

Data Generation

seq2seq 定义问题的数据生成涉及更多。

我们将每件作为独立功能开发，以便您可以使用它们并了解它们的工作原理。在那里挂。

第一步是生成随机整数序列及其总和，如前所述，但没有归一化。我们可以把它放在一个名为 random_sum_pairs（） 的函数中，如下所示。

from random import seed
from random import randint

# generate lists of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	return X, y

seed(1)
n_samples = 1
n_numbers = 2
largest = 10
# generate pairs
X, y = random_sum_pairs(n_samples, n_numbers, largest)
print(X, y)

仅运行此函数会打印一个在 1 到 10 之间添加两个随机整数的示例。

[[3, 10]] [13]

下一步是将整数转换为字符串。输入字符串的格式为’99 +99’，输出字符串的格式为’99’。

此函数的关键是数字填充，以确保每个输入和输出序列具有相同的字符数。填充字符应与数据不同，因此模型可以学习忽略它们。在这种情况下，我们使用空格字符填充（‘’）并填充左侧的字符串，将信息保存在最右侧。

还有其他填充方法，例如单独填充每个术语。尝试一下，看看它是否会带来更好的表现。在下面的评论中报告您的结果。

填充需要我们知道最长序列可能有多长。我们可以通过获取我们可以生成的最大整数的 log10（） 和该数字的上限来轻松计算这个数，以了解每个数字需要多少个字符。我们将最大数字加 1，以确保我们期望 3 个字符而不是 2 个字符，用于圆形最大数字的情况，例如 200.我们需要添加正确数量的加号。

max_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1

在输出序列上重复类似的过程，当然没有加号。

max_length = ceil(log10(n_numbers * (largest+1)))

下面的示例添加 to_string（） 函数，并使用单个输入/输出对演示其用法。

from random import seed
from random import randint
from math import ceil
from math import log10

# generate lists of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	return X, y

# convert data to strings
def to_string(X, y, n_numbers, largest):
	max_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1
	Xstr = list()
	for pattern in X:
		strp = '+'.join([str(n) for n in pattern])
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		Xstr.append(strp)
	max_length = ceil(log10(n_numbers * (largest+1)))
	ystr = list()
	for pattern in y:
		strp = str(pattern)
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		ystr.append(strp)
	return Xstr, ystr

seed(1)
n_samples = 1
n_numbers = 2
largest = 10
# generate pairs
X, y = random_sum_pairs(n_samples, n_numbers, largest)
print(X, y)
# convert to strings
X, y = to_string(X, y, n_numbers, largest)
print(X, y)

运行此示例首先打印整数序列和相同序列的填充字符串表示。

[[3, 10]] [13]
[' 3+10'] ['13']

接下来，我们需要将字符串中的每个字符编码为整数值。毕竟我们必须处理神经网络中的数字，而不是字符。

整数编码将问题转换为分类问题，其中输出序列可以被视为具有 11 个可能值的类输出。这恰好是具有一些序数关系的整数（前 10 个类值）。

要执行此编码，我们必须定义可能出现在字符串编码中的完整符号字母，如下所示：

alphabet = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', ' ']

然后，整数编码变成了一个简单的过程，即将字符的查找表构建为整数偏移量，并逐个转换每个字符串的每个字符。

下面的示例为整数编码提供了 integer_encode（） 函数，并演示了如何使用它。

from random import seed
from random import randint
from math import ceil
from math import log10

# generate lists of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	return X, y

# convert data to strings
def to_string(X, y, n_numbers, largest):
	max_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1
	Xstr = list()
	for pattern in X:
		strp = '+'.join([str(n) for n in pattern])
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		Xstr.append(strp)
	max_length = ceil(log10(n_numbers * (largest+1)))
	ystr = list()
	for pattern in y:
		strp = str(pattern)
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		ystr.append(strp)
	return Xstr, ystr

# integer encode strings
def integer_encode(X, y, alphabet):
	char_to_int = dict((c, i) for i, c in enumerate(alphabet))
	Xenc = list()
	for pattern in X:
		integer_encoded = [char_to_int[char] for char in pattern]
		Xenc.append(integer_encoded)
	yenc = list()
	for pattern in y:
		integer_encoded = [char_to_int[char] for char in pattern]
		yenc.append(integer_encoded)
	return Xenc, yenc

seed(1)
n_samples = 1
n_numbers = 2
largest = 10
# generate pairs
X, y = random_sum_pairs(n_samples, n_numbers, largest)
print(X, y)
# convert to strings
X, y = to_string(X, y, n_numbers, largest)
print(X, y)
# integer encode
alphabet = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', ' ']
X, y = integer_encode(X, y, alphabet)
print(X, y)

运行该示例将打印每个字符串编码模式的整数编码版本。

我们可以看到空格字符（‘’）用 11 编码，三个字符（‘3’）编码为 3，依此类推。

[[3, 10]] [13]
[' 3+10'] ['13']
[[11, 3, 10, 1, 0]] [[1, 3]]

下一步是对整数编码序列进行二进制编码。

这涉及将每个整数转换为具有与字母表相同长度的二进制向量，并用 1 标记特定整数。

例如，0 整数表示’0’字符，并且将被编码为二元向量，其中 11 元素向量的第 0 个位置为 1：[1,0,0,0,0,0,0,0， 0,0,0,0]。

下面的示例为二进制编码定义了 one_hot_encode（） 函数，并演示了如何使用它。

from random import seed
from random import randint
from math import ceil
from math import log10

# generate lists of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	return X, y

# convert data to strings
def to_string(X, y, n_numbers, largest):
	max_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1
	Xstr = list()
	for pattern in X:
		strp = '+'.join([str(n) for n in pattern])
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		Xstr.append(strp)
	max_length = ceil(log10(n_numbers * (largest+1)))
	ystr = list()
	for pattern in y:
		strp = str(pattern)
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		ystr.append(strp)
	return Xstr, ystr

# integer encode strings
def integer_encode(X, y, alphabet):
	char_to_int = dict((c, i) for i, c in enumerate(alphabet))
	Xenc = list()
	for pattern in X:
		integer_encoded = [char_to_int[char] for char in pattern]
		Xenc.append(integer_encoded)
	yenc = list()
	for pattern in y:
		integer_encoded = [char_to_int[char] for char in pattern]
		yenc.append(integer_encoded)
	return Xenc, yenc

# one hot encode
def one_hot_encode(X, y, max_int):
	Xenc = list()
	for seq in X:
		pattern = list()
		for index in seq:
			vector = [0 for _ in range(max_int)]
			vector[index] = 1
			pattern.append(vector)
		Xenc.append(pattern)
	yenc = list()
	for seq in y:
		pattern = list()
		for index in seq:
			vector = [0 for _ in range(max_int)]
			vector[index] = 1
			pattern.append(vector)
		yenc.append(pattern)
	return Xenc, yenc

seed(1)
n_samples = 1
n_numbers = 2
largest = 10
# generate pairs
X, y = random_sum_pairs(n_samples, n_numbers, largest)
print(X, y)
# convert to strings
X, y = to_string(X, y, n_numbers, largest)
print(X, y)
# integer encode
alphabet = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', ' ']
X, y = integer_encode(X, y, alphabet)
print(X, y)
# one hot encode
X, y = one_hot_encode(X, y, len(alphabet))
print(X, y)

运行该示例为每个整数编码打印二进制编码序列。

我添加了一些新行，使输入和输出二进制编码更清晰。

您可以看到单个和模式变为 5 个二进制编码向量的序列，每个向量具有 11 个元素。输出或总和变为 2 个二进制编码向量的序列，每个向量再次具有 11 个元素。

[[3, 10]] [13]
[' 3+10'] ['13']
[[11, 3, 10, 1, 0]] [[1, 3]]
[[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
  [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
  [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
  [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]]
 [[[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
   [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]]]

我们可以将所有这些步骤绑定到一个名为 generate_data（） 的函数中，如下所示。

# generate an encoded dataset
def generate_data(n_samples, n_numbers, largest, alphabet):
	# generate pairs
	X, y = random_sum_pairs(n_samples, n_numbers, largest)
	# convert to strings
	X, y = to_string(X, y, n_numbers, largest)
	# integer encode
	X, y = integer_encode(X, y, alphabet)
	# one hot encode
	X, y = one_hot_encode(X, y, len(alphabet))
	# return as numpy arrays
	X, y = array(X), array(y)
	return X, y

最后，我们需要反转编码以将输出向量转换回数字，以便我们可以将预期的输出整数与预测的整数进行比较。

下面的 invert（） 功能执行此操作。关键是首先使用 argmax（） 函数将二进制编码转换回整数，然后使用整数反向映射到字母表中的字符将整数转换回字符。

# invert encoding
def invert(seq, alphabet):
	int_to_char = dict((i, c) for i, c in enumerate(alphabet))
	strings = list()
	for pattern in seq:
		string = int_to_char[argmax(pattern)]
		strings.append(string)
	return ''.join(strings)

我们现在拥有为此示例准备数据所需的一切。

注意，这些函数是为这篇文章编写的，我没有编写任何单元测试，也没有用各种输入对它们进行战斗测试。如果您发现或发现明显的错误，请在下面的评论中告诉我。

配置并调整 seq2seq LSTM 模型

我们现在可以在这个问题上使用 LSTM 模型。

我们可以认为该模型由两个关键部分组成：编码器和解码器。

首先，输入序列一次向网络显示一个编码字符。我们需要一个编码级别来学习输入序列中的步骤之间的关系，并开发这些关系的内部表示。

网络的输入（对于两个数字的情况）是一系列 5 个编码字符（每个整数 2 个，“+”一个），其中每个向量包含 11 个可能字符的 11 个特征，序列中的每个项目可能是。

编码器将使用具有 100 个单位的单个 LSTM 隐藏层。

model = Sequential()
model.add(LSTM(100, input_shape=(5, 11)))

解码器必须将输入序列的学习内部表示转换为正确的输出序列。为此，我们将使用具有 50 个单位的隐藏层 LSTM，然后是输出层。

该问题被定义为需要两个输出字符的二进制输出向量。我们将使用相同的完全连接层（Dense）来输出每个二进制向量。要两次使用同一层，我们将它包装在 TimeDistributed（）包装层中。

输出完全连接层将使用 softmax 激活函数输出[0,1]范围内的值。

model.add(LSTM(50, return_sequences=True))
model.add(TimeDistributed(Dense(11, activation='softmax')))

但是有一个问题。

我们必须将编码器连接到解码器，它们不适合。

也就是说，编码器将为 5 个向量序列中的每个输入产生 100 个输出的 2 维矩阵。解码器是 LSTM 层，其期望[样本，时间步长，特征]的 3D 输入，以便产生具有 2 个时间步长的每个具有 11 个特征的 1 个样本的解码序列。

如果您尝试将这些碎片强制在一起，则会出现如下错误：

ValueError: Input 0 is incompatible with layer lstm_2: expected ndim=3, found ndim=2

正如我们所期望的那样。

我们可以使用 RepeatVector 层来解决这个问题。该层简单地重复提供的 2D 输入 n 次以创建 3D 输出。

RepeatVector 层可以像适配器一样使用，以将网络的编码器和解码器部分组合在一起。我们可以配置 RepeatVector 重复输入 2 次。这将创建一个 3D 输出，包括两个来自编码器的序列输出副本，我们可以使用相同的完全连接层对两个所需输出向量中的每一个进行两次解码。

model.add(RepeatVector(2))

该问题被定义为 11 类的分类问题，因此我们可以优化对数损失（categorical_crossentropy）函数，甚至可以跟踪每个训练时期的准确率和损失。

把这些放在一起，我们有：

# define LSTM configuration
n_batch = 10
n_epoch = 30
# create LSTM
model = Sequential()
model.add(LSTM(100, input_shape=(n_in_seq_length, n_chars)))
model.add(RepeatVector(n_out_seq_length))
model.add(LSTM(50, return_sequences=True))
model.add(TimeDistributed(Dense(n_chars, activation='softmax')))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
# train LSTM
for i in range(n_epoch):
	X, y = generate_data(n_samples, n_numbers, largest, alphabet)
	print(i)
	model.fit(X, y, epochs=1, batch_size=n_batch)

为什么使用 RepeatVector 层？

为什么不将编码器的序列输出作为解码器的输入返回？

也就是说，每个输入序列时间步长的每个 LSTM 的一个输出而不是整个输入序列的每个 LSTM 的一个输出。

model.add(LSTM(100, input_shape=(n_in_seq_length, n_chars), return_sequences=True))

输入序列的每个步骤的输出使解码器在每个步骤访问输入序列的中间表示。这可能有用也可能没用。在输入序列的末尾提供最终 LSTM 输出可能更符合逻辑，因为它捕获有关整个输入序列的信息，准备映射到或计算输出。

此外，这不会在网络中留下任何内容来指定除输入之外的解码器的大小，为输入序列的每个时间步长提供一个输出值（5 而不是 2）。

您可以将输出重构为由空格填充的 5 个字符的序列。网络将完成比所需更多的工作，并且可能失去编解码器范例提供的一些压缩类型能力。试试看吧。

标题为“”的问题是序列到序列学习吗？ “关于 Keras GitHub 项目提供了一些你可以使用的替代表示的良好讨论。

评估 LSTM 模型

和以前一样，我们可以生成一批新的示例，并在算法适合后对其进行评估。

我们可以根据预测计算 RMSE 分数，尽管我在这里为了简单起见而将其排除在外。

# evaluate on some new patterns
X, y = generate_data(n_samples, n_numbers, largest, alphabet)
result = model.predict(X, batch_size=n_batch, verbose=0)
# calculate error
expected = [invert(x, alphabet) for x in y]
predicted = [invert(x, alphabet) for x in result]
# show some examples
for i in range(20):
	print('Expected=%s, Predicted=%s' % (expected[i], predicted[i]))

完整的例子

总而言之，下面列出了完整的示例。

from random import seed
from random import randint
from numpy import array
from math import ceil
from math import log10
from math import sqrt
from numpy import argmax
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.layers import TimeDistributed
from keras.layers import RepeatVector

# generate lists of random integers and their sum
def random_sum_pairs(n_examples, n_numbers, largest):
	X, y = list(), list()
	for i in range(n_examples):
		in_pattern = [randint(1,largest) for _ in range(n_numbers)]
		out_pattern = sum(in_pattern)
		X.append(in_pattern)
		y.append(out_pattern)
	return X, y

# convert data to strings
def to_string(X, y, n_numbers, largest):
	max_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1
	Xstr = list()
	for pattern in X:
		strp = '+'.join([str(n) for n in pattern])
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		Xstr.append(strp)
	max_length = ceil(log10(n_numbers * (largest+1)))
	ystr = list()
	for pattern in y:
		strp = str(pattern)
		strp = ''.join([' ' for _ in range(max_length-len(strp))]) + strp
		ystr.append(strp)
	return Xstr, ystr

# integer encode strings
def integer_encode(X, y, alphabet):
	char_to_int = dict((c, i) for i, c in enumerate(alphabet))
	Xenc = list()
	for pattern in X:
		integer_encoded = [char_to_int[char] for char in pattern]
		Xenc.append(integer_encoded)
	yenc = list()
	for pattern in y:
		integer_encoded = [char_to_int[char] for char in pattern]
		yenc.append(integer_encoded)
	return Xenc, yenc

# one hot encode
def one_hot_encode(X, y, max_int):
	Xenc = list()
	for seq in X:
		pattern = list()
		for index in seq:
			vector = [0 for _ in range(max_int)]
			vector[index] = 1
			pattern.append(vector)
		Xenc.append(pattern)
	yenc = list()
	for seq in y:
		pattern = list()
		for index in seq:
			vector = [0 for _ in range(max_int)]
			vector[index] = 1
			pattern.append(vector)
		yenc.append(pattern)
	return Xenc, yenc

# generate an encoded dataset
def generate_data(n_samples, n_numbers, largest, alphabet):
	# generate pairs
	X, y = random_sum_pairs(n_samples, n_numbers, largest)
	# convert to strings
	X, y = to_string(X, y, n_numbers, largest)
	# integer encode
	X, y = integer_encode(X, y, alphabet)
	# one hot encode
	X, y = one_hot_encode(X, y, len(alphabet))
	# return as numpy arrays
	X, y = array(X), array(y)
	return X, y

# invert encoding
def invert(seq, alphabet):
	int_to_char = dict((i, c) for i, c in enumerate(alphabet))
	strings = list()
	for pattern in seq:
		string = int_to_char[argmax(pattern)]
		strings.append(string)
	return ''.join(strings)

# define dataset
seed(1)
n_samples = 1000
n_numbers = 2
largest = 10
alphabet = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', ' ']
n_chars = len(alphabet)
n_in_seq_length = n_numbers * ceil(log10(largest+1)) + n_numbers - 1
n_out_seq_length = ceil(log10(n_numbers * (largest+1)))
# define LSTM configuration
n_batch = 10
n_epoch = 30
# create LSTM
model = Sequential()
model.add(LSTM(100, input_shape=(n_in_seq_length, n_chars)))
model.add(RepeatVector(n_out_seq_length))
model.add(LSTM(50, return_sequences=True))
model.add(TimeDistributed(Dense(n_chars, activation='softmax')))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
# train LSTM
for i in range(n_epoch):
	X, y = generate_data(n_samples, n_numbers, largest, alphabet)
	print(i)
	model.fit(X, y, epochs=1, batch_size=n_batch)

# evaluate on some new patterns
X, y = generate_data(n_samples, n_numbers, largest, alphabet)
result = model.predict(X, batch_size=n_batch, verbose=0)
# calculate error
expected = [invert(x, alphabet) for x in y]
predicted = [invert(x, alphabet) for x in result]
# show some examples
for i in range(20):
	print('Expected=%s, Predicted=%s' % (expected[i], predicted[i]))

运行示例几乎完全符合问题。事实上，运行更多的迭代或增加每个迭代的重量更新（ batch_size = 1 ）会让你到达那里，但需要 10 倍的时间来训练。

我们可以看到预测的结果与我们看到的前 20 个例子的预期结果相符。

...
Epoch 1/1
1000/1000 [==============================] - 2s - loss: 0.0579 - acc: 0.9940
Expected=13, Predicted=13
Expected=13, Predicted=13
Expected=13, Predicted=13
Expected= 9, Predicted= 9
Expected=11, Predicted=11
Expected=18, Predicted=18
Expected=15, Predicted=15
Expected=14, Predicted=14
Expected= 6, Predicted= 6
Expected=15, Predicted=15
Expected= 9, Predicted= 9
Expected=10, Predicted=10
Expected= 8, Predicted= 8
Expected=14, Predicted=14
Expected=14, Predicted=14
Expected=19, Predicted=19
Expected= 4, Predicted= 4
Expected=13, Predicted=13
Expected= 9, Predicted= 9
Expected=12, Predicted=12

扩展

本节列出了您可能希望探索的本教程的一些自然扩展。

• 整数编码。探索问题是否可以单独使用整数编码来更好地了解问题。大多数输入之间的序数关系可能非常有用。
• 变量号。更改示例以在每个输入序列上支持可变数量的术语。只要执行足够的填充，这应该是直截了当的。
• 可变数学运算。更改示例以改变数学运算，以允许网络进一步概括。
• 括号。允许使用括号和其他数学运算。

你尝试过这些扩展吗？
在评论中分享您的发现;我很想看到你发现了什么。

进一步阅读

本节列出了一些可供进一步阅读的资源以及您可能觉得有用的其他相关示例。

文件

• 神经网络序列学习，2014 [PDF]
• 使用 RNN 编解码器进行统计机器翻译的学习短语表示，2014 [PDF]
• LSTM 可以解决困难的长时滞问题 [PDF]
• 学会执行，2014 [PDF]

代码和帖子

• Keras 加法示例
• 烤宽面条中的加法示例
• RNN 加成（一年级）和笔记本
• 任何人都可以学习用 Python 编写 LSTM-RNN（第一部分：RNN）
• Tensorflow 中 50 行 LSTM 的简单实现

摘要

在本教程中，您了解了如何开发 LSTM 网络以了解如何使用 seq2seq 栈式 LSTM 范例将随机整数添加到一起。

具体来说，你学到了：

• 如何学习输入项的朴素映射函数来输出加法项。
• 如何构建添加问题（和类似问题）并适当地编码输入和输出。
• 如何使用 seq2seq 范例解决真正的序列预测添加问题。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

如何学习在 Keras 中用 LSTM 回显随机整数

原文：https://machinelearningmastery.com/learn-echo-random-integers-long-short-term-memory-recurrent-neural-networks/

最后更新于 2020 年 8 月 27 日

长短期记忆(LSTM)递归神经网络能够学习长序列数据中的顺序依赖性。

它们是一种基本技术，用于一系列最先进的结果，如图像字幕和机器翻译。

它们也很难理解，特别是如何设计一个问题来充分利用这种网络。

在本教程中，您将发现如何开发一个简单的 LSTM 递归神经网络，以学习如何在随机整数序列中回显数字。虽然这是一个微不足道的问题，但开发这个网络将提供将 LSTM 应用于一系列序列预测问题所需的技能。

完成本教程后，您将知道:

• 如何开发一个 LSTM，用于任何给定输入的简单回显问题。
• 如何避免初学者在将 LSTMs 应用于类似回显整数的数列问题时出现的错误？
• 如何开发一个健壮的 LSTM 来回应随机整数序列的最后观察。

用我的新书Python 的长短期记忆网络启动你的项目，包括循序渐进教程和所有示例的 Python 源代码文件。

我们开始吧。

• 2020 年 1 月更新:更新了 Keras 2.3 和 TensorFlow 2.0 的 API。

如何学习用长短期记忆递归神经网络回应随机整数
图片由弗兰克·米歇尔提供，版权所有。

概观

本教程分为 4 个部分；它们是:

1. 生成和编码随机序列
2. 回声电流观测
3. 无语境回声滞后观察(初学者错误)
4. 回声滞后观测

环境

本教程假设您安装了 Python SciPy 环境。这个例子可以使用 Python 2 或 3。

本教程假设您已经安装了 Keras v2.0 或更高版本的 TensorFlow 或 Anano 后端。本教程不需要图形处理器，所有代码都可以在中央处理器中轻松运行。

本教程还假设您已经安装了 Sklearn、Pandas、NumPy 和 Matplotlib。

如果您需要帮助来设置您的 Python 环境，请查看这篇文章:

• 如何用 Anaconda 设置机器学习和深度学习的 Python 环境

生成和编码随机序列

第一步是编写一些代码来生成整数的随机序列，并为网络编码。

生成随机序列

我们可以在 Python 中使用 randint()函数生成随机整数，该函数接受两个参数，指示从中得出值的整数范围。

在本教程中，我们将把问题定义为 0 到 99 之间有 100 个唯一值的整数值。

randint(0, 99)

我们可以将它放在一个名为 generate_sequence()的函数中，该函数将生成一个所需长度的随机整数序列，默认长度设置为 25 个元素。

下面列出了该功能。

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

一种热编码随机序列

一旦我们生成了随机整数序列，我们就需要将它们转换成适合训练 LSTM 网络的格式。

一种选择是将整数重新缩放到范围[0，1]。这是可行的，需要将问题表述为回归。

我感兴趣的是预测正确的数字，而不是接近期望值的数字。这意味着我更愿意将问题框架为分类而不是回归，其中预期输出是一个类，并且有 100 个可能的类值。

在这种情况下，我们可以使用整数值的一种热编码，其中每个值由一个 100 个元素的二进制向量表示，该向量是除了标记为 1 的整数索引之外的所有“0”值。

下面称为 one_hot_encode()的函数定义了如何迭代整数序列，并为每个整数创建二进制向量表示，并将结果作为二维数组返回。

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

我们还需要解码编码值，以便我们可以利用预测，在这种情况下，只需回顾它们。

一个热编码可以通过使用 argmax() NumPy 函数来反转，该函数返回向量中具有最大值的值的索引。

下面这个名为 one_hot_decode()的函数将对一个编码序列进行解码，并可用于以后解码来自我们网络的预测。

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

完整示例

我们可以把这一切联系起来。

下面是完整的代码清单，用于生成 25 个随机整数的序列，并将每个整数编码为二进制向量。

from random import randint
from numpy import array
from numpy import argmax

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate random sequence
sequence = generate_sequence()
print(sequence)
# one hot encode
encoded = one_hot_encode(sequence)
print(encoded)
# one hot decode
decoded = one_hot_decode(encoded)
print(decoded)

注:考虑到算法或评估程序的随机性，或数值精确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

运行该示例首先打印 25 个随机整数的列表，然后是序列中所有整数的二进制表示的截断视图，每行一个向量，然后是解码后的序列。

[37, 99, 40, 98, 44, 27, 99, 18, 52, 97, 46, 39, 60, 13, 66, 29, 26, 4, 65, 85, 29, 88, 8, 23, 61]
[[0 0 0 ..., 0 0 0]
[0 0 0 ..., 0 0 1]
[0 0 0 ..., 0 0 0]
...,
[0 0 0 ..., 0 0 0]
[0 0 0 ..., 0 0 0]
[0 0 0 ..., 0 0 0]]
[37, 99, 40, 98, 44, 27, 99, 18, 52, 97, 46, 39, 60, 13, 66, 29, 26, 4, 65, 85, 29, 88, 8, 23, 61]

现在我们知道了如何准备和表示整数的随机序列，我们可以看看如何使用 LSTMs 来学习它们。

回声电流观测

让我们从一个更简单的回声问题开始。

在本节中，我们将开发一个 LSTM 来回应当前的观察。即给定一个随机整数作为输入，返回与输出相同的整数。

或者更正式的说法是:

yhat(t) = f(X(t))

也就是说，该模型是将当前时间的值(yhat(t))预测为当前时间的观测值(X(t))的函数(f())。

这是一个简单的问题，因为不需要内存，只需要一个将输入映射到相同输出的函数。

这是一个微不足道的问题，将展示一些有用的东西:

• 如何使用上面的问题表征机制？
• 如何在 Keras 中使用 LSTMs？
• 一个 LSTM 人学习如此琐碎问题的能力。

这将为后面的滞后观测回波奠定基础。

首先，我们将开发一个函数来准备一个随机序列，准备训练或评估一个 LSTM。这个函数必须首先生成一个随机的整数序列，使用一个热编码，然后将输入数据转换成一个三维数组。

LSTMs 需要由维度[样本、时间步长、特征]组成的 3D 输入。我们的问题将由每个序列 25 个例子、1 个时间步长和一个热编码的 100 个特征组成。

下面列出了这个名为 generate_data()的函数。

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# convert to 3d for input
	X = encoded.reshape(encoded.shape[0], 1, encoded.shape[1])
	return X, encoded

接下来，我们可以定义我们的 LSTM 模型。

模型必须指定输入数据的预期维度。在这种情况下，根据时间步长(1)和特征(100)。我们将使用具有 15 个存储单元的单个隐藏层 LSTM。

输出层是一个完全连接的层(密集层)，对于可能输出的 100 个可能的整数，有 100 个神经元。输出层使用 softmax 激活函数，允许网络学习并输出可能输出值的分布。

该网络在训练时将使用对数损失函数，适用于多类分类问题，以及高效的 ADAM 优化算法。精确率度量将在每个训练时期报告，以便除了损失之外，还能了解模型的技能。

# define model
model = Sequential()
model.add(LSTM(15, input_shape=(1, 100)))
model.add(Dense(100, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

我们将通过用新生成的序列手工运行每个纪元来手动调整模型。该模型将适合 500 个时代，或者换句话说，在 500 个随机生成的序列上训练。

这将鼓励网络学习再现实际输入，而不是记忆固定的训练数据集。

# fit model
for i in range(500):
	X, y = generate_data()
	model.fit(X, y, epochs=1, batch_size=1, verbose=2)

一旦模型被拟合，我们将对一个新的序列进行预测，并将预测的输出与预期的输出进行比较。

# evaluate model on new data
X, y = generate_data()
yhat = model.predict(X)
print('Expected:  %s' % one_hot_decode(y))
print('Predicted: %s' % one_hot_decode(yhat))

下面列出了完整的示例。

from random import randint
from numpy import array
from numpy import argmax
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# convert to 3d for input
	X = encoded.reshape(encoded.shape[0], 1, encoded.shape[1])
	return X, encoded

# define model
model = Sequential()
model.add(LSTM(15, input_shape=(1, 100)))
model.add(Dense(100, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
for i in range(500):
	X, y = generate_data()
	model.fit(X, y, epochs=1, batch_size=1, verbose=2)
# evaluate model on new data
X, y = generate_data()
yhat = model.predict(X)
print('Expected:  %s' % one_hot_decode(y))
print('Predicted: %s' % one_hot_decode(yhat))

运行该示例会打印每个时期的日志丢失和准确性。

注:考虑到算法或评估程序的随机性，或数值精确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

网络有点过了，内存单元和训练时期比这么简单的问题需要的多，你可以从网络很快达到 100%的准确率这一事实看出这一点。

在运行结束时，将预测的序列与随机生成的序列进行比较，两者看起来完全相同。

...
0s - loss: 0.0895 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0785 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0789 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0832 - acc: 1.0000
Epoch 1/1
0s - loss: 0.0927 - acc: 1.0000
Expected: [18, 41, 49, 56, 86, 25, 96, 3, 75, 24, 57, 95, 81, 44, 2, 22, 76, 34, 41, 4, 69, 47, 1, 97, 57]
Predicted: [18, 41, 49, 56, 86, 25, 96, 3, 75, 24, 57, 95, 81, 44, 2, 22, 76, 34, 41, 4, 69, 47, 1, 97, 57]

既然我们知道了如何使用工具来创建和表示随机序列，以及如何拟合 LSTM 来学习呼应当前序列，那么让我们看看如何使用 LSTMs 来学习如何呼应过去的观察。

无语境回声滞后观察

( 初学者的错误)

预测滞后观测值的问题可以更正式地定义如下:

yhat(t) = f(X(t-n))

其中当前时间步长 yhat(t)的预期输出被定义为特定先前观测值(X(t-n))的函数(f())。

LSTMs 的承诺表明，你可以一次向网络展示一个例子，网络将使用内部状态来学习和充分记住先前的观察，以解决这个问题。

让我们试试这个。

首先，我们必须更新 generate_data()函数并重新定义问题。

我们将使用编码序列的移位版本作为输入，使用编码序列的截断版本作为输出，而不是使用相同的序列作为输入和输出。

这些变化是必需的，以便取一系列数字，如[1，2，3，4]，并将它们转化为具有输入(X)和输出(y)分量的监督学习问题，如:

X y
1, NaN
2, 1
3, 2
4, 3
NaN, 4

在本例中，您可以看到第一行和最后一行没有包含足够的数据供网络学习。这可能会被标记为“无数据”值并被屏蔽，但更简单的解决方案是将其从数据集中移除。

更新后的 generate_data()函数如下所示:

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# drop first value from X
	X = encoded[1:, :]
	# convert to 3d for input
	X = X.reshape(X.shape[0], 1, X.shape[1])
	# drop last value from y
	y = encoded[:-1, :]
	return X, y

我们必须测试数据的更新表示，以确认它符合我们的预期。为此，我们可以生成一个序列，并检查该序列上的解码 X 和 y 值。

X, y = generate_data()
for i in range(len(X)):
	a, b = argmax(X[i,0]), argmax(y[i])
	print(a, b)

下面提供了这种健全性检查的完整代码清单。

from random import randint
from numpy import array
from numpy import argmax
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# drop first value from X
	X = encoded[1:, :]
	# convert to 3d for input
	X = X.reshape(X.shape[0], 1, X.shape[1])
	# drop last value from y
	y = encoded[:-1, :]
	return X, y

# test data generator
X, y = generate_data()
for i in range(len(X)):
	a, b = argmax(X[i,0]), argmax(y[i])
	print(a, b)

运行该示例会打印问题框架的 X 和 y 部分。

注:考虑到算法或评估程序的随机性，或数值精确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

我们可以看到，考虑到冷启动，第一种模式对于网络来说很难(不可能)学会。我们可以通过数据看到 yhat(t)= X(t-1)的预期模式。

78 65
7 78
16 7
11 16
23 11
99 23
39 99
53 39
82 53
6 82
18 6
17 18
49 17
4 49
34 4
77 34
46 77
22 46
40 22
76 40
85 76
87 85
17 87
75 17

网络设计相似，但有一个小变化。

每次向网络显示一个观察值，并执行权重更新。因为我们期望观察之间的状态携带学习先前观察所需的信息，所以我们需要确保在每个批次之后该状态不被重置(在这种情况下，一个批次是一个训练观察)。我们可以通过使 LSTM 层有状态并在状态重置时手动管理来做到这一点。

这包括在 LSTM 图层上将有状态参数设置为真，并使用包含维度[batchsize，timesteps，features]的 batch_input_shape 参数定义输入形状。

对于给定的随机序列，有 24 个 X，y 对，因此使用 6 的批次大小(4 批次 6 个样本= 24 个样本)。请记住，序列被分解为样本，样本可以在网络权重更新之前分批显示给网络。使用 50 个内存单元的大网络大小，再次超出了解决问题所需的容量。

model.add(LSTM(50, batch_input_shape=(6, 1, 100), stateful=True))

接下来，在每个时期(随机生成的序列的一次迭代)之后，可以手动重置网络的内部状态。该模型适用于 2000 个训练时期，注意不要在一个序列中打乱样本。

# fit model
for i in range(2000):
	X, y = generate_data()
	model.fit(X, y, epochs=1, batch_size=6, verbose=2, shuffle=False)
	model.reset_states()

综上所述，下面列出了完整的示例。

from random import randint
from numpy import array
from numpy import argmax
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# drop first value from X
	X = encoded[1:, :]
	# convert to 3d for input
	X = X.reshape(X.shape[0], 1, X.shape[1])
	# drop last value from y
	y = encoded[:-1, :]
	return X, y

# define model
model = Sequential()
model.add(LSTM(50, batch_input_shape=(6, 1, 100), stateful=True))
model.add(Dense(100, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
for i in range(2000):
	X, y = generate_data()
	model.fit(X, y, epochs=1, batch_size=6, verbose=2, shuffle=False)
	model.reset_states()
# evaluate model on new data
X, y = generate_data()
yhat = model.predict(X, batch_size=6)
print('Expected:  %s' % one_hot_decode(y))
print('Predicted: %s' % one_hot_decode(yhat))

运行这个例子给出了一个令人惊讶的结果。

注:考虑到算法或评估程序的随机性，或数值精确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

该问题无法学习，训练以模型结束，该模型以 0%的精确率回应序列中的最后一个观察。

...
Epoch 1/1
0s - loss: 4.6042 - acc: 0.0417
Epoch 1/1
0s - loss: 4.6215 - acc: 0.0000e+00
Epoch 1/1
0s - loss: 4.5802 - acc: 0.0000e+00
Epoch 1/1
0s - loss: 4.6023 - acc: 0.0000e+00
Epoch 1/1
0s - loss: 4.6071 - acc: 0.0000e+00
Expected: [71, 44, 6, 11, 91, 23, 55, 37, 53, 4, 42, 15, 81, 6, 57, 97, 49, 69, 56, 86, 70, 12, 61, 48]
Predicted: [49, 49, 49, 87, 49, 96, 96, 96, 96, 96, 85, 96, 96, 96, 96, 96, 96, 96, 49, 49, 87, 96, 49, 49]

这怎么可能呢？

初学者的错误

这是初学者经常犯的错误，如果你曾经接触过 RNNs 或 LSTMs，那么你会发现上面的这个错误。

具体来说，LSTMs 的力量确实来自于所保持的习得的内部状态，但这种状态只有在被训练为过去观察的函数时才是强大的。

换句话说，您必须向网络提供预测的上下文(例如，可能包含时间相关性的观察)作为输入的时间步长。

上面的公式训练网络只学习当前输入值的输出函数，如第一个例子:

yhat(t) = f(X(t))

不是作为最后 n 次观察的函数，或者甚至只是我们要求的前一次观察:

yhat(t) = f(X(t-1))

为了学习这种未知的时间依赖性，LSTM 每次只需要一个输入，但是为了学习这种依赖性，它必须在序列上执行反向传播。您必须提供序列的过去观察作为上下文。

您没有定义窗口(如多层感知机的情况，其中每个过去的观察都是加权输入)；相反，你正在定义一个历史观测的范围，LSTM 将试图从中学习时间相关性(f(X(t-1)，… X(t-n))。

需要明确的是，这是初学者在 Keras 中使用 LSTMs 时的错误，不一定是一般的错误。

回声滞后观测

现在，我们已经绕过了初学者的一个常见陷阱，我们可以开发一个 LSTM 来重复前面的观察。

第一步是重新定义问题。

我们知道，为了做出正确的预测，网络只需要最后一次观察作为输入。但是，我们希望网络了解哪些过去的观察结果可以得到回应，以便正确解决这个问题。因此，我们将提供最后 5 个观察的子序列作为上下文。

具体来说，如果我们的序列包含:[1，2，3，4，5，6，7，8，9，10]，则 X，y 对如下所示:

X, 							y
NaN, NaN, NaN, NaN, NaN, 	NaN
NaN, NaN, NaN, NaN, 1, 		NaN
NaN, NaN, NaN, 1, 2, 		1
NaN, NaN, 1, 2, 3, 			2
NaN, 1, 2, 3, 4, 			3
1, 2, 3, 4, 5, 				4
2, 3, 4, 5, 6, 				5
3, 4, 5, 6, 7, 				6
4, 5, 6, 7, 8, 				7
5, 6, 7, 8, 9, 				8
6, 7, 8, 9, 10, 			9
7, 8, 9, 10, NaN, 			10

在这种情况下，您可以看到前 5 行和最后 1 行没有包含足够的数据，因此在这种情况下，我们将删除它们。

我们将使用 Pandas shift()函数创建序列的移位版本，使用 Pandas concat()函数将移位的序列重新组合在一起。然后，我们将手动排除不可行的行。

下面列出了更新后的 generate_data()函数。

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# create lag inputs
	df = DataFrame(encoded)
	df = concat([df.shift(4), df.shift(3), df.shift(2), df.shift(1), df], axis=1)
	# remove non-viable rows
	values = df.values
	values = values[5:,:]
	# convert to 3d for input
	X = values.reshape(len(values), 5, 100)
	# drop last value from y
	y = encoded[4:-1,:]
	print(X.shape, y.shape)
	return X, y

同样，我们可以通过生成一个序列并比较解码的 X，y 对来检查这个更新的函数。下面列出了完整的示例。

from random import randint
from numpy import array
from numpy import argmax
from pandas import concat
from pandas import DataFrame
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# create lag inputs
	df = DataFrame(encoded)
	df = concat([df.shift(4), df.shift(3), df.shift(2), df.shift(1), df], axis=1)
	# remove non-viable rows
	values = df.values
	values = values[5:,:]
	# convert to 3d for input
	X = values.reshape(len(values), 5, 100)
	# drop last value from y
	y = encoded[4:-1,:]
	return X, y

# test data generator
X, y = generate_data()
for i in range(len(X)):
	a, b, c, d, e, f = argmax(X[i,0]), argmax(X[i,1]), argmax(X[i,2]), argmax(X[i,3]), argmax(X[i,4]), argmax(y[i])
	print(a, b, c, d, e, f)

运行该示例显示最后 5 个值的上下文作为输入，最后一个先前的观察(X(t-1))作为输出。

57 96 99 77 44 77
96 99 77 44 45 44
99 77 44 45 28 45
77 44 45 28 70 28
44 45 28 70 73 70
45 28 70 73 74 73
28 70 73 74 73 74
70 73 74 73 64 73
73 74 73 64 29 64
74 73 64 29 15 29
73 64 29 15 94 15
64 29 15 94 98 94
29 15 94 98 89 98
15 94 98 89 52 89
94 98 89 52 96 52
98 89 52 96 46 96
89 52 96 46 46 46
52 96 46 46 85 46
96 46 46 85 49 85
46 46 85 49 59 49

我们现在可以开发一个 LSTM 来学习这个问题。

给定序列有 20 个 X，y 对；因此，选择批量为 5(4 批 5 个实施例= 20 个样品)。

同样的结构用于 LSTM 隐藏层的 50 个存储单元和输出层的 100 个神经元。该网络适用于 2000 个纪元，每个纪元后内部状态都会重置。

完整的代码列表如下。

from random import randint
from numpy import array
from numpy import argmax
from pandas import concat
from pandas import DataFrame
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=25):
	return [randint(0, 99) for _ in range(length)]

# one hot encode sequence
def one_hot_encode(sequence, n_unique=100):
	encoding = list()
	for value in sequence:
		vector = [0 for _ in range(n_unique)]
		vector[value] = 1
		encoding.append(vector)
	return array(encoding)

# decode a one hot encoded string
def one_hot_decode(encoded_seq):
	return [argmax(vector) for vector in encoded_seq]

# generate data for the lstm
def generate_data():
	# generate sequence
	sequence = generate_sequence()
	# one hot encode
	encoded = one_hot_encode(sequence)
	# create lag inputs
	df = DataFrame(encoded)
	df = concat([df.shift(4), df.shift(3), df.shift(2), df.shift(1), df], axis=1)
	# remove non-viable rows
	values = df.values
	values = values[5:,:]
	# convert to 3d for input
	X = values.reshape(len(values), 5, 100)
	# drop last value from y
	y = encoded[4:-1,:]
	return X, y

# define model
model = Sequential()
model.add(LSTM(50, batch_input_shape=(5, 5, 100), stateful=True))
model.add(Dense(100, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
for i in range(2000):
	X, y = generate_data()
	model.fit(X, y, epochs=1, batch_size=5, verbose=2, shuffle=False)
	model.reset_states()
# evaluate model on new data
X, y = generate_data()
yhat = model.predict(X, batch_size=5)
print('Expected:  %s' % one_hot_decode(y))
print('Predicted: %s' % one_hot_decode(yhat))

运行实例表明，该网络能够拟合问题，并正确地学习在 5 个先验观测值的背景下将 X(t-1)观测值作为预测值返回。

注:考虑到算法或评估程序的随机性，或数值精确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

输出示例如下。

...
Epoch 1/1
0s - loss: 0.1763 - acc: 1.0000
Epoch 1/1
0s - loss: 0.2393 - acc: 0.9500
Epoch 1/1
0s - loss: 0.1674 - acc: 1.0000
Epoch 1/1
0s - loss: 0.1256 - acc: 1.0000
Epoch 1/1
0s - loss: 0.1539 - acc: 1.0000
Expected: [24, 49, 86, 73, 51, 6, 6, 52, 34, 32, 0, 14, 83, 16, 37, 75, 41, 40, 80, 33]
Predicted: [24, 49, 86, 73, 51, 6, 6, 52, 34, 32, 0, 14, 83, 16, 37, 75, 41, 40, 80, 33]

扩展ˌ扩张

本节列出了本教程中实验的一些扩展。

• 忽略内部状态。通过在纪元结束时手动重置状态，注意保留序列内所有样本的 LSTMs 内部状态。我们知道，网络已经通过时间步长获得了每个样本中所需的所有上下文和状态。探索额外的交叉样本状态是否增加了模型的技能。
• 屏蔽缺失数据。在数据准备期间，删除了缺少数据的行。探索用特殊值(例如-1)标记缺失值的用法，看看 LSTM 是否可以从这些例子中学习。此外，探索如何使用掩蔽层作为输入，并探索如何掩蔽丢失的值。
• 作为时间步长的整个序列。仅提供了最后 5 个观察的上下文，作为学习呼应的上下文。探索使用整个随机序列作为每个样本的上下文，随着序列的展开而构建。这可能需要填充甚至屏蔽缺失值，以满足 LSTM 的固定大小输入的期望。
• 回声不同滞后值。在回声示例中使用了特定的滞后值(t-1)。探索在回声中使用不同的滞后值，以及这如何影响模型技能、训练时间和 LSTM 层大小等属性。我希望可以使用相同的模型结构来学习每个滞后。
• 回波滞后序列。这个网络被训练来回应一个特定的滞后观测。探索滞后序列的变化。这可能需要在网络的输出端使用时间分布层来实现顺序到顺序的预测。

你探索过这些扩展吗？
在下面的评论中分享你的发现。

摘要

在本教程中，您发现了如何开发一个 LSTM 来解决从随机整数序列中回显滞后观测值的问题。

具体来说，您了解到:

• 如何为问题生成和编码测试数据？
• 如何避免初学者在尝试用 LSTMs 解决这个和类似问题时犯的错误。
• 如何开发一个健壮的 LSTM 来回应随机整数序列中的整数。

你有什么问题吗？
在评论中提问，我会尽力回答。