不必 A/B 测试一切都是好的
实验领域的主流观点建议你测试一切。然而,一些关于 A/B 测试的不便真相表明,最好还是不要测试所有内容。
·
关注 发表在 Towards Data Science ·17 分钟阅读·2023 年 12 月 20 日
–
图片由 OpenAI 的 DALL-E 创建
在在线和产品营销领域工作的人可能听说过 A/B 测试和在线实验。近年来出现了无数的 A/B 测试平台,它们鼓励你注册并利用实验的力量来提升你的产品。许多行业领导者和小型影响者都详细讲述了 A/B 测试的成功实施及其如何改变了某些业务。我相信实验的力量吗?是的,我相信。但同时,在提高统计学水平并经历了大量的试错后,我发现,就像生活和商业中的任何事情一样,有些问题有时会被忽视,这些通常是实验中不方便的缺陷,削弱了它们作为神奇工具的地位。
为了更好地理解问题的根源,我需要从在线 A/B 测试的起源开始讲起。早期,在线 A/B 测试并不存在,但一些以创新著称的公司决定将实验转移到在线领域。当然,到那时 A/B 测试已经是科学中用来发现真相的成熟方法。这些公司包括 Google(2000 年)、Amazon(2002 年)、以及一些其他大公司如 Booking.com(2004 年),微软也很快加入。我们不难发现这些公司有一个共同点,那就是它们拥有对任何业务至关重要的两个要素:资金和资源。资源不仅仅包括基础设施,还有具备专业知识和经验的人。而且他们已经拥有了数百万的用户。顺便提一句,A/B 测试的正确实施需要上述所有条件。
直到今天,他们仍然是在线实验领域最受认可的行业声音之一,和后来出现的公司,如 Netflix、Spotify、Airbnb 等相比也不遑多让。他们的想法和方法被广泛认可和讨论,他们在在线实验中的创新也同样受到关注。他们所做的事情被认为是最佳实践,虽然不可能将所有这些内容都放入一篇小文章中,但有些内容被提及得更多,它们基本可以归纳为:
-
测试一切
-
在测试之前绝不要发布更改
-
即使是最小的变化也可能产生巨大影响
这些规则确实很有用,但并不适用于每个公司。事实上,对于许多产品和在线营销经理来说,盲目跟随这些规则可能会导致混乱甚至灾难。这是为什么呢?首先,盲目跟随任何东西都是一个坏主意,但有时我们必须依赖专家意见,因为我们在某些领域缺乏自己的专业知识和理解。我们通常忘记的是,并非所有专家意见都能很好地转化到我们自己的业务领域。这些成功的 A/B 测试基本原则的根本缺陷在于它们来源于多亿万公司,而你,读者,可能并不与其中任何一家相关联。
这篇文章将重点讨论统计功效这一已知概念及其扩展——实验的敏感性。这个概念是我在实验生活中每日决策的基础。
资源
“知识的幻觉比缺乏知识更糟” (某位聪明人)
如果你对 A/B 测试一无所知,这个想法可能看起来很简单——只需拿两个版本的东西进行比较。显示更高转化率(每用户收入、点击、注册等)的那个版本被认为更好。
如果你稍微了解一些,统计功效以及运行 A/B 测试所需样本量的计算,那么你会对检测所需效应大小的功效有所了解。如果你理解早期停止和窥探的警告——你就走在了正确的道路上。
当你进行一系列 A/A 测试时,对 A/B 测试简单性的误解会迅速被打破。在这些测试中,我们将两个完全相同的版本进行比较,并将结果展示给需要了解 A/B 测试的人。如果你有足够多的这些测试(例如 20–40 个),他们会发现有些测试显示处理组(也称为替代变体)比对照组(原始版本)有所改进,而有些测试则显示处理组实际上更差。当不断监控正在进行的实验时,我们可能会在大约 20%的时间看到显著结果。但如果我们比较的是两个相同的版本,这怎么可能呢?实际上,作者让公司的利益相关者进行了这个实验,并展示了这些误导性的结果,其中一位利益相关者回复说,这无疑是一个“错误”,如果一切设置得当,我们不会看到这样的情况。
这只是冰山一角,如果你已有一些经验,你会知道:
-
实验远非简单
-
测试不同的事物和不同的指标需要远超普通传统 A/B 测试的方法。一旦超出了简单的转化率测试,事情会变得成倍困难。你会开始关心方差及其减少,估计新奇效应和首因效应,评估分布的正态性等等。实际上,即使你知道如何处理问题,你也无法正确测试某些事物(稍后会详细说明)。
-
你可能需要一位合格的数据科学家/统计学家。实际上,你肯定需要不止一位他们,以确定在你的具体情况下应该使用什么方法,以及需要考虑哪些注意事项。这包括确定要测试什么以及如何进行测试。
-
你还需要一个合适的数据基础设施来收集分析数据并执行 A/B 测试。你选择的 A/B 测试平台的 JavaScript 库,最简单的解决方案,并不是最佳选择,因为它与已知的闪烁问题和增加的页面加载时间相关联。
-
如果不完全理解背景和在各个方面偷工减料,很容易得到误导性结果。
以下是一个简化的流程图,说明了设置和分析实验过程中涉及的决策过程。实际上,事情变得更加复杂,因为我们必须处理不同的假设,如同质性、观察独立性、正态性等。如果你已经在这个领域待了一段时间,这些词汇你是熟悉的,你知道考虑所有因素可能有多么困难。如果你对实验还不熟悉,这些词汇对你来说可能毫无意义,但希望它们能暗示你,也许事情并不像看起来那么简单。
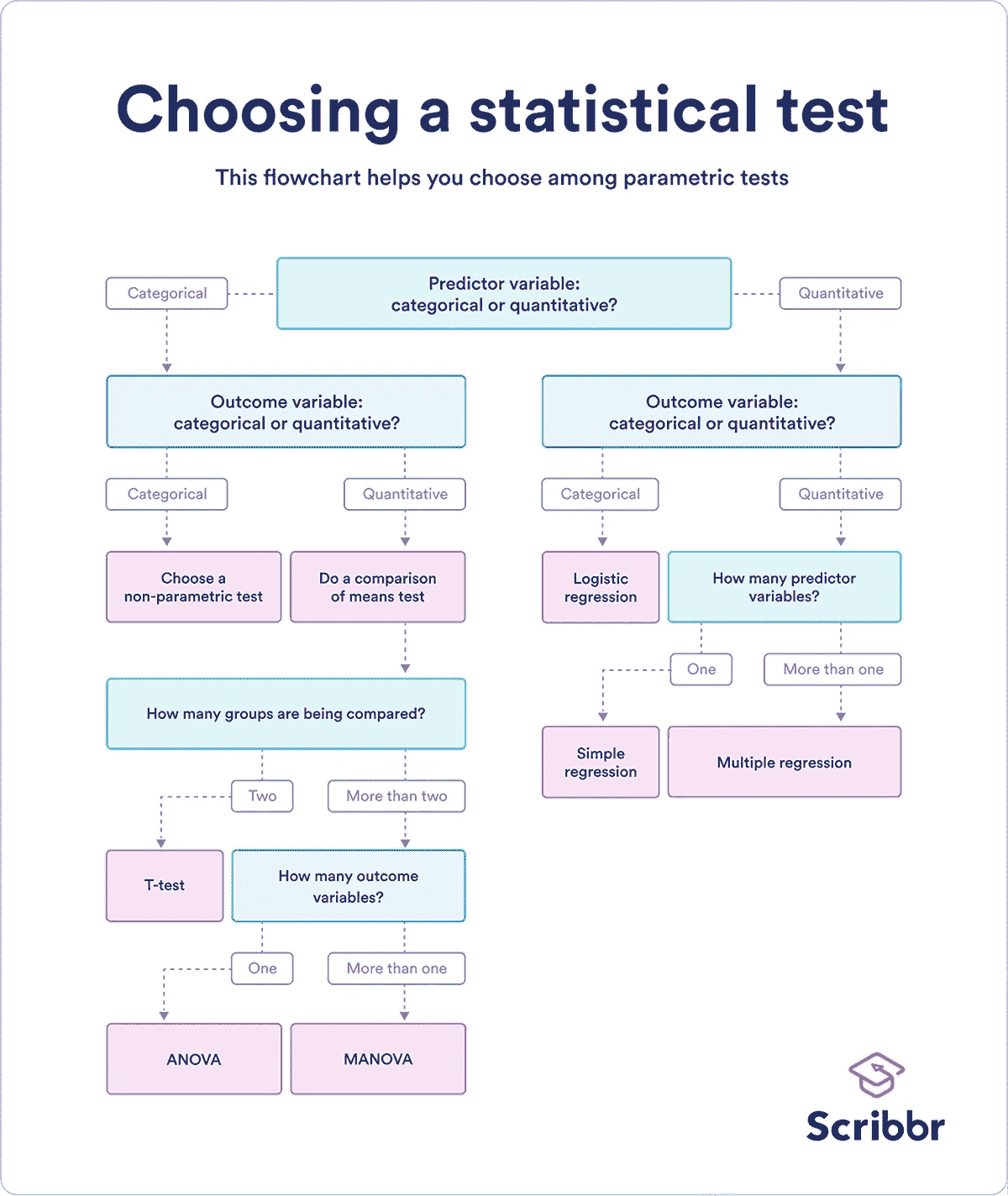
图片由Scribbr提供,已获许可
中小型公司可能会在分配设置适当 A/B 测试环境所需资源时遇到困难,每次启动 A/B 测试可能是一个耗时的任务。但这只是问题的一部分。希望在本文结束时,你能理解为什么在所有这些情况下,当经理给我发消息说“我们需要测试这个”时,我经常会回复“我们可以吗?”。真的,为什么我们不能?
用户和敏感性
在像微软和 Airbnb 这样的公司,成功实验的多数提升幅度低于 3%
那些熟悉统计功效概念的人知道,每组中的随机化单位(为简化起见,我们称之为“用户”)越多,你能够检测变体之间差异的机会就越高(其他条件相同),这也是像 Google 这样的巨大公司和你们这些普通在线业务之间的另一个关键区别——你的业务可能没有足够多的用户和流量来检测高达 3%的小差异,即使是检测 5%的提升,拥有足够统计功效(行业标准为 0.80)也是一种挑战。

在 alpha 0.05、功效 0.80、基准均值 10 和标准差 40、方差相等的情况下,不同样本大小的可检测提升。(作者提供的图片)
在上述敏感性分析中,我们可以看到,检测大约 7%的提升相对容易,只需每个变体 50000 名用户,但如果我们想要检测 3%的提升,则需要大约 275000 名用户每个变体。
温馨提示:G*Power是一个非常方便的软件,用于进行功效分析和各种功效计算,包括测试两个独立均值之间的差异的敏感性。尽管它以Cohen’s d的形式显示效应大小,但转换为提升是直接的。
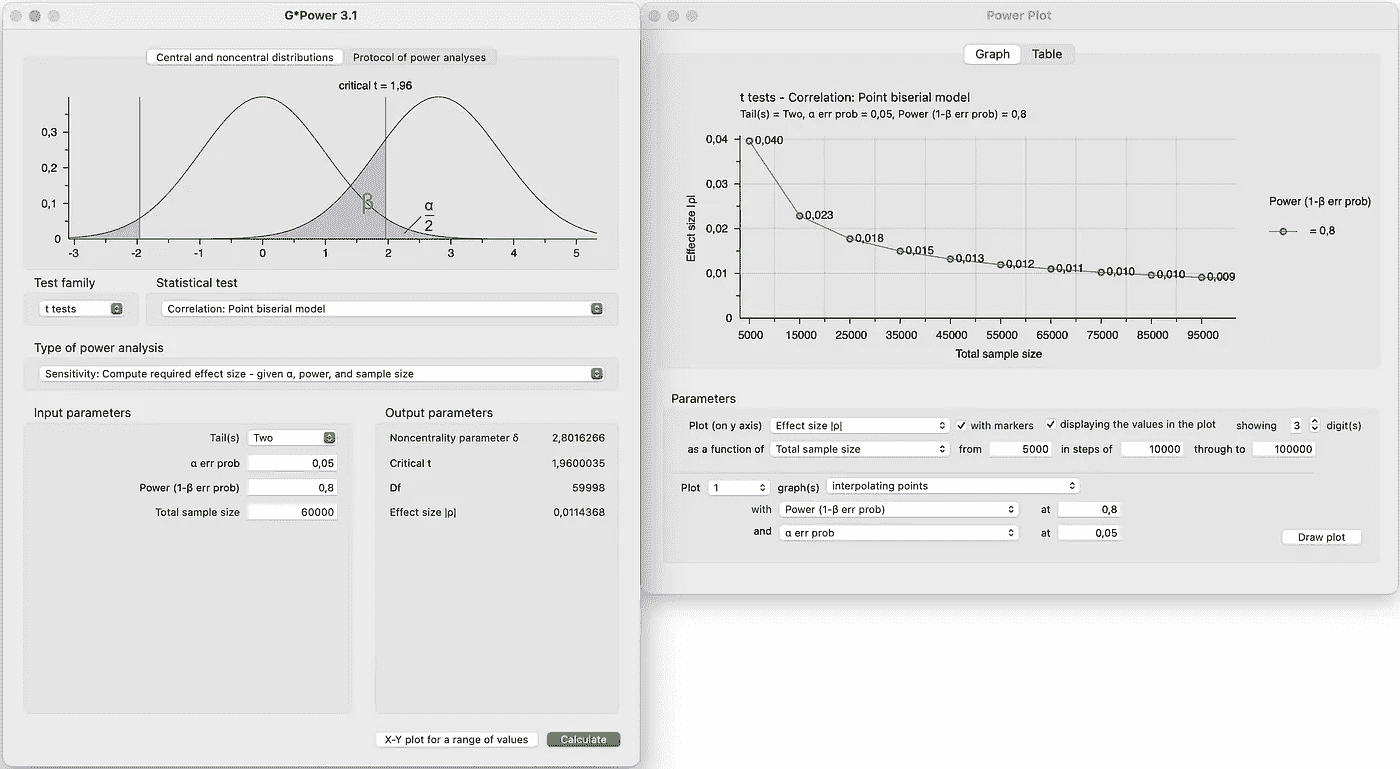
在 G*Power 中执行的测试敏感性计算的屏幕截图。(作者提供的图片)
有了这些知识,我们可以采取两条路线:
-
我们可以提出一个可接受的实验持续时间,计算 MDE,启动实验,如果未检测到差异,我们放弃更改,并假设如果存在差异,它不会高于 0.99 功效和给定显著性水平(0.05)的 MDE。
-
我们可以决定实验的持续时间,计算 MDE,如果 MDE 对于给定的持续时间太高,我们可以选择不启动实验或在不测试的情况下发布更改(第二种选项是我通常的做法)。
事实上,第一种方法在 LinkedIn 上由 Ronny Kohavi提到过:

第一种方法的缺点,尤其是对于资源有限的初创企业或小型企业,是你不断将资源投入到几乎没有机会提供可操作数据的领域。
进行不够敏感的实验可能导致参与实验的团队成员疲劳和士气低落
因此,如果你决定追求那个“圣杯”并测试所有推向生产的内容,你最终会得到的是:
-
设计师花费数天,有时数周,设计改进版本的着陆页或产品部分
-
开发人员通过你的 A/B 测试基础设施实施更改,这也需要时间
-
数据分析师和数据工程师设置额外的数据跟踪(实验所需的额外指标和分段)
-
QA 团队测试最终结果(如果你足够幸运,一切正常,无需重新修改)
-
测试被推送到生产环境中,在那里保持活动状态一到两个月
-
你和相关利益方未能检测到显著差异(除非你运行实验的时间过长,从而危及其有效性)。
在经历了一系列这样的测试之后,包括公司的顶级增长声音在内的每个人都会失去动力,并因花费如此多的时间和精力进行测试而感到沮丧,最终却得出“变体之间没有差异”的结论。但在这里,措辞扮演了至关重要的角色。请看这里:
-
变体之间没有显著差异
-
我们未能检测到变体之间的差异。如果差异为 30%或更高,我们很可能(0.99)会检测到,如果差异为 20%或更高,则概率稍低(0.80)。
第二种措辞稍微复杂一些,但信息量更多。0.99 和 0.80 是不同的统计功效水平。
-
这更符合已知的实验声明:“证据的缺乏并不是缺乏证据”。
-
这揭示了我们的实验最初有多敏感,并可能暴露公司经常遇到的问题——进行充分实验的流量有限。
加上 Ronny Kohavi 在其白皮书中提供的知识,他声称他工作过的公司中大多数实验的提升不到 3%,这让我们感到困惑。实际上,他在其出版物中建议将 MDE 保持在 5%。
我在微软、Airbnb 和亚马逊见过成千上万的实验,极少看到关键指标的提升超过 10%。[source]
我推荐的大多数电子商务网站的默认 MDE 是 5%。[source]
在必应,每月的改进
多次实验的收入通常在个位数范围内。[source, section 4]
我仍然认为,对于那些产品优化不足且仅从 A/B 测试开始的小公司来说,可能会有更高的提升,但我觉得大多数情况下不会接近 30%。
问题
在制定 A/B 测试策略时,你需要从更大的角度来看待:可用资源、流量数量以及你手头的时间。
所以,我们最终得到的结果,以及我所说的“我们”指的是那些刚开始实验之旅的相当多的企业,就是大量资源用于设计、开发测试变体,资源用于设置测试本身(包括设置指标、细分等)——所有这些加起来实际上很难在合理的时间内检测到任何东西。我可能应该再强调一下,不应该过于相信平均测试的真实效果会有 30%的提升。
我经历过这个过程,我们在 SendPulse 尝试启动实验时有过许多失败的尝试,这些尝试总是显得徒劳,直到不久前,我意识到应该跳出 A/B 测试,看到更大的图景,而更大的图景就是这样。
-
你拥有有限的资源
-
你拥有有限的流量和用户
-
你不会总是拥有进行适当实验的条件,事实上,如果你是一个较小的企业,这些条件会更为稀少。
-
你应该在自己公司的背景下计划实验,仔细分配资源,并且要合理,避免将资源浪费在徒劳的任务上
-
不对下一个变更进行实验是可以的,虽然不是理想的做法——企业在在线实验成为一种手段之前早已取得成功。你的一些变更会产生负面影响,一些则会产生积极影响,但只要积极影响大于负面影响,这也是可以接受的。
-
如果你不小心,并且对实验作为唯一真实的方法过于热衷,你可能会把大部分资源投入到一个徒劳的任务中,使公司处于不利的位置。
以下是一个被称为“证据层级”的图示。虽然个人观点位于金字塔的底部,但它仍然有一定的参考价值,但更好的做法是接受这样的事实:有时这是唯一合理的选项,尽管它有缺陷。随机实验当然在金字塔的层级中更高。
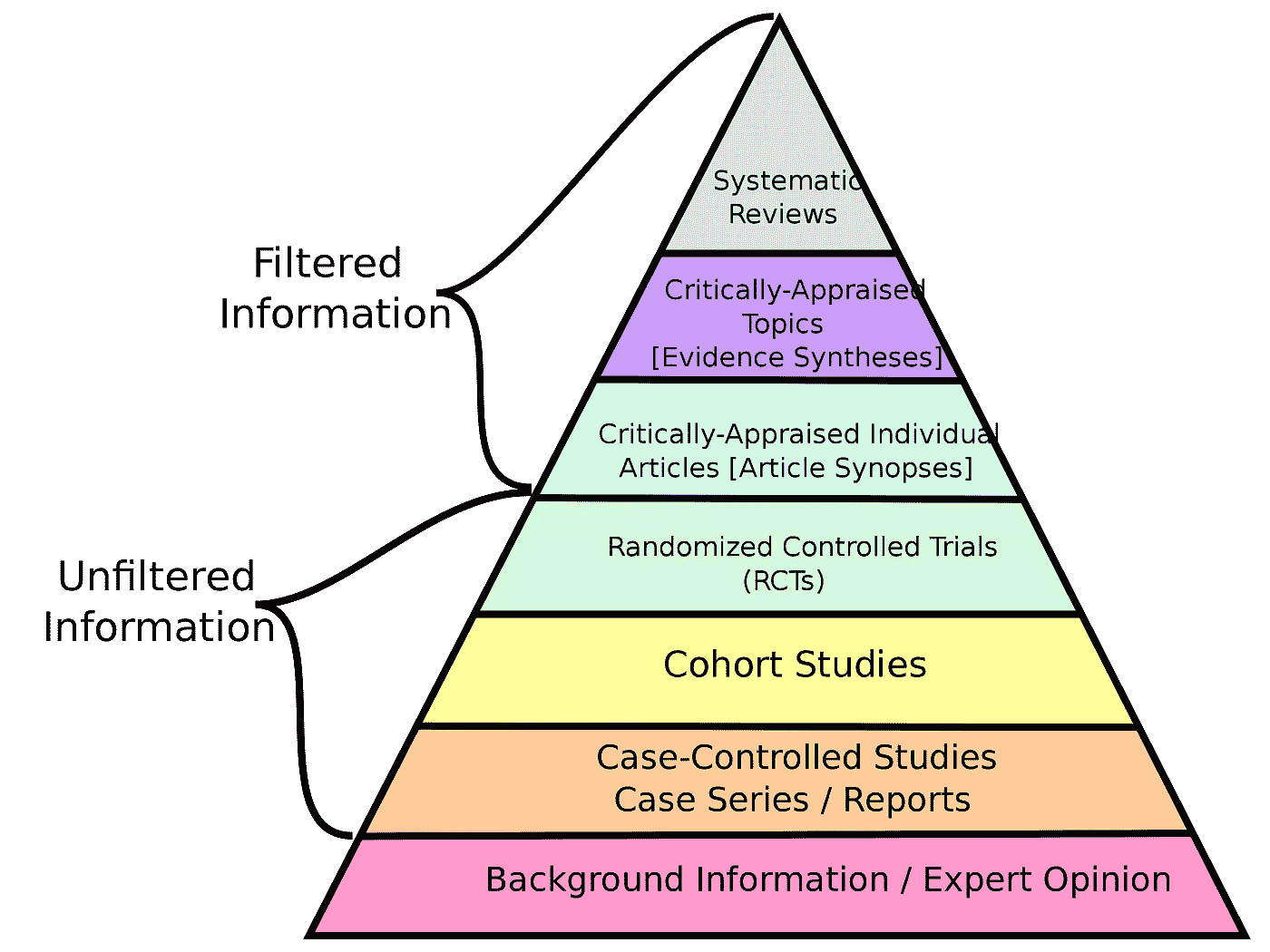
科学中的证据层级。(图片由 CFCF 提供,通过 Wikimedia Commons,按 CC BY-SA 4.0 许可证授权)
解决方案
在更传统的设置中,启动 A/B 测试的流程大致如下:
-
有人提出了某项变更的想法
-
你估算实施变更所需的资源
-
涉及到的人使变革成为现实(设计师、开发人员、产品经理)
-
你设置最小可检测效应(MDE)和其他参数(alpha、beta、测试类型——双尾、单尾)
-
你计算所需的样本量,并根据参数确定测试需要运行多久
-
你启动测试
如上所述,这种方法是“实验优先”设计的核心——实验优先,无论代价如何,所需资源将被分配。完成实验所需的时间也不是问题。但如果你发现实施改变需要两周和三个人,而实验需要运行 8 到 12 个月才能敏感足够,你会怎么想?记住,利益相关者并不总是理解 A/B 测试的敏感性概念,因此为其持续一年进行合理化可能是一个挑战,而且世界变化迅速,这可能无法接受。更不用说技术问题会妨碍测试有效性,过期的 cookies 就是其中之一。
在资源、用户和时间有限的条件下,我们可以反转流程,将其改为“资源优先”设计,这可能在你的情况下是一个合理的解决方案。
假设:
-
基于伪用户 ID(基于 cookies,这些 cookies 有时会过期和被删除)的 A/B 测试在较短的运行时间内更稳定,所以我们将其设置为最长 45 天。
-
基于稳定标识符如 user-id 的 A/B 测试可以承受更长的运行时间(例如,基于转化指标为 3 个月,基于收入指标为 5 个月)。
我们接下来要做的是:
-
查看我们在 45 天内为每个变体能收集多少单位,假设每个变体 30,000 个访问者。
-
计算在可用样本量、alpha、功效和基础转化率下你的 A/B 测试的敏感性。
-
如果效果足够合理(1%到 10%的提升),你可以考虑分配所需资源来实施改变和设置测试。
-
如果效果高于 10%,特别是高于 20%,分配资源可能不是明智的决定,因为你改变后的实际提升可能会更低,而且你也无法可靠地检测到它。
我应该注意,最大实验长度和效果阈值由你决定,但我发现这些对我们来说效果很好。
-
网站上 A/B 测试的最长时间为 45 天。
-
基于产品中转化指标和持久标识符(如 user_id)的 A/B 测试最长时间为 60 天。
-
基于产品收入指标的 A/B 测试的最长时间为 120 天。
决策的敏感性阈值:
-
高达 5%——完美,启动是完全合理的,我们可以在这方面分配更多资源。
-
5%-10%——不错,我们可以启动它,但我们应该小心投入多少资源。
-
10%-15%——可接受,如果我们不需要花费太多资源——有限的开发时间、有限的设计时间、设置额外的指标和测试的细分不多,可以启动它。
-
15%-20%——勉强可接受,但如果你需要更少的资源,并且你对成功有强烈的信念,启动可能是合理的。然而,你可能需要告知团队测试的敏感性较差。
-
20% — 不可接受。进行如此低敏感性的测试仅在少数情况下是合理的,考虑一下你可以改变实验设计的哪些方面以提高敏感性(例如,可能将更改实施在多个着陆页而不是一个上,等等)。

基于敏感性的实验分类(图像由作者提供)
注意,在我的业务环境中,我们允许基于收入的实验运行更长时间,因为:
-
收入增加是最高优先级
-
基于收入的指标具有更高的方差,因此相比于转化率指标,敏感性较低,其他条件相同
一段时间后,我们对哪些测试足够敏感有了了解:
-
跨整个网站或一组页面的更改(而不是单个页面)
-
“折叠线”上的更改(即着陆页的第一个屏幕上的更改)
-
服务中的入门流程更改(因为这是用户旅程的开始,此处用户数量达到最大值)
-
我们主要在新用户身上进行实验,忽略旧用户(以免处理可能的首因效应和新奇效应)。
更改的来源
我还应该介绍“更改的来源”这一术语,以进一步扩展我的思想和方法论。在 SendPulse,与其他公司一样,产品持续推向生产环境,包括涉及用户界面、可用性和其他外观的更改。这些更改在我们引入实验之前就已经发布了,因为,商业不能停滞不前。同时,还有一些我们特别希望测试的更改,例如有人提出了一个有趣但有风险的想法,我们不会在没有测试的情况下发布。
-
在第一种情况下,无论如何都要分配资源,并且坚信必须实施更改。这意味着我们花费在测试上的资源只是为了设置测试本身,而不是开发/设计更改,我们称之为“自然更改”。
-
在第二种情况下,所有用于测试的资源包括设计、开发更改和设置实验,我们称之为“实验性更改”。
为什么要进行这种分类?记住,我描述的哲学是从敏感性和资源的角度测试那些值得测试的内容,而不对公司现有流程造成太大干扰。我们不想让所有事情都依赖于实验,直到业务准备好为止。考虑到我们迄今所涵盖的一切,将实验逐步融入团队和公司的生活是有意义的。
上述分类允许我们在处理“自然更改”时使用以下方法:
-
如果我们考虑测试“自然变化”,我们只看设置测试需要多少资源,即使敏感度超过 20%,但所需资源最小,我们也会进行测试。
-
如果我们在指标上没有看到下降,我们坚持新的变体并将其推广到所有用户(记住,我们计划在决定测试之前就要发布它)。
-
因此,即使测试不够敏感以检测变化,我们也只是为自己设定了一个“护栏”——以防变化真的大幅度下降了指标。我们不会通过寻找确凿证据来阻止推广变化——这只是一个预防措施。
另一方面,在处理“实验性变化”时,协议可能有所不同:
-
我们需要基于“敏感度”来做决策,这在这里起着关键作用,因为我们要考虑分配多少资源来实施变化和测试本身,只有在我们有很好的机会检测到效果时,才应承诺进行工作。
-
如果我们在指标上看不到提升,我们倾向于放弃变化并保留原始版本,因此,资源可能会浪费在后续会被舍弃的东西上——这些资源应该得到仔细管理。
结果(希望是积极的)
这种策略如何帮助一个成长中的企业适应实验心态?我觉得读者此时应该已经明白,但回顾一下也没坏处。
-
你通过逐步引入 A/B 测试,给团队时间适应实验。
-
你不会将有限的资源用于那些没有足够敏感度的实验,而资源对于成长中的初创公司来说是一个问题——你可能需要将它们用于其他地方。
-
因此,你不会通过不断催促你的团队进行从未达到统计显著性的实验来迫使拒绝 A/B 测试,即使在启动它们时花费了大量时间——当你的大部分测试显示出显著的东西时,你会意识到这些努力并非徒劳。
-
通过测试“自然变化”,即团队认为应该推出的即使没有实验的东西,只有在它们显示出统计学上显著下降时才拒绝,这样你不会造成太大干扰,但如果测试确实显示出下降,你会播下怀疑的种子,表明我们的决策并非全都完美。
重要的是要记住——A/B 测试并非微不足道,它们需要巨大的努力和资源来做到正确。像世界上的任何事物一样,我们应该了解自己的极限和在特定时间的能力。仅仅因为我们想攀登珠穆朗玛峰,并不意味着我们应该在不了解自己极限的情况下去做——有很多创业公司的尸体在比喻的珠穆朗玛峰上,他们超出了自己的能力范围。
祝你实验顺利!
并非全是彩虹和阳光:ChatGPT 的阴暗面
第一部分:大型语言模型的风险和伦理问题
·
关注 发表在 Towards Data Science · 9 分钟阅读 · 2023 年 1 月 27 日
–
图片 由 Fiddler AI 提供,已获许可
如果你还没听说过 ChatGPT,你一定是躲在一块非常大的石头下。这款病毒式聊天机器人被用于自然语言处理任务,如文本生成,已经引起了广泛关注。其背后的公司 OpenAI 最近在谈判以获得 290 亿美元的估值¹,微软可能很快会再投资 100 亿美元²。
ChatGPT 是一个自回归语言模型,使用深度学习生成文本。它通过在各种领域提供详细的回答让用户感到惊讶。它的回答非常有说服力,以至于很难判断这些回答是否由人类撰写。ChatGPT 建立在 OpenAI 的 GPT-3 系列大型语言模型(LLMs)基础上,于 2022 年 11 月 30 日推出。它是最大的 LLM 之一,可以写出优美的文章和诗歌,生成可用的代码,以及根据文本描述生成图表和网站,所有这些都不需要或几乎不需要监督。ChatGPT 的回答如此出色,它显示出有可能成为无处不在的 Google 搜索引擎的潜在对手。
大型语言模型是……嗯……庞大的。它们在大量的文本数据上进行训练,这些数据可以达到 PB 级,并且具有数十亿个参数。最终的多层神经网络通常有几个 TB 大。围绕 ChatGPT 和其他 LLM 的炒作和媒体关注是可以理解的——它们确实是人类智慧的杰出成果,有时会以新兴行为让这些模型的开发者感到惊讶。例如,通过在提示的开头使用某些“魔法”短语,如“让我们一步一步思考”,可以改善 GPT-3 的回答。这些新兴行为表明了模型的巨大复杂性以及当前的可解释性缺失,甚至让开发者思考这些模型是否具有意识。
大型语言模型的幽灵
尽管有许多积极的宣传和炒作,但负责任的人工智能社区中的一些人发出了强烈的警告。值得注意的是,在 2021 年,负责人工智能领域的著名研究员 Timit Gebru 发表了一篇论文,警告了与 LLM 相关的许多伦理问题,这也导致她被谷歌解雇。这些警告涉及广泛的问题:缺乏可解释性、抄袭、隐私、偏见、模型鲁棒性以及其环境影响。让我们稍微探讨一下这些话题。
信任与缺乏可解释性:
深度学习模型,尤其是 LLM,已经变得如此庞大和不透明,以至于即使是模型的开发者也常常无法理解为什么他们的模型会做出某些预测。这种缺乏可解释性是一个重大问题,特别是在用户希望了解模型生成特定输出的原因和方式的情况下。
在轻松的风格下,我们的首席执行官 Krishna Gade 使用了 ChatGPT 创作了一首关于可解释人工智能的诗歌,风格模仿了约翰·济慈,坦率地说,我认为效果相当不错。

克里希纳正确指出,关于模型如何得出输出的透明度不足。对于 LLMs 生成的作品,缺乏关于输出所依赖数据来源的透明度意味着 ChatGPT 提供的答案无法被正确引用,因此用户无法验证或信任其输出⁹。这导致 ChatGPT 创建的答案在像 Stack Overflow¹⁰这样的论坛上被禁止。
当使用像 OpenAI 的嵌入模型¹¹这样的工具时,透明度和理解模型如何得出输出变得尤为重要,因为这些模型本质上包含了一层模糊性,或者在模型用于高风险决策的情况下。例如,如果有人使用 ChatGPT 获取急救指示,用户需要知道回应是可靠的、准确的,并且来源可信。虽然存在各种事后方法来解释模型的选择,但这些解释在模型部署时往往被忽视。
这种缺乏透明度和可信度的后果在假新闻和虚假信息泛滥的时代尤其令人担忧,因为 LLMs 可能会被微调以传播虚假信息并威胁政治稳定。虽然 Open AI 正在研究各种方法来识别其模型的输出,并计划嵌入加密标签以对输出进行水印¹²,这些负责任的 AI 解决方案的速度仍然不足,可能也不够充分。
这引发了关于……的问题。
剽窃:
精心制作的 ChatGPT 文章的来源难以追踪自然引发了关于剽窃的讨论。但这是否真的是个问题?作者认为不是。在 ChatGPT 出现之前,学生们已经可以利用写作服务¹³,且一直有少数学生决心作弊。但对 ChatGPT 使所有孩子变成无脑的剽窃者的担忧已成为许多教育者的关注重点,并导致一些学区禁止使用 ChatGPT¹⁴。
关于剽窃的讨论掩盖了与 LLMs 相关的更大、更重要的伦理问题。鉴于这一话题的广泛关注,我不得不提及它。
隐私:
如果大型语言模型用于处理敏感数据,则面临数据隐私泄露的风险。训练集来源于各种数据,有时包括个人身份信息¹⁵ — 姓名、电子邮件地址¹⁶、电话号码、地址、医疗信息 — 因此,可能会出现在模型的输出中。虽然这是任何使用敏感数据训练的模型都会面临的问题,但考虑到 LLMs 的训练集规模庞大,这个问题可能影响到很多人。
潜在偏见:
如前所述,这些模型在大量的数据语料库上进行训练。当数据训练集如此庞大时,它们变得非常难以审计,因此固有地存在风险⁵。这个数据包含社会和历史偏见¹⁷,因此任何在这些数据上训练的模型都可能会再现这些偏见,除非采取适当的保护措施。许多流行的语言模型被发现含有偏见,这可能导致偏见思想的传播增加,并对某些群体造成持续伤害。GPT-3 被发现表现出常见的性别刻板印象¹⁸,将女性与家庭和外貌联系起来,并将她们描述为比男性角色更没有权力。令人遗憾的是,它还将穆斯林与暴力联系在一起¹⁹,其中三分之二对包含“穆斯林”一词的提示的回应中都包含了暴力的参考。很可能存在更多的偏见关联尚未被发现。
值得注意的是,微软的聊天机器人在 2016 年迅速变成了最糟糕的网络恶搞者的模仿者²⁰,吐露种族主义、性别歧视和其他辱骂性语言。尽管 ChatGPT 设有过滤器以尝试避免最糟糕的此类语言,但它可能并非万无一失。OpenAI 为人工标注员支付费用,以标记最具攻击性和令人不安的数据,但其合作公司因每小时仅支付 2 美元而受到批评,工人报告称遭受了深刻的心理伤害²¹。
模型的鲁棒性和安全性:
由于大语言模型(LLMs)是预先训练的,并随后根据特定任务进行微调,这会导致一系列问题和安全风险。值得注意的是,LLMs 缺乏提供不确定性估计的能力²²。没有了解模型的置信度(或不确定性),我们很难判断何时可以信任模型的输出,何时需要保持怀疑态度²³。这影响了它们在微调到新任务时的表现以及避免过拟合的能力。可解释的不确定性估计有潜力提高模型预测的鲁棒性。
模型安全性是一个迫在眉睫的问题,原因在于 LLM 的父模型在微调步骤之前的普遍性。因此,模型可能成为单点故障和攻击的主要目标,这会影响从原始模型派生的任何应用。此外,由于缺乏监督训练,LLMs 可能会受到数据投毒的威胁²⁵,这可能导致恶意言论被注入以针对特定公司、群体或个人。
LLM 的训练语料库是通过爬取互联网上各种语言和主题来源创建的,然而它们仅仅反映了最有可能接触并频繁使用互联网的人群。因此,AI 生成的语言趋于同质化,并且通常反映了最富有的社区和国家的实践⁶。对于不在训练数据中的语言,LLMs 更容易失败,需要更多的研究来解决与分布外数据相关的问题。
环境影响与可持续性:
一篇由 Strubell 和合作者于 2019 年发表的论文概述了 LLM 训练生命周期的巨大碳足迹²⁴ ²⁶,其中,训练一个拥有 2.13 亿参数的神经架构搜索模型被估算产生的碳排放量是普通汽车生命周期排放量的五倍以上。考虑到 GPT-3 拥有 175 亿 个参数,而下一代 GPT-4 传闻拥有 100 万亿 个参数,这在面临气候变化带来的日益严重的恐怖和破坏的世界中是一个重要的方面。
现在怎么办?
任何新技术都会带来优势和劣势。我已经概述了许多与大语言模型(LLMs)相关的问题,但我想强调的是,我也对这些模型为我们每个人带来的新可能性和承诺感到兴奋。社会有责任采取适当的保障措施,并明智地使用这项新技术。任何在公众中使用或公开的模型都需要进行监控、解释,并定期审计模型的偏差。在第二部分中,我将概述对 AI/ML 从业者、企业和政府机构的建议,说明如何解决特定于 LLMs 的一些问题。
参考文献:
-
ChatGPT 创始人与投资者谈论以 290 亿美元估值出售股份,华尔街日报,2023 年。
-
Todd Bishop, 微软计划通过潜在的 100 亿美元投资和新的整合来巩固与 OpenAI 的关系,GeekWire,2023 年。
-
Parmy Olson, ChatGPT 应该让 Google 和 Alphabet 感到担忧。为什么要搜索,当你可以问 AI?,彭博社,2022 年。
-
Subbarao Kambhampati, 改变人工智能研究的性质,ACM 通信,2022 年。
-
Roger Montti, 什么是 Google LaMDA,为什么有人相信它具有意识?,搜索引擎期刊,2022 年。
-
艾米莉·M·本德,蒂姆尼特·戈布鲁,安吉丽娜·麦克米伦-梅杰,施玛尔格·施密切,关于随机鹦鹉的危险:语言模型会不会过大? FAccT 2021。
-
蒂姆尼特·戈布鲁,有效利他主义推动一种危险的“AI 安全”品牌,Wired,2022 年。
-
克里希纳·加德,
www.linkedin.com/feed/update/urn:li:activity:7005573991251804160/ -
奇拉格·沙,艾米莉·本德,情境化搜索,CHIIR 2022。
-
为什么发布 GPT 和 ChatGPT 生成的回答目前不可接受,Stack Overflow,2022 年。
-
凯尔·维格斯,OpenAI 尝试给 AI 文本加水印遇到的限制,TechCrunch,2022 年。
-
7 个最佳大学论文写作服务:评论和排名,GlobeNewswire,2021 年。
-
卡尔汉·罗森布拉特,ChatGPT 被禁止在纽约市公立学校的设备和网络上使用,NBC 新闻,2023 年。
-
尼古拉斯·卡尔尼,弗洛里安·特拉默,埃里克·沃勒斯,马修·贾吉尔斯基,阿里尔·赫伯特-沃斯,凯瑟琳·李,亚当·罗伯茨,汤姆·布朗,道恩·宋,乌尔法尔·厄尔林森,阿丽娜·奥普雷亚,科林·拉费尔,从大型语言模型中提取训练数据,USENIX 安全研讨会,2021 年。
-
马丁·安德森,从预训练自然语言模型中检索现实世界的电子邮件地址,Unite.AI,2022 年。
-
玛丽·里根,理解 AI 系统中的偏见和公平性,Fiddler AI 博客,2021 年。
-
李·露西,戴维·班曼,GPT-3 生成故事中的性别和表现偏见,ACL 叙事理解研讨会,2021 年。
-
安德鲁·迈尔斯,剔除流行语言模型 GPT-3 中的反穆斯林偏见,斯坦福 HAI 新闻,2021 年。
-
詹姆斯·文森特,推特让微软的 AI 聊天机器人在不到一天的时间里变成了一个种族主义者,The Verge,2016 年。
-
比利·佩里戈,OpenAI 在肯尼亚以每小时不到 2 美元的工资雇佣工人来减少 ChatGPT 的毒性,《时代》杂志,2023 年。
-
Karthik Abinav Sankararaman, Sinong Wang, Han Fang, BayesFormer:具有不确定性估计的 Transformer,arxiv,2022 年。
-
Andrew Ng, ChatGPT 疯狂!加密混乱削减了 AI 安全资金,Alexa 讲睡前故事,《The Batch — Deeplearning.ai 通讯》,2022 年。
-
Emma Strubell, Ananya Ganesh, Andrew McCallum, 深度学习在 NLP 中的能源和政策考虑,ACL 2019 年。
-
Eric Wallace, Tony Z. Zhao, Shi Feng, Sameer Singh, 对 NLP 模型的隐蔽数据污染攻击,NAACL 2021 年。
-
Karen Hao, 训练单一 AI 模型可能排放相当于五辆汽车使用寿命的碳,《麻省理工学院技术评论》,2019 年。
不那么庞大的语言模型:优质数据打败巨人

(图像由 DALL·E 生成)
如何制造一个百万级别的语言模型来超越十亿级别的模型
·
关注 发表在 Towards Data Science · 6 min read · 2023 年 8 月 23 日
–
在这篇文章中,我们将探讨语言模型(LM)如何通过关注更好的数据和训练策略,而不仅仅依赖庞大的规模,来实现类似 LLM 的结果(有时甚至更好),以及人们如何已经成功且民主地做到这一点。
大型语言模型(LLMs)已经显著发展。它们带来了从生成类似人类的文本到理解复杂上下文的显著特性。虽然最初的兴奋主要集中在具有大量参数的模型上,但最近的发展表明,大小并不是唯一重要的因素。最近,一个新的概念“小型语言模型”(SLM)应运而生,致力于更智能地开发语言模型。
大模型的兴起
随着 LLMs 的出现,叙事变得简单明了——更大更好。具有更多参数的模型被期望能够更好地理解上下文,减少错误,提供更好的答案。但随着模型的增长,它们对计算资源的需求也增加了。训练这些巨型模型变得非常昂贵,这不是每个人都愿意(也不一定能)支付的。
对质量和效率的强调
认识到仅仅增加参数的不可持续性和递减回报,研究人员开始重新思考策略。与其只是将钱投入云端(增加更多的参数),一些研究人员转而利用更好的数据和更高效的训练策略。这个想法很优雅:一个训练良好的小模型可能会超越一个训练不良的大模型。但这可能吗?
Chinchilla 和 LLMs 训练的最佳点
“Chinchilla 论文” [1] 是对该领域的重要贡献,提供了对 LLMs 训练的有趣见解。实验似乎表明,在训练 LLMs 时存在一个“最佳点”。超过这个点,投入更多的资源(如更多参数)不一定会导致性能的成比例提高。论文强调,定义模型性能的不仅仅是模型的大小,而是数据的质量和使用的数据量。作者发现,为了实现计算最优训练,模型大小和训练令牌的数量应当等比缩放:每增加一倍的模型大小,训练令牌的数量也应增加一倍。
他们通过训练 Chinchilla(一个 70 亿参数的模型,训练于 1.4 万亿令牌)来测试这一点。尽管 Chinchilla 小得多,但在几乎所有评估中,包括语言建模、问答、常识任务等,Chinchilla 的表现都优于 Gopher。
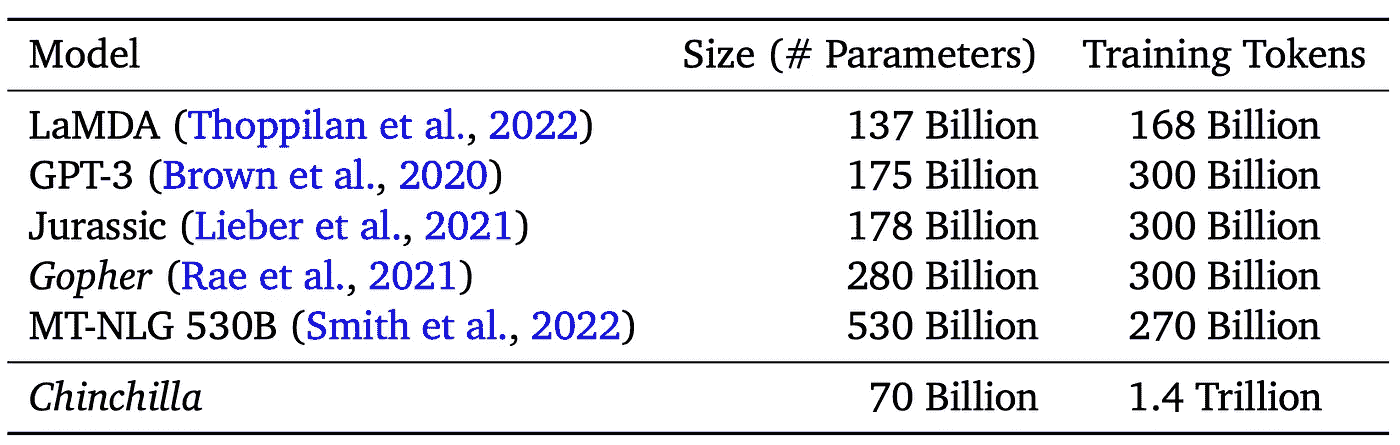
Chinchilla 的大小和训练令牌与 SOTA LLMs 的比较。(来源:[1])
即使在其减少的规模下,Chinchilla 在各种任务上的表现也优于其 SOTA 对手:

大规模多任务语言理解(MMLU)。报告了 57 项任务中的平均 5-shot 准确率,并与来自[2]的模型和人类准确率比较,以及来自[3]的 73 名竞争性人类预测者在 2022/2023 年 6 月的 SOTA 准确率的平均预测。(来源:[1])
阅读理解和自动推理是语言模型通常会测试的标准任务。它测试模型理解文本更广泛背景的能力。在我们的案例中,可以通过预测那些仅在模型能够理解单词与之前上下文关系的情况下才会预期到的单词来进行示例。通常使用基准测试和数据集,如 RACE-h、RACE-m [4] 和 LAMBADA [5] 进行评估。即使在这种难以定义和测试的任务中,Chinchilla 也超越了更大的模型。
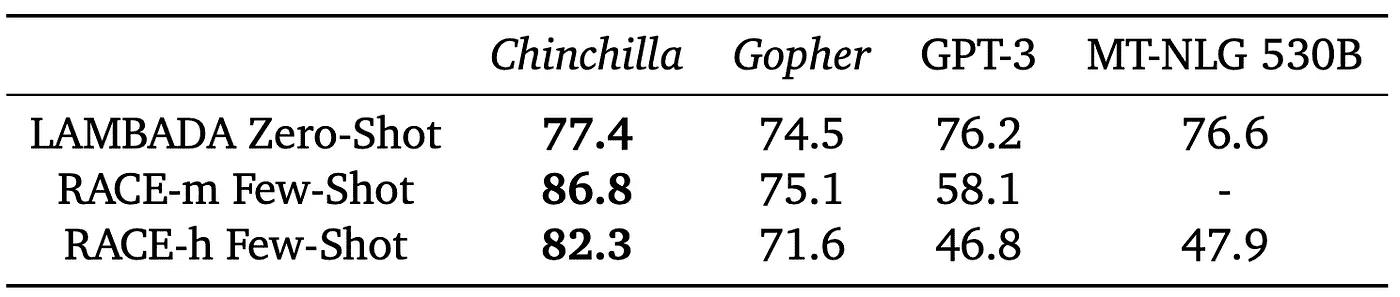
在阅读理解方面,Chinchilla 相比于 Gopher 显著提升了性能。(来源:[1])
Chinchilla 是许多尽管没有注重扩展规模但仍展现出有希望结果的语言模型之一。
LLaMA
LLaMA[6] 甚至更进一步。作者引入了从 7B 到 65B 参数的较小基础语言模型。它们在超过 1 万亿个标记的数据上进行训练,使用的仅是公开数据,使其兼容开源。
LLaMA-13B 在大多数基准测试中超过了参数多达 175B 的 GPT-3,而其体积小于 GPT-3 的 10 倍。作者认为,考虑到目标性能水平,训练时间更长的小型模型在给定计算预算下比大型模型更具优势,因为推理效率更高。
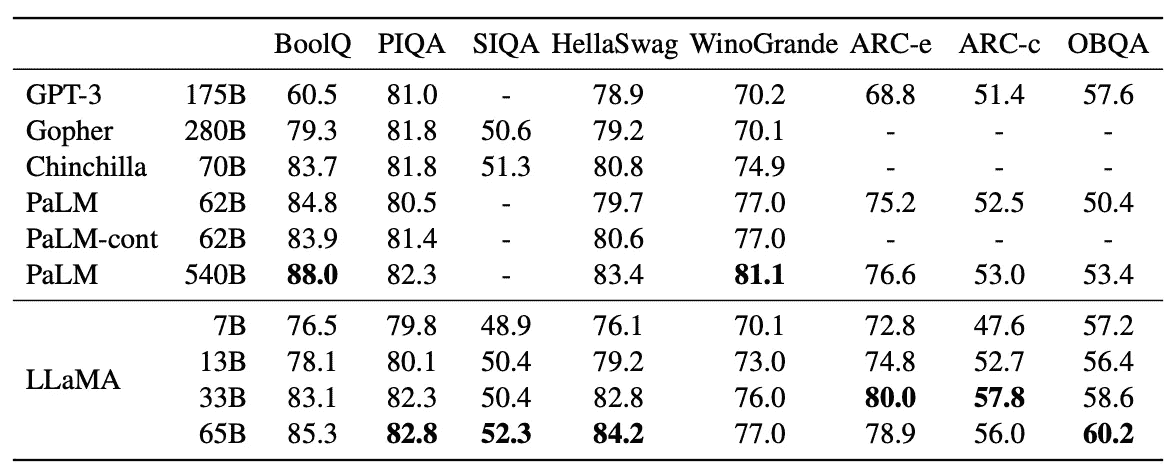
LLaMA 在常识推理任务中的零-shot 表现。(来源:[6])
一些项目甚至成功在预算有限的安卓智能手机上运行 LLaMA(或其版本),进一步证明我们正走在通过低计算资源实现语言模型民主化的正确道路上(LLaMA.c [7])。
LLaMA-65B(我知道,现在不算那么小,但仍然……)在与使用专有数据集的现有最先进模型如 PaLM-540B 的竞争中表现良好。这清楚地表明,优质数据不仅能提升模型的性能,还能使其变得民主化。机器学习工程师无需巨额预算就能在优质数据集上获得良好的模型训练。
优质数据胜过巨无霸
进一步巩固了语言模型不需要庞大才能表现良好的论点,TinyStories [8] 提供了一个合成数据集,其中包含仅供小孩子(最多四岁)理解的单词。它可以用来训练参数少于 1000 万的小型语言模型(SLMs),这些模型能够生成语法、推理和连贯性良好的多段故事。这与先前的研究形成对比,125M+ 参数的模型——如 GPT-Neo(小型)和 GPT-2(小型)——在生成连贯文本方面存在困难。

训练了 TinyStories 的模型能产生与参数大两个数量级的模型相当的输出。(来源:[8])
TinyStories 的一个令人兴奋的方面是数据集本身是由 GPT-3.5 和 GPT-4 创建的。作者们还引入了一种新的 SLM 评估范式,使用 GPT-4 对生成的故事在语法、情节和创意等维度上进行“评分”。这克服了标准基准测试要求受限输出的局限性。
结论
语言模型的发展展示了 AI 中的一个关键教训:更大并不总是更好。随着社区的持续进化和创新,人们意识到效率、数据质量和优化的训练策略是机器学习未来的关键。
关键要点
-
Chinchilla 证明了在训练语言模型时,令牌数量和训练数据质量之间存在一个最佳点。这一点与(或更重要于)模型参数的数量定义同样重要;
-
LLaMa 显示了使用仅公开数据就能达到类似 Chinchilla 的结果,证明了这一策略具有普遍可用性;
-
像 TinyStories 这样的数据集可以用于训练小型语言模型(少于 1 亿),在特定任务上超越了十亿规模的模型。
参考文献
[1] Hoffmann, Jordan 等. “训练计算最优的大型语言模型。” arXiv 预印本 arXiv:2203.15556(2022 年)。
[2] D. Hendrycks 等. “测量大规模多任务语言理解。” arXiv 预印本 arXiv:2009.03300(2020 年)。
[3] J. Steinhardt. 来自 AI 预测的更新和经验教训,2021 年。URL https://bounded-regret.ghost.io/ai-forecasting/。
[4] Lai, Guokun 等. “RACE: 大规模阅读理解数据集来自考试。” 2017 年自然语言处理会议论文集,页码 785–794,哥本哈根,丹麦。计算语言学协会。
[5] Paperno 等,2016 “LAMBADA 数据集:需要广泛语篇背景的单词预测。” arXiv:1606.06031(2016 年)。
[6] Touvron, Hugo 等. “LLaMA: 开放且高效的基础语言模型。” ArXiv abs/2302.13971(2023 年)
[7] github.com/karpathy/llama2.c
[8] Eldan, Ronen 和 Yuan-Fang Li. “TinyStories:语言模型可以小到什么程度仍然能够说出连贯的英语?” ArXiv abs/2305.07759(2023 年)
那么,为什么我们应该关心推荐系统呢?特邀:对汤普森采样的简要介绍
正在进行的推荐系统系列
·发布于 Towards Data Science ·阅读时间 12 分钟·2023 年 11 月 7 日
–

图片由 Myke Simon 提供,来源于 Unsplash
今天我发现自己再次陷入了相同的情境,连续第 100…01 天,一边浏览 Netflix 寻找观看的节目,一边拿着晚餐盒子吃饭。我的推荐内容中充斥着过多的亚洲浪漫和美国成长题材的建议,可能是基于我一个月或两个月前观看过的这些类别的某几部剧。 “这里没什么好看的…”–我一边阅读完所有简介一边叹了口气,自信地觉得自己能预测剧情的发展。我掏出了另一个备用的娱乐选项 Tiktok,同时潜意识里想着我可能需要不感兴趣一些视频,而喜欢、保存其他视频,以便…推荐算法今天给我推送一些新的内容流。
推荐系统(RecSys)可以被认为是一个已经非常成熟的算法,它已经深深植入我们的日常生活中,以至于在 1 到 Chat-GPT 的尺度上,它在学术界和非学术界都感觉像是 80 年代的趋势。然而,它绝不是一个近乎完美的算法。操作推荐应用程序所面临的伦理、社会、技术和法律挑战从未成为研究的前沿(就像大多数其他技术产品一样……)。例如,选择性群体的不公平和隐私侵犯是围绕 RecSys 的热门担忧,但这些问题仍未得到实施公司充分解决。此外,还存在许多更微妙的问题,通常没有得到足够的深思,其中之一是个体决策过程中的自主权丧失。一种“强大的”RecSys 无疑可以将用户推向某个方向[2],使他们购买、观看、思考、相信他们如果不受到这种操控本不会做的事情。
因此,我想在我的研究生学习旅程中写一系列文章,随着我开始学习并深入探讨 RecSys 的优缺点……一切从零开始!我觉得可以从思考电影和……汤普森采样开始!
汤普森采样
汤普森采样 (TS) 是推荐系统文献和强化学习中的基础算法之一。正如 Samuele Mazzanti 在这篇精彩的文章中清楚解释的那样,它可以被认为是在在线学习环境中更好的 A/B 测试。简单来说,在电影推荐的背景下,TS 试图识别出最适合推荐给我的电影,以最大化我点击观看的机会。它可以通过相对较少的数据有效地做到这一点,因为它允许在每次观察到我是否点击电影时更新参数。粗略地说,这种动态特性使得 TS 能够在考虑我的观看历史和收藏的系列之外,还能实时考虑像浏览或在我当前正在使用的应用程序中的搜索结果等因素,以给我最合适的建议。然而,在这个适合初学者的教程中,我们仅仅看一下下面的简化分析。
让我们进一步分析吧!
考虑这 3 部电影,尽管它们都很棒,但我却有自己个人的排名。假设这 3 部电影中,有一部是如果出现在我的推荐中我将 100%重新观看,有一部是我极不可能重新观看的(5%),还有一部是我每次看到时有 70%的机会会点击观看。显然,TS 在事先并不了解这些关于我的信息,它的目标是学习我的行为,以便,如常识所说,推荐我它知道我一定会点击观看的电影。

作者提供的图片
在 TS 算法中,主要的工作流程如下:
-
行动:TS 建议我观看特定的电影,在数百部电影中选择
-
结果:我决定电影对我来说足够有趣并点击观看,或者我觉得无聊,在阅读了简介后点击退出页面。
-
奖励:可以被看作是 TS 在我点击观看某部电影时获得的“积分”数量,或者在我不点击时 TS 失去的积分。在基本的电影或广告推荐设置中,我们可以将奖励视为结果的等价物,因此 1 次点击电影=1 积分!
-
更新知识:TS 记录我的选择并更新其对我最喜欢电影的信念。
-
重复第 1 步(可以在我当前的浏览会话中,或者第二天晚餐时间),但现在有了关于我偏好的额外知识。
探索/利用
这是该文献中使用最多的术语,也是区分 TS 和其他相关算法的关键。上述第 5 步是这个逻辑开始发挥作用的地方。在 TS 的世界中,一切都存在某种程度的不确定性。我每周喝三次拿铁和五次抹茶并不一定意味着我比拿铁更喜欢抹茶,如果只是那一周(而我每周平均实际上喝的拿铁比抹茶多)呢?因此,TS 中的一切都由某种类型的分布表示,而不仅仅是单个数字。

图 1 在某一周,我喝了 5 杯抹茶和 3 杯拿铁(左),但平均每周我喝的拿铁比抹茶多(右)——作者提供的图片
起初,TS 显然对我对电影的偏好有很多不确定性,因此它的优先任务是探索这一点,通过给我提供许多不同的电影建议来观察我的反应。在经过几次点击和跳过后,TS 可以大致了解我倾向于点击的电影和没有效益的电影,从而对下一次给我推荐的电影有了更多的信心。这时,TS 开始利用高回报的选项,它会给我推荐我经常点击的电影,但仍然留有一些探索的空间。随着更多观察的积累,信心不断建立,简单情况下,探索的工作将变得非常少,因为 TS 已经对能够带来大量奖励的推荐有了很大的信心。
探索与利用通常被称为权衡或困境,因为过多的探索(即使在获得足够证据后仍然没有排除低价值选项)会导致大量损失,而过多的利用(即过快地排除太多选项)可能会错误地排除真正的最佳行动。
分布:Beta-Bernoulli
如上面的抹茶拿铁图所示,TS 使用不同类型的分布来理解我们对不同选项的偏好。在最基本的电影(和广告)情况下,我们通常使用 Beta-Bernoulli 组合。
伯努利分布.) 是一种离散分布,其中只有两种可能的结果:1 和 0。伯努利分布只有一个参数,表示某个变量,比如 Y,取值为 1 的概率。因此,如果我们说 Y~ Bern§,比如 p = 0.7,这意味着 Y 有 0.7 的机会取值为 1,而 1–p = 1–0.7 = 0.3 的机会取值为 0。因此,伯努利分布适合用于建模奖励(在我们的例子中也是结果),因为我们的奖励只有两种结果:点击 或 未点击。
另一方面,Beta 分布用于建模 TS 对我电影兴趣的信念。Beta 分布有两个参数,alpha 和 beta,通常被认为是成功和失败的次数,两者都必须 ≥ 1。因此,使用 Beta 分布来建模我点击观看和跳过电影的次数是合适的。我们来看一个例子。这里有 3 个不同的 Beta 分布,代表 3 部电影,在 10 次观察中,所以所有 3 部电影的点击和跳过次数总和相同(10),但点击和跳过率不同。对于电影 1,我点击观看 2 次(alpha = 2)和跳过 8 次(beta = 8);对于电影 2,我点击观看 5 次和跳过 5 次;对于电影 3,我点击观看 8 次和跳过 2 次。

图 2. 图片由作者提供
根据图表,我们可以看到,我再次观看电影 2 的概率大约在 50% 处达到峰值,而电影 1 的这个概率要低得多。例如。我们可以将这些曲线视为观看电影的概率的概率,因此 Beta 分布非常适合表示 TS 对我电影偏好的信念。
算法
在本节中,我将帮助你清楚地理解算法的实现和方法论。首先,这是 Thompson Sampling 算法的一个片段,分别是伪代码和 Python 实现。伪代码摘自一本关于 TS 的精彩书籍,A tutorial on Thompson Sampling [Russo, 2017]。

图 3 Thompson Sampling,Python 实现(左)和伪代码(右)— 图片由作者提供
让我们来详细分析一下!
样本模型
算法的第一步涉及“猜测”我对每部电影的喜好。如前一节所述,我对每部电影的偏好可以使用 Beta 曲线表示,如图 2 所示,而 TS 对此没有先验知识,并且试图弄清楚这些 Beta 曲线的样子。在t = 1(第一轮)时,TS 可以假设我对所有 3 部电影的喜好相同,即点击和跳过的初始次数相等(我的 3 条 Beta 曲线将看起来相同)。
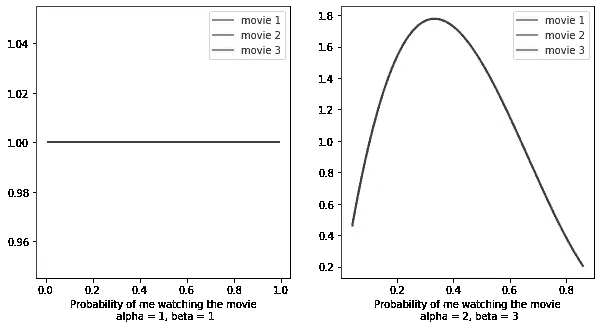
图 4 TS 对我对 3 部电影的偏好的首次猜测相同
这里的三种分布就是图 3 中伪代码中的p。从每个分布中,TS 将采样一个值,用 theta 表示,以帮助下一步的动作选择。

图 5 示例的 alpha-beta 值对,表示我们对每部 3 部电影的初始猜测的分布(也称为动作/手臂)
选择并应用动作
在此步骤中,TS 根据采样的 theta 值中最大的值选择要执行的动作(即选择推荐的电影)。以图 2 为例。假设我们只有 2 部电影——电影 1 和电影 3。使用最大的 theta 选择动作的想法是,如果真实分布几乎没有重叠,而我在我们的例子中几乎肯定喜欢一部电影多于另一部,那么电影 1 的采样 theta 很可能不会大于电影 3 的 theta。以类似的方式,如果我们只考虑电影 2 和 3,我们可以看到现在这些分布之间有更多重叠。然而,如果我们继续在足够多的轮次中采样更多的 theta 值,那么我们可以观察到电影 3 的 thetas > 电影 2 的 thetas 的比例大于反之,TS 将有足够的信息得出电影 3 是更好的“动作”的结论。一般来说,这也是为什么未知真实分布越明显,TS 找出哪个动作或手臂是最优的实验轮次就越少的原因。
在应用选择的动作后,TS 将收到我的反馈,即我是否点击观看电影。正如上面提到的,这一结果也被视为我们对相应动作的奖励。TS 将记录这一观察结果,并在下一步中用它来更新对我电影偏好的信念。
更新分布
在上面的 Beta 分布描述中,我们确定 Beta 分布的特征是成功次数和失败次数。我点击观看某部电影的次数越多,该电影的 Beta 分布的模式就越趋近于 1,而相反地,我跳过推荐的次数越多,模式就越趋近于 0。因此,在电影被推荐并记录响应后,对电影的信念更新是通过将电影的 Beta 分布的 alpha 或 beta 参数加 1 来完成的,具体取决于电影是被点击还是被跳过。
这种简单且易于解释的参数更新方法就是为什么 Beta Bernoulli 是一种非常常见的 TS 模型。
结果与讨论
回到文章开始时的情境。我们正在猜测 3 部电影中哪一部最适合推荐给我,假设有一部我会 100% 点击观看,一部我有 70% 的点击概率,另一部只有 5% 的点击概率(再次强调,这些信息 TS 并不知道)。第一行展示了两种不同的模拟起始点,这将使我们观察是否可以通过不同的初始先验信念达到相同的最终结果。
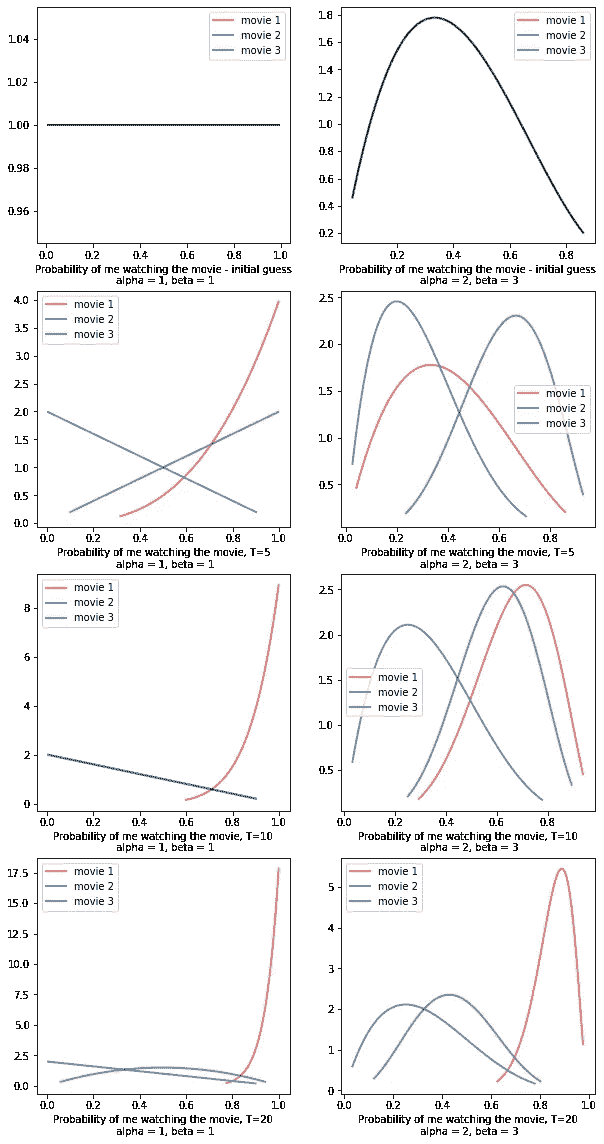
图 6 TS 模拟的不同轮数 T = 5, 10, 20。 Beta 分布代表了实验结束时 TS 对我电影偏好的信念。 左列:初始分布为 Beta(1, 1) 时的结果。右列:初始分布为 Beta(2, 3) 时的结果
从图 6 中,我们可以看到我最终最喜欢的电影是电影 1 — 《寄生虫》(对不起,漫威粉丝)!!
如我们所见,两种情况的探索过程不同,其中 Beta(1, 1) 的初始猜测导致更快地找到被认为是我最喜欢的电影。只需要 T=10 轮就可以看出 TS 明显在开发电影 1,这意味着 TS 已经推荐了电影 1 并得到了我的点击,因此其 Beta 分布向右拉动,因此从更新的分布中采样的 theta 超过了它的竞争对手,导致了开发。这种开发在 T=5 轮时已经出现,但根据相应的图表,电影 1 和电影 3 的 Beta 之间仍然存在较多重叠,它们的模式并不完全不同,这意味着 TS 仍然不完全确定电影 1 是最优的行动。
另一方面,Beta(2, 3) 的初始信念使得 TS 需要更多的轮次才能到达电影 1(T=20)。即使在 T=10 时,电影 1 和 电影 3 之间仍存在很大的不确定性,并且观察到由于 theta 采样的随机性,电影 3 可能被错误地当作最佳选项。这项实验表明,每个行动的初始先验知识在检测最佳臂的速度上起着作用,关于这个主题我们可以在未来的文章中进一步深入探讨。
需要注意的是,如果电影的实际分布几乎相同(比如电影 1 和电影 3 的点击率分别为 100% 和 98%),TS 很可能无法识别最佳行动,因为来自一个分布的样本 thetas 超过另一个分布的样本 thetas 的比例会被拆分。因此,如果由于偶然性,电影 3 的“较大 thetas”更多,TS 将更多地利用这个选项,导致其被错误地识别为最佳行动。
实验的另一个发现是,TS 仅能告诉我们最佳行动是什么,但不能提供关于其他选项的信息。这是因为在探索过程中,TS 会迅速淘汰那些被认为不是最优的选项,因此 TS 停止接收这些行动的进一步信息,从而不能提供最佳选项以外的行动的正确排序。
结论
在这篇文章中,我们探讨了汤普森采样算法,并通过电影推荐模拟进行了演练。汤普森采样在提供预测时涉及大量的分布和先验知识,这是贝叶斯模型的核心概念,我计划在即将到来的文章中与大家进一步讨论。如果你读到了这里,谢谢你的时间,希望这篇教程能给你提供对这个算法的技术和直观理解!如果你有任何进一步的问题,随时通过我的 LinkedIn 联系我,很高兴与您联系并回答问题!
参考文献:
[2] 推荐系统及其伦理挑战
[3] 何时应该选择“汤普森采样”而不是 A/B 测试
现在你看到我 (CME): 基于概念的模型提取
一种标签高效的基于概念的模型方法
·
关注 发表在 Towards Data Science ·6 分钟阅读·2023 年 9 月 22 日
–
来自 CIKM 会议上展示的 AIMLAI 研讨会论文:“Now You See Me (CME): 基于概念的模型提取” (GitHub)

视觉摘要。图片由作者提供。
总结
问题 — 深度神经网络模型是黑箱,无法直接解释。因此 — 很难建立对这些模型的信任。现有方法,如概念瓶颈模型,能够使这些模型更具可解释性,但需要高昂的标注成本来标注基础概念。
关键创新 — 一种以 弱监督方式 生成基于概念的模型的方法,从而显著减少注释需求
解决方案 — 我们的 基于概念的模型提取(CME)框架,能够以 半监督 方式从预训练的原始卷积神经网络(CNN)中提取基于概念的模型,同时保持最终任务性能。

原始 CNN 的端到端输入处理。作者提供的图像。
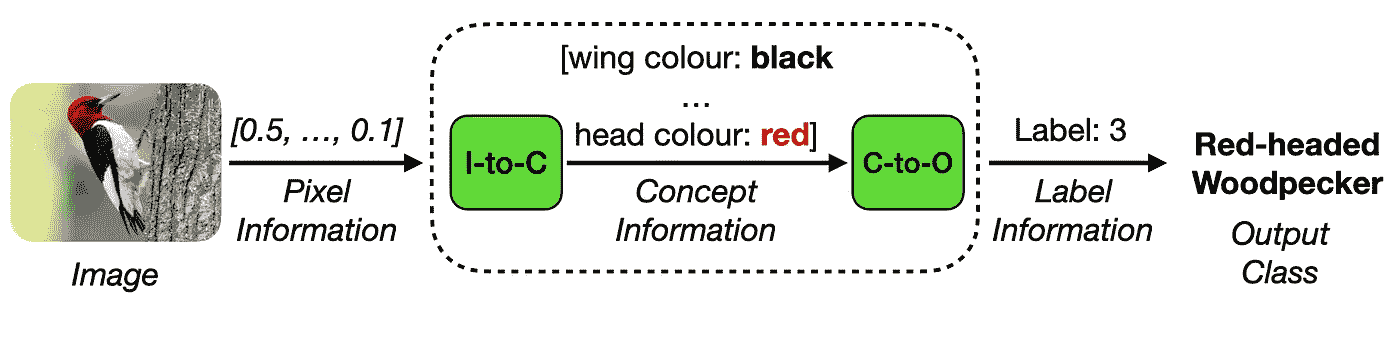
两阶段概念模型处理。作者提供的图像。
概念瓶颈模型(CBMs)
近年来,解释性人工智能(XAI)[1] 领域对概念瓶颈模型(CBM)方法 [2] 的兴趣激增。这些方法引入了一种创新的模型架构,其中输入图像分为两个不同的阶段处理:概念编码 和 概念处理。
在概念编码过程中,概念信息从高维输入数据中提取。随后,在概念处理阶段,提取的概念信息用于生成所需的输出任务标签。CBMs 的一个显著特点是它们依赖于具有语义意义的 概念表示,作为下游任务预测的中间、可解释的表示,如下所示:
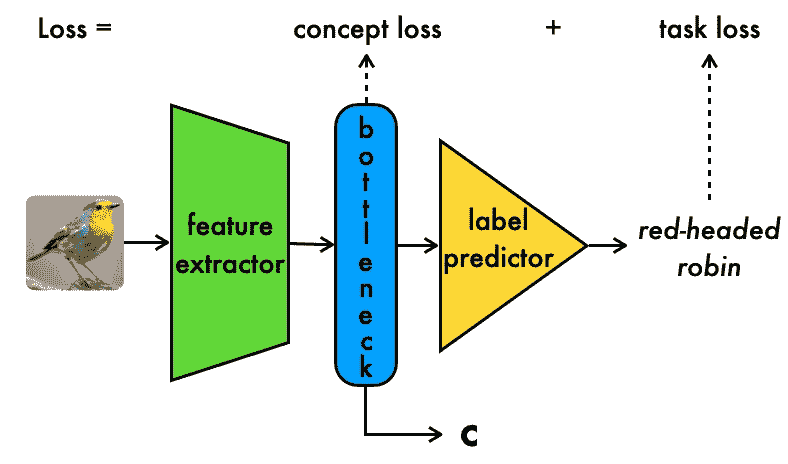
概念瓶颈模型处理。作者提供的图像。
如上所示,CBM 模型通过结合 任务损失 确保准确的任务标签预测,以及 概念损失 确保准确的中间概念预测进行训练。重要的是,CBMs 增强了模型的透明度,因为底层概念表示提供了一种解释和更好理解模型行为的方法。
概念瓶颈模型提供了一种新型的设计可解释的 CNN,允许用户通过概念将现有领域知识编码到模型中。
总体而言,CBMs 是一项重要的创新,使我们更接近于更透明和可信的模型。
挑战:CBMs 具有高概念注释成本
不幸的是,CBMs 在训练期间需要大量的概念注释。
目前,CBM 方法要求对 所有 训练样本进行显式注释,同时 包括最终任务和概念注释。因此,对于一个包含 N 个样本和 C 个概念的数据集,注释成本从 N 个注释(每个样本一个任务标签),增加到 N(C+1)* 个注释(每个样本一个任务标签,且每个概念一个概念标签)。在实践中,这可能迅速变得难以管理,特别是对于具有大量概念和训练样本的数据集。
例如,对于一个包含 10,000 张图片和 50 个概念的数据集,注释成本将增加 50*10,000=500,000 个标签,即增加 半百万 个额外注释。
不幸的是,概念瓶颈模型需要大量的概念标注进行训练。
利用 CME 的半监督概念模型
CME 依赖于 [3] 中强调的类似观察,其中观察到原始 CNN 模型通常在其 隐藏空间 中保留大量有关概念的信息,这可以用于无额外标注成本的概念信息挖掘。重要的是,这项工作考虑了基础概念 未知 的场景,并且必须以无监督的方式从模型的隐藏空间中提取。
使用 CME,我们利用上述观察,考虑一个场景,在该场景中,我们 已经 了解基础概念,但每个概念只有少量样本标注。类似于 [3],CME 依赖于给定的预训练原始 CNN 和少量概念标注,以 半监督的方式 提取进一步的概念标注,如下所示:

CME 模型处理。图片来源于作者。
如上所示,CME 使用预训练模型的隐藏空间以 事后 方式提取概念表示。详细信息见下文。
概念编码器训练:与 CBMs 处理原始数据的概念编码器从零开始训练不同,我们以 半监督的方式 设置概念编码器模型训练,使用原始 CNN 的隐藏空间:
-
我们首先预先指定一组层 L,从原始 CNN 中用于概念提取。这可以是 所有 层,也可以只是最后几层,具体取决于可用的计算能力。
-
接下来,对于每个概念,我们在 L 中 每个 层的隐藏空间上训练一个独立的模型,以预测该概念的值。
-
我们继续选择具有最佳模型准确度的模型和相应层作为“最佳”模型和层来预测该概念。
-
因此,在为概念 i 做出预测时,我们首先检索该概念的最佳层的隐藏空间表示,然后将其通过相应的预测模型进行推断。
总体来说,概念编码器 功能可以总结如下(假设总共有 k 个概念):
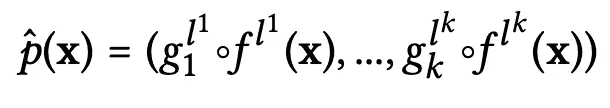
CME 概念编码器方程。图片来源于作者。
-
这里,LHS 上的 p-hat 代表概念编码器函数。
-
gᵢ 项代表在不同层隐藏空间上训练的隐藏空间到概念模型,i 代表概念索引,范围从 1 到 k。在实际应用中,这些模型可以非常简单,例如线性回归器或梯度提升分类器。
-
f(x) 项代表原始原始 CNN 的子模型,提取输入在特定层的隐藏表示。
-
在以上两种情况下,lʲ 上标指定了这两种模型操作的“最佳”层
概念处理器训练:CME 中的概念处理器模型训练是通过使用任务标签作为输出、概念编码器 预测作为输入来设置的。重要的是,这些模型操作在更紧凑的输入表示上,因此可以通过可解释的模型(如决策树(DTs)或逻辑回归(LR)模型)直接表示。
CME 实验与结果
我们在合成数据集(dSprites 和 shapes3d)以及具有挑战性的真实数据集(CUB)上的实验表明,CME 模型:
- 实现高概念预测准确度,在许多情况下可与 CBM 相媲美,即使在与最终任务无关的概念上:

CBM 和 CME 模型的概念准确度,绘制了三个不同预测任务中的所有概念。图像由作者提供。
- 允许对概念进行人为干预 — 即允许人们通过修正少量选定概念来快速改善模型性能:
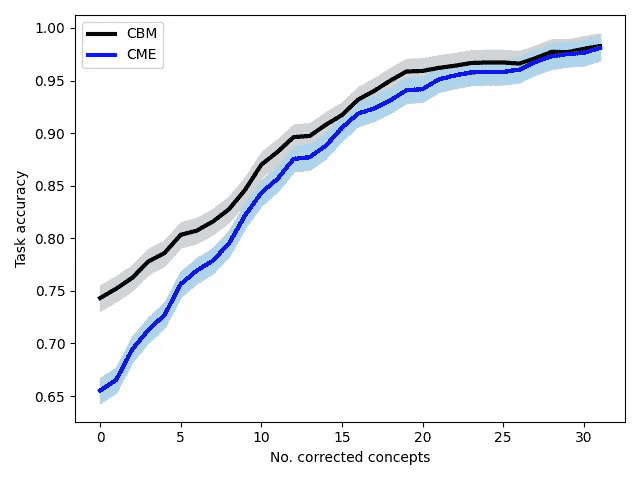
CME 和 CBM 模型性能在不同概念干预程度下的变化。图像由作者提供。
- 从概念的角度解释模型决策, 允许实践者直接绘制概念处理器模型:

一个概念处理器模型直接可视化的示例,针对一个选定任务。图像由作者提供。
- 通过分析模型层间的隐藏空间,帮助理解模型对概念的处理:
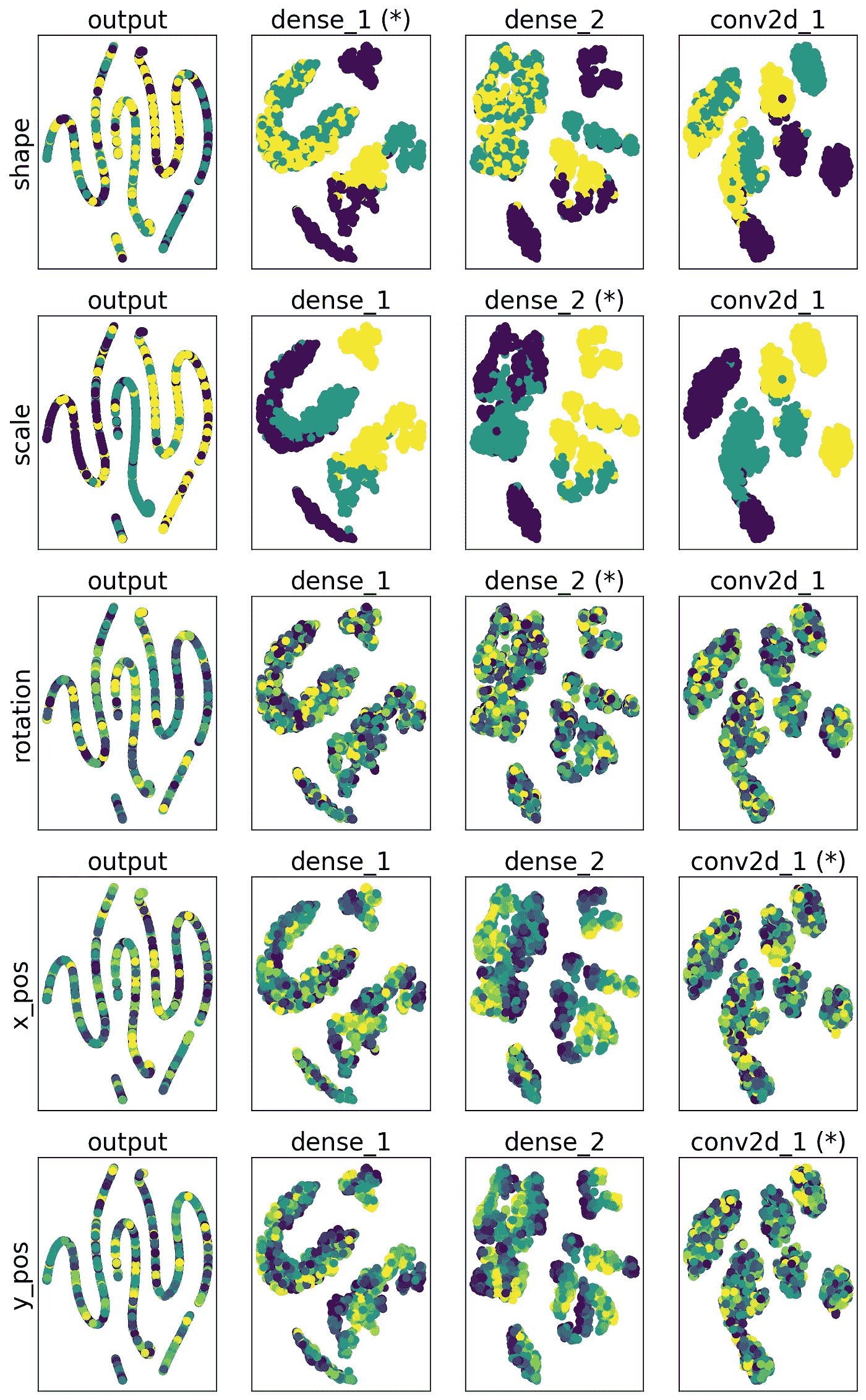
一个简单 CNN 的隐藏空间可视化示例。列代表不同的层,行代表不同的概念,每行的颜色对应于该概念的值。标有 * 的为“最佳” CME 层。图像由作者提供。
通过在弱监督领域定义基于概念的模型(CME),我们可以开发出显著更具标签效率的基于概念的模型
主要结论
通过利用预训练的普通深度神经网络,我们可以在极大降低注释成本的情况下获得概念注释和基于概念的模型,与标准 CBM 方法相比。
此外,这不仅严格适用于与最终任务高度相关的概念,在某些情况下,也适用于与最终任务独立的概念。
参考文献
[1] Chris Molnar. 解释性机器学习。 christophm.github.io/interpretable-ml-book/
[2] Pang Wei Koh, Thao Nguyen, Yew Siang Tang, Stephen Mussmann, Emma Pierson, Been Kim, 和 Percy Liang. 概念瓶颈模型。在国际机器学习会议,第 5338–5348 页。PMLR*(2020)。
[3] Amirata Ghorbani, James Wexler, James Zou, 和 Been Kim. 朝向自动化基于概念的解释。在 神经信息处理系统的进展,32。
np.stack() — 如何在 Numpy 和 Python 中堆叠两个数组
原文:
towardsdatascience.com/np-stack-how-to-stack-two-arrays-in-numpy-and-python-fc910dd2d57a
Numpy 中堆叠的初学者和高级示例——学习如何轻松地连接数组序列
·发表于Towards Data Science ·阅读时间 7 分钟·2023 年 1 月 10 日
–

图片由Brigitte Tohm提供,来源于Unsplash
Numpy 是一个在数据科学和机器学习中非常出色的库,因此如果你想成为数据专业人士,就必须掌握它。掌握这个包的方方面面是必要的,因为重新发明轮子是没有意义的——几乎你能想到的任何东西都已经实现了。
今天你将了解所有关于 np stack 的信息——即 Numpy 的stack()函数。简单来说,它允许你按行(默认)或按列连接数组,具体取决于你指定的参数值。我们将讨论基础知识和函数签名,然后进入 Python 中的示例。
什么是 np stack?
Numpy 的 np stack 函数用于在新轴上堆叠/连接数组。它将返回一个单一数组,作为堆叠多个形状相同的序列的结果。你也可以堆叠多维数组,稍后你将很快学到这一点。
但首先,让我们解释一下水平堆叠和垂直堆叠的区别。
Numpy 中的水平堆叠与垂直堆叠
水平堆叠数组意味着你将具有相同维度的数组堆叠在彼此之上。每个输入数组将在结果数组中成为一行。
查看下面的图像以更好地理解:
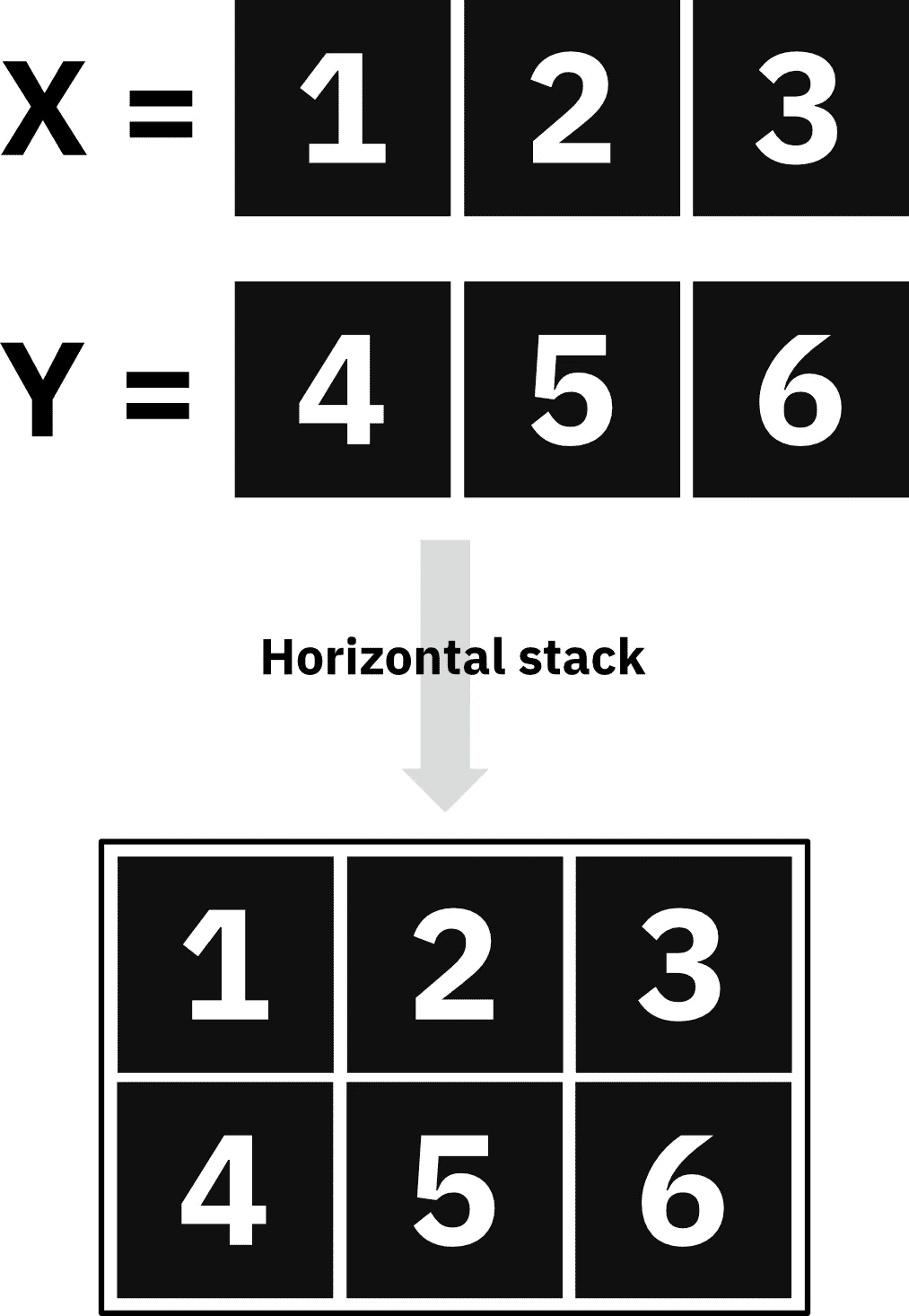
图 1 — 解释水平堆叠(图像由作者提供)
垂直堆叠则完全相反。两个垂直堆叠数组的一行包含来自两个数组的对应元素。
例如,垂直堆叠数组 Z 的第一行将包含输入数组 X 和 Y 的第一个元素。
也许你会发现视觉上更容易理解:

图 2 — 垂直堆叠解释(图片由作者提供)
说到这里,让我们看看 np.stack 函数的签名。
函数参数解释
np.stack 函数最多可以接受三个参数,其中只有第一个是必需的:
-
arrays- 数组的序列,或你想要堆叠的数组数组 -
axis- 整数,沿着你想要堆叠数组的轴(0 = 按行堆叠,1 = 对于一维数组按列堆叠,或使用 -1 使用最后一个轴) -
out- 可选的结果存放位置。如果提供,输出数组的形状必须与堆叠结果的形状匹配
理论讲解够了!现在我们来看看一些实际的示例。
Numpy 堆叠实战 — 函数示例
我们讨论了很多关于水平和垂直堆叠的内容,所以让我们看看它在实践中的表现。
Numpy 水平堆叠(按行)
要水平堆叠两个 numpy 数组,只需调用 np.stack 函数并传入这些数组。无需其他参数:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Horizontal (row-wise) stacking #1
arr_stacked = np.stack([arr1, arr2])
print('Numpy horizontal stacking method #1')
print('-----------------------------------')
print(arr_stacked)
这是得到的结果:

图 3 — Numpy 中的水平堆叠 (1)(图片由作者提供)
如你所见,输出看起来很像 Pandas DataFrame 的 Numpy 版本,这意味着一个数组几乎等于矩阵的一行。
更明确地说,你可以通过将 axis=0 作为第二个参数来实现相同的结果:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Horizontal (row-wise) stacking #2
arr_stacked = np.stack([arr1, arr2], axis=0)
print('Numpy horizontal stacking method #2')
print('-----------------------------------')
print(arr_stacked)
结果是相同的:

图 4 — Numpy 中的水平堆叠 (2)(图片由作者提供)
接下来,让我们探索垂直堆叠。
Numpy 垂直堆叠(按列)
要垂直堆叠两个 numpy 数组,只需将 axis 参数的值更改为 1:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Vertical (column-wise) stacking #1
arr_stacked = np.stack([arr1, arr2], axis=1)
print('Numpy vertical stacking method #1')
print('---------------------------------')
print(arr_stacked)
现在,数组按列堆叠,这意味着你将有与提供的数组数量相等的列:

图 5 — Numpy 中的垂直堆叠 (1)(图片由作者提供)
使用简单的一维数组,你还可以设置 axis=-1 来垂直堆叠数组:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Vertical (column-wise) stacking #2
arr_stacked = np.stack([arr1, arr2], axis=-1)
print('Numpy vertical stacking method #2')
print('---------------------------------')
print(arr_stacked)
结果是相同的:

图 6 — Numpy 中的垂直堆叠 (2)(图片由作者提供)
接下来,让我们讨论一些关于堆叠 N 维数组的内容。
使用 stack() 合并一维数组
你已经看到如何堆叠一维数组了,下面是回顾:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Stacking 1D arrays
arr_stacked = np.stack([arr1, arr2])
print('Numpy stacking 1D arrays')
print('------------------------')
print(arr_stacked)
输出结果:

图 7 — 堆叠一维数组(图片由作者提供)
记住,如果你想按列堆叠数组,可以更改 axis 参数的值。
使用 stack() 合并二维数组
对于使用 np.stack 堆叠二维数组,过程是一样的。这是一个示例:
import numpy as np
arr1 = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8]
])
arr2 = np.array([
[9, 10, 11, 12],
[13, 14, 15, 16]
])
# Stacking 2D arrays #1
arr_stacked = np.stack([arr1, arr2])
print('Numpy stacking 2D arrays method #1')
print('----------------------------------')
print(arr_stacked)
我们现在得到一个三维数组,每个元素是两个水平堆叠数组的二维数组:

图 8 — 堆叠二维数组 (1)(图片由作者提供)
一如既往,你可以垂直堆叠二维数组:
import numpy as np
arr1 = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8]
])
arr2 = np.array([
[9, 10, 11, 12],
[13, 14, 15, 16]
])
# Stacking 2D arrays #2
arr_stacked = np.stack([arr1, arr2], axis=1)
print('Numpy stacking 2D arrays method #2')
print('----------------------------------')
print(arr_stacked)
以下是输出结果:

图像 9 — 堆叠 2D 数组(2)(作者提供的图像)
这就是 numpy 堆叠的基本知识了。接下来,我们将介绍一些高级用法示例和常见问题。
高级:循环中的 np stack
常见的问题之一是如何在循环中使用 np stack。这里有一个示例 —— 它将两个二维数组首先合并为一个三维数组:
import numpy as np
arr1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
arr2 = np.array([[13, 14, 15], [16, 17, 18]])
matrix = [arr1, arr2]
print('Numpy stacking in a loop - intermediary matrix')
print('----------------------------------------------')
print(matrix)
这是中间输出:

图像 10 — 循环中的 Numpy 堆叠(1)(作者提供的图像)
现在,要生成一个水平堆叠元素的二维数组,你可以使用循环:
arr3 = np.empty(shape=[0, matrix[0].shape[1]])
for m in matrix:
arr3 = np.append(arr3, m, axis=0)
print('Numpy stacking in a loop')
print('------------------------')
print(arr3)
结果如下:

图像 11 — 循环中的 Numpy 堆叠(2)(作者提供的图像)
现在我们将讨论一些关于 Python 中 np stack 函数的常见问题。
常见问题
stack 和 concatenate 有什么区别?
简而言之,当传入两个一维数组时,np stack 函数将返回一个二维数组。而 np concatenate 函数则将所有输入数组的元素合并为一个一维数组。
什么是 numpy dstack?
numpy dstack 函数允许你按索引合并数组,并将结果存储为堆栈。这是一个示例:
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([5, 6, 7, 8])
# Numpy depth stacking - dstack
arr_stacked = np.dstack([arr1, arr2])
print('Numpy depth stacking')
print('--------------------')
print(arr_stacked)
print()
print(f'Shape = {arr_stacked.shape}')
输出结果:

图像 12 — Numpy dstack(作者提供的图像)
因此,我们有两个 1x4 的数组进来,dstack 将它们垂直地合并成一个三维数组格式。这对于某些用例来说非常方便。
喜欢这篇文章吗?成为 Medium 会员 以继续无限学习。如果你使用以下链接,我将获得你的会员费的一部分,但对你没有额外费用。
medium.com/@radecicdario/membership
最初发表于 https://betterdatascience.com ,日期为 2023 年 1 月 10 日。
NP-什么?优化问题的复杂性类型解释
原文:
towardsdatascience.com/np-what-complexity-types-of-optimization-problems-explained-558d43276044

复杂的建筑。图片由作者使用 Midjourney 创建。
计算机科学中的一个核心问题介绍
·发布于 Towards Data Science ·阅读时间 11 分钟·2023 年 8 月 17 日
–
为什么 最短路径问题 容易解决,而 旅行推销员问题 却不容易?这些问题的数学原理是什么?如何确定如果问题规模增加,是否会需要不可管理的步骤?在这篇文章中你将了解这个主题的基础知识。如果你想深入了解,我在文章末尾还附上了与这个主题相关的千年大奖难题的简要说明。
在我们开始讨论 NP 难度之前,你应该了解时间复杂度的基础。如果你熟悉时间复杂度、大 O 符号和最坏情况分析,你可以跳过以下部分。
时间复杂度
当我们使用计算机编程时,我们经常会遇到可以用不同方式解决的问题。我们需要考虑的一个重要方面是这些解决方案的效率。时间复杂度帮助我们理解当问题规模变大时,算法运行的速度如何。
大 O 符号 可以比作用一个简单的标签来标记算法,这个标签告诉我们算法完成所需的时间,基于我们处理的事物数量。这是一种描述算法步骤数量相对于问题输入规模增长的方式。
注意:时间复杂度本质上与步骤数量有关,而不是实际时间,因此这个名字不太准确。否则你可以使用更快的计算机和相同的算法。

给箱子(算法)贴上标签:你有多快?作者提供的图片。
我们通常关注最坏情况,因为我们希望确保无论我们给算法什么输入,它都不会花费超过一定的时间。这有助于确保我们的解决方案在情况变得困难时仍然可靠。

如果你正在寻找一本书中的特定页面,而你的算法从书的开头查到结尾,最坏的情况就是那一页是最后一页。作者提供的图片。
就像我们驾驶时选择最快路线一样,我们也希望为我们的问题选择最有效的算法。我们根据算法的时间复杂度来比较算法。一个运行更快(时间复杂度更低)的算法就像是选择更快的路线到达目的地。如前所述,一个更快的算法在最坏情况下需要的步骤更少。
现在,让我们通过一些实际的例子来探讨这些概念,使其更清晰。
常数时间:O(1)
想象一下你在计划去附近的公园旅行。你就住在公园旁边,所以无论你邀请多少朋友,步行到公园所需的时间始终不变。无论是你一个人还是一群 10 人,前往公园所需的时间都是恒定的——它不会因人数的不同而改变。

去公园的时间大致相同,不论人数多少。作者提供的图片。
常数时间的编程例子是使用一个键在字典中找到对应的值。
线性时间:O(n)
现在,想象一下计划一次野餐并召集所有朋友。当你邀请每个朋友时,你需要单独打电话或发消息。所以,如果你邀请 10 个朋友,你就打 10 个电话;如果你邀请 50 个朋友,你就打 50 个电话。联系朋友所需的时间随着朋友数量的增加而线性增长。
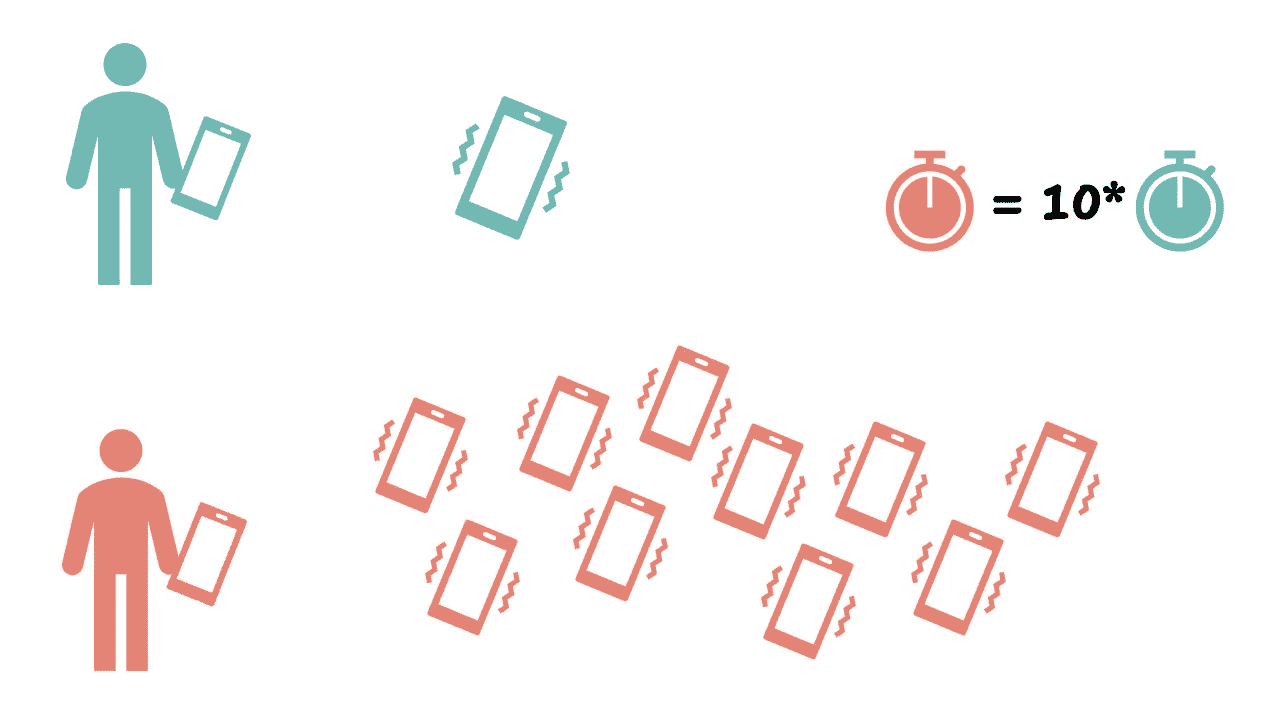
邀请一个朋友或 10 个朋友是有区别的:邀请 10 个朋友需要的时间大约是邀请 1 个朋友的 10 倍。作者提供的图片。
如果你遍历列表中的所有项目一次,这需要线性时间。
对数时间:O(log n)
在公园里,你将玩一个需要寻找隐藏宝藏的游戏。游戏会给你线索,帮助你缩小搜索区域。每个线索帮助你排除掉公园的一半。随着你找到更多的线索,搜索区域变得更小。另一种看法是:如果公园的面积是 100 平方米,那么找到宝藏最多需要 7 步(2⁷ = 128)。即使公园面积增加了 1 平方米,也没有关系,它仍然需要 7 步(101 < 128)。直到我们达到 128 之前,最坏情况下我们永远不需要额外的步骤(这里的最坏情况是什么?)。

每一步将搜索空间减少 50%。额外的一平方米不会有太大区别。图片由作者提供。
这类似于二分搜索的工作原理,其中每个线索都将可能的位置数量减少一半,导致对数时间复杂度。
二次时间:O(n²)
你正在尝试规划一个公路旅行,访问城市中的各种旅游景点。为了找出每对位置之间的最短路线,你需要将每个位置与其他每个位置进行比较。因此,如果你有 5 个位置,你需要进行 5 * 4 = 20 次比较;如果你有 10 个位置,你需要进行 10 * 9 = 90 次比较。随着位置数量的增加,比较次数会二次增长。
mylist = [1, 2, 3, 4, 5]
for n in mylist:
for m in mylist:
print(n*m)
嵌套的 for 循环是一个例子,它需要二次时间。你要对所有元素进行两次循环,因此需要 n * n 次迭代。上面的代码示例将打印 5 * 5 = 25 个数字。
阶乘时间:O(n!)
最后但同样重要的是:阶乘时间。想象一下,你正在和朋友们组织一次盛大的旅行冒险。你想规划一个访问所有愿望列表上的国家的最佳路线。然而,找到最佳路线涉及考虑所有可能的国家排列。随着你在列表中添加更多国家,可能路线的数量会按阶乘增长。例如,如果你有 3 个国家,有 3! = 6 种可能的路线(ABC,ACB,BAC,BCA,CAB,CBA)。如果你有 4 个国家,则有 4! = 24 条路线,依此类推。
在这种情况下,随着你在列表中增加国家的数量,考虑所有可能路线所需的时间会因阶乘增长而急剧增加。这反映了阶乘时间复杂度,其中所需的时间随着输入规模的增加而极快增长。正如规划行程随着你添加更多国家而变得繁重一样,阶乘时间复杂度由于其快速增长在处理大问题时变得不可行。
我们可以在图表中可视化时间复杂度。绿色的是快速的,而橙色和红色的是在 n 增加时难以处理的。如果可能的话,你应该尽量避免这些。
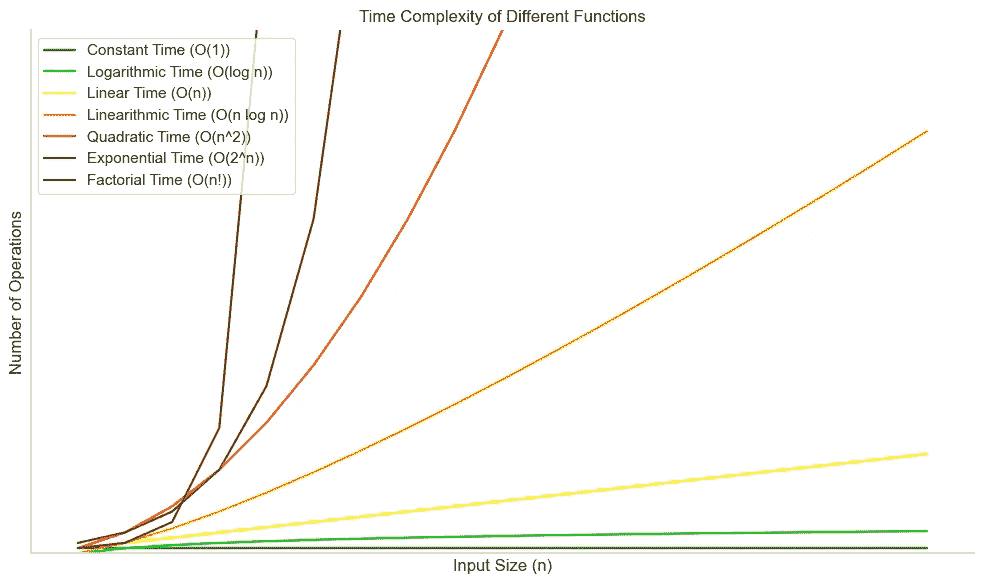
与输入大小相关的不同 Big O 时间复杂度的操作数量。图片由作者提供。
让我们深入了解这与 NP-难度的关系。
NP-难度
常数、线性和二次时间是多项式时间的例子。多项式时间的形式是 O(nˣ)。如果我们将多项式时间与指数和阶乘时间进行比较,你会发现对于大值 n 有很大的差异:

看看粉色数字,它们展示了随着数据大小的增加,指数和阶乘时间复杂度函数如何增加。点击放大。图片由作者提供。
如表所示,多项式时间与指数时间和阶乘时间之间存在巨大差异。对于大值 n,多项式时间是相对快速的,对于 n < 100 不超过 1 秒,而指数时间和阶乘时间则无法管理。(尽管如果 n 的值非常大,多项式时间仍可能需要相当长的时间。)
NP-难度的概念有助于根据计算复杂度对问题进行分类。问题分为四个类别,其中最简单的区分是 P 问题和 NP 问题之间的区别。
P 问题
P 问题,其中 P 代表多项式,是可以在多项式时间内解决的。换句话说,它们的解决方案可以相对快速地找到,解决它们所需的时间最多是问题规模的多项式函数。
一个数学优化问题的例子,它属于 P 问题,是最短路径问题。如何在最小化距离的情况下从点 A 到点 B?迪杰斯特拉算法 是一个可以在多项式时间内解决这个问题的算法(或者通过优先队列更少的时间)。
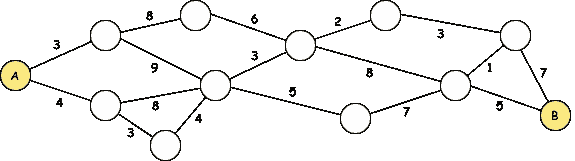
从 A 到 B 的最短路径是什么?图像由作者提供。
NP 问题
另一方面,NP 问题(或非确定性多项式问题)涵盖了更广泛的挑战。这些问题的特点是提出的解决方案可以在多项式时间内有效验证。然而,找到解决方案本身可能需要指数级或甚至阶乘时间,使得它们比 P 问题更难解决。换句话说:如果你处理的是一个大型 NP 问题,尝试暴力破解是愚蠢的。
NP 问题是汉密尔顿路径问题:给定一个图,是否存在一条路径访问每个顶点一次并返回到起始顶点?如果有人声称他们找到了一个汉密尔顿路径,你可以通过检查它是否确实访问了每个顶点一次来验证。

验证黄色路径是否为汉密尔顿路径很简单。图像由作者提供。
在 NP 问题的范围内,我们遇到两个子类别:NP 完全问题和 NP 难问题。
NP 完全问题
在 NP 问题中,NP 完全问题是最具挑战性的。NP 完全问题是指属于 NP 且具有一个特殊属性的问题:如果你能找到一个多项式时间算法来解决它,你就能在多项式时间内解决所有 NP 问题。实质上,NP 完全问题是 NP 中“最难”的,因为它们至少与 NP 中的其他任何问题一样困难。
最著名的 NP-完全问题之一是旅行商问题(TSP),你需要找到一条最短的路线,同时访问所有给定的位置一次。可能的路线数量可以用 n!计算,其中 n 是要访问的位置数量。在之前的文章中,我使用了混合整数规划(第二个示例)和模拟退火(第一个示例)对 TSP 进行了编码。与之密切相关的是中国邮差问题,你需要至少访问图中的每条边一次。
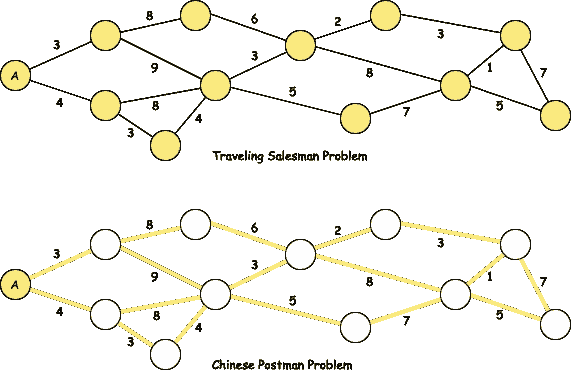
TSP:访问每个节点。中国邮差问题:至少访问每条边一次。这两个都是 NP-完全问题。图片由作者提供。
NP-困难问题
NP-困难问题虽然相关,但与 NP-完全问题不同。NP-困难问题是指至少与 NP 中最难的问题一样困难的问题,不管它是否在 NP 中。换句话说,NP-困难问题不一定具有像 NP 中那样的高效验证过程。相反,它们作为极其困难的计算问题的基准。
停机问题询问的是,给定一个程序和输入,该程序是否会在该输入上停止(停止执行)或无限运行。它是不可判定的,这意味着没有算法可以在所有情况下解决它。停机问题是 NP-困难的,但不在 NP 中,因为它的解决方案无法高效验证。在下一个代码片段中,你会看到停机问题的两个简单示例,对于其他程序,确定其是否为停机问题可能是有问题的。
# Example 1\. Program with the following code will keep running
while True:
continue
# Example 2\. Program with only a print statement will halt after printing
print('Halt')
总结来说,计算复杂度的范围包括从易于解决到极具挑战性的问题。虽然 P 问题可以高效解决,但 NP 问题引入了一层复杂性,其中 NP-完全问题代表了 NP 类中计算难度的巅峰。此外,NP-困难问题提供了对计算可行性边界的见解,即使它们不直接属于 NP 类。

如果我们假设 P ≠ NP(更多内容在最后一部分),这就是 P、NP、NP-完全和 NP-困难问题集合的欧拉图。图片由作者提供。
不幸的是,NP 问题在现实生活中无处不在。例如,优化配送卡车的路线、高效安排任务、设计电子电路,甚至蛋白质折叠都是 NP 问题的实例。这些问题的难处理性使得寻找最佳解决方案成为一项巨大的挑战:它们在大输入下 notoriously 难以解决。这种困难通常导致了近似算法、启发式方法和专门技术的发展,以寻找可能不是最优但在某些范围内可接受的解决方案。

如何书写历史?继续阅读以了解更多!照片由 Natalia Y. 提供,来源于 Unsplash
千年奖问题:P 对 NP
NP 硬度与其中一个未解的千年奖问题有关。这个问题很容易理解。如果你能证明 P = NP 或者 P ≠ NP,你就解决了它!这意味着什么?正如你现在所知道的,P 问题在大 n 下需要的步骤远少于 NP 完全问题。但从未证明 P 问题与 NP 问题确实不同,这意味着尚不确定是否存在多项式时间算法来解决 NP 问题。如何解决这个问题?有两种可能的结果:
-
如果你能找到一个解决 NP 完全问题(例如旅行商问题)的多项式时间算法,你就证明了 P = NP。
-
如果你能证明不存在多项式时间算法来解决特定的 NP 问题,你就证明了 P ≠ NP。你可能需要提出一个新的 NP 完全问题来实现这一点。
证明第一个观点将震撼世界,因为互联网安全是建立在 NP 硬度的基础上的。如果能够找到破解代码的多项式时间算法,那将是灾难性的。许多科学家认为第二种结果是正确的,即不存在能够解决 NP 完全问题的多项式时间算法。但这从未被证明。如果你想书写历史,这就是你的机会!
结论
深入探讨计算复杂性的细节揭示了计算机科学中问题解决的挑战。时间复杂性让我们能够在问题规模增长时评估算法效率。通过这种视角,我们探讨了常数、线性、对数、平方和阶乘复杂度等场景。
转向 NP-困难性,我们探索了各种复杂度的问题。P 与 NP 问题尤为突出——P 问题可以在多项式时间内解决,而 NP 问题则提供快速验证,但通常需要指数级或阶乘时间才能找到解决方案。NP 完全问题和 NP-困难问题成为计算挑战的巅峰。NP 完全问题涵盖了 NP 中的“最难”问题,提供了高效解决所有 NP 问题的捷径。NP-困难问题不局限于 NP,代表了计算复杂性的顶峰。
最后,P 与 NP 问题的谜团——一个难以捉摸的千年难题——有潜力重塑我们对计算复杂性的理解。这个问题的深远影响使得证明 P = NP 或 P ≠ NP 的探索者有可能改变历史的进程。
相关
数据科学课程目前关注数据可视化、特征工程、数据处理、(有/无)监督学习……
towardsdatascience.com ## 五种将数学优化与机器学习结合的方法
结合两种力量的实际例子。
towardsdatascience.com ## 精确算法还是启发式算法?
逐步指南,帮助你为数学优化问题做出正确选择
towardsdatascience.com
NT-Xent(归一化温度调节交叉熵)损失函数的解释及在 PyTorch 中的实现
一种直观解释 NT-Xent 损失函数的方法,详细解释其操作,并在 PyTorch 中进行了实现
·
关注 发表在Towards Data Science ·14 min read·Jun 13, 2023
–
与Naresh Singh合作撰写。
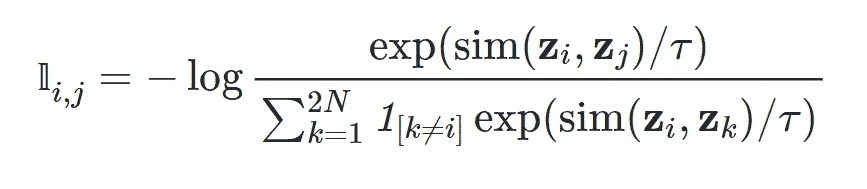
NT-Xent 损失函数公式。来源:Papers with code (CC-BY-SA)
介绍
最近在 自监督学习 和 对比学习 方面的进展激发了机器学习(ML)领域的研究人员和从业者重新关注这一领域。
尤其是,SimCLR 论文提出了一个简单的对比学习视觉表示框架,在自监督和对比学习领域获得了大量关注。
论文的核心思想非常简单——允许模型学习一对图像是否来自相同或不同的初始图像。
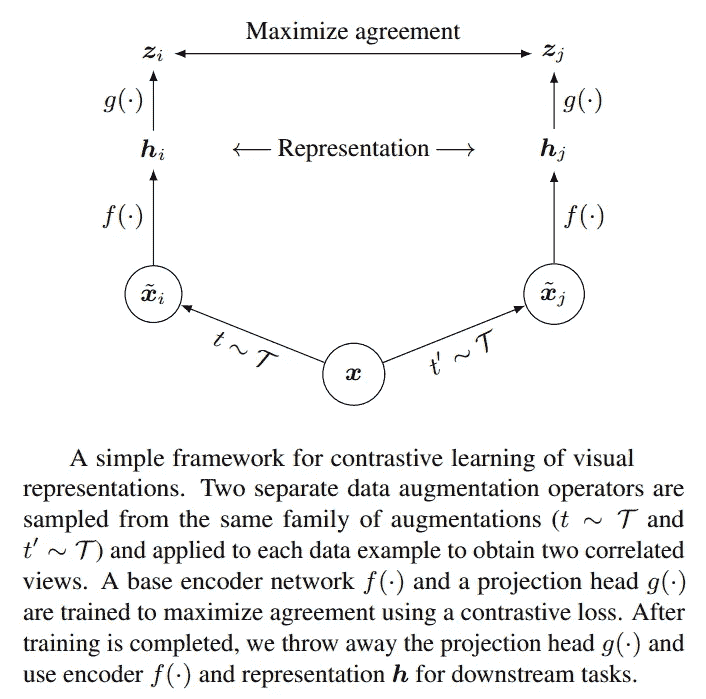
图 1:SimCLR 的高层次思路。来源:SimCLR 论文
SimCLR 方法将每个输入图像 i 编码为特征向量 zi。需要考虑两种情况:
-
正对:相同图像使用不同的增强集合进行增强,结果特征向量 zi 和 zj 进行比较。这些特征向量通过损失函数被强制保持相似。
-
负对:不同的图像使用不同的增强集合进行增强,结果特征向量 zi 和 zk 进行比较。这些特征向量通过损失函数被强制保持不相似。
本文其余部分将集中于解释和理解该损失函数及其使用 PyTorch 的高效实现。
NT-Xent 损失
从高层次看,对比学习模型接收 2N 张图像,来源于 N 个基础图像。每个 N 个基础图像都使用随机的图像增强集合进行增强,生成 2 张增强图像。这就是我们在单个训练批次中获得 2N 张图像的方式。

图 2:对比学习中的单个训练批次中的 6 张图像。每张图像下方的数字是该图像在输入批次中的索引,输入到对比学习模型中。图像来源:牛津视觉几何组(CC-SA)。
在接下来的章节中,我们将深入探讨 NT-Xent 损失的以下方面。
-
温度对 SoftMax 和 Sigmoid 的影响
-
NT-Xent 损失的简单直观解释
-
PyTorch 中 NT-Xent 的逐步实现
-
激发多标签损失函数需求(NT-BXent)
-
PyTorch 中 NT-BXent 的逐步实现
步骤 2-5 的所有代码可以在 这个笔记本 中找到。步骤 1 的代码可以在 这个笔记本 中找到。
温度对 SoftMax 和 Sigmoid 的影响
为了理解本文中要研究的对比损失函数的所有活动部分,我们需要首先了解温度对 SoftMax 和 Sigmoid 激活函数的影响。
通常,温度缩放应用于 SoftMax 或 Sigmoid 的输入,以平滑或突出这些激活函数的输出。在传递到激活函数之前,输入 logits 被温度除以。你可以在这个笔记本中找到所有相关代码。
SoftMax:对于 SoftMax,高温度会降低输出分布的方差,从而使标签变得更加柔和。低温度则会增加输出分布的方差,使最大值相对于其他值更加突出。请参见下面的图表,了解输入张量[0.1081, 0.4376, 0.7697, 0.1929, 0.3626, 2.8451]的温度对 SoftMax 的影响。

图 3:温度对 SoftMax 的影响。来源:作者
Sigmoid:对于 Sigmoid,高温度会导致输出分布向 0.0 拉伸,而低温度则将输入扩展到更高的值,使输出更接近 0.0 或 1.0,具体取决于输入的未签名幅度。
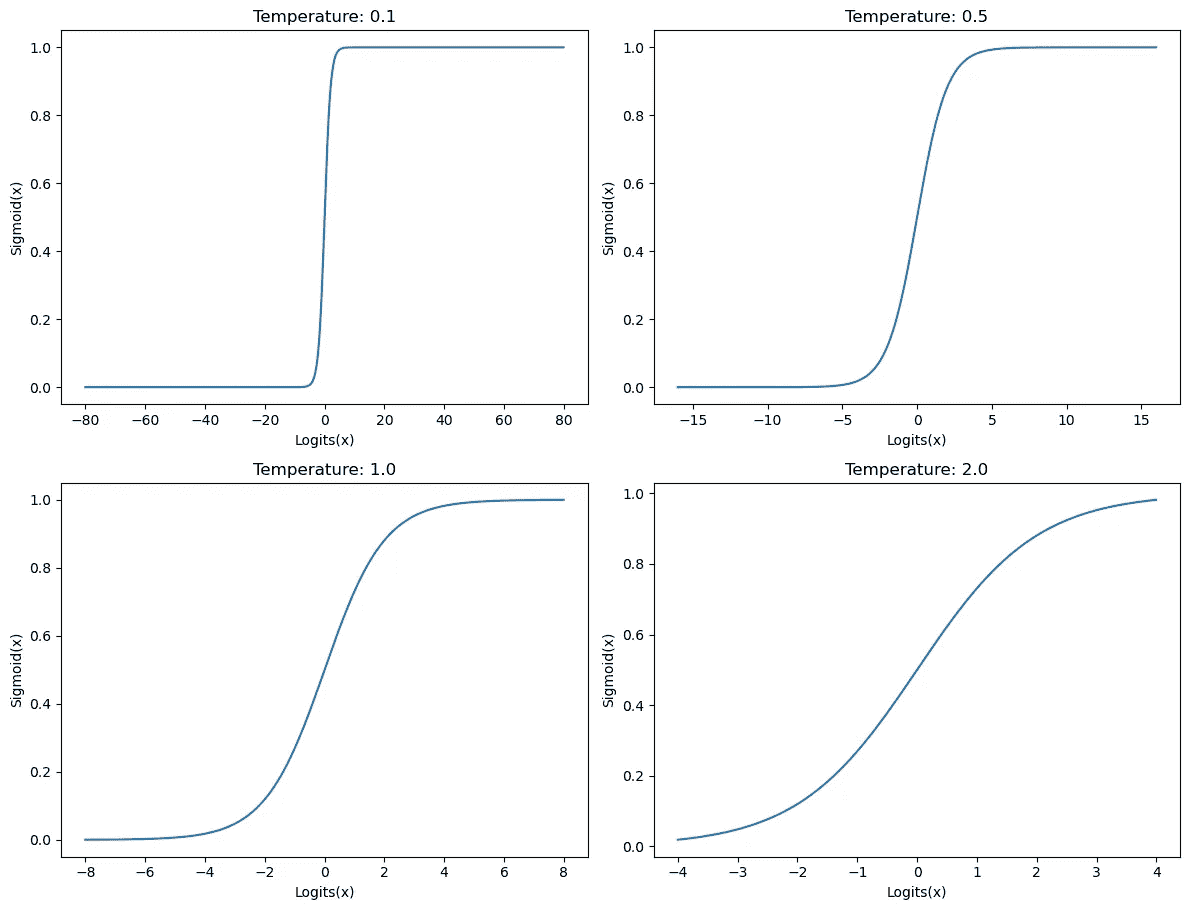
图 4:温度对 Sigmoid 的影响。来源:作者
现在我们理解了不同温度值对 SoftMax 和 Sigmoid 函数的影响,让我们看看这些知识如何应用于理解 NT-Xent 损失。
解读 NT-Xent 损失
NT-Xent 损失通过理解损失名称中的各个术语来进行理解。
-
标准化:余弦相似度产生范围在[-1.0 到+1.0]之间的标准化分数
-
温度缩放:所有对的余弦相似度在计算交叉熵损失之前被温度缩放
-
交叉熵损失:底层损失是一个多类别(单标签)交叉熵损失
如上所述,我们假设对于大小为 2N 的批次,以下索引处的特征向量代表正对(0, 1)、(2, 3)、(4, 5)、(6, 7)等,其余组合代表负对。在解释 NT-Xent 损失时,这一点是与 SimCLR 相关的重要因素。
现在我们了解了 NT-Xent 损失的术语在上下文中的含义,让我们来看看计算特征向量批次上 NT-Xent 损失所需的机械步骤。
-
所有对的余弦相似度分数是针对 SimCLR 模型生成的每个 2N 向量计算的。这导致了(2N)²的相似度分数,表示为一个 2N x 2N 矩阵
-
相同值 (i, i) 之间的比较结果会被丢弃(因为一个分布与自身完全相似,不能让模型学到任何有用的东西)
-
每个值(余弦相似度)都由温度参数 𝜏(这是一个超参数)进行缩放
-
交叉熵损失应用于上述结果矩阵的每一行。以下段落将详细解释
-
通常,这些损失的均值(每批次一个损失)用于反向传播
这里使用交叉熵损失的方式在语义上与标准分类任务中的使用方式略有不同。在分类任务中,训练一个最终的“分类头”来为每个输入产生一个独热概率向量,我们在这个独热概率向量上计算交叉熵损失,因为我们实际上是在计算两个分布之间的差异。这个视频 美丽地解释了交叉熵损失的概念。在 NT-Xent 损失中,训练层和输出分布之间没有一一对应的关系。相反,每个输入都计算一个特征向量,然后计算每对特征向量之间的余弦相似度。这里的诀窍是,由于每张图片与输入批次中的恰好 1 张其他图片相似(正样本对)(如果我们忽略特征向量与自身的相似度),我们可以将其视为一种类似分类的设置,其中图像之间相似度概率的概率分布表示了一个分类任务,其中一个值接近 1.0,其余值接近 0.0。
既然我们对 NT-Xent 损失有了充分的理解,我们应该能很好地将这些思想实现到 PyTorch 中。我们开始吧!
NT-Xent 损失在 PyTorch 中的实现
本节中的所有代码可以在这个笔记本中找到。
代码重用:许多NT-Xent 损失的实现从头开始实现所有操作。此外,其中一些实现损失函数的方式效率不高,更喜欢使用for 循环而非 GPU 并行。相反,我们将使用不同的方法。我们将通过 PyTorch 已经提供的标准交叉熵损失来实现这种损失。为此,我们需要将预测和真实标签转换为交叉熵可以接受的格式。下面我们来看一下如何实现。
预测张量:首先,我们需要创建一个 PyTorch 张量,它将表示我们对比学习模型的输出。假设我们的批量大小是 8(2N=8),并且我们的特征向量有 2 个维度(2 个值)。我们将输入变量称为 “x”。
x = torch.randn(8, 2)
余弦相似度:接下来,我们将计算此批次中每个特征向量之间的所有对的余弦相似度,并将结果存储在名为 “xcs” 的变量中。如果下面的代码看起来令人困惑,请阅读这个页面上的详细信息。这是“标准化”步骤。
xcs = F.cosine_similarity(x[None,:,:], x[:,None,:], dim=-1)
如上所述,我们需要忽略每个特征向量的自相似度分数,因为它不对模型的学习做出贡献,并且在我们想要计算交叉熵损失时会成为不必要的麻烦。为此,我们将定义一个变量 “eye”,这是一个矩阵,其中主对角线上的元素值为 1.0,其余元素值为 0.0。我们可以使用以下命令创建这样的矩阵。
eye = torch.eye(8)
现在让我们将其转换为布尔矩阵,以便可以使用这个掩码矩阵在 “xcs” 变量中进行索引。
eye = eye.bool()
让我们将张量 “xcs” 克隆到一个名为 “y” 的张量中,以便以后可以引用“xcs”张量。
y = xcs.clone()
现在,我们将所有对的余弦相似度矩阵的主对角线上的值设置为 -inf,这样当我们对每一行计算 softmax 时,这个值将不会产生任何贡献。
y[eye] = float("-inf")
张量 “y” 通过温度参数缩放后,将成为 PyTorch 中的交叉熵损失 API 的输入之一。接下来,我们需要计算要传递给交叉熵损失 API 的真实标签(目标)。
真实标签(目标张量):对于我们使用的示例(2N=8),这就是真实标签张量的样子。
tensor([1, 0, 3, 2, 5, 4, 7, 6])
这是因为张量 “y” 中的以下索引对包含正对。
(0, 1), (1, 0)
(2, 3), (3, 2)
(4, 5), (5, 4)
(6, 7), (7, 6)
要解释上述索引对,我们来看一个单一的例子。对 (4, 5) 来说,这意味着第 4 行第 5 列应该设置为 1.0(正对),这也是上述张量所表示的。太好了!
要创建上述张量,我们可以使用以下 PyTorch 代码,该代码将真实标签存储在变量 “target” 中。
target = torch.arange(8)
target[0::2] += 1
target[1::2] -= 1
交叉熵损失:我们已经具备了计算损失所需的所有成分!剩下的唯一任务就是调用 PyTorch 中的 cross_entropy API。
loss = F.cross_entropy(y / temperature, target, reduction="mean")
变量 “loss” 现在包含了计算出的 NT-Xent 损失。让我们把所有的代码封装到一个 Python 函数中。
def nt_xent_loss(x, temperature):
assert len(x.size()) == 2
# Cosine similarity
xcs = F.cosine_similarity(x[None,:,:], x[:,None,:], dim=-1)
xcs[torch.eye(x.size(0)).bool()] = float("-inf")
# Ground truth labels
target = torch.arange(8)
target[0::2] += 1
target[1::2] -= 1
# Standard cross-entropy loss
return F.cross_entropy(xcs / temperature, target, reduction="mean")
上述代码有效,只要每个特征向量在训练对比学习模型时批次中恰好有一个正对。让我们来看一下如何在对比学习任务中处理多个正对。
用于对比学习的多标签损失:NT-BXent
在 SimCLR 论文中,每个图像i在索引j处有恰好 1 个相似对。这使得交叉熵损失成为任务的完美选择,因为它类似于多类别问题。相反,如果我们将 M > 2 个相同图像的增强输入到对比学习模型的单个训练批次中,那么每个批次将包含图像i的 M-1 个相似对。这将使任务类似于多标签问题。
显而易见的选择是将交叉熵损失替换为二元交叉熵损失。因此命名为 NT-BXent 损失,代表归一化温度缩放的二元交叉熵损失。
下面的公式展示了元素i的损失Li。公式中的σ表示S 型函数。
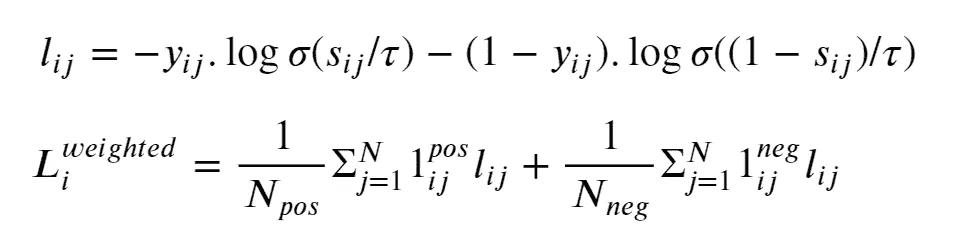
图 5:NT-BXent 损失的公式。图像来源:本文作者
为了避免类别不平衡问题,我们通过我们小批量中正负对的数量的倒数来加权正负对。在用于反向传播的小批量中的最终损失将是小批量中每个样本损失的平均值。
接下来,让我们将注意力集中在我们在 PyTorch 中对 NT-BXent 损失的实现上。
在 PyTorch 中实现 NT-BXent 损失
本节中的所有代码可以在这个笔记本中找到。
代码重用:类似于我们对 NT-Xent 损失的实现,我们将重用 PyTorch 提供的二元交叉熵(BCE)损失方法。我们的真实标签设置将类似于使用 BCE 损失的多标签分类问题。
预测张量:我们将使用与 NT-Xent 损失实现中相同的(8, 2)预测张量。
x = torch.randn(8, 2)
余弦相似度:由于输入张量x相同,所有对的余弦相似度张量xcs也将相同。有关下面这行代码的详细解释,请参见这一页。
xcs = F.cosine_similarity(x[None,:,:], x[:,None,:], dim=-1)
为了确保位置***(i, i)处的损失为0***,我们需要进行一些操作,使得在对xcs张量应用 Sigmoid 后,它在每个索引***(i, i)处的值为1***。由于我们将使用 BCE 损失,我们会将每个特征向量的自相似性分数标记为张量xcs中的值为无穷大。这是因为在xcs张量上应用 Sigmoid 函数将无穷大转换为值1,我们将设置我们的真实标签,使得真实标签中的每个位置***(i, i)的值为1***。
创建一个掩码张量,该张量在主对角线上具有值True(xcs在主对角线上具有自相似性分数),而其他地方为False。
eye = torch.eye(8).bool()
将张量*“xcs”克隆到一个名为“y”的张量中,以便我们可以稍后引用“xcs”*张量。
y = xcs.clone()
现在,我们将所有对的余弦相似度矩阵的主对角线上的值设置为无穷大,以便在对每一行计算 Sigmoid 时,这些位置的值为 1。
y[eye] = float("inf")
张量*“y”*由温度参数缩放后,将作为 PyTorch 中BCE 损失 API的输入(预测)之一。接下来,我们需要计算要提供给 BCE 损失 API 的真实标签(目标)。
真实标签(目标张量):我们期望用户传递给我们包含正例的所有(x, y)索引对。这与我们对 NT-Xent 损失所做的有所不同,因为正对是隐式的,而这里正对是显式的。
除了用户提供的位置外,我们还将所有对角线元素设置为正对,如上所述。我们将使用 PyTorch 张量索引 API 提取这些位置的所有元素并将其设置为 1,而其他元素初始化为 0。
target = torch.zeros(8, 8)
pos_indices = torch.tensor([
(0, 0), (0, 2), (0, 4),
(1, 4), (1, 6), (1, 1),
(2, 3),
(3, 7),
(4, 3),
(7, 6),
])
# Add indexes of the principal diagonal as positive indexes.
# This will be useful since we will use the BCELoss in PyTorch,
# which will expect a value for the elements on the principal
# diagonal as well.
pos_indices = torch.cat([pos_indices, torch.arange(8).reshape(8, 1).expand(-1, 2)], dim=0)
# Set the values in the target vector to 1.
target[pos_indices[:,0], pos_indices[:,1]] = 1
二元交叉熵(BCE)损失:与 NT-Xent 损失不同,我们不能简单调用torch.nn.functional.binary_cross_entropy_function,因为我们需要根据当前小批量中索引 i 处的正负对数目来加权正负损失。
不过第一步是计算逐元素的 BCE 损失。
temperature = 0.1
loss = F.binary_cross_entropy((y / temperature).sigmoid(), target, reduction="none")
我们将创建一个正负对的二进制掩码,然后创建两个张量,loss_pos 和 loss_neg,只包含计算损失中对应于正对和负对的元素。
target_pos = target.bool()
target_neg = ~target_pos
# loss_pos and loss_neg below contain non-zero values only for those elements
# that are positive pairs and negative pairs respectively.
loss_pos = torch.zeros(x.size(0), x.size(0)).masked_scatter(target_pos, loss[target_pos])
loss_neg = torch.zeros(x.size(0), x.size(0)).masked_scatter(target_neg, loss[target_neg])
接下来,我们将分别对每个小批量中的元素 i 的正负对损失进行求和。
# loss_pos and loss_neg now contain the sum of positive and negative pair losses
# as computed relative to the i'th input.
loss_pos = loss_pos.sum(dim=1)
loss_neg = loss_neg.sum(dim=1)
为了进行加权,我们需要跟踪每个小批量中每个元素 i 对应的正负对的数量。张量*“num_pos”和“num_neg”*将存储这些值。
# num_pos and num_neg below contain the number of positive and negative pairs
# computed relative to the i'th input. In an actual setting, this number should
# be the same for every input element, but we let it vary here for maximum
# flexibility.
num_pos = target.sum(dim=1)
num_neg = target.size(0) - num_pos
我们已经具备了计算损失所需的所有要素!我们唯一需要做的就是按正负对的数量对正负损失进行加权,然后在小批量中计算损失的平均值。
def nt_bxent_loss(x, pos_indices, temperature):
assert len(x.size()) == 2
# Add indexes of the principal diagonal elements to pos_indices
pos_indices = torch.cat([
pos_indices,
torch.arange(x.size(0)).reshape(x.size(0), 1).expand(-1, 2),
], dim=0)
# Ground truth labels
target = torch.zeros(x.size(0), x.size(0))
target[pos_indices[:,0], pos_indices[:,1]] = 1.0
# Cosine similarity
xcs = F.cosine_similarity(x[None,:,:], x[:,None,:], dim=-1)
# Set logit of diagonal element to "inf" signifying complete
# correlation. sigmoid(inf) = 1.0 so this will work out nicely
# when computing the Binary cross-entropy Loss.
xcs[torch.eye(x.size(0)).bool()] = float("inf")
# Standard binary cross-entropy loss. We use binary_cross_entropy() here and not
# binary_cross_entropy_with_logits() because of
# https://github.com/pytorch/pytorch/issues/102894
# The method *_with_logits() uses the log-sum-exp-trick, which causes inf and -inf values
# to result in a NaN result.
loss = F.binary_cross_entropy((xcs / temperature).sigmoid(), target, reduction="none")
target_pos = target.bool()
target_neg = ~target_pos
loss_pos = torch.zeros(x.size(0), x.size(0)).masked_scatter(target_pos, loss[target_pos])
loss_neg = torch.zeros(x.size(0), x.size(0)).masked_scatter(target_neg, loss[target_neg])
loss_pos = loss_pos.sum(dim=1)
loss_neg = loss_neg.sum(dim=1)
num_pos = target.sum(dim=1)
num_neg = x.size(0) - num_pos
return ((loss_pos / num_pos) + (loss_neg / num_neg)).mean()
pos_indices = torch.tensor([
(0, 0), (0, 2), (0, 4),
(1, 4), (1, 6), (1, 1),
(2, 3),
(3, 7),
(4, 3),
(7, 6),
])
for t in (0.01, 0.1, 1.0, 10.0, 20.0):
print(f"Temperature: {t:5.2f}, Loss: {nt_bxent_loss(x, pos_indices, temperature=t)}")
打印。
温度:0.01,损失:62.898780822753906
温度:0.10,损失:4.851151943206787
温度:1.00,损失:1.0727109909057617
温度:10.00,损失:0.9827173948287964
温度:20.00,损失:0.982099175453186
结论
自监督学习是深度学习中的一个新兴领域,它允许在未标记的数据上训练模型。这项技术让我们绕过了大规模标记数据的需求。
在这篇文章中,我们了解了对比学习的损失函数。第一个,称为 NT-Xent 损失,用于对每个输入在小批量中学习单个正对。我们介绍了 NT-BXent 损失,该损失用于在小批量中对每个输入学习多个(> 1)正对。我们学会了直观地解释这些损失,基于我们对交叉熵损失和二元交叉熵损失的理解。最后,我们在 PyTorch 中高效地实现了这两种损失函数。
NumPy 广播
定义、规则和示例
·
关注 发表在 Towards Data Science ·9 分钟阅读·2023 年 1 月 4 日
–
摄影:Jean-Guy Nakars 摄于 Unsplash
介绍
NumPy 提供了通过矢量化进行快速计算的方法,这避免了使用较慢的 Python 循环。矢量化在使用二元 ufuncs(如加法或乘法)时也可用,附加的好处是数组不需要具有相同的形状。具有不同形状的数组之间的操作称为 广播,这可能会特别令人困惑,特别是对于多维数组,或当两个数组都需要扩展时。
有许多示例和教程,但我发现通过思考并实际记住广播规则来处理问题最有用。这样更容易考虑任何给定的使用案例,并编写代码,而无需依赖试错法。
广播规则
我强烈推荐两本数据分析和数据科学的书籍。它们都有关于广播的小节。
数据分析的 Python 由 Wes McKinney 编写,包含以下广播规则:
如果对于每个尾部维度(即从末尾开始)轴长度匹配,或者任一长度为 1,则两个数组可以进行广播。广播将对缺失或长度为 1 的维度进行。
Python 数据科学手册 由 Jake VanderPlas 编写,包含更详细的广播规则:
规则 1:如果两个数组在维度数量上不同,维度较少的那个数组的形状会在其前面(左侧)用 1 进行填充。
规则 2:如果两个数组的形状在任何维度上不匹配,则形状为 1 的数组会被扩展以匹配另一个形状。
规则 3:如果在任何维度上大小不一致且都不等于 1,将会引发错误。
我发现第二组规则更容易遵循。下面的示例将使用这些规则。
示例
可能最简单的广播示例之一,以及一个典型模式,是从每一列中减去列均值。进行此操作后,列均值将变为数值上等于零。
a = np.arange(12).reshape(4, 3)
means_columns = a.mean(axis=0)
res = a - means_columns
print('original array', a, sep='\n')
print('.. column means', a.mean(axis=0), sep='\n')
print('demeaned array', res, sep='\n')
print('.. column means', res.mean(axis=0), sep='\n')
这会打印
original array
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
.. column means
[4.5 5.5 6.5]
demeaned array
[[-4.5 -4.5 -4.5]
[-1.5 -1.5 -1.5]
[ 1.5 1.5 1.5]
[ 4.5 4.5 4.5]]
.. column means
[0\. 0\. 0.]
让我们看看这里发生了什么。计算 a.mean(axis=0) 的列均值会生成一个形状为 (3,) 的一维数组。涉及减法的两个数组在形状上有所不同,因此 means_columns 会根据规则 1 在左侧填充 1 以匹配形状。因此,在幕后,means_columns 会被重塑为 (1, 3)。然后根据规则 2,means_columns 会沿着轴 0 扩展,使其形状变为 (3, 3) 以匹配 a 的形状。
除了使用规则预测维度较少的数组如何被扩展外,我们还可以使用 [np.broadcast_to](https://numpy.org/doc/stable/reference/generated/numpy.broadcast_to.html),它返回一个只读视图,该视图具有给定的形状。该视图可能是不连续的,且不同元素可能指向相同的内存地址。
means_columns_bc = np.broadcast_to(means_columns, a.shape)
print(means_columns_bc)
print('base', means_columns_bc.base, sep='\n')
print('strides', means_columns_bc.strides, sep='\n')
这会打印
[[4.5 5.5 6.5]
[4.5 5.5 6.5]
[4.5 5.5 6.5]
[4.5 5.5 6.5]]
base
[4.5 5.5 6.5]
strides
(0, 8)
我们可以看到基础是原始的均值数组(因此它是一个视图),而沿第一个轴的步幅是 0,这意味着同一列的不同元素指向相同的内存位置(有关 NumPy 内部的介绍,请参见这里)。NumPy 确实在尽可能优化内存使用!
如果我们想对行进行去均值操作怎么办?可以通过a.mean(axis=1)快速计算行的均值,该操作将返回一个形状为(4,)的数组。将其形状左侧填充 1,意味着数组将变成(1,4)。根据规则 3,这两个数组的最后维度不一致且都不是 1。这意味着广播不会发生。我们也可以预见到这一点,因为np.broadcast_to(a.mean(axis=1), a.shape)引发异常,告知我们广播无法生成请求的形状(4, 3)。形状的不兼容性还可以通过执行np.broadcast_shapes(a.shape, a.mean(axis=1).shape)来观察,这也引发异常,解释了形状不匹配。通过将行均值重塑为(4,1)数组来进行行去均值操作,可以使用a.mean(axis=1).reshape(-1, 1)或a.mean(axis=1)[:, np.newaxis]
means_rows = a.mean(axis=1)
res = a - means_rows.reshape(-1, 1) # or res = a - means_rows[:, np.newaxis]
print('original array', a, sep='\n')
print('.. row means', a.mean(axis=1), sep='\n')
print('demeaned array', res, sep='\n')
print('.. row means', res.mean(axis=1), sep='\n')
这将打印
original array
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
.. row means
[ 1\. 4\. 7\. 10.]
demeaned array
[[-1\. 0\. 1.]
[-1\. 0\. 1.]
[-1\. 0\. 1.]
[-1\. 0\. 1.]]
.. row means
[0\. 0\. 0\. 0.]
规则 2 清楚地解释了为什么这有效,因为形状为(4,1)的数组可以在列中扩展,使其形状变成(4,3)。
在第三个示例中,我们将演示广播如何在 ufunc 二元函数中扩展两个数组
a = np.arange(4)
b = np.arange(3)
res = a[:, np.newaxis] + b[np.newaxis, :]
print('result array', res, sep='\n')
这将得到
result array
[[0 1 2]
[1 2 3]
[2 3 4]
[3 4 5]]
严格来说,重塑b并不是必要的,但它使事情更清晰。我们还可以使用[np.broadcast_arrays](https://numpy.org/doc/stable/reference/generated/numpy.broadcast_arrays.html)或相关且更灵活的[np.broadcast](https://numpy.org/doc/stable/reference/generated/numpy.broadcast.html#numpy.broadcast)来广播两个数组,而不应用 ufunc。为了完整起见,还有其他方法可以实现与广播相同的结果,一个例子是np.add.outer(a, b),它产生与
np.array_equal(np.add.outer(a, b), a[:, np.newaxis] + b)
返回 True。
对任何轴上的高维数组进行去均值操作可以被推广为
def demean_axis(arr, axis=1):
means = arr.mean(axis)
indexer = [slice(None)]*arr.ndim
indexer[axis] = np.newaxis
return arr - means[tuple(indexer)]
arr = np.linspace(1, 12, 24*3).reshape(6,4,3)
res = demean_axis(arr, axis=1)
我们可以确认np.abs(res.mean(axis=1)).max()在数值上等于零。上述函数取自 Wes McKinney 的书籍,但需要稍微修改以适配本文使用的 NumPy 版本(1.23.4)。
作为一个更实际的例子,我们可以使用广播将彩色图像转换为灰度图像。广播部分已用注释标出:
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt
import io
import numpy as np
from PIL import Image
# read in the original image (png)
with open('landscape_water_lake_nature_trees.png', mode='rb') as f:
image_orig = f.read()
f = io.BytesIO(image_orig)
im = Image.open(f)
image_orig = np.array(im)/255.
print('shape of original image', image_orig.shape, sep='\n')
# convert RGBA to RGB (pillow could be used for this)
background = (1., 1., 1.)
row = image_orig.shape[0]
col = image_orig.shape[1]
image_color = np.zeros( (row, col, 3), dtype='float32' )
r, g, b, a = image_orig[:,:,0], image_orig[:,:,1], image_orig[:,:,2], image_orig[:,:,3]
a = np.asarray( a, dtype='float32' )
R, G, B = background
image_color[:,:,0] = r * a + (1.0 - a) * R
image_color[:,:,1] = g * a + (1.0 - a) * G
image_color[:,:,2] = b * a + (1.0 - a) * B
print('shape of image after RGBA to RGB conversion', image_color.shape, sep='\n')
# convert to greyscale
conv = np.array([0.2126, 0.7152, 0.0722])
# --- broadcasting !!! ---
image_grey = (image_color[:,:,:3]*conv).sum(axis=2)
# --- broadcasting !!! ---
print('shape of image after conversion to greyscale', image_grey.shape, sep='\n')
# plot the image
fig = plt.figure(figsize=(8, 4))
axs = fig.subplots(1, 2)
axs[0].axis('off')
axs[0].set_title('RGB image')
axs[0].imshow(image_color)
axs[1].axis('off')
axs[1].set_title('greyscale image')
axs[1].imshow(image_grey, cmap='gray')
axs[0].annotate('',xy=(0.52,0.5),xytext=(0.50,0.5),arrowprops=dict(facecolor='black'),
xycoords='figure fraction', textcoords='figure fraction')
fig.savefig('RGBA_to_greyscale.png')
上述代码生成

将透明 PNG 图像转换为灰度图像(照片由nextvoyage在pixabay提供)
也许值得关注的是,原图是一个 RGBA 图像(红色、绿色、蓝色、透明度),即它还包含第四个 alpha 通道来指示每个像素的透明度。我们通过使用白色背景将 RGBA 图像转换为 RGB。这以及示例中的几乎所有内容,都可以使用Pillow来完成,但我们故意尽可能使用 NumPy(例如,Pillow 可以转换为灰度图像以保持透明度)。代码的最后部分是一些Matplotlib的花招,用于比较彩色图像和灰度图像。
转换为灰度图像是通过以下公式完成的。
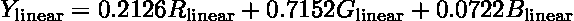
来自维基百科的this page。执行乘法和求和的代码部分,将图像数组的形状从(1080,1920,3)更改为(1080,1920)的部分已被注释掉。你可能会想,为了一行广播代码展示如此长的示例是否值得。这正是要点!广播是简洁的,如果没有它,代码会更长且更慢。通常,算法背后的魔法是几行 NumPy 操作,通常包括广播。
设置值
大多数 NumPy 用户将广播与数组加法或乘法相关联。然而,当使用索引设置值时,广播同样适用。下面你可以找到一组示例,我们将不对其详细评论。
# set one row, same value to all columns
a = np.ones((4,3))
a[0] = -1
# array([[-1., -1., -1.],
# [ 1., 1., 1.],
# [ 1., 1., 1.],
# [ 1., 1., 1.]])
# set one column, same value to all rows
a = np.ones((4,3))
a[:, 0] = -1
# array([[-1., 1., 1.],
# [-1., 1., 1.],
# [-1., 1., 1.],
# [-1., 1., 1.]])
# set all rows, same value to all elements
a = np.ones((4,3))
a[:] = -1
# array([[-1., -1., -1.],
# [-1., -1., -1.],
# [-1., -1., -1.],
# [-1., -1., -1.]])
# set all rows, different value to each column
a = np.ones((4,3))
b = np.array([-1, -2, -3])
a[:] = b
# array([[-1., -2., -3.],
# [-1., -2., -3.],
# [-1., -2., -3.],
# [-1., -2., -3.]])
# set all rows, different value to each row
a = np.ones((4,3))
b = np.array([-1, -2, -3, -4])
b = b[:, np.newaxis]
a[:] = b
# array([[-1., -1., -1.],
# [-2., -2., -2.],
# [-3., -3., -3.],
# [-4., -4., -4.]])
# set some rows, different value to each column
a = np.ones((4,3))
b = np.array([-1, -2, -3])
a[:3] = b
# array([[-1., -2., -3.],
# [-1., -2., -3.],
# [-1., -2., -3.],
# [ 1., 1., 1.]])
# set some rows, different value to each row
a = np.ones((4,3))
b = np.array([-1, -2, -3])
a[:3] = b[:, np.newaxis]
# array([[-1., -1., -1.],
# [-2., -2., -2.],
# [-3., -3., -3.],
# [ 1., 1., 1.]])
# set some columns, different value to each column
a = np.ones((4,3))
b = np.array([-1, -2])
a[:,:2] = b
# array([[-1., -2., 1.],
# [-1., -2., 1.],
# [-1., -2., 1.],
# [-1., -2., 1.]])
# set some columns, different value to each row
a = np.ones((4,3))
b = np.array([-1, -2, -3, -4])
a[:,:2] = b[:, np.newaxis]
# array([[-1., -1., 1.],
# [-2., -2., 1.],
# [-3., -3., 1.],
# [-4., -4., 1.]])
结论
广播可能看起来很复杂,但如果记住几个关键原则,它可以很容易掌握。最重要的原则是数组的形状从右开始对齐。缺失的维度用一填充,始终在左侧。通过扩展维度为一的形状,这两个形状变得相同。在两个(或更多!)数组可以进行广播之前,可能需要使用np.newaxis进行一些重新形状调整。广播不仅用于计算整个数组,还用于设置数组中的某些值。这就是要点。通过一些练习,NumPy 的广播可以导致令人惊讶的简洁和高效的代码。充分利用它的潜力!
探究字符级 RNN:基于 NumPy 的实现指南
由于最近 LLMs 蓬勃发展,掌握语言建模的基础知识至关重要
 ](https://sassonjoe66.medium.com/?source=post_page-----af1428bb10a8--------------------------------)
](https://sassonjoe66.medium.com/?source=post_page-----af1428bb10a8--------------------------------) ](https://towardsdatascience.com/?source=post_page-----af1428bb10a8--------------------------------) Joe Sasson
](https://towardsdatascience.com/?source=post_page-----af1428bb10a8--------------------------------) Joe Sasson
·
关注 发表在 Towards Data Science ·17 min read·Jan 27, 2023
–
图片来自 Markus Spiske on Unsplash
简介
循环神经网络(RNNs)是一种强大的神经网络类型,能够处理序列数据,如时间序列或自然语言。本文将通过使用 NumPy 从零开始构建一个 Vanilla RNN 的过程。我们将首先讨论 RNN 的理论和直觉,包括它们的架构和适合解决的问题类型。接下来,我们将深入代码,解释 RNN 的各个组件及其相互作用。最后,我们将通过将 RNN 应用于实际数据集来展示其有效性。
具体来说,我们将实现一个多对多的字符级 RNN,使用序列化的在线学习。这意味着网络一次处理一个字符的输入序列,并在每个字符后更新网络参数。这允许网络在实时学习,并随着遇到的新模式而适应数据。
字符级 RNN 意味着输入和输出是单个字符,而不是单词或句子。这使得网络能够学习文本中字符之间的潜在模式和依赖关系。多对多架构指的是网络接收一个字符序列作为输入,并生成一个字符序列作为输出。这与多对一架构不同,在多对一架构中,网络接收一个输入序列并生成一个输出,或者与一对多架构不同,在一对多架构中,网络接收一个输入并生成一个输出序列。
我使用了 Andrej Karpathy 的代码(见这里)作为我的实现基础,并做了几处修改以提高通用性和可靠性。我扩展了代码以支持多个层次,并重新构建了它以提高可读性和重用性。这个项目建立在我之前使用 NumPy 创建简单 ANN 的工作基础上。相关源代码可以在这里找到。
理论与直觉
RNNs 可以与传统的前馈神经网络(ANNs)对比,后者没有“记忆”机制,并且独立处理每个输入。ANNs 适用于输入和输出具有固定大小且输入不包含序列依赖关系的问题。相比之下,RNNs 能够处理变长的输入序列,并通过隐藏状态保持对过去输入的“记忆”。
隐藏状态使 RNN 能够捕捉时间依赖关系,并根据整个输入序列做出预测。总的来说,网络使用来自先前时间步的信息来指导其对当前输入的处理。此外,更复杂的 NLP 架构可以处理长期依赖关系(GPT-3 使用了 2048 的序列长度进行训练),其中输入序列开头的信息对于预测序列末尾的输出仍然相关。这种保持“记忆”的能力使 RNN 和变换器在处理序列数据时相较于 ANNs 具有显著优势。
最近,像GPT-3和BERT这样的变换器架构在各种 NLP 任务中变得越来越流行。这些架构基于自注意力机制,使网络能够有选择地关注输入序列的不同部分。这使得网络能够捕捉长期依赖关系,而无需递归,从而比 RNN 更高效且更易于训练。变换器架构已在各种 NLP 任务中实现了最先进的结果,并被用于许多实际应用中。
尽管变换器架构比普通 RNN 更复杂且具有不同的特性,但普通 RNN 在深度学习领域仍然发挥着重要作用。它们易于理解,容易实现和调试,并可以作为其他更复杂架构的构建块。在本文中,我们将重点关注普通 RNN,并窥探其真正的工作原理。
普通 RNN 的三种主要类型是:
-
一对多: 输入一张狗的图片并输出‘狗的图片’
-
多对一: 输入一个句子并接收情感(情感分析)
-
多对多: 输入一个句子并输出完整句子(见下文)
我们将实现如下所示的多对多架构。
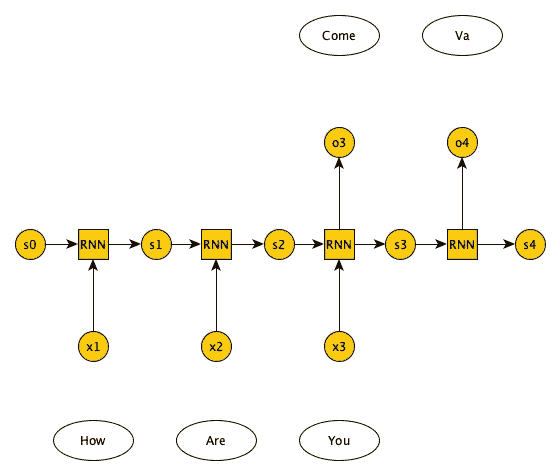
来源: Kaivan Kamali,《深度学习(第二部分)——递归神经网络(RNN)》(银河培训材料)。training.galaxyproject.org/training-material/topics/statistics/tutorials/RNN/tutorial.html
从这一点开始,我们将使用h[t]表示时间步 t 的隐藏状态。在图中,这被表示为s[t]。
如你所见,来自上一个时间步的隐藏状态h[t-1]与当前输入x[t]结合,这一过程在时间步数上重复。在 RNN 块内,我们正在更新当前时间步的隐藏状态。
为了澄清,时间步只是一个字符,如 ‘a’ 或 ‘d’。输入序列包含一个可变数量的字符或时间步,也称为序列长度,这是网络的一个超参数。
代码
目录
-
准备数据
-
RNN 类
-
前向传播
-
反向传播
-
优化器
-
训练
准备数据
## start with data
data = open('path-to-data', 'r').read() # should be simple plain text file
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print('data has {} characters, {} unique.'.format(data_size, vocab_size))
char_to_idx = { ch:i for i,ch in enumerate(chars) }
idx_to_char = { i:ch for i,ch in enumerate(chars) }
我们从一个纯文本文件中读取数据作为字符串,并对字符进行标记化。每个唯一字符(共 65 个)将映射到一个整数,反之亦然。
让我们为 RNN 采样一个输入和目标序列。
pointer, seq_length = 0, 8
x = [char_to_idx[ch] for ch in data[pointer:pointer+seq_length]]
y = [char_to_idx[ch] for ch in data[pointer+1:pointer+seq_length+1]]
print(x)
>> [2, 54, 53, 62, 13, 28, 20, 54] # our RNN input sequence
print(y)
>> [54, 53, 62, 13, 28, 20, 54, 13] # our RNN target sequence
for t in range(seq_length):
context = x[:t+1]
target = y[t]
print(f"when input is {context} the target: {target}")
>> when input is [2] the target: 54
when input is [2, 54] the target: 53
when input is [2, 54, 53] the target: 62
when input is [2, 54, 53, 62] the target: 13
when input is [2, 54, 53, 62, 13] the target: 28
when input is [2, 54, 53, 62, 13, 28] the target: 20
when input is [2, 54, 53, 62, 13, 28, 20] the target: 54
when input is [2, 54, 53, 62, 13, 28, 20, 54] the target: 13
输入是一个标记化的序列,目标是输入偏移一个单位后的值。
RNN 类
class RNN:
def __init__(self, hidden_size, vocab_size, seq_length, num_layers):
pass
def __call__(self, *args: Any, **kwds: Any):
"""RNN Forward Pass"""
pass
def backward(self, targets, cache):
"""RNN Backward Pass"""
pass
def update(self, grads, lr):
"""Perform Parameter Update w/ Adagrad"""
pass
def predict(self, hprev, seed_ix, n):
"""
Make predictions using the trained RNN model.
Parameters:
hprev (numpy array): The previous hidden state.
seed_ix (int): The seed letter index to start the prediction with.
n (int): The number of characters to generate for the prediction.
Returns:
ixes (list): The list of predicted character indices.
hs (numpy array): The final hidden state after making the predictions.
"""
pass
让我们开始讨论 RNN 的组件,与基本 ANN 相比。
在传统的前馈神经网络中,控制层间交互的参数由一个单一的权重矩阵表示,记作 W。然而,在递归神经网络(RNN)中,层间交互由多个矩阵表示。在我的代码中,这些矩阵特别是:Wxh、Whh 和 Why,分别表示输入层与隐藏层、隐藏层与隐藏层、以及隐藏层与输出层之间的权重。
Wxh 矩阵将输入层连接到隐藏层,并用于将每个时间步的输入转换为隐藏层的激活值。Whh 矩阵将时间步 t-1 的隐藏层连接到时间步 t 的隐藏层,并用于将隐藏状态从一个时间步传播到下一个时间步。Why 矩阵将隐藏层连接到输出层,并用于将隐藏状态转换为网络的最终输出。
总之,ANN 和 RNN 之间的主要区别在于 ANN 有一个权重矩阵,而 RNN 有多个权重矩阵,这些矩阵用于转换输入、传播隐藏状态并生成最终输出。这些多个权重矩阵使 RNN 能够保持对过去输入的记忆,并在时间上移动信息。
构造函数
def __init__(self, hidden_size, vocab_size, seq_length, num_layers):
self.name = 'RNN'
self.hidden_size = hidden_size
self.vocab_size = vocab_size
self.num_layers = num_layers
# model parameters
self.Wxh = [np.random.randn(hidden_size, vocab_size)*0.01 for _ in range(num_layers)] # input to hidden
self.Whh = [np.random.randn(hidden_size, hidden_size)*0.01 for _ in range(num_layers)] # hidden to hidden
self.Why = np.random.randn(vocab_size, hidden_size)*0.01 # hidden to output
self.bh = [np.zeros((hidden_size, 1)) for _ in range(num_layers)] # hidden bias
self.by = np.zeros((vocab_size, 1)) # output bias
# memory variables for training (ada grad from karpathy's github)
self.iteration, self.pointer = 0, 0
self.mWxh = [np.zeros_like(w) for w in self.Wxh]
self.mWhh = [np.zeros_like(w) for w in self.Whh]
self.mWhy = np.zeros_like(self.Why)
self.mbh, self.mby = [np.zeros_like(b) for b in self.bh], np.zeros_like(self.by)
self.loss = -np.log(1.0/vocab_size)*seq_length # loss at iteration 0
self.running_loss = []
在这里,我们定义了如上所述的 RNN 参数。值得注意的是——参数 Why 和 by 表示一个线性层,甚至可以进一步抽象为一个独立的类,如 PyTorch 的 ‘nn.Linear’ 模块。然而,在此实现中,我们将它们作为 RNN 类的一部分保留。
前向传播
def __call__(self, *args: Any, **kwds: Any) -> Any:
"""RNN Forward Pass"""
x, y, hprev = kwds['inputs'], kwds['targets'], kwds['hprev']
loss = 0
xs, hs, ys, ps = {}, {}, {}, {} # inputs, hidden state, output, probabilities
hs[-1] = np.copy(hprev)
# forward pass
for t in range(len(x)):
xs[t] = np.zeros((self.vocab_size,1)) # encode in 1-of-k representation
xs[t][x[t]] = 1
hs[t] = np.copy(hprev)
if kwds.get('dropout', False): # use dropout layer (mask)
for l in range(self.num_layers):
dropout_mask = (np.random.rand(*hs[t-1][l].shape) < (1-0.5)).astype(float)
hs[t-1][l] *= dropout_mask
hs[t][l] = np.tanh(np.dot(self.Wxh[l], xs[t]) + np.dot(self.Whh[l], hs[t-1][l]) + self.bh[l]) # hidden state
hs[t][l] = hs[t][l] / (1 - 0.5)
else: # no dropout layer (mask)
for l in range(self.num_layers):
hs[t][l] = np.tanh(np.dot(self.Wxh[l], xs[t]) + np.dot(self.Whh[l], hs[t-1][l]) + self.bh[l]) # hidden state
ys[t] = np.dot(self.Why, hs[t][-1]) + self.by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
loss += -np.log(ps[t][y[t],0]) # softmax (cross-entropy loss)
self.running_loss.append(loss)
return loss, hs[len(x)-1], {'xs':xs, 'hs':hs, 'ps':ps}
从顶部开始,逐步解析。这儿发生了什么?
循环外,每个序列一次
-
hprev 是我们的初始隐藏状态
-
我们正在初始化字典以保存我们的输入、隐藏状态、logits 和概率。我们将在反向传播过程中需要这些。
-
我们将损失初始化为零。
-
我们将初始隐藏状态
hprev设置为hs[-1](表示时间步 t-1)。
循环内,每个时间步
-
对我们的输入序列进行独热编码
-
在时间步‘t’和层‘l’更新隐藏状态。
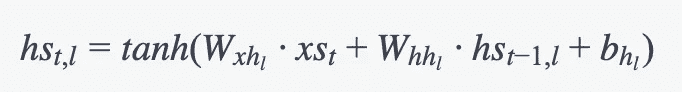
我们隐藏状态的数学表示。图片由作者提供。
- 此外,你可能注意到有一些功能用于执行dropout。
Dropout 是一种正则化技术,旨在通过在训练过程中随机“丢弃”(置为零)某些神经元来防止过拟合。在上述代码中,dropout 层在更新时间步‘t’、层‘l’的隐藏状态之前应用,通过将时间步‘t-1’的隐藏状态与 dropout 掩码相乘来实现。dropout 掩码是通过创建一个二值掩码生成的,其中每个元素以概率 p 为 1,否则为 0。通过这样做,我们在隐藏状态中随机“丢弃”一定数量的神经元,这有助于防止网络对任何单一神经元过于依赖。这使得网络更为鲁棒,并且不容易在训练数据上过拟合。在应用 dropout 之后,通过将隐藏状态除以(1-p)来缩放隐藏状态,以确保隐藏状态的期望值得到保持。
-
ys[t]为当前时间步提供线性层的输出。 -
ps[t]为当前时间步提供最终的 softmax 输出(概率)。
由于只有一层线性层,而不是任意数量的 RNN 层,因此ys[t]和ps[t]的计算位于第二个循环之外。
- 最后,我们返回损失,并且
hs[len(x)-1]被用作下一个序列的hprev。我们使用缓存来获取反向传播过程中的梯度。
选择使用索引[t][l]来存储在时间步‘t’处第‘l’层的隐藏状态。这是因为模型一次处理一个时间步的输入序列,并且在每个时间步,它更新每一层的隐藏状态。通过使用索引[t][l],我们能够跟踪每一层在每个时间步的隐藏状态,从而方便地执行前向传递所需的计算。
此外,这种索引允许轻松访问最后一个时间步的隐藏状态,该状态作为hs[len(x)-1]返回,因为它是每层序列中最后一个时间步的隐藏状态。这个返回的隐藏状态在训练过程中被用作下一个序列的初始隐藏状态。
让我们进行前向传递。请记住,没有批量维度。
# Initialize RNN
num_layers = 3
hidden_size = 100
seq_length = 8
rnn = RNN(hidden_size=hidden_size, vocab_size=vocab_size, seq_length=seq_length, num_layers=num_layers)
x = [char_to_idx[ch] for ch in data[rnn.pointer:rnn.pointer+seq_length]]
y = [char_to_idx[ch] for ch in data[rnn.pointer+1:rnn.pointer+seq_length+1]]
# initialize hidden state with zeros
hprev = [np.zeros((hidden_size, 1)) for _ in range(num_layers)]
## Call RNN
loss, hprev, cache = rnn(inputs=x, targets=y, hprev=hprev)
print(loss)
>> 33.38852380987117
反向传播
首先,了解 RNN 反向传播的一些直观感受。
基本 ANN 和 RNN 在反向传播中的关键区别在于错误在网络中的传播方式。虽然 ANN 和 RNN 都将错误从输出层传播到输入层,但 RNN 还会通过时间反向传播错误,在每个时间步调整权重和偏置。这使得 RNN 能够处理序列数据,并以隐藏状态的形式维持“记忆”。
BPTT(时间反向传播)算法通过展开 RNN 并为每个时间步创建计算图来工作。这个网络的计算图可以在这里查看。
然后为每个时间步计算梯度,并在整个序列上累积。
def backward(self, targets, cache):
"""RNN Backward Pass"""
# unpack cache
xs, hs, ps = cache['xs'], cache['hs'], cache['ps']
# initialize gradients to zero
dWxh, dWhh, dWhy = [np.zeros_like(w) for w in self.Wxh], [np.zeros_like(w) for w in self.Whh], np.zeros_like(self.Why)
dbh, dby = [np.zeros_like(b) for b in self.bh], np.zeros_like(self.by)
dhnext = [np.zeros_like(h) for h in hs[0]]
for t in reversed(range(len(xs))):
dy = np.copy(ps[t])
# backprop into y. see http://cs231n.github.io/neural-networks-case-study/#grad if confused here
dy[targets[t]] -= 1
dWhy += np.dot(dy, hs[t][-1].T)
dby += dy
for l in reversed(range(self.num_layers)):
dh = np.dot(self.Why.T, dy) + dhnext[l]
dhraw = (1 - hs[t][l] * hs[t][l]) * dh # backprop through tanh nonlinearity
dbh[l] += dhraw
dWxh[l] += np.dot(dhraw, xs[t].T)
dWhh[l] += np.dot(dhraw, hs[t-1][l].T)
dhnext[l] = np.dot(self.Whh[l].T, dhraw)
return {'dWxh':dWxh, 'dWhh':dWhh, 'dWhy':dWhy, 'dbh':dbh, 'dby':dby}
与前向传递相同,让我们分解它。
这个函数的第一步是将权重和偏置的梯度初始化为零,这类似于前馈 ANN 中的情况。这是让我困惑的一点,因此我会进一步详细解释。
通过在每个序列之前将梯度重置为零,确保当前序列计算的梯度不会与先前序列计算的梯度累积或叠加。
这可以防止梯度变得过大,从而导致优化过程发散并对模型性能产生负面影响。此外,它允许对每个序列独立执行权重更新,这可以导致更稳定和一致的优化。
然后,它会反向遍历输入序列,对每个时间步 t 执行以下计算:
注意注释,回传到 y,这个链接将完美解释发生了什么。我也在之前的文章中深入探讨了这一点,你可以在这里查看。
-
计算隐藏状态
hs[t][l]相对于损失的梯度,用dh表示。 -
计算原始隐藏状态的梯度,用
dhraw表示
dh 和 dhraw 的区别是什么? 好问题。
dh和dhraw的区别在于,dh是相对于损失的隐藏状态hs[t][l]的梯度,通过反向传播输出层 softmax 激活的概率ps[t]的梯度计算得出。dhraw是相同的梯度,但它进一步通过非线性 tanh 激活函数反向传播,通过元素级相乘隐藏状态dh的梯度与 tanh 函数的导数(1 - hs[t][l] * hs[t][l])得到。
-
计算隐藏偏置
bh[l]的梯度 -
计算相对于损失的输入-隐藏权重
Wxh[l]的梯度,用dWxh[l]表示。 -
计算相对于损失的隐藏-隐藏权重
Whh[l]的梯度,用dWhh[l]表示。 -
计算下一个隐藏状态
dhnext[l]的梯度。
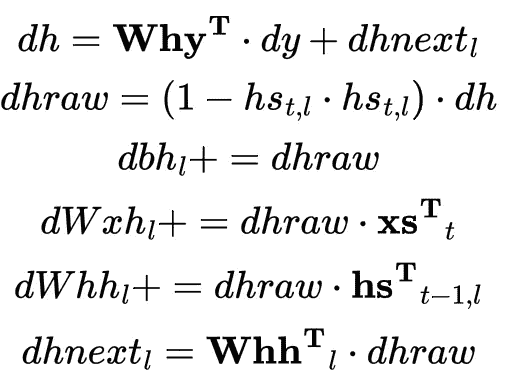
反向传递计算的数学符号。作者提供的图像。
让我们进行反向传递。
# Initialize RNN
num_layers = 3
hidden_size = 100
seq_length = 8
rnn = RNN(hidden_size=hidden_size, vocab_size=vocab_size, seq_length=seq_length, num_layers=num_layers)
x = [char_to_idx[ch] for ch in data[rnn.pointer:rnn.pointer+seq_length]]
y = [char_to_idx[ch] for ch in data[rnn.pointer+1:rnn.pointer+seq_length+1]]
# initialize hidden state with zeros
hprev = [np.zeros((hidden_size, 1)) for _ in range(num_layers)]
## Call RNN
loss, hprev, cache = rnn(inputs=x, targets=y, hprev=hprev)
grads = rnn.backward(targets=y, cache=cache)
最后,我们返回梯度,以便更新参数,这也是我下一个话题——优化的引子。
优化器
如 RNN 类中的‘update’方法所述,我们将使用 Adagrad 进行这个实现。
Adagrad 是一种优化算法,它根据历史梯度信息为神经网络中的每个参数单独调整学习率。
它特别适用于处理稀疏数据,通常用于自然语言处理任务。Adagrad 在每次迭代时调整学习率,确保模型尽可能快速和高效地从数据中学习。
def update(self, grads, lr):
"""Perform Parameter Update w/ Adagrad"""
# unpack grads
dWxh, dWhh, dWhy = grads['dWxh'], grads['dWhh'], grads['dWhy']
dbh, dby = grads['dbh'], grads['dby']
# loop through each layer
for i in range(self.num_layers):
# clip gradients to mitigate exploding gradients
np.clip(dWxh[i], -5, 5, out=dWxh[i])
np.clip(dWhh[i], -5, 5, out=dWhh[i])
np.clip(dbh[i], -5, 5, out=dbh[i])
# perform parameter update with Adagrad
self.mWxh[i] += dWxh[i] * dWxh[i]
self.Wxh[i] -= lr * dWxh[i] / np.sqrt(self.mWxh[i] + 1e-8)
self.mWhh[i] += dWhh[i] * dWhh[i]
self.Whh[i] -= lr * dWhh[i] / np.sqrt(self.mWhh[i] + 1e-8)
self.mbh[i] += dbh[i] * dbh[i]
self.bh[i] -= lr * dbh[i] / np.sqrt(self.mbh[i] + 1e-8)
# clip gradients for Why and by
np.clip(dWhy, -5, 5, out=dWhy)
np.clip(dby, -5, 5, out=dby)
# perform parameter update with Adagrad
self.mWhy += dWhy * dWhy
self.Why -= lr * dWhy / np.sqrt(self.mWhy + 1e-8)
self.mby += dby * dby
self.by -= lr * dby / np.sqrt(self.mby + 1e-8)
这段代码使用 Adagrad 优化算法更新 RNN 的参数。它跟踪参数的梯度平方和(mWxh、mWhh、mbh、mWhy 和 mby),并用这个和的平方根加上一个小常数 1e-8 来除以学习率,以确保数值稳定,从而有效地调整每个参数的学习率。此外,它剪切梯度以防止 梯度爆炸。
Adagrad 为每个参数调整学习率,对不频繁更新的参数执行较大的更新,对频繁更新的参数执行较小的更新。这意味着,对于不频繁更新的参数,学习率会较大,以便模型能对这些参数做出更大的调整。另一方面,对于频繁更新的参数,学习率会较小,从而使模型对这些参数进行小幅调整,以防过拟合。这与使用固定学习率形成对比,后者可能会导致参数校正不足或过度校正。
让我们进行参数更新。
# Initialize RNN
num_layers = 3
hidden_size = 100
seq_length = 8
rnn = RNN(hidden_size=hidden_size, vocab_size=vocab_size, seq_length=seq_length, num_layers=num_layers)
x = [char_to_idx[ch] for ch in data[rnn.pointer:rnn.pointer+seq_length]]
y = [char_to_idx[ch] for ch in data[rnn.pointer+1:rnn.pointer+seq_length+1]]
# initialize hidden state with zeros
hprev = [np.zeros((hidden_size, 1)) for _ in range(num_layers)]
## Call RNN
loss, hprev, cache = rnn(inputs=x, targets=y, hprev=hprev)
grads = rnn.backward(targets=y, cache=cache)
rnn.update(grads=grads, lr=1e-1)
训练
最后一步实际上是训练网络,将输入序列输入网络中,计算错误,优化器更新权重和偏差。
def train(rnn, epochs, data, lr=1e-1, use_drop=False):
for _ in range(epochs):
# prepare inputs (we're sweeping from left to right in steps seq_length long)
if rnn.pointer+seq_length+1 >= len(data) or rnn.iteration == 0:
hprev = [np.zeros((hidden_size, 1)) for _ in range(rnn.num_layers)] # reset RNN memory
rnn.pointer = 0 # go from start of data
x = [char_to_idx[ch] for ch in data[rnn.pointer:rnn.pointer+seq_length]]
y = [char_to_idx[ch] for ch in data[rnn.pointer+1:rnn.pointer+seq_length+1]]
if use_drop:
loss, hprev, cache = rnn(inputs=x, targets=y, hprev=hprev, dropout=True)
else:
loss, hprev, cache = rnn(inputs=x, targets=y, hprev=hprev)
grads = rnn.backward(targets=y, cache=cache)
rnn.update(grads=grads, lr=lr)
# update loss
rnn.loss = rnn.loss * 0.999 + loss * 0.001
## show progress now and then
if rnn.iteration % 1000 == 0:
print('iter {}, loss: {}'.format(rnn.iteration, rnn.loss))
sample_ix = rnn.predict(hprev, x[0], 200)
txt = ''.join(idx_to_char[ix] for ix in sample_ix)
print('Sample')
print ('----\n {} \n----'.format(txt))
rnn.pointer += seq_length # move data pointer
rnn.iteration += 1 # iteration counter
## hyper-params
num_layers = 2
hidden_size = 128
seq_length = 13
# Initialize RNN
rnn = RNN(hidden_size=hidden_size,
vocab_size=vocab_size,
seq_length=seq_length,
num_layers=num_layers)
train(rnn=rnn, epochs=15000, data=data)
这段代码非常简单。我们执行前向和反向传播,并在每个纪元更新模型参数。
我想指出的是——
损失通过当前损失和前一个损失的加权平均来更新。
当前损失乘以 0.001 并加到前一个损失上,前一个损失乘以 0.999。这意味着当前损失对总损失的影响较小,而前面的损失影响较大。这样,总损失波动不会那么大,并且会随着时间更加稳定。
通过使用 EMA(指数移动平均),更容易监控网络的性能,并检测它是否过拟合或欠拟合。

第零次迭代的损失与文本预测。图片由作者提供。
第 14,000 次迭代的损失与文本预测。图片由作者提供。

50,000 个纪元后的损失。
我们的 RNN 训练过程已经成功,我们可以看到损失的减少和生成样本质量的提高。然而,需要注意的是,生成原创莎士比亚文本是一个复杂的任务,而这一实现是一个简单的普通 RNN。因此,仍有进一步改进和尝试不同架构和技术的空间。
结论
总之,本文展示了如何使用 Numpy 实现和训练一个字符级 RNN。多对多架构和在线学习方法使得网络能够适应数据中的新模式,从而改进样本生成。虽然这个网络在生成原创莎士比亚文本方面具有一定能力,但需要注意的是,这只是一个简化版本,还有许多其他架构和技术可以探索,以获得更好的性能。
完整代码和仓库 在这里。
随时与我们联系并提出问题,或对代码进行改进。
感谢阅读!














































 722
722

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








