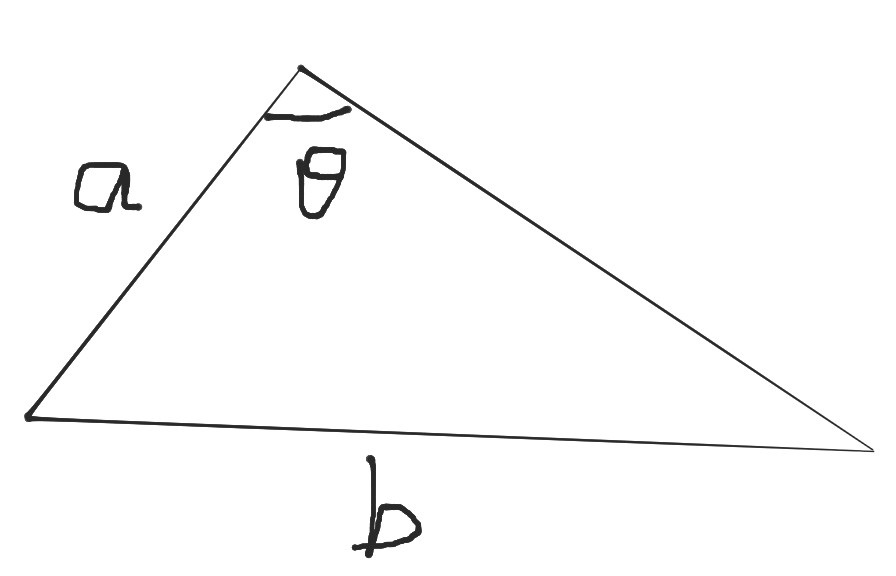
已知三角形中的一个角 θ \theta θ和其对边 b b b以及侧边 a a a,
c 2 = a 2 + b 2 − 2 a 2 s i n 2 θ ± 2 a ( b 2 − a 2 s i n 2 θ ) c o s 2 θ c^2=a^2+b^2-2a^2sin^2\theta\pm 2a\sqrt{(b^2-a^2sin^2\theta)cos^2\theta} c2=a2+b2−2a2sin2θ±2a(b2−a2sin2θ)cos2θ
证明很简单, 用海伦公式和三角形两边一内角的面积公式, 消去公共面积变量即可.
{
S
=
1
2
a
c
⋅
s
i
n
θ
S
=
p
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
其
中
p
=
(
a
+
b
+
c
)
/
2
\begin{cases} S=\frac{1}{2}ac\cdot sin \theta \\ \\ S=\sqrt{p(p-a)(p-b)(p-c)} ~~~~~~~~~~~~~~~ 其中p=(a+b+c)/2 \end{cases}
⎩⎪⎨⎪⎧S=21ac⋅sinθS=p(p−a)(p−b)(p−c) 其中p=(a+b+c)/2
要说明的是, 当
θ
<
π
/
2
\theta<\pi/2
θ<π/2且
b
<
a
b<a
b<a时,
c
c
c有两个解, 其他条件下只有一个解,
±
\pm
±只需要取
−
-
−即可.
扫一扫
6522
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
