（ICCV-2021）通过有效的全局-局部特征表示和局部时间聚合进行步态识别（二）

3. Proposed Method

---

\quad \quad 在本节中，首先概述了所提出方法的框架。然后描述了所提出方法的关键组件，包括局部时间聚合(LTA)、全局和局部特征提取器 (GLFE) 和广义均值(GeM)池化层。最后，介绍了训练和测试的细节。

---

3.1. Overview

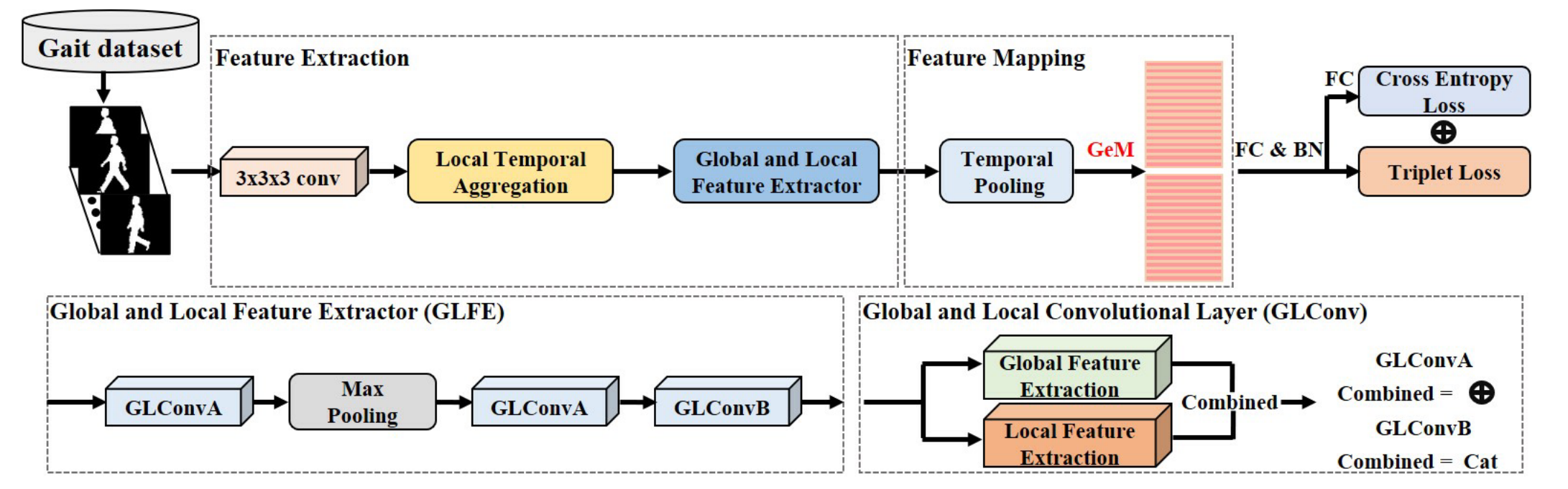
\quad \quad 所提出方法的概述如图1所示，其目的是为步态识别提取更全面的特征表示，包括三个关键组成部分。首先，使用卷积从原始输入序列中提取浅层特征。接下来，局部时间聚合（LTA）操作被设计用来聚合时间信息，并保留更多的空间信息进行权衡。之后，用全局和局部特征提取器（GLFE）来提取融合全局和局部信息的组合特征。然后，利用时间池化和 GeM 池化层来实现特征映射。最后，选择三元组损失和交叉熵损失来训练所提出的模型。

---

3.2. Local Temporal Aggregation

\quad \quad 以前的工作使用特定模式“CL-SP-CL-SP-CL”来提取特征，其中 CL 表示卷积层，SP 表示空间池化层。然而，空间信息可能会因 SP 下采样操作而丢失。考虑到步态序列中的时间信息是周期性的，提出了LTA操作来代替第一个空间池化层，它可以整合局部剪辑的时间信息并保留更多的空间信息。

\quad \quad 假设$X_{in}\in {\mathbb{R}}^{C_1\times T_1\times H_1\times W_1}$是局部时间聚合的输入，其$C_1$是通道数，$T_1$是步态序列的长度,$(H_1,W_1)$是每帧的图像大小。该过程可以表述如下:
$$X_{LTA}=f_{a\times a\times a}^{b\times 1\times 1}\left(X_{in}\right)$$
其中$f_{a\times a\times a}^{b\times 1\times 1}\left(\cdot \right)$表示核大小为$a$和时间步长为$b$的3D卷积操作。$X_{LTA}\in {\mathbb{R}}^{C_2\times T_2\times H_1\times W_1}$是LTA操作的输出。

---

3.3. Global and Local Feature Extractor

\quad \quad 除了全局步态特征，最近的一些研究人员提出了利用局部步态信息的不同步态识别框架，如图2(a)(b)所示。例如，Zhang等人提出 ACL 框架通过使用多个单独的 2D CNN 来提取局部步态特征。Fan等人开发了一个焦点卷积层来提取局部特征，然后将它们组合起来。虽然它比全局步态特征包含更详细的信息，但局部步态特征并不关注局部区域之间的关系。因此，提出了一种新的GLFE模块来提取特征，该模块可以利用全局和局部信息。GLFE 模块由 GLConv 层实现，GLConv层包含全局和局部特征提取器。全局特征提取器可以提取整个步态信息，而局部特征提取器用于从局部特征图中提取更多细节。由于组合不同，GLConv有两种不同的结构，例如GLConvA和GLConvB。如图1所示，GLFE模块包括四层，“GLConvA-SP-GLConvA-GLConvB”。

\quad \quad GLConv 层如图 2© 所示。假设它的输入是$X_{\text{global }}\in {\mathbb{R}}^{c_1\times t\times h\times w}$，其中$c_1$是通道数,$t$是特征图的长度，$(h,w)$是每帧的图像大小。首先将全局特征图划分为 n 部分作为局部特征图$X_{local}=\left\{X_{\text{local }}^i\mid i=1,\dots ,n\right\}$,其中n是划分区域数。$X_{\text{local }}^i\in {\mathbb{R}}^{c_1\times t\times \frac{h}{n}\times w}$对应第 i 个局部步态部分。然后，使用3D卷积分别提取全局和局部步态特征。注意，所有局部特征图共享相同的卷积权重。有两种方法可以组合全局和局部特征图，即通过逐元素加法(GLconvA) 或通过串联 (GLconvB)。GLconvA 和 GLconvB 层可以表示为:
$$Y_{GL\text{ ConvA }}=Y_{\text{global }}+Y_{\text{local }}\in {\mathbb{R}}^{c_2\times t\times h\times w}$$
$$Y_{GLC\text{ onvB }}=\text{ cat }\left\{\begin{array}{c}{Y}_{\text{global }}\\ Y_{\text{local }}\end{array}\right\}\in {\mathbb{R}}^{c_2\times t\times 2h\times w}$$
其中cat表示串联操作。$Y_{global}$和$Y_{local}$可以表示为
$$Y_{\text{global }}=f_{3\times 3\times 3}\left(X_{\text{global }}\right)\in {\mathbb{R}}^{c_2\times t\times h\times w}$$
$$Y_{\text{local }}=cat\left\{\begin{array}{c}{f}_{3\times 3\times 3}^{\prime }\left(Y_{\text{local }}^1\right)\\ f_{3\times 3\times 3}^{\prime }\left(Y_{\text{local }}^2\right)\\ \dots \\ f_{3\times 3\times 3}^{\prime }\left(Y_{\text{local }}^n\right)\end{array}\right\}\in {\mathbb{R}}^{c_2\times t\times h\times w}$$
其中$f_{3\times 3\times 3}(\cdot )$和$f_{3\times 3\times 3}^{\prime }(\cdot )$表示卷积核大小为3的3D卷积。

\quad \quad 基于以上两种形式的GLGonv层，可以构建GLFE模块，在LTA操作后提取步态特征。在实验中，GLConvA被用来实现前几个GLGonv块，GLConvB被用来实现GLFE模块中的最后一个块。

图 2. 不同步态特征提取器的架构。$\oplus$代表逐元素相加，Concat”是指将不同部分的特征图水平串联起来。“2DCNN”表示二维卷积神经网络，“conv2d”表示2D卷积操作，“conv3d”表示3D卷积操作。

---

3.4. Feature Mapping

\quad \quad 由于输入步态序列的长度可能不同，引入了时间池化来聚合整个序列的时间信息。假设GLFE模块的输出是$X_{GLFE}\in {\mathbb{R}}^{C_3\times T_2\times H_2\times W_2}$，其中C3是输入通道的数量，T2是特征图的长度，$(H_2,W_2)$是每帧中特征的空间大小。由于GLFE模块中的空间池化层，空间大小变为$(H_2,W_2)$，而特征图的长度保持不变。时间池化$TP(\cdot )$可以通过以下方式实现
$$Y_{TP}=F_{\text{Max }}^{T_2\times 1\times 1}\left(X_{GLFE}\right)$$
其中$F_{\mathrm{Max}}^{T_2\times 1\times 1}(\cdot )$表示最大池化层。时间池化的输出是$Y_{TP}\in {\mathbb{R}}^{C_3\times 1\times H_2\times W_2}$

\quad \quad 为了提高特征表示能力，研究者开发了加权求和的空间特征映射操作。在时间池化之后，步态特征图被分成条带，并使用两个统计函数 max 和 average 来聚合每个条带的信息。空间特征映射可以表示为
$$Y_{MA}=\alpha F_{Max}^{1\times 1\times W_2}\left(Y_{TP}\right)+\beta F_{Avg}^{1\times 1\times W_2}\left(Y_{TP}\right)$$
其中$Y_{MA}\in {\mathbb{R}}^{C_3\times 1\times H_2\times 1}$是空间特征映射的输出。然而，加权和策略不灵活，因为权衡参数是手动预定义的。

\quad \quad 因此，引入了广义平均池化（GeM）来自适应地整合空间信息。GeM 池化层$GeM(\cdot )$可以表示为
$$Y_{GeM}={\left(F_{Avg}^{1\times 1\times W_2}\left({\left(Y_{TP}\right)}^p\right)\right)}^{\frac{1}{p}}$$
其中$Y_{GeM}\in {\mathbb{R}}^{C_3\times 1\times H_2\times 1}$是 GeM 操作的输出。$p$是可以通过网络训练学习的参数。具体来说，如果$p=1$，则$Y_{GeM}$等于$Av{g}^{1\times 1\times W_2}\left(Y_{TP}\right)$，如果$p\to \infty$，则$Y_{GeM}$等于${\mathrm{Max}}^{1\times 1\times W_2}\left(Y_{TP}\right)$。然后，使用多个独立的全连接层进一步聚合来自$Y_{GeM}$通道的信息。特征映射可以定义为
$$Y_{\text{out }}=F_{\text{sfc }}\left(Y_{\text{GeM }}\right)\in {\mathbb{R}}^{C_4\times 1\times H_2\times 1}$$
$Y_{\text{out }}$是具有$H_2$个水平特征的特征映射的输出，每个特征有$C_4$个通道。$F_{sfc}(\cdot )$表示多个独立的全连接层。

---

3.5. Loss Function

\quad \quad 为了有效地训练所提出的步态识别模型，同时使用了三元组损失和交叉熵损失。

\quad \quad 三元组损失可以提高类间距离并减少类内距离，这有助于交叉熵损失来识别人类ID。在训练阶段，$Y_{out}$ 的每个水平特征都被输入到组合损失函数中，独立计算损失。组合损失函数$L_{\text{combined }}$可以定义为
$$L_{\text{combined }}=L_{\text{tri }}+L_{\text{cse }}$$
其中$L_{tri}$和$L_{cse}$分别表示三元组损失和交叉熵损失.$L_{tri}$可以被定义为
$$L_{tri}=[D(F(i),F(k))-D(F(i),F(j))+m{]}_{+}$$
其中$i$和$j$是来自同一类A的样本，而$k$代表来自B类的样本。$F(\cdot )$表示所提出方法的特征提取和映射操作。$D\left(d_1,d_2\right)$是$d_1$和$d_2$之间的欧式距离。$m$是三元组损失的margin。操作$[\gamma {]}_{+}$等于$\max (\gamma ,0)$。

---

3.6. Training Details and Test

\quad \quad Training Stage. 在训练阶段，首先将输入的步态序列输入到所提出的网络中生成步态特征表示$Y_{out}$。然后，使用组合损失函数计算损失，并采用Batch ALL (BA)作为采样策略.具体来说，每批包含$P$个受试者ID，从每个受试者ID中选择$K$个样本。相应地，批大小为$P\times K$。在训练阶段，考虑到内存限制，将输入序列的长度设置为$T$。

\quad \quad Test Stage. 在测试阶段，将整个步态序列放入提出的网络中以获得步态特征表示$Y_{out}$。然后，$Y_{\text{out }}\in {\mathbb{R}}^{C_4\times 1\times H_2\times 1}$可以展平为一个维度为$C_4\times H_2$的特征向量，然后作为样本。为了计算 Rank-1 准确率，测试数据集分为两组，即注册集（gallery set）和验证集（probe set）。注册集被视为要检索的标准视角，而probe的特征向量被用来匹配gallery视角中的特征向量。多种度量策略，如欧氏距离和余弦距离，可用于计算注册集和验证集之间的相似度。具体而言，选择欧氏族距离作为度量策略。