2023优化算法之红尾鹰算法（RTH），原理公式详解，附matlab代码

红尾鹰算法（Red‑tailed hawk algorithm，RTH）是一种新型群智能优化算法，该算法模拟了红尾鹰的狩猎行为，具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2023年发表在知名SCI期刊Scientific Reports上，目前在谷歌学术上被引4次。

红尾鹰(Buteo jamaicensis)是一种猛禽，在北美大部分地区繁殖。红尾鹰生活在不同的环境和海拔，如沙漠、草原、森林、农田和城市。作为一种食肉动物，它们遇到的每一种小动物都可能被视为猎物。

红尾鹰的狩猎过程分为三个阶段。在高空翱翔阶段，红尾鹰探索搜索空间，确定具有猎物位置的区域；在低空翱翔阶段，红尾在猎物周围的选定区域内移动，以选择狩猎的最佳位置。然后，红尾鹰在急转和俯冲阶段摆动并击中目标。

算法原理

（1）高空翱翔

红尾鹰以温和的二面体飞行，尽可能少地拍动翅膀以节省能量，与其他鹰不同，红尾鹰可以飞行很长的距离，这就是红尾鹰的特点。

在此阶段中，红尾鹰会飞到很远的天空，寻找食物供应方面的最佳位置，此时，它会尽可能少拍动翅膀以节省能量探索所选区域，下式为该阶段的数学模型：  其中，X(t)表示迭代t时红尾鹰的位置，Xbest为获得的最佳位置，Xmean为位置的均值，Levy为Levy飞行分布函数，其数学表达式如下： 

其中s为常数(0.01)，dim为问题维数，β为常数(1.5)，u和υ为随机数[0 ~ 1]。TF(t)为根据下式可计算的过渡因子函数：  

其中Tmax表示最大迭代次数。

（2）低空盘旋

红尾鹰在上一阶段中选择目标位置后，它会绕着猎物进行盘旋低飞，这种移动使它能够探测到击中目标的最佳位置和时间，并给予猎物致命一击，其数学模型如下： 

其中，X(t)表示迭代t时红尾鹰的位置，Xbest为获得的最佳位置，x、y表示方向坐标，可以计算如下：

其中，R0为半径的初值[0.5-3]，A为角度增益[5-15]，rand为随机增益[0-1]，r为控制增益[1,2]。这些参数帮助鹰绕着猎物盘旋飞行，同时提高红尾鹰捕猎的成功率。

（3）俯冲捕食阶段

在这一阶段中，红尾鹰在前一步选择了最佳的位置和时刻后突然弯腰并从低空飞行阶段的最佳位置攻击猎物，该阶段十分迅速，其数学表达式如下：  该阶段的每个步长可以如下计算

式中，α为加速度因子，G为重力因子，可分别定义为： 

其中，α表示鹰的加速度，随着t的增加而增加，以提高收敛速度；G重力因子，当鹰离猎物较近时，重力效应减小，以减少捕食多样性。

由于基于Levy函数的高飙升阶段，红尾鹰避免了在局部极小值上尝试，低突飞提高了开发阶段的收敛速度，而俯仰和俯冲阶段则提高了RTH算法的精度。

---

结果展示

在CEC2005函数集测试，结果如下：

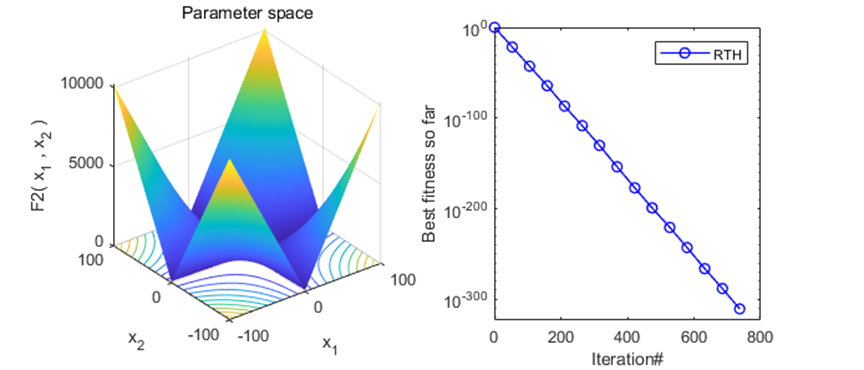
 MATLAB核心代码

function [Cost, Pos, Convergence_curve]=RTH(N,Tmax,low,high,dim,fobj)
Xbestcost = inf; Xbestpos = rand(N,dim);
for i=1:N
    Xpos(i,:) = low+(high-low).*rand(1,dim);
    Xcost(i)=fobj(Xpos(i,:));
    if Xcost(i) < Xbestcost
        Xbestpos = Xpos(i,:);
        Xbestcost = Xcost(i);
    end
end
A=15;
R0=0.5;
r = 1.5;
for t=1:Tmax
    %%               1- High Soaring
    Xmean=mean(Xpos);
    TF = 1+sin(2.5-t/Tmax); % TF
    for i=1:N
        Xnewpos=Xbestpos+(Xmean-Xpos(i,:)).*Levy(dim)*TF;
        Xnewpos = max(Xnewpos, low);
        Xnewpos = min(Xnewpos, high);
        Xnewcost=fobj(Xnewpos);
        if Xnewcost<Xcost(i)
           Xpos(i,:) = Xnewpos;
           Xcost(i)= Xnewcost;
             if Xcost(i) < Xbestcost
              Xbestpos= Xpos(i,:);
             Xbestcost=Xcost(i); 
             end
        end
    end
    %%                2- Low Soaring
    Xmean=mean(Xpos);
    for i=1:N-1
        aa=randperm(N);
        Xpos=Xpos(aa,:);
        Xcost=Xcost(aa);
        [x y]=polr(A,R0,N,t,Tmax,r);
        StepSize=Xpos(i,:)-Xmean;
        Xnewpos = Xbestpos +(y(i)+x(i))*StepSize;
        Xnewpos = max(Xnewpos, low);
        Xnewpos = min(Xnewpos, high);
        Xnewcost=fobj(Xnewpos);
        if Xnewcost<Xcost(i)
           Xpos(i,:) = Xnewpos;
           Xcost(i)= Xnewcost;
           if Xcost(i) < Xbestcost
                     Xbestpos= Xpos(i,:);
                    Xbestcost=Xcost(i);
           end
        end
    end
    %%                3- Stopping & Swooping
    Xmean=mean(Xpos);
    TF = 1+0.5*sin(2.5-t/Tmax); 
    for i=1:N
        b=randperm(N);
        Xpos=Xpos(b,:);
        Xcost=Xcost(b);
        [x y]=polr(A,R0,N,t,Tmax,r);
        alpha=(sin(2.5-t/Tmax).^2);
        G=2*(1-(t/Tmax));
        StepSize1 = 1.*Xpos(i,:) - TF*Xmean;
        StepSize2= G.*Xpos(i,:)-TF*Xbestpos;
        Xnewpos = alpha*Xbestpos+x(i)*StepSize1+y(i)*StepSize2;
        Xnewpos = max(Xnewpos, low);
        Xnewpos = min(Xnewpos, high);
        Xnewcost=fobj(Xnewpos);
        if Xnewcost<Xcost(i)
           Xpos(i,:) = Xnewpos;
           Xcost(i)= Xnewcost;
           if Xcost(i) < Xbestcost
                     Xbestpos= Xpos(i,:);
                    Xbestcost=Xcost(i); 
           end
        end
    end
    Convergence_curve(t)=Xbestcost;
    Cost = Xbestcost;
    Pos = Xbestpos;
end
 function [xR yR]=polr(A,R0,N,t,MaxIt,r)
%// Set parameters
th = (1+t/MaxIt)*A*pi*rand(N,1);
R  =(r-t/MaxIt)*R0*rand(N,1); 
xR = R.*sin(th);
yR = R.*cos(th);
 xR=xR/max(abs(xR));
 yR=yR/max(abs(yR));
 function o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;

参考文献

[1] Ferahtia S, Houari A, Rezk H, et al. Red-tailed hawk algorithm for numerical optimization and real-world problems[J]. Scientific Reports, 2023, 13(1): 12950.

完整代码获取方式：后台回复关键字：

TGDM100