2024年JCR1区新算法：PID搜索算法，原理详解，MATLAB代码免费获取

PID搜索算法（PID-based search algorithm, PSA）是一种全新的元启发式优化算法，增量式PID控制使当前时刻的控制量与前一刻的控制量之差，这个差就是新的控制量，这是一种递归算法。PSA是数学建模和实现，以实现在广泛的搜索空间的优化。通过与近年来提出的7种元启发式算法的比较，验证了该算法的优化性能，该算法具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2024年发表在计算机领域一区期刊The Journal of Supercomputing上，在多类实际工程问题上也得到了很好的验证。

用户设定目标值后，增量式PID控制器给致动器输出值，致动器根据输出值对被控对象进行调节。被控对象调整后的真实值由传感器获取，并再次传递给增量PID控制器。该算法基于增量PID控制器，通过不断调整系统偏差，使整个种群收敛到最优状态。增量式PID控制是一种比例积分导数控制，其调节过程如下图所示。

1、算法原理

（1）种群初始化

优化问题由一组决策变量、约束和目标函数组成。可以假设该组决策变量的个数为d，变量的上界为u，下界为l。PSA的控制参数包括最大迭代次数T和种群大小n，则初始种群可表示为

式中xij表示第I个个体的第j维;Uj和lj分别是第j个变量(维)的上界和下界;R1是0到1之间的随机数。

假设目标函数为f，则第i个个体的目标函数值fi可由下式计算。

（2）增量PID计算系统偏差

对于最小化问题，迭代次数t处的最佳个体x*(t)是种群历史最小值所对应的个体。对于若干次迭代，总体的偏差周(t)为

为了便于计算和迭代更新，当迭代次数为t时，将前一次迭代的总体偏差分别表示为ek−1(t)，将前两次迭代的总体偏差分别表示为ek−2(t)。那么当t = 1时，可以令ek−2(t) = ek−1(t) = ek(t)。当t > 1时，ek−2(t) = ek−1(t−1)。在PID算法中，当t > 1时，ek−1应等于前一刻系统中用户设置值与真实值的偏差。

在PSA中，用户集的值是最优值，但每次迭代后的最优值并不总是不变的;因此，在提出的PSA中，ek−1(t)不能简单地等于ek(t−1)。如下图所示，ek - 1(t)应该等于x*(t) - x(t - 1)，但这也意味着要存储x(t - 1)。

为了尽可能降低算法的空间复杂度，最好将最终的ek - 1(t)写成ek(t - 1)+x*(t) - x*(t - 1)而不是x*(t) - x(t - 1)。因此，ek−1(t)可以表示为

（3）PID调节作用

在现实问题中，比例、积分和微分因子会根据不同的情况和问题进行调整。则当迭代次数为t时，PID调节输出值Δu(t)为

式中r2、r3、r4为n行1列0 ~ 1的随机数向量;Kp、Ki、Kd分别为比例、积分、微分的调整系数，本文分别设为1、0.5、1.2。

在传统的PID算法中，输出调节值为0表示实值在某一点已经达到用户的设定值。然而，随着时间的增加，如果不调整被控对象，真实值将很快不等于设定值。因此，为了防止这种现象，通常在原来的调节值上增加一个常数。所有的解都非常接近最优解，特别是在早期迭代中，这对PSA来说是不利的，这种现象可能导致算法陷入局部最优。因此，在原来的Δu(t)上，本文还增加了一个称为零输出的条件因子，以防止算法陷入局部最优。零输出定义如下式所示：

式中r5为n行d列0 ~ 1随机数的向量;λ为调节系数，由下式计算得到：

λ随t的变化如下图所示。可以看出，λ随着t的增加而缓慢减小，这有助于算法的充分探索。在后期，λ迅速减小，有助于算法从探索转向利用。

上式中的L是一个L´every飞行函数，定义如下式所示：

式中，u和v分别为符合标准正态分布的n行、d列随机数矩阵;β是一个设定为1.5的因子。

所有个体的更新都与Δu(t)和o(t)有关。人口更新公式定义为

式中η为n行1列矩阵，表示为η = r6cos(t/ t)

其中r6是由n行1列0到1个随机数组成的矩阵。PSA的流程图分别如下图所示。

2、结果展示

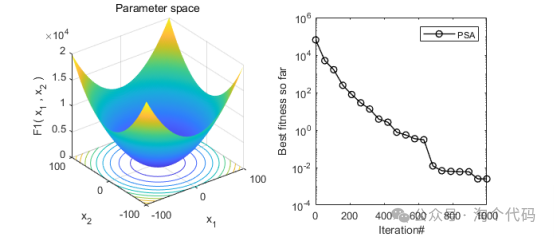
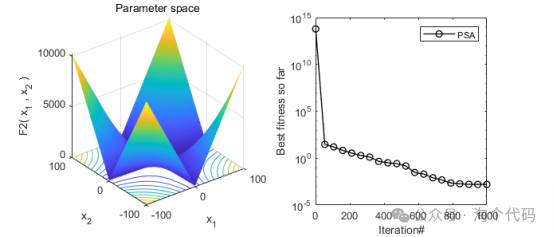
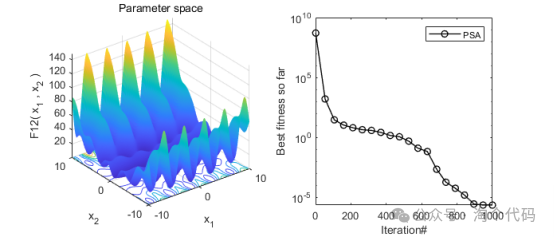
3、MATLAB核心代码

function [TargetX,TargetF,ConvergenceCurve] = PSA (fun,nvars,lb,ub,N,T)
%% Initialization
ConvergenceCurve = zeros(1,T);
t = 1;
Kp = 1;
Ki = 0.5;
Kd = 1.2;
LogT = log(T);
% Create the population
[x, lb, ub]=Initialization(N,nvars,ub,lb);
lbExtended = repmat (lb,[N,1]);
ubExtended = repmat (ub,[N,1]);
% Create the fitness vector
f = zeros(N,1);
for i = 1:N
    f(i,:) = fun (x(i,:));
end
%% main loop
while t<=T
    % Step 1: Guide selection mechanism
    if t == 1
        [TargetF, index]=min(f);
        TargetX = x(index,:);
        newTargetX = TargetX;
        newTargetF = TargetF;
    else
        for i = 1:N
            f(i,:) = fun (x(i,:));
        end
        if min(f)<TargetF
            [newTargetF, index]=min(f);
            newTargetX = x(index,:);
        end
    end
    ConvergenceCurve(t) = newTargetF;
    % Step 2: Search operations
    if t == 1
        Ek = TargetX - x;
        Ek_1 = Ek;
        Ek_2 = Ek;
    else
        Ek_2 = Ek_1;
        Ek_1 = Ek + newTargetX - TargetX;
        Ek = newTargetX - x;
        TargetX = newTargetX;
        TargetF = newTargetF;
    end
    a = (log(T-t+2)/LogT)^2;
    out0 = (cos(1-t/T) + a*rand(N,nvars).*PSA_levyFlight(N,nvars)).*Ek;
    pid = rand(N,1)*Kp.*(Ek-Ek_1) + rand(N,1)*Ki.*Ek + rand(N,1)*Kd.*(Ek - 2*Ek_1 + Ek_2);
    % Step 3: Update mechanism
    r = rand(N,1)*cos(t/T);
    x = x + r.*pid + (1-r).*out0;
    lbViolated = x < lbExtended;
    ubViolated = x > ubExtended;
    x (lbViolated) = lbExtended (lbViolated);
    x (ubViolated) = ubExtended (ubViolated);
    % Next generation until termination criterion
    t = t + 1;
end
end
function o=PSA_levyFlight(n,d)
beta=1.5;
sigma=(gamma(1+beta).*sin(pi*beta/2)./(gamma((1+beta)/2).*beta.*2.^((beta-1)/2))).^(1/beta);
u=randn(n,d)*sigma;
v=randn(n,d);
step=u./abs(v).^(1/beta);
o=step;
end

参考文献

[1]Gao Y. PID-based search algorithm: A novel metaheuristic algorithm based on PID algorithm[J]. Expert Systems With Applications, 2023, 232: 120886.

完整代码获取方式：后台回复关键字：

TGDM877