当我们手中握有大量的数据时,对于二维的数据,我们会对他们进行直线拟合、对数拟合,圆曲线的拟合等等。这些拟合的方法都是运用的了非常古老而又非常有效的方法,即最小二乘法。
今天给大家介绍一种三维球面数据的拟合方法,该方法也是运用的最小二乘的方法。旨在使拟合的半径在均方意义下误差达到最小。
公式推导
设拟合后的球面的球心为(x_0,y_0,z_0)及半径r。
对于每一点拟合后估计的值与实际值的差值为:
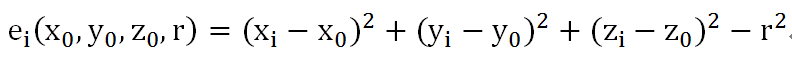
则误差的平方和为:
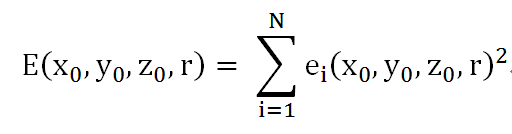
注意E是x_0,y_0,z_0,r的函数。因此令E分别对x_0,y_0,z_0,r的偏导数等于0,即可求出x_0,y_0,z_0,r,有:
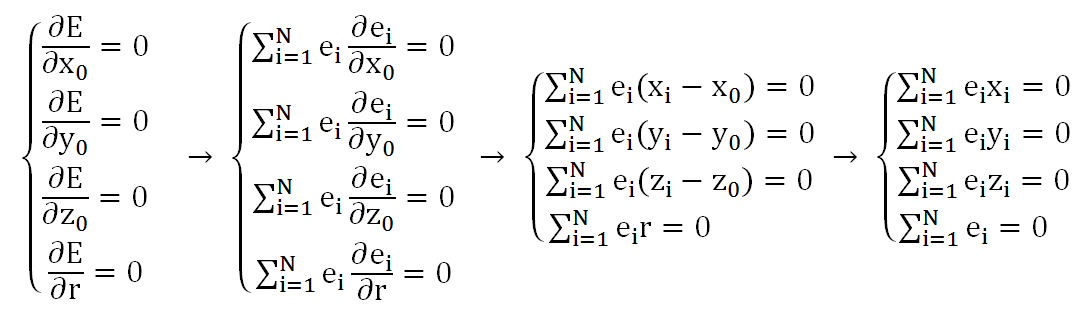
令:
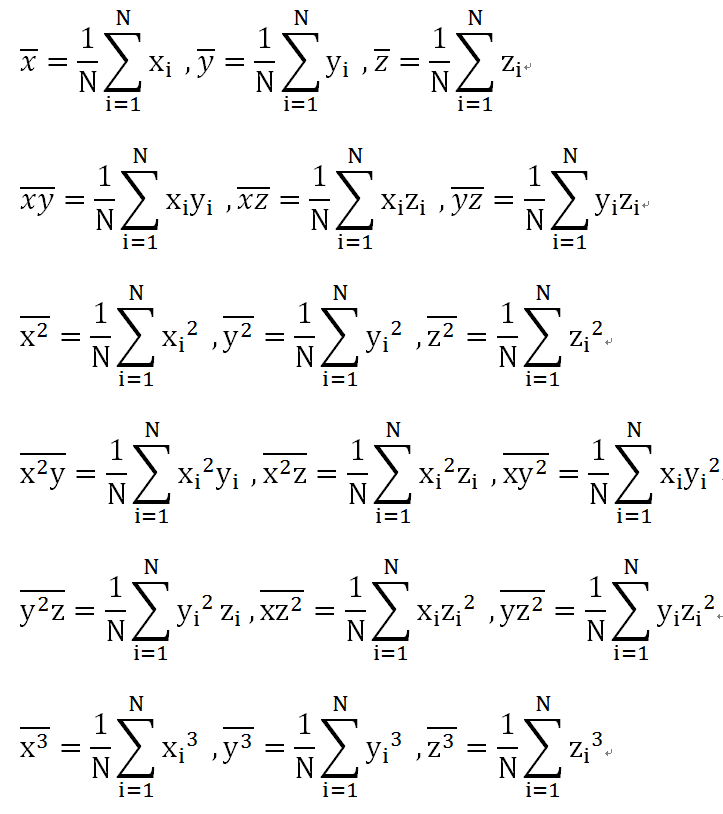
则有:
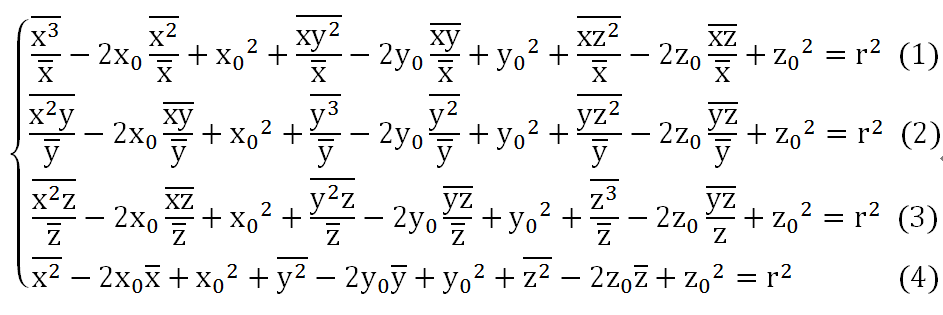
由(1)-(4)得
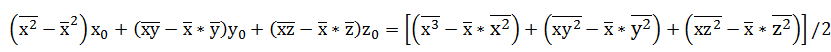
由(2)-(4)得
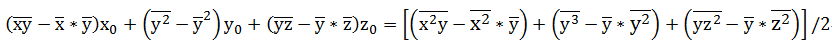
由(3)-(4)得
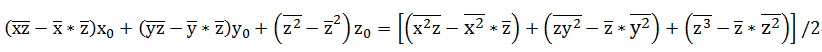
写成矩阵的形式:
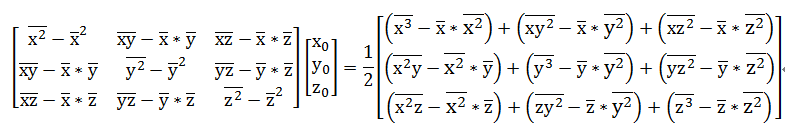
求解该矩阵得到x_0,y_0,z_0值,然后带入(4)式中得到r的值。
Matlab仿真
首先生成若干个球面数据,然后加入一定能量的噪声。最后利用上述的公式计算拟合后的球心坐标和球面半径,下面给出的是matlab仿真代码:
%最小二乘的方法进行拟合
clear all;
close all
clc;
R = 2; %球面半径
x0 = 100; %球心x坐标
y0 = 1; %球心y坐标
z0 = 76; %球心z坐标
%********************************生成随机球面数据************************************
alfa = 0:pi/50:pi;
sita = 0:pi/50:2*pi;
num_alfa = length(alfa);
num_sita = length(sita);
x = zeros(num_alfa,num_sita);
y = zeros(num_alfa,num_sita);
z = zeros(num_alfa,num_sita);
for i = 1:num_alfa
for j = 1:num_sita
x(i,j) = x0+R*sin(alfa(i))*cos(sita(j));
y(i,j) = y0+R*sin(alfa(i))*sin(sita(j));
z(i,j) = z0+R*cos(alfa(i));
end
end
x = reshape(x,num_alfa*num_sita,1);
y = reshape(y,num_alfa*num_sita,1);
z = reshape(z,num_alfa*num_sita,1);
figure;
plot3(x,y,z,'*');
title('生成的没有噪声的球面数据');
%加入均值为0的高斯分布噪声
amp = 0.1;
x = x + amp*rand(num_alfa*num_sita,1);
y = y + amp*rand(num_alfa*num_sita,1);
z = z + amp*rand(num_alfa*num_sita,1);
figure;
plot3(x,y,z,'*');
title('加入噪声的球面数据');
%*******************************************************************************************
%球面拟合算法
num_points = length(x);
x_avr = sum(x)/num_points;
y_avr = sum(y)/num_points;
z_avr = sum(z)/num_points;
xx_avr = sum(x.*x)/num_points;
yy_avr = sum(y.*y)/num_points;
zz_avr = sum(z.*z)/num_points;
xy_avr = sum(x.*y)/num_points;
xz_avr = sum(x.*z)/num_points;
yz_avr = sum(y.*z)/num_points;
xxx_avr = sum(x.*x.*x)/num_points;
xxy_avr = sum(x.*x.*y)/num_points;
xxz_avr = sum(x.*x.*z)/num_points;
xyy_avr = sum(x.*y.*y)/num_points;
xzz_avr = sum(x.*z.*z)/num_points;
yyy_avr = sum(y.*y.*y)/num_points;
yyz_avr = sum(y.*y.*z)/num_points;
yzz_avr = sum(y.*z.*z)/num_points;
zzz_avr = sum(z.*z.*z)/num_points;
%计算求解线性方程的系数矩阵
A = [xx_avr - x_avr*x_avr,xy_avr - x_avr*y_avr,xz_avr - x_avr*z_avr;
xy_avr - x_avr*y_avr,yy_avr - y_avr*y_avr,yz_avr - y_avr*z_avr;
xz_avr - x_avr*z_avr,yz_avr - y_avr*z_avr,zz_avr - z_avr*z_avr];
b = [xxx_avr - x_avr*xx_avr + xyy_avr - x_avr*yy_avr + xzz_avr - x_avr*zz_avr;
xxy_avr - y_avr*xx_avr + yyy_avr - y_avr*yy_avr + yzz_avr - y_avr*zz_avr;
xxz_avr - z_avr*xx_avr + yyz_avr - z_avr*yy_avr + zzz_avr - z_avr*zz_avr];
b = b/2;
resoult = inv(A)*b;
x00 = resoult(1); %拟合出的x坐标
y00 = resoult(2); %拟合出的y坐标
z00 = resoult(3); %拟合出的z坐标
r = sqrt(xx_avr-2*x00*x_avr+x00*x00 + yy_avr-2*y00*y_avr+y00*y00 + zz_avr-2*z00*z_avr+z00*z00); %拟合出的球半径r
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
运行的结果如下:
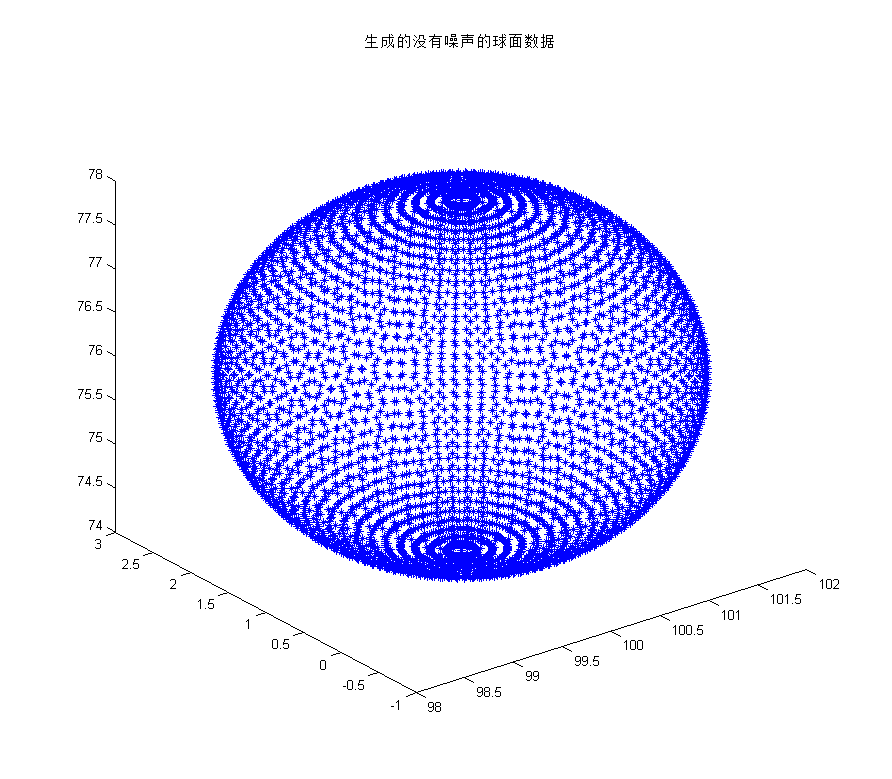
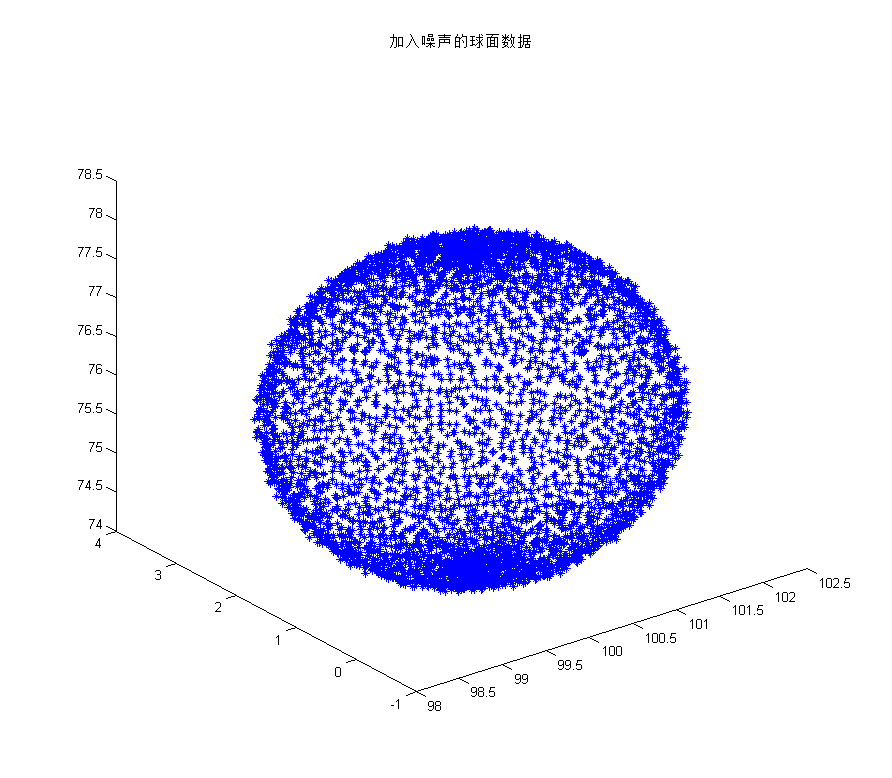
拟合后的x00=100.0502, y00=1.0491, z00=76.0512, r=2.0009与真实的x0=100, y0=1, z0=76, R=2非常的接近。
当然如果得到的球面数据不是在整个球面均匀分布的也可以得到很不错的拟合结果,当得到的数据如下图所示:
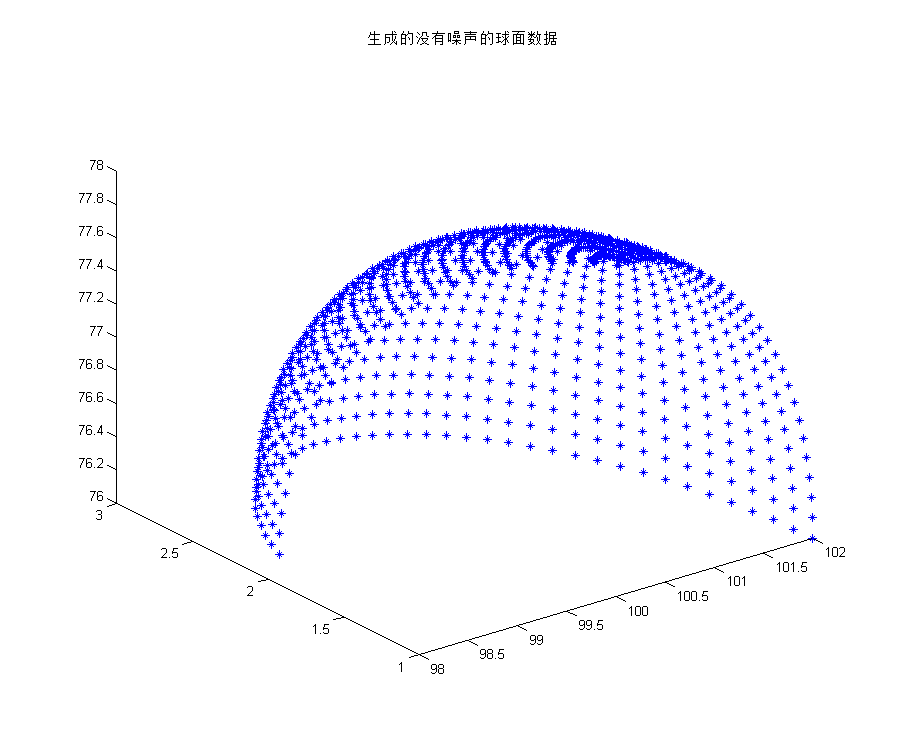
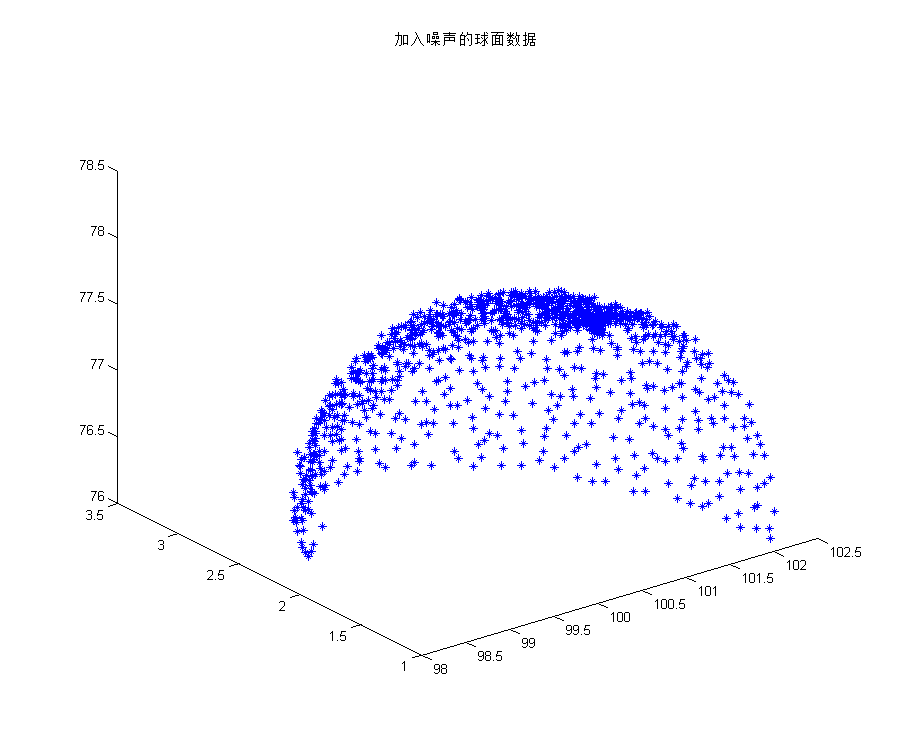
拟合后的x00=100.0510, y00=1.0537, z00=76.0540, r= 1.9952与真实值依然很接近。
原文地址
http://blog.csdn.net/hj199404182515/article/details/53462512
但是个人感觉他的求导推导有问题
欢迎大家一起来讨论一下:

红色标记部分
欢迎高手给以解释,非常感谢
扫码关注我们:跟着数理化走天下
获得更多的信息哦,一起交流,一起成长哦:微信号:跟着数理化走天下,纯属个人的交流,无盈利目的

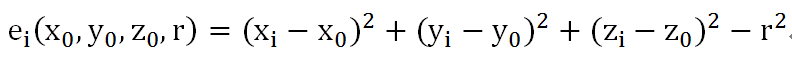
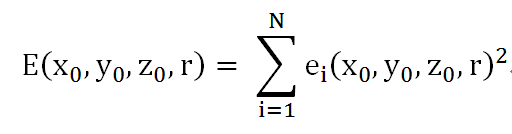
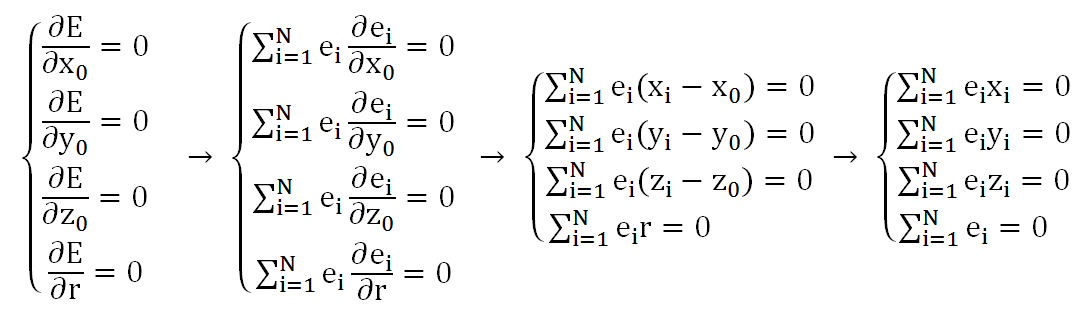
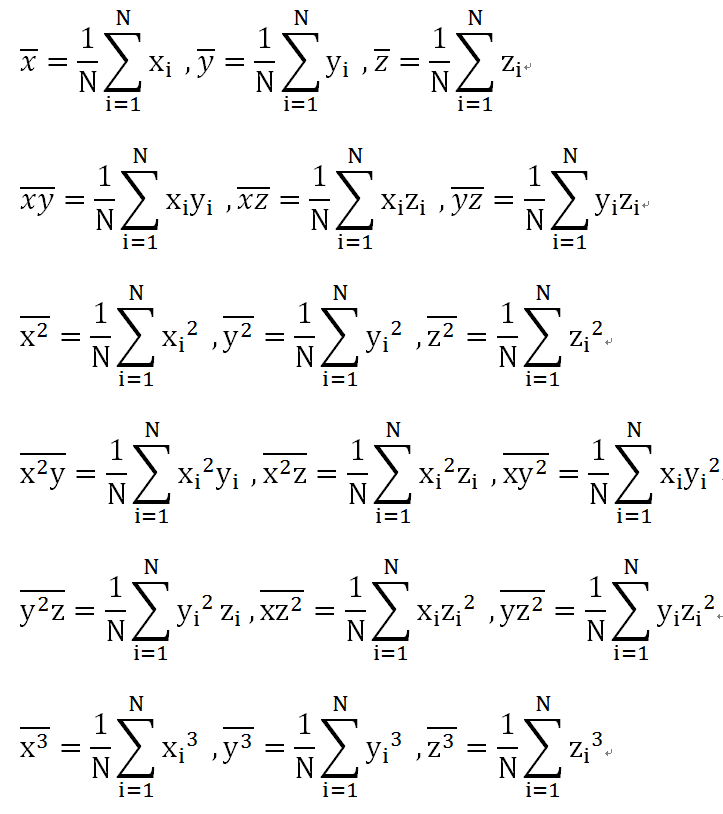
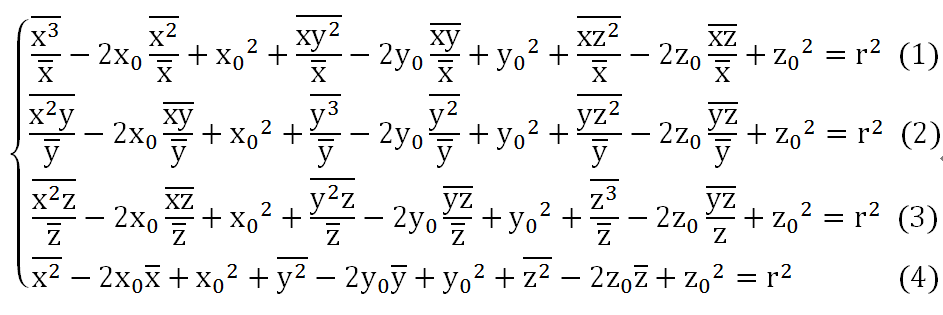
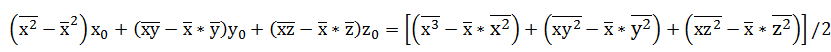
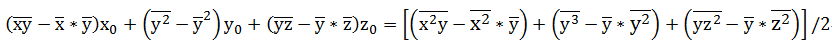
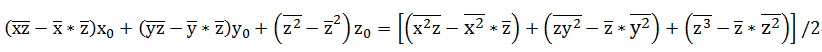
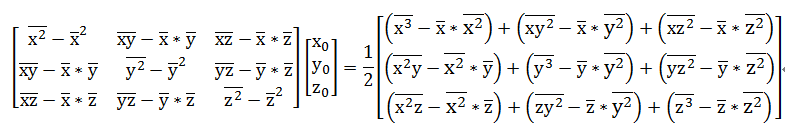






























 5003
5003

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








