构建整车七自由度模型

最新推荐文章于 2025-03-08 07:53:27 发布

是启军啊

最新推荐文章于 2025-03-08 07:53:27 发布

阅读量1.3w

点赞数 21

分类专栏：整车模型构建文章标签： matlab

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/wqj5211314/article/details/127234691

版权

整车模型构建专栏收录该内容

2 篇文章

订阅专栏

首先汽车七自由度模型包括车身的横摆，纵向和侧向，以及四个车轮的转动。

这里主要用到了车身坐标系x-y；和大地坐标系X-Y。

一、首先计算在车身坐标系下，汽车的纵向和侧向的加速度：

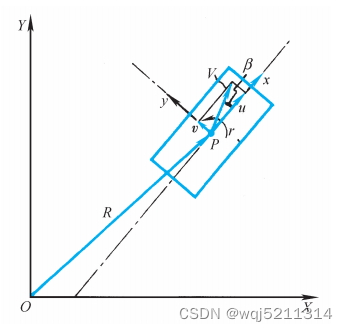
图1. 汽车运动时车身坐标系和大地坐标系的关系

这里的汽车的纵向速度为u，侧向速度为v

$\dot{R}= u\ast i+v\ast j$ （1）

两边求导可得

$\ddot{R}=\dot{u}*i+u*\dot{i}+\dot{v}*j+v*\dot{j}$ （2）

这里主要解决 $\dot{i}$ ， $\dot{j}$ 就可以求出纵向和侧向的加速度了；

方法1：

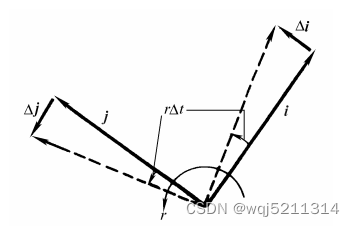
图2. 车身坐标系的变化

这里的变化可以看成在一个微小时间段的变化：可以得出

$\Delta i=r*\Delta t*j; \Delta j=-r*\Delta t*i;$ （3）

（3）两边同时除以 $\Delta t$ 在求极限可以得出

$\dot{i}=r*j;\dot{j}=-r*i;$ (4)

带入（2）中整理可得

$\ddot{R}=\left ( \dot{u}-v*r \right )*i+\left ( \dot{v}+u*r \right )*j;$ （5）

方法2、

图3.车身坐标系和大地坐标系的相对位置

其中 $\theta$ 为车辆横摆角，r为横摆角速度

有上图可以得出坐标转换公式为

$i=i_{F}*cos(\theta )+j_{F}*sin(\theta); j=-i_{F}*sin(\theta)+j_{F}*cos(\theta);$ (6)

对了（6）两边求导后可得到（4），之后即可得到（5）

二、整车模型公式

1.车身纵向、横向和横摆的平衡方程

图4.汽车简化模型

纵向力平衡：

$m*(\dot{u}-v*r)=(F_{xfl}+F_{xfr})*cos(\delta )-(F_{yfl}+F_{yfr})*sin(\delta )+F_{xrl}+F_{xrr}$

侧向力平衡：

$m*(\dot{v}+u*r)=(F_{xfl}+F_{xfr})*sin(\delta )+(F_{yfl}+F_{yfr})*cos(\delta)+F_{yrl}+F_{yrr}$

绕Z轴转矩平衡：

$I_{z}*\dot{r}=((F_{yfl}+F_{yfr})*cos(\delta)+(F_{xfl}+F{xfr})*sin(\delta))*a-(F_{yrl}+F_{yrr})*b+((F_{xfr}-F{xfl})*cos(\delta)+(F_{yfl}-F_{yfr})*sin(\delta))*\frac{t_{w1}}{2}+(F_{yrr}-F_{yrl})*\frac{t_{w2}}{2}$

其中 $I_{z}$ 为整车绕Z轴的转动惯量，a为汽车的前轴距，b为汽车的后轴距， $t_{w1}$ 为前轮距， $t_{w2}$ 为后轮距， $\delta$ 为方向盘转角， $F_{ijk}$ 为轮胎受力（i=x,y,z分别表示纵向，侧向力,垂向力；j=f,r表示前后，k=l,r表示左右）。

2.垂直载荷的计算

垂直载荷由三部分组成，静载荷和动载荷（前后载荷转移和左右载荷转移）

$F_{zfl}=\frac{mgb}{2l}-\frac{mh_{g}(\dot{u}-vr)}{2l}-\frac{mh_{g}(\dot{v}+ur)b}{t_{w1}l}$

$F_{zfr}=\frac{mgb}{2l}-\frac{mh_{g}(\dot{u}-vr)}{2l}+\frac{mh_{g}(\dot{v}+ur)b}{t_{w1}l}$

$F_{zrl}=\frac{mga}{2l}+\frac{mh_{g}(\dot{u}-vr)}{2l}-\frac{mh_{g}(\dot{v}+ur)a}{t_{w2}l}$

$F_{zrr}=\frac{mga}{2l}+\frac{mh_{g}(\dot{u}-vr)}{2l}+\frac{mh{g}(\dot{v}+ur)a}{t_{w2}l}$

3.各个轮胎侧偏角的计算：

$\alpha _{fl}=\delta-arctan \frac{v+ar}{u-\frac{t_w1}{2}r}$

$\alpha _{fr}= \delta - arctan \frac{v+ar}{u+ \frac{t_{w1}}{2}r}$

$\alpha_{rl} = -arctan \frac{v-br}{u- \frac{t_{w2}}{2}r}$

$\alpha_{rr}= -arctan \frac{v-br}{u+ \frac{t_{w2}}{2}r}$

这里的计算推到过程：假设车辆是刚体，轮胎速度包括车身的速度和轮胎绕质心旋转的速度，可以得出前左轮的纵向速度为 $u- \frac{t_{w1}}{2}r$ ，侧向速度为 $v+ar$ ,而车辆实际运动方向为 $\delta- \alpha_{fl}$ ,通过公式变换即可得到 $\alpha_{fl}$ ,其他同理可得。

4.各个车轮轮心的纵向速度：

$V_{T_{fl}}=(u- \frac{t_{w1}}{2}r)*cos(\delta)+(v+ar)*sin(\delta)$

$V_{T_{fr}}= (u+ \frac{t_{w1}}{2}r)*cos(\delta)+(v+ar)*sin(\delta)$

$V_{T_{rl}}= u- \frac{t_{w2}}{2}r$

$V_{T_{rr}}=u+ \frac{t_{w2}}{2}r$

5.轮胎滑移率的计算：

$\lambda _{fl}= \frac{W_{fl}R-V_{T_{fl}}}{V_{T_{fl}}}$

$\lambda_{fr}= \frac{W_{fr}R-V_{T_{fr}}}{V_{T_{fr}}}$

$\lambda_{rl}= \frac{W_{rl}R-V_{T_{rl}}}{V_{T_{rl}}}$

$\lambda_{rr}=\frac{W_{rr}R-V_{T_{rr}}}{V_{T_{rr}}}$

最后是魔术轮胎的建模，这里我单独发了一篇写魔术轮胎

三、整车模型模块化输入输出

图5.各变量输入输出关系

整车模型的构建按照上述公式在simulink中搭建好模块后进行输入输出的连接即可。

四、结果说明

这里的车辆工况是在1s后方向盘瞬间转角80度，车辆以50km\h的速度行驶。

一个七自由度模型输出结果包括：方向盘转角，横摆角速度，质心侧偏角，侧向加速度，四轮轮胎侧偏角，行驶轨迹。结果如下图所示

图6. 方向盘转角

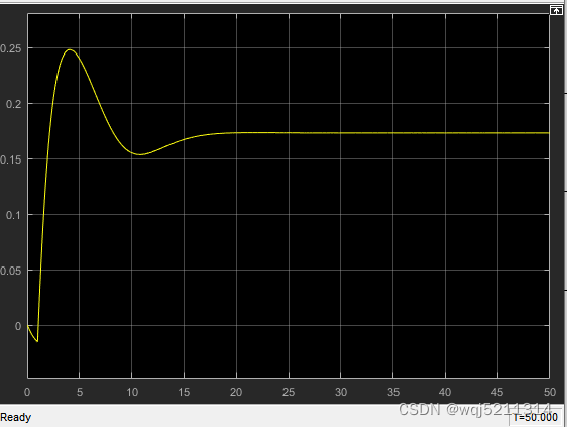
图7. 横摆角速度

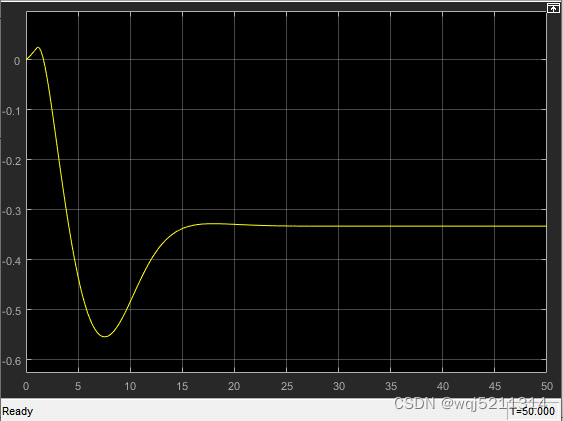
图8. 质心侧偏角

说明： $\beta =arctan \frac{u}{v}\approx \frac{u}{v}$ 在 $\beta$ 角较小时成立

图9. 侧向加速度

图10. 四轮轮胎侧偏角

图11. 汽车行驶轨迹图

这里的行驶轨迹的求解由图3可以得出：

$\dot{X}=ucos(\theta)-vsin(\theta)$

$\dot{Y}=usin(\theta)+vcos(\theta)$

五、建模注意事项

1.在垂直载荷的输入是，注意和魔术轮胎要求的垂直载荷单位一致；

2.方向盘转角的输入，必须乘以相应的转速比，比进行角度和弧度的换算；

六、参考文献；

(3条消息) 七自由度车辆稳定性数学模型和simulink求解_studyer_domi的博客-CSDN博客_七自由度车辆动力学模型

七自由度车辆模型浅谈 - 知乎 (zhihu.com)

车辆操作动力学理论与应用

声明：本文的撰写仅作为学习，转载标明出处。

评论 28

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。