参考may佬《技术美术百人计划》
拓展知识!!!矩阵的运用
图形1.2.2 矩阵运算
线性代数
一次方程为线性方程,具有可加性和比例性
- 可加性: f ( x 1 + x 2 ) = f ( x 1 ) + f ( x 2 ) f(x_1+x_2)=f(x_1)+f(x_2) f(x1+x2)=f(x1)+f(x2)
- 比例性: f ( k x ) = k f ( x ) f(kx)=kf(x) f(kx)=kf(x)
线性空间:直线变换后依旧是直线,并且等比;坐标原点保持不变

- 非线性空间:空间扭曲、非等距、原点位移
矩阵的定义
什么是矩阵
由 m × n m\times n m×n个数 a i j ( i = 1 , 2 , . . . m ; j = 1 , 2 , . . . n ) a_{ij}(i=1,2,...m;j=1,2,...n) aij(i=1,2,...m;j=1,2,...n)排组成的m行n列的数表称为m行n列的矩阵,简称 m × n m\times n m×n矩阵。
A = [ a 1 , 1 a 1 , 2 ⋯ a 1 , n a 2 , 1 a 2 , 2 ⋯ a 2 , n ⋮ ⋮ ⋱ ⋮ a m , 1 a m , 2 ⋯ a m , n ] A=\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \\ \end{bmatrix} A=⎣⎢⎢⎢⎡a1,1a2,1⋮am,1a1,2a2,2⋮am,2⋯⋯⋱⋯a1,na2,n⋮am,n⎦⎥⎥⎥⎤
解线性方程组
矩阵最开始用作解线性方程组
{ 2 x + 3 y = 1 x + y = 2 \begin{cases} 2x+3y=1\\ x+y=2\\ \end{cases} {2x+3y=1x+y=2
提取未知数,写成矩阵和向量的形式
[ 2 3 1 1 ] [ x y ] = [ 1 2 ] \begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} 1 \\ 2 \end{bmatrix} [2131][xy]=[12]
其中 A = [ 2 3 1 1 ] A=\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix} A=[2131]是矩阵, x ⃗ = [ x y ] \vec x=\begin{bmatrix}x \\ y \end{bmatrix} x=[xy] b ⃗ = [ 1 2 ] \vec b=\begin{bmatrix}1 \\ 2 \end{bmatrix} b=[12]是向量。
通过这种方法将线性方程组转化成向量方程,在已知矩阵 A A A和向量 b ⃗ \vec b b的情况下求未知向量 x ⃗ \vec x x
以矩阵方式解线性方程组
{ 2 x + 3 y = 1 x + y = 2 \begin{cases} 2x+3y=1\\ x+y=2\\ \end{cases} {2x+3y=1x+y=2
隐藏 x y xy xy,将等号右边的数字提出来,形成增广矩阵
[ 2 3 1 1 1 2 ] \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & 2 \\ \end{bmatrix} [213112]
每行可以单独乘系数或者每行相加减
[ 2 3 1 1 1 2 ] \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & 2 \\ \end{bmatrix} [213112] r 2 ′ = r 1 − 2 r 2 r_2'=r_1-2r_2 r2′=r1−2r2得到 [ 2 3 1 0 1 − 3 ] \begin{bmatrix} 2 & 3 & 1 \\ 0 & 1 & -3 \\ \end{bmatrix} [20311−3]
[ 2 3 1 0 1 − 3 ] \begin{bmatrix} 2 & 3 & 1 \\ 0 & 1 & -3 \\ \end{bmatrix} [20311−3] r 1 ′ = 1 2 ( r 1 − 3 r 2 ′ ) r_1'=\frac{1}{2}(r_1-3r_2') r1′=21(r1−3r2′)得到 [ 1 0 5 0 1 − 3 ] \begin{bmatrix} 1 & 0 & 5 \\ 0 & 1 & -3 \\ \end{bmatrix} [10015−3]
[ 1 0 5 0 1 − 3 ] \begin{bmatrix} 1 & 0 & 5 \\ 0 & 1 & -3 \\ \end{bmatrix} [10015−3]等同于 { x + 0 y = 5 0 x + y = − 3 \begin{cases} x+0y=5\\ 0x+y=-3\\ \end{cases} {x+0y=50x+y=−3 得出 x = 5 x=5 x=5, y = 3 y=3 y=3
矩阵变换
通过列空间去理解矩阵变换的意义

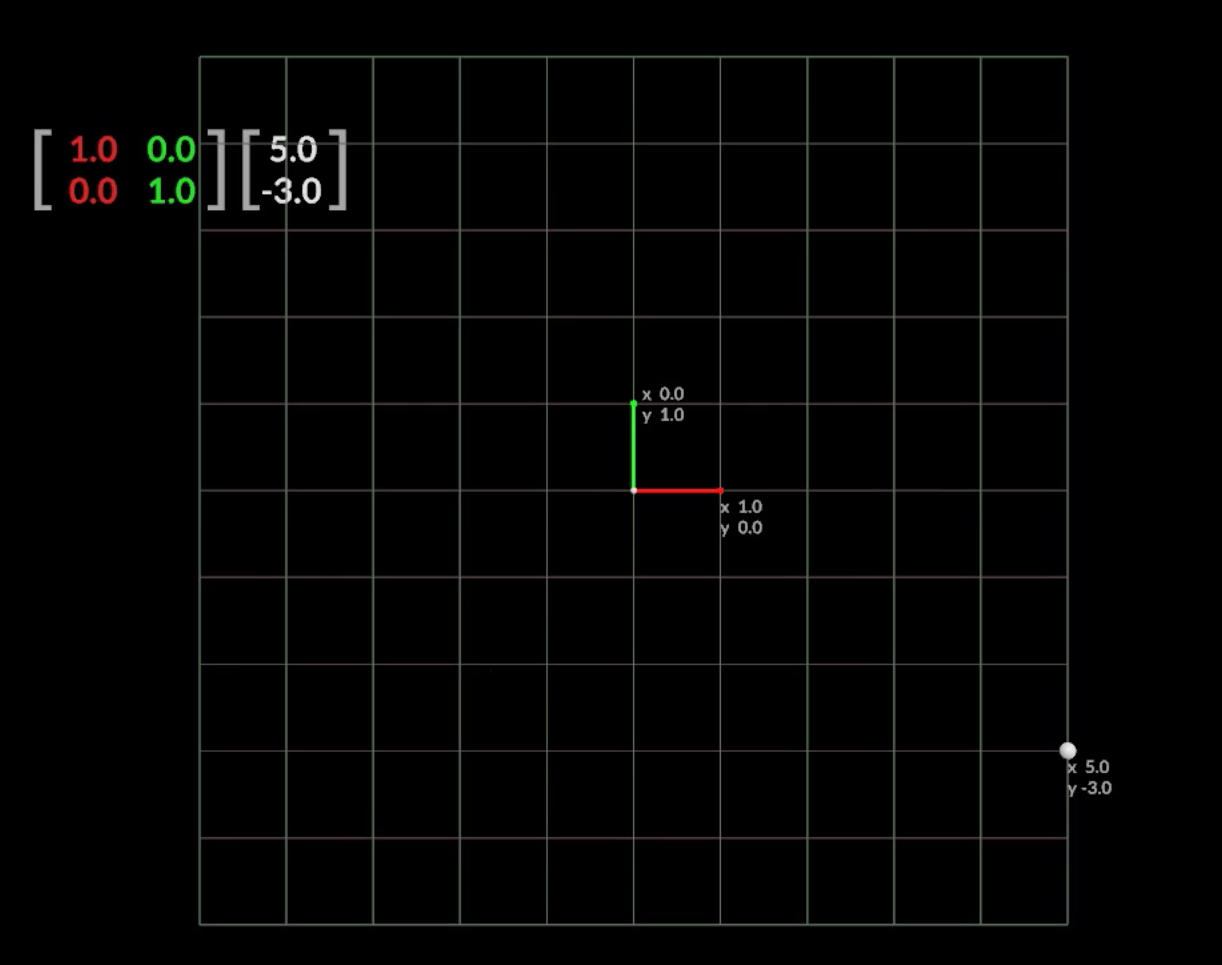
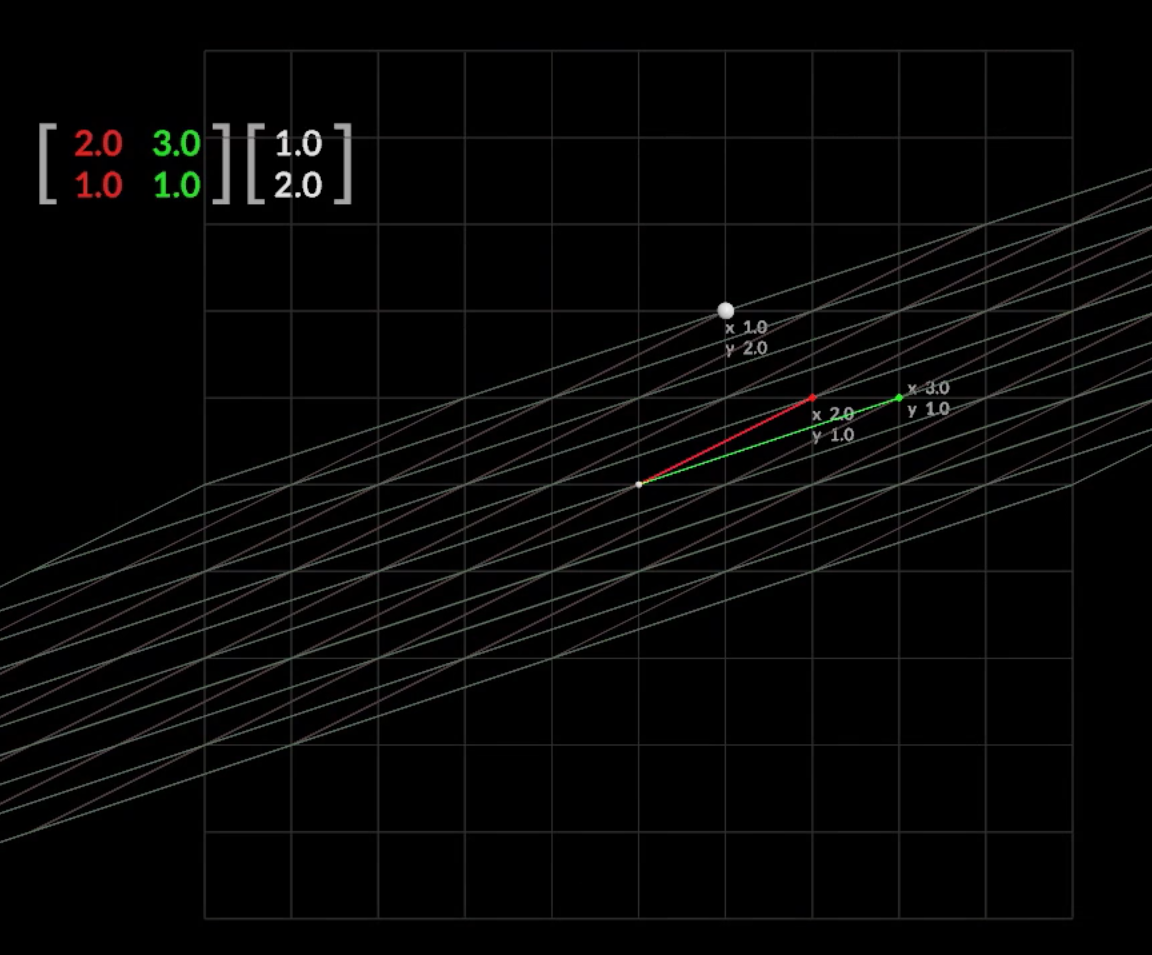
特殊矩阵
- 方阵: 行列数均等于n的矩阵被称为n阶矩阵或n阶方阵
- [ 1 2 3 4 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} [1324] 二阶方阵
- [ 1 2 3 4 5 6 7 8 9 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} ⎣⎡147258369⎦⎤ 三阶方阵
- 单位矩阵: n×n矩阵,对角线元素为1,其余为0
- [ 1 0 0 1 ] \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} [1001] 二阶单位矩阵
- [ 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} ⎣⎡100010001⎦⎤ 三阶单位矩阵
- 零矩阵:元素都是0的矩阵
- [ 0 0 0 0 ] \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ \end{bmatrix} [0000] 二阶零矩阵
- [ 0 0 0 0 0 0 0 0 0 ] \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} ⎣⎡000000000⎦⎤ 三阶零矩阵
矩阵运算
矩阵加法
- 对应位置相加
- 只有行数列数都相等的同型矩阵才能进行加减运算
- [ 1 2 3 4 ] + [ 4 3 2 1 ] = [ 1 + 4 2 + 3 3 + 2 4 + 1 ] = [ 5 5 5 5 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}+\begin{bmatrix} 4 & 3 \\ 2 & 1 \\ \end{bmatrix}=\begin{bmatrix} 1+4 & 2+3 \\ 3+2 & 4+1 \\ \end{bmatrix}=\begin{bmatrix} 5 & 5 \\ 5 & 5 \\ \end{bmatrix} [1324]+[4231]=[1+43+22+34+1]=[5555]
- 满足交换律和结合律
- A + B = B + A A+B=B+A A+B=B+A
- ( A + B ) + C = A + ( B + C ) (A+B)+C=A+(B+C) (A+B)+C=A+(B+C)
- 减法: A − B = A + ( − B ) A-B=A+(-B) A−B=A+(−B)
矩阵数乘
- 常数 k k k与矩阵 A A A的每一项相乘,乘积为矩阵,记作 k A kA kA
- k A = A k = [ k a 1 , 1 k a 1 , 2 ⋯ k a 1 , n k a 2 , 1 k a 2 , 2 ⋯ k a 2 , n ⋮ ⋮ ⋱ ⋮ k a m , 1 k a m , 2 ⋯ k a m , n ] kA=Ak=\begin{bmatrix} ka_{1,1} & ka_{1,2} & \cdots & ka_{1,n} \\ ka_{2,1} & ka_{2,2} & \cdots & ka_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ ka_{m,1} & ka_{m,2} & \cdots & ka_{m,n} \\ \end{bmatrix} kA=Ak=⎣⎢⎢⎢⎡ka1,1ka2,1⋮kam,1ka1,2ka2,2⋮kam,2⋯⋯⋱⋯ka1,nka2,n⋮kam,n⎦⎥⎥⎥⎤
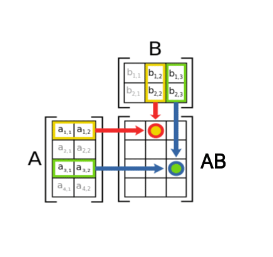
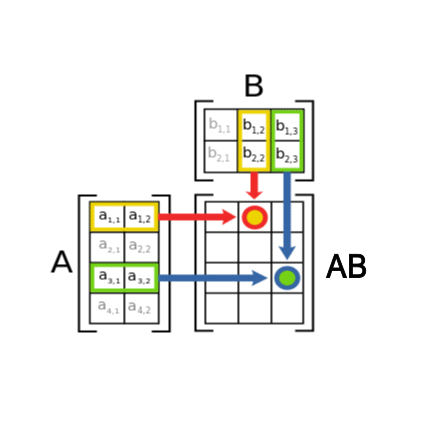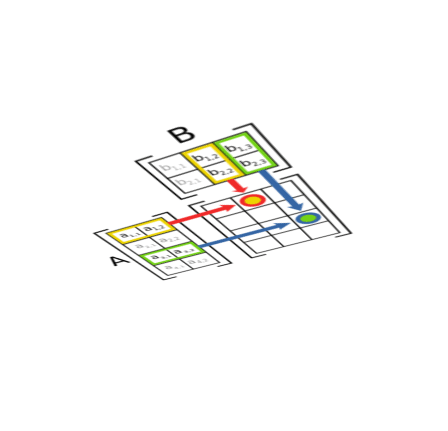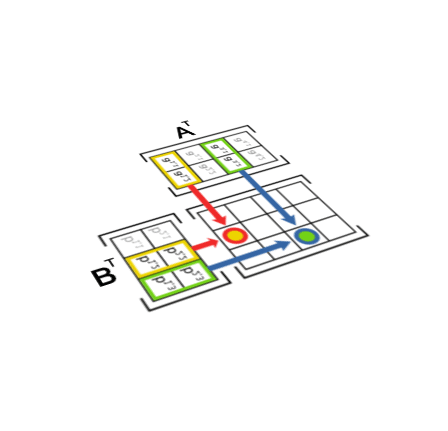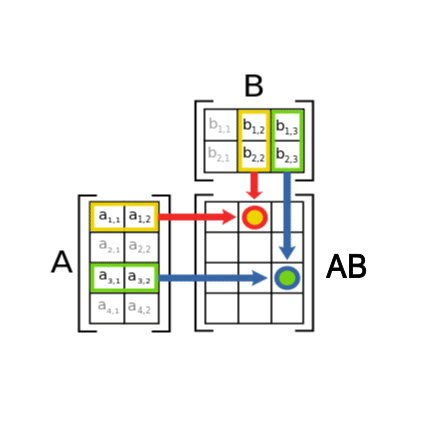
矩阵乘法
-
m×n的矩阵只能和n×p的矩阵相乘,结果为m×p的矩阵(前行乘后列)
-
[ 2 1 0 3 5 4 ] × [ 7 6 8 9 ] = [ ( 2 , 1 ) ⋅ ( 7 , 8 ) 2 × 6 + 1 × 9 0 × 7 + 3 × 8 0 × 6 + 3 × 9 5 × 7 + 4 × 8 5 × 6 + 4 × 9 ] \begin{bmatrix} 2 & 1 \\ 0 & 3 \\ 5 & 4\end{bmatrix}\times\begin{bmatrix} 7 & 6 \\ 8 & 9 \\ \end{bmatrix}=\begin{bmatrix} (2,1)·(7,8) & 2\times6+1\times9 \\ 0\times7+3\times8 & 0\times6+3\times9 \\ 5\times7+4\times8 & 5\times6+4\times9 \end{bmatrix} ⎣⎡205134⎦⎤×[7869]=⎣⎡(2,1)⋅(7,8)0×7+3×85×7+4×82×6+1×90×6+3×95×6+4×9⎦⎤
-
几何意义:矩阵×矩阵=矩阵,矩阵×向量=向量
-
复合变换左乘

-
运算律
- 交换律 不一定满足
- 数乘交换律 k ( A B ) = ( k A ) B = A ( k B ) k(AB)=(kA)B=A(kB) k(AB)=(kA)B=A(kB)
- 结合率 ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
- 分配律 A ( B + C ) = A B + A C A(B+C)=AB+AC A(B+C)=AB+AC
-
常见矩阵

- 位移矩阵是仿射变换,不是线性变换(原点改变)
-
三维空间的坐标变换
- 缩放矩阵 [ x 0 0 0 0 y 0 0 0 0 z 0 0 0 0 1 ] \begin{bmatrix} x & 0 & 0 & 0 \\ 0 & y & 0 & 0 \\ 0 & 0 & z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡x0000y0000z00001⎦⎥⎥⎤
- 绕x轴旋转矩阵 [ 1 0 0 0 0 cos θ − sin θ 0 0 sin θ cos θ 0 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0 \\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡10000cosθsinθ00−sinθcosθ00001⎦⎥⎥⎤
- 绕y轴旋转矩阵 [ cos θ 0 sin θ 0 0 1 0 0 − sin θ 0 cos θ 0 0 0 0 1 ] \begin{bmatrix} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡cosθ0−sinθ00100sinθ0cosθ00001⎦⎥⎥⎤
- 绕z轴旋转矩阵
[
cos
θ
−
sin
θ
0
0
sin
θ
cos
θ
0
0
0
0
1
0
0
0
0
1
]
\begin{bmatrix} \cos \theta & -\sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
⎣⎢⎢⎡cosθsinθ00−sinθcosθ0000100001⎦⎥⎥⎤
- unity中的旋转顺序是z-x-y
- 位移矩阵 [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡100001000010txtytz1⎦⎥⎥⎤
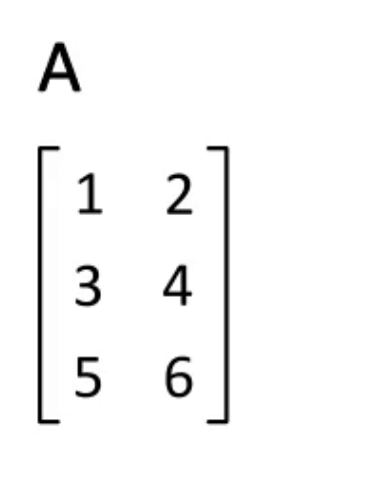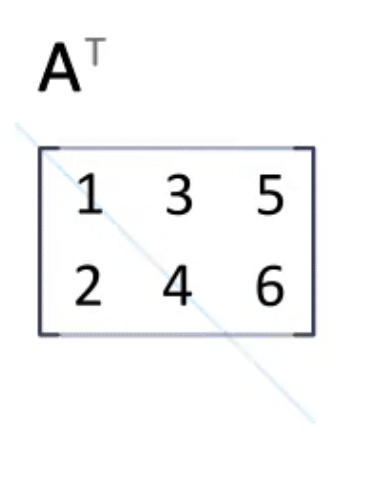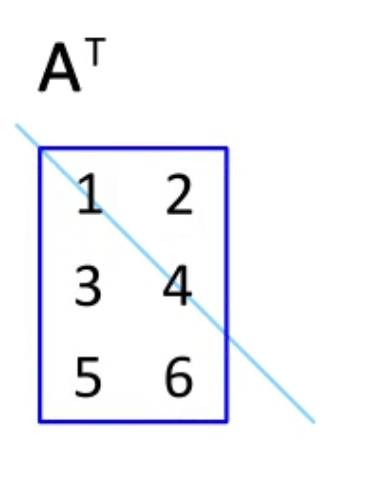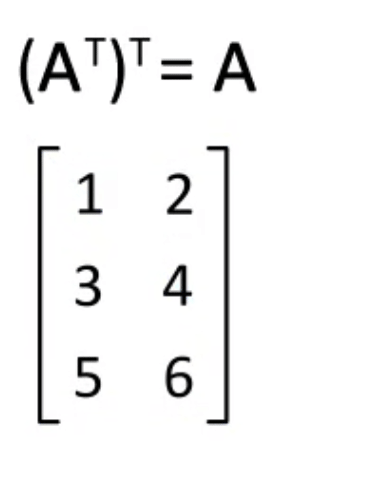
矩阵转置
将矩阵的行和列进行互换, A A A转置后得到的转置矩阵记作 A T A^T AT
-
A = ( a i , j ) , A T = ( a j , i ) A=(a_{i,j}),A^T=(a_{j,i}) A=(ai,j),AT=(aj,i)
-
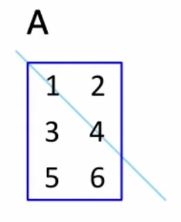
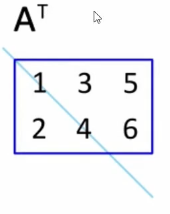
-
运算性质
-
( A T ) T = A (A^T)^T=A (AT)T=A
-
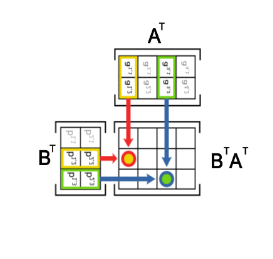
( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
-
( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
-
矩阵的逆
矩阵与逆矩阵相乘得到单位矩阵
- I = A A − 1 = A − 1 A I=AA^{-1}=A^{-1}A I=AA−1=A−1A
- 常用作矩阵变换之后再次矩阵变换回原来的初始位置

- 运算规律
- 若 A A A可逆,则 A − 1 A^{-1} A−1也可逆, ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
- 若 A A A可逆,数 λ ≠ 0 \lambda\not=0 λ=0,则 λ A \lambda A λA可逆, ( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1}=\frac{1}{\lambda}A^{-1} (λA)−1=λ1A−1
- 若 A 、 B A、B A、B为同阶矩阵且均可逆,则 A B AB AB也可逆, ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
- 若 A A A可逆,则 A T A^T AT也可逆, ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T






















 279
279











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








