TA入门笔记（四）

参考may佬《技术美术百人计划》
冯乐乐《Unity Shader入门精要》
写给VR手游开发小白的教程：（四）补充篇，详细介绍Unity中相机的投影矩阵
投影矩阵的推导(Deriving Projection Matrices)
Eric Lengyel. Mathematics for 30 game programming and computer graphics (3rd Edition). 2011 by Charles River Media

图形1.2.3 MVP矩阵变换

变换矩阵

• 将3D物体转化到2D平面
• 为各个空间的运用做准备

MVP矩阵

MVP矩阵分别是模型（Model）矩阵、观察（View）矩阵、投影（Projection）矩阵。

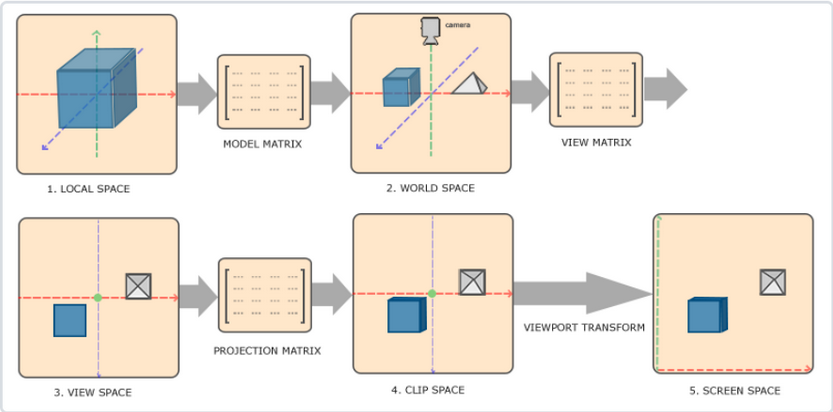
坐标空间

• 因为一些概念只有在特定的坐标空间下才有意义，才更容易理解，所以我们需要在不同的情况下使用不同的坐标空间。
• 顶点的起始坐标位于局部空间（模型空间），在这里被称作局部坐标（Local Coordinate），之后会变为世界坐标（World Coordinate）、观察坐标（View Coordinate）、裁剪坐标（Clip Coordinate），最后以屏幕坐标（Screen Coordinate）结束。
• 

M矩阵

模型空间$\to$世界空间

• 将顶点坐标从模型空间变换到世界空间的过程被称作模型变换
• 模型变换依次进行了缩放、旋转、平移的操作，对应操作依次进行矩阵变换即可得出模型变换的变换矩阵，即M矩阵(注意矩阵的左乘顺序）
• $M_{model}=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{k}_x& 0& 0& 0\\ 0& k_y& 0& 0\\ 0& 0& k_z& 0\\ 0& 0& 0& 1\end{array}\right]$
• $P_{world}=M_{model}{P}_{model}$

V矩阵

世界空间$\to$观察空间

• 将顶点坐标从世界空间变换到观察空间，被叫做观察变换
• 变换步骤：
  • 平移整个观察空间，让摄像机原点位于世界坐标的原点，坐标轴与世界空间中的坐标轴重合
  • 摄像机在世界空间中是先旋转再平移的，因此为了将摄像机移回初始状态（位于原点，坐标轴重合），需要进行逆变换
  • 在Unity中模型空间和世界空间都是左手系，观察空间却是右手系，z轴方向相反，因此需要对z取反
  • 所以观察变换的顺序为先平移，再旋转，最后对z分量取反
• $M_{view}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]$
• $P_{view}=M_{view}{P}_{world}$

P矩阵

观察空间$\to$裁剪空间

• 用于判断顶点是否在可见范围内，为投影做准备（虽然叫做投影变换，但是并没有真正进行投影工作）

• 位于视锥体内的图元保留，视锥体之外的图元将被剔除，与裁剪平面相交的图元会被裁剪

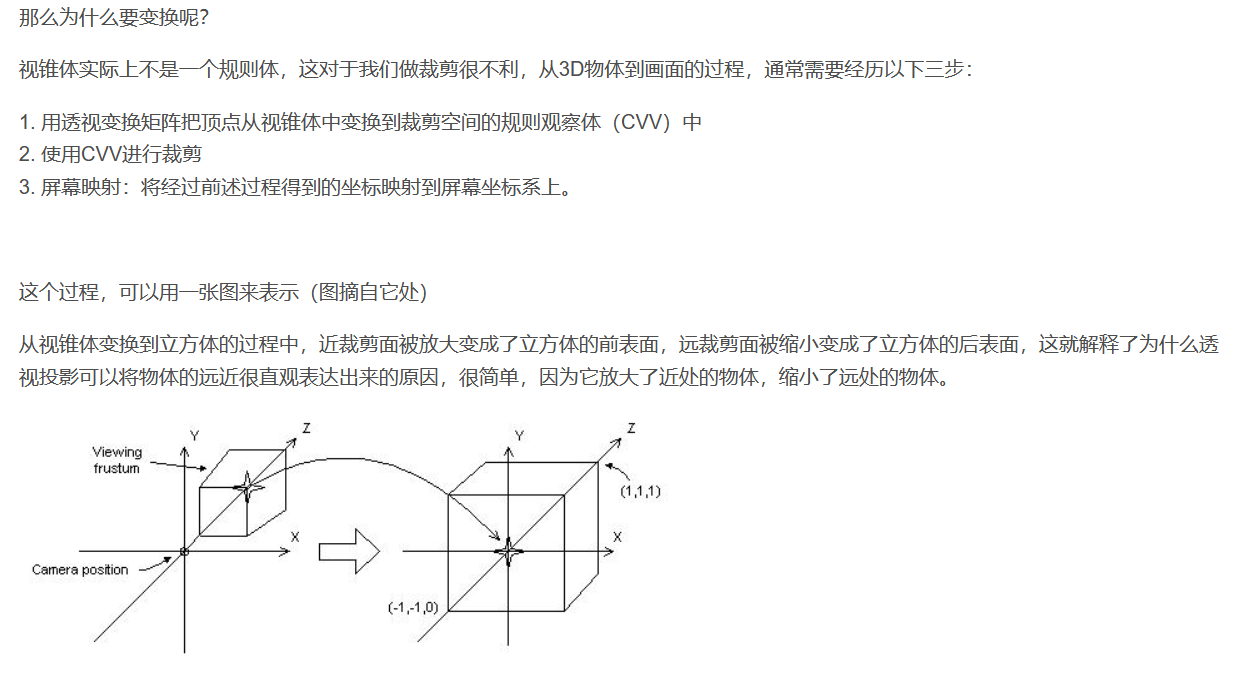
  • 为什么要进行投影变换？
    

• 透视投影
  

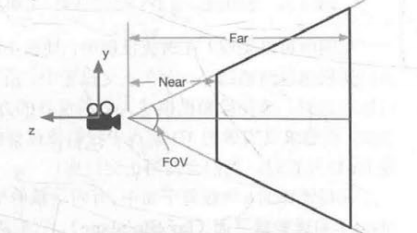
  • 根据Near和Far以及视场角FOV可以求出视锥体近裁剪平面和远裁剪平面的高度：
    • $nearClipPlaneHeight=2\cdot Near\cdot \tan \frac{FOV}{2}$
    • $farClipPlaneHeight=2\cdot Far\cdot \tan \frac{FOV}{2}$
  • 根据摄像机的纵横比Aspect得到裁剪平面的宽度
    • $Aspect=\frac{nearClipPlaneWidth}{nearClipPlaneHeight}$
    • $Aspect=\frac{farClipPlaneWidth}{farClipPlaneHeight}$
  • $M_{frustum}=\left[\begin{array}{cccc}\frac{\cot \frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& \cot \frac{FOV}{2}& 0& 0\\ 0& 0& -\frac{Far+Near}{Far-Near}& -\frac{2\cdot Near\cdot Far}{Far-Near}\\ 0& 0& -1& 0\end{array}\right]$
  • $P_{clip}=M_{frustum}{P}_{view}=\left[\begin{array}{c}x\frac{\cot \frac{FOV}{2}}{Aspect}\\ y\cot \frac{FOV}{2}\\ -z\frac{Far+Near}{Far-Near}-\frac{2\cdot Near\cdot Far}{Far-Near}\\ -z\end{array}\right]$
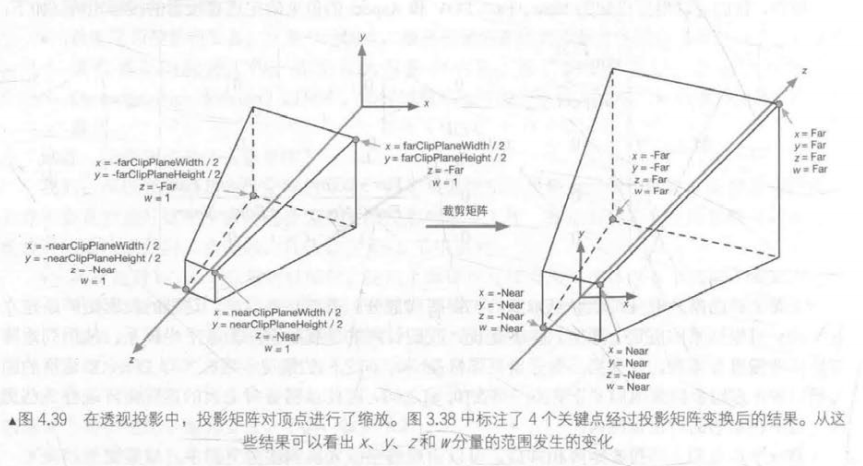
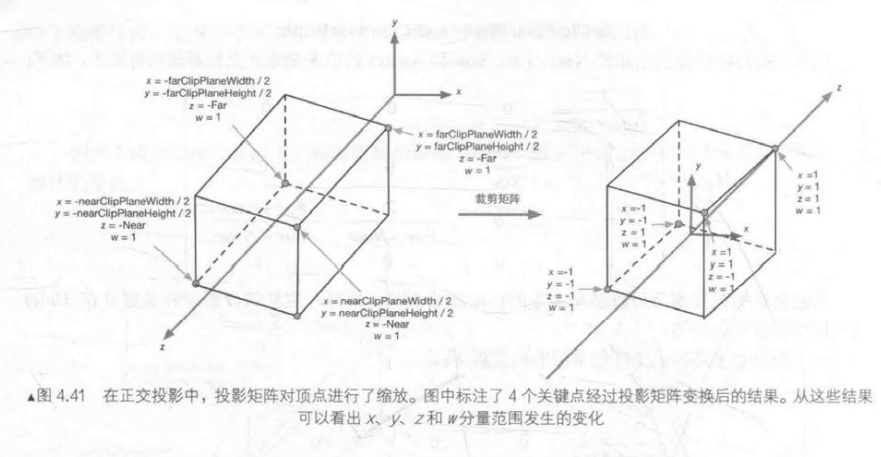
  • 可以看出，投影矩阵本质是对$x$、$y$、$z$分量进行了不同程度的缩放（同时对$z$分量进行了平移），此时顶点的$w$分量不再是1，而是原先$z$分量的取反。
  • 如果一个顶点在视锥体内，那么它变换后的坐标需满足：
    $-w\le x\le w$
    $-w\le y\le w$
    $-w\le z\le w$
    

• 正交投影
  

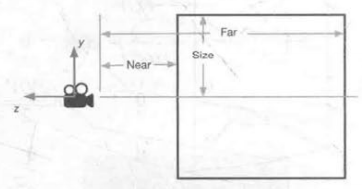
  • 根据Near和Far以及Size可以得到裁剪平面高度
    • $nearClipPlaneHeight=farClipPlaneHeight=2\cdot Size$
  • 根据摄像机纵横比Aspect得到裁剪平面宽度
    • $farClipPlaneWidth=nearClipPlaneWidth=Aspect\cdot nearClipPlaneHeight$
  • $M_{frustum}=\left[\begin{array}{cccc}\frac{1}{Aspect\cdot Size}& 0& 0& 0\\ 0& \frac{1}{Size}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& -\frac{Far+Near}{Far-Near}\\ 0& 0& 0& 1\end{array}\right]$
  • $P_{clip}=M_{ortho}{P}_{view}=\left[\begin{array}{c}\frac{x}{Aspect\cdot Size\cdot }\\ \frac{y}{Size}\\ -\frac{2z}{Far-Near}-\frac{Far+Near}{Far-Near}\\ 1\end{array}\right]$
  • 如果一个顶点在视锥体内，那么它变换后的坐标需满足：
    $-w\le x\le w$
    $-w\le y\le w$
    $-w\le z\le w$
    

P矩阵推导

先从正交投影开始
为了方便计算，定义视锥体的范围为从$(l,b,n)$到$(r,t,f)$

根据这张图可知，正交投影将视锥体的范围映射到（-1，-1，-1）至（1，1，1），即将三个坐标的范围变换至$[-1,1]$

从$x$轴开始

$l\le x\le r$

经过一系列变换将中间项变成形如$px+q$的形式

$0\le x-l\le r-l$

$-1\le \frac{2(x-l)}{r-l}-1\le 1$

$-1\le \frac{2x}{r-l}-\frac{r+l}{r-l}\le 1$

这个中间项即转换$x$的公式

$x^{\prime }=\frac{2x}{r-l}-\frac{r+l}{r-l}$

同理可得$y$的转换公式

$y^{\prime }=\frac{2y}{t-b}-\frac{t+b}{t-b}$

需要注意的是，视锥体经过转换之后从右手系转换到了左手系，因此$z$是从$[-f,-n]$映射到$[-1,1]$

tips:OpenGL的z分量映射到[-1,1]，DirectX的z分量则是映射到[0,1]

$-n\le z\le -f$

$-1\le -\frac{2z}{f-n}-\frac{f+n}{f-n}\le 1$

得到$z$的转换公式

$z^{\prime }=-\frac{2z}{f-n}-\frac{f+n}{f-n}$

w分量为1，此时的转换矩阵为

$P_o=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& -\frac{2z}{f-n}& -\frac{f+n}{f-n}\\ 0& 0& 0& 1\end{array}\right]$

由于z轴会穿过视锥体的中心，因此$r=-l,t=-b$，通过摄像机组件可以获得以下信息

$nearClipPlaneHeight=farClipPlaneHeight=2\cdot Size$

$farClipPlaneWidth=nearClipPlaneWidth=Aspect\cdot nearClipPlaneHeight$

代入之后可得到正交投影矩阵

$M_{frustum}=\left[\begin{array}{cccc}\frac{1}{Aspect\cdot Size}& 0& 0& 0\\ 0& \frac{1}{Size}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& -\frac{Far+Near}{Far-Near}\\ 0& 0& 0& 1\end{array}\right]$

接下来是透视投影，对$x,y$的处理可以分两步：

1. 给定视锥体中的点$(x,y,z)$，把它投影到近平面$z=n$。由于投影点在近平面上，所以它的$x$坐标范围在$[l,r]$，$y$坐标范围在$[b,t]$。
2. 使用在正交投影中推导的公式，把$x$坐标从$[l,r]$映射到$[-1,1]$，把$y$坐标范围从$[b,t]$映射到$[-1,1]$。

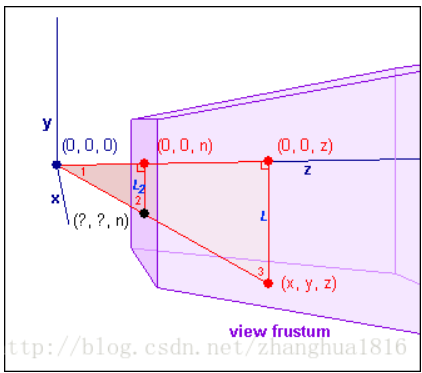
根据相似三角形，可知$x$坐标为$\frac{xn}{z}$，$y$坐标为$\frac{yn}{z}$

将以上坐标带入之前推导的公式中

$x^{\prime }=(\frac{2n}{r-l})\frac{x}{z}-\frac{r+l}{r-l}$

$y^{\prime }=(\frac{2n}{t-b})\frac{y}{z}-\frac{t+b}{t-b}$

消去分母上的$z$

$x^{\prime }z=(\frac{2n}{r-l})x-\frac{r+l}{r-l}z$

$y^{\prime }z=(\frac{2n}{t-b})y-\frac{t+b}{t-b}z$

为了将等式写入矩阵，需要转化成形如$x^{\prime }=c_{1}x+c_{2}y+c_{3}z+c_4$的格式，为此需要获得一个相似的$z^{\prime }z$的公式，然后就可以通过一个变换矩阵将$(x,y,z)$映射到$(x^{\prime }z,y^{\prime }z,z^{\prime }z)$,再将各部分除以$z$即可得到需要的$(x^{\prime },y^{\prime },z^{\prime })$

为此需要一个公式形如$z^{\prime }z=pz+q$，已知需要把$[-f,-n]$映射到$[-1,1]$因此当$z=-f$时$z^{\prime }=1$,$z=-n$时$z^{\prime }=-1$，可得方程组

tips：此处映射关系要注意，-f  , -n ---> -1  ,  1
					     |     |_______|     |
						 |___________________|

$-f=pf+q$
$n=pn+q$

解得$p=-\frac{f+n}{f-n},q=-\frac{2nf}{f-n}$

代入得到$z^{\prime }z=(-\frac{f+n}{f-n})z-\frac{2nf}{f-n}$

由于此时是在为点$(x^{\prime }z,y^{\prime }z,z^{\prime }z,w^{\prime }z)$做变换，所以把$w^{\prime }=1$写作$w^{\prime }z=z$,得到最终用于透视投影的等式为

$x^{\prime }z=(\frac{2n}{r-l})x-\frac{r+l}{r-l}z$

$y^{\prime }z=(\frac{2n}{t-b})y-\frac{t+b}{t-b}z$

$z^{\prime }z=(-\frac{f+n}{f-n})z-\frac{2nf}{f-n}$

$w^{\prime }z=z$

写成矩阵的形式为

$P_p=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& -\frac{r+l}{r-l}& 0\\ 0& \frac{2n}{t-b}& -\frac{t+b}{t-b}& 0\\ 0& 0& -\frac{f+n}{f-n}& -\frac{2nf}{f-n}\\ 0& 0& 1& 0\end{array}\right]$

根据摄像机组件获得以下信息

$nearClipPlaneHeight=2\cdot Near\cdot \tan \frac{FOV}{2}$
$farClipPlaneHeight=2\cdot Far\cdot \tan \frac{FOV}{2}$

$Aspect=\frac{nearClipPlaneWidth}{nearClipPlaneHeight}$
$Aspect=\frac{farClipPlaneWidth}{farClipPlaneHeight}$

最终求得透视投影矩阵为

$M_{frustum}=\left[\begin{array}{cccc}\frac{\cot \frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& \cot \frac{FOV}{2}& 0& 0\\ 0& 0& -\frac{Far+Near}{Far-Near}& -\frac{2\cdot Near\cdot Far}{Far-Near}\\ 0& 0& -1& 0\end{array}\right]$

坐标空间的应用