在matlab和python if中的旋转变换（四元数、欧拉角、旋转矩阵)等

目录

1. 基本的认识

空间中的坐标变换包括平移和旋转。

• 平移变换较为简单，只需要加上一个位置矢量即可。
• 旋转变换常见的有三种表示方式：旋转矩阵、欧拉角、四元数。

注：由于博主本人知识有限以及篇幅的缘故，博文十分简略，阅读本篇博客前需要一定的知识基础，有问题欢迎一起交流讨论。

2. 变换矩阵

根据《机器人学导论》，我们用平移算子${}^A{P}_{BO}$和旋转算子${}_B^{A}R$进行变换矩阵的计算。
$${\left[\begin{array}{c}{}^{A}P\\ 1\end{array}\right]}_{4\times 1}={\left[\begin{array}{cc}{}_B^{A}R& {}^A{P}_{BO}\\ \text{0}& 1\end{array}\right]}_{4\times 4}{\left[\begin{array}{c}{}^{B}P\\ 1\end{array}\right]}_{4\times 1}$$

1. 平移算子${}^A{P}_{BO}$
   平移将空间中的一个点沿着一个已知的矢量方向移动一定距离。
   $${}^A{P}_{BO}={\left[\begin{array}{c}{q}_x\\ q_y\\ q_z\end{array}\right]}_{3\times 1}$$

2. 旋转算子${}_B^{A}R$
   通常是绕坐标系的x、y、z轴旋转一定角度的旋转算子，遵循右手旋转法则。
   例如：绕z轴旋转$\theta$角度的算子：
   $${}_B^{A}R={\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]}_{3\times 3}$$
   具体原理的话可以参考原书，也可以参考原理，公式。

3. 欧拉角

欧拉角用三个数描述从一个坐标系到另一个坐标系的变换，每个数分别是绕某一个坐标轴转动的角度。网上对于欧拉角对应坐标轴的名称不是很统一，这里参考维基百科，所指的欧拉角是偏航、俯仰和滚转（yaw, pitch and roll），分别对应z,y,x轴的转角。
通常的欧拉角是intrinsic rotations，又称内在旋转，动态旋转等，每次旋转参照的坐标系是旋转后的新坐标系，也可以理解为刚体坐标系。而还有一种欧拉角是extrinsic rotations，又称固定角，外在旋转，静态旋转等，每次旋转参照的坐标系是原始的固定坐标系，两者存在一一对应的关系，以下摘自维基百科：

三个基本旋转可以围绕原始坐标系的轴发生，它保持不动（extrinsic rotations，外在旋转），或者围绕旋转坐标系的轴，在每次基本旋转后改变其方向（intrinsic rotations，内在旋转）。

为 Tait-Bryan 角选择旋转轴有六种可能性。六个可能的序列是：

• x - y ′- z ″（内在旋转）或z - y - x（外在旋转）
• y - z ′- x ″（内在旋转）或x - z - y（外在旋转）
• z - x ′- y ″（内在旋转）或y - x - z（外在旋转）
• x - z ′- y ″（内在旋转）或y - z - x（外在旋转）
• z - y ′- x ″（内在旋转）或x - y - z（外在旋转）：内在旋转称为：偏航、俯仰和滚转（ypr）
• y - x ′- z ″（内在旋转）或z - x - y（外在旋转）

具体原理可以参考知乎问题。

4. 四元数

个人理解，某种意义上可以把四元数类比于复数，同样具有实部虚部，同样具有直角坐标形式和极坐标意义，只是把复平面拓展到了“复空间”中。
四个数分别是实部w，虚部x，y，z。在matlab中顺序为wxyz，tf库中顺序为xyzw。四元数的逆等于共轭除以模。作为旋转的四元数是单位四元数：模为1，逆和共轭相等。
具体原理请参照这个知乎回答，简洁明了，超赞！

5. matlab中相互转换

matlab中有相应的转换函数。
注意，在这里欧拉角为弧度制，四元数顺序为wxyz，欧拉角是内旋的欧拉角，默认旋转顺序为zyx，旋转矩阵为三行三列，并且对旋转矩阵进行转置才可以乘以通常的列向量位置矢量。

注释	函数
欧拉角到四元数	q = angle2quat(r1, r2, r3, s), s默认是ZYX顺序，即’ZYX’
矩阵到四元数	q = dcm2quat(n)
四元数到欧拉角	[r1 r2 r3] = quat2angle(q, s)
矩阵到欧拉角	[r1 r2 r3] = dcm2angle(n, s)
四元数到矩阵	n = quat2dcm(q)
固定角到矩阵	n = angle2dcm(r1, r2, r3, s)

6. python tf中相互转换

使用tf库需要安装tf库并在文件开头import tf，这里参考的是一篇tf笔记
注意，下面的函数前需加 tf.transformations. ，这里为了表格美观而省略了。四元数顺序为xyzw，欧拉角是外旋的固定角，默认旋转顺序为xyz。矩阵维度是44，包括旋转和平移变换，旋转变换取前33即可。

注释	函数
固定角到四元数	quaternion_from_euler(ai,aj,ak,axes=‘sxyz’)
矩阵到四元数	quaternion_from_matrix(matrix)
四元数到固定角	eular_from_quaternion(quaternion,axes=‘sxyz’)
矩阵到欧拉角	eulaer_from_matrix(matrix,axes=‘sxyz’)
四元数到矩阵	quaternion_matrix(quaternion)
固定角到矩阵	euler_matrix(ai,aj,ak,axes=‘sxyz’)

7. 一点补充及疑惑

疑惑应该是解决了。
原本博主以为matlab中是采用通常的欧拉角进行变换，但在实际测试中发现，matlab中采用q = angle2quat(r1, r2, r3, ‘zyx’)进行计算和python中采用tf.transformations.quaternion_form_euler(ai,aj,ak,axes=‘szyx’)进行计算，两者对同样的欧拉角计算得到的四元数并不相同
然后博主通过欧拉角和旋转矩阵的对应关系对此进行验证：
假设欧拉角为（1.57, 0, 0），
根据欧拉角旋转矩阵公式：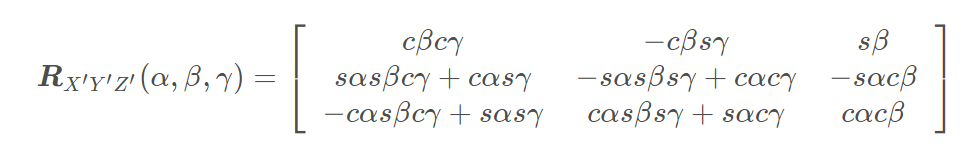

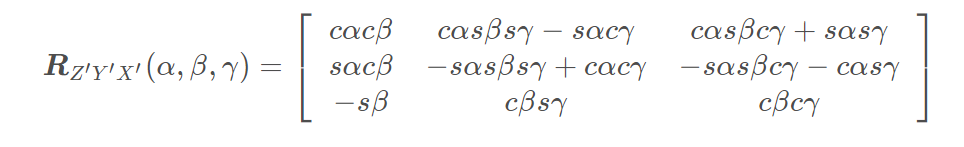
可以得到：
$$R_{XYZ}={\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right]}_{3\times 3}，R_{ZYX}={\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]}_{3\times 3}$$
在matlab中：
运行n = angle2dcm(1.57, 0, 0，‘xyz’)和n = angle2dcm(1.57, 0, 0，‘zyx’)，得到结果：
$$n_{XYZ}={\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right]}_{3\times 3}，n_{ZYX}={\left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 1\end{array}\right]}_{3\times 3}$$
在python tf中：
运行

import tf
n = tf.transformations.euler_matrix(ai,aj,ak,axes=‘sxyz’)
print(n)
n = tf.transformations.euler_matrix(ai,aj,ak,axes=‘szyx’)
print(n)

可以得到：
$$n_{XYZ}={\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right]}_{3\times 3}，n_{ZYX}={\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]}_{3\times 3}$$
注：实际结果中n为$4\times 4$变换矩阵，这里提取其中的$3\times 3$旋转矩阵。
对比结果可知，python中的转换函数符合和旋转矩阵的对应关系，而matlab不符合。对这个结博主还没搞清楚是为什么，只能初步下结论：python的转换结果是准确的。

在C++中也可以使用tf库，参考本链接

这是博主的第一篇博客，作为菜鸟，一直都是参照网上的教程学习，但是自己做的笔记十分的乱，在onenote、ipad、anki上都有，查找和阅读体验都十分的差，因此有了用博客的方式来系统记录和整理笔记的想法，并且在花费了半天的时间之后，终于诞生了这一篇博客。虽然内容十分简略，但总归是开始行动了。
修改多次，还存在疑惑，欢迎一起讨论
最后，有问题欢迎一起交流讨论呀，祝大家都学业有成，生活顺利！