机器学习实战——Logistic回归

1 Logistic回归模型的介绍

逻辑斯蒂（Logistic）回归是指具有如下形式的函数模型：

$y=\frac{1}{1+e^{-z}}$

$z={\omega }^{T}x+b$

则 $y$ 的取值如下：

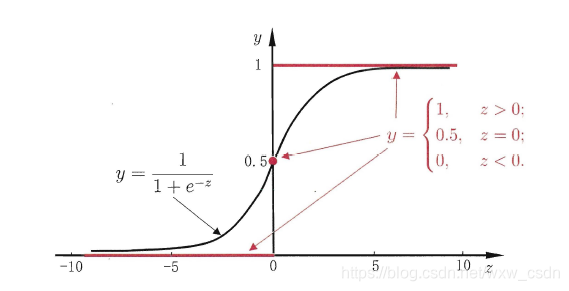
一个事件的几率是指该事件发生的概率与不发生的概率的比值。对于二分类事件，如果事件发生的概率为 $p$ ，不发生的概率为 $1-p$ ，则该事件的几率可以表示为 $\frac{p}{1-p}$ ，对该几率取对数可得 $\ln \frac{p}{1-p}$ 。

令 $z=\ln \frac{p}{1-p}$ 可得：

$p=\frac{1}{1+e^{-z}}={\omega }^{T}x+b$

即可以利用线性回归模型的预测结果去逼近事件真实的对数几率，因此，其对应的模型可以称为"对数几率回归" (logistic regression，中文常翻译成逻辑斯蒂回归)。可以利用极大似然估计法估计模型中的参数。

2 在sklearn包中的实现

scikit-learn 中 logistic 回归在 LogisticRegression 类中实现了二分类（binary）、一对多分类（one-vs-rest）及多项式 logistic 回归，并带有可选的 L1 和 L2 正则化。

class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100, multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)

几个主要的参数解释如下：
penalty：惩罚项，可选参数为 L1 和 L2，默认为 L2。L1 假设模型的参数满足拉普拉斯分布，L2 假设模型的参数满足高斯分布，其中 L2 对应的算法：‘newton-cg’、 ‘lbfgs’、 ‘liblinear’、 ‘sag’ ，L1 对应的算法只有 ‘liblinear’。
tol：停止求解的标准，float类型，默认为1e-4。
C：正则化系数λ的倒数，float类型，默认为1.0。
class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者 ’balanced’ 字符串，默认为不输入，也就是不考虑权重，即为 None。如果选择输入的话，可以选择 balanced 让类库自己计算类型权重，或者自己输入各个类型的权重，例如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。
solver：优化算法选择参数，即 newton-cg , lbfgs , liblinear , sag , saga ，默认为liblinear。liblinear 适用于小数据集，而 sag 和 saga 适用于大数据集因为速度更快。liblinear 支持 L1 和 L2，只支持 OvR 做多分类，“lbfgs”, “sag” “newton-cg”只支持L2，支持 OvR 和 MvM 做多分类。
a) liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
e) saga：线性收敛的随机优化算法的的变重。
multi_class：分类方式选择参数，可选参数为 ovr 和 multinomial，默认为 ovr。ovr 即前面提到的 one-vs-rest(OvR)，而 multinomial 即前面提到的 many-vs-many(MvM)。如果是二元逻辑回归，ovr 和 multinomial 并没有任何区别，区别主要在多元逻辑回归上。如果选择了 ovr ，则 liblinear，newton-cg , lbfgs，saga 和 sag 都可以选择；如果选择了 multinomial ，则只能选择 newton-cg , lbfgs sag 和 saga 。
OvR 的逻辑是：无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
MvM 则相对复杂，这里举 MvM 的特例 one-vs-one(OvO) 作讲解。如果模型有 T 类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为 T1 和 T2 的样本放在一起，把 T1 作为正例，T2 作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。

本文以 iris 数据集为例说明 LogisticRegression 如何调用：

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

# 抽取数据集与标签
X, Y = load_iris(return_X_y=True)
# 创建对象并实例化
#全部使用默认参数
clf = LogisticRegression() 
# 修改参数
#clf = LogisticRegression(random_state=0, solver='lbfgs',multi_class='multinomial')
clf.fit(X,Y)
# 利用创建的对象进行预测
clf.predict(X[:2, :])
# 显示预测的概率
clf.predict_proba(X[:2, :]) 
# 预测的准确率
clf.score(X, Y)

3 参考文献

1 周志华的机器学习
2 李航的统计学习方法
3 https://blog.csdn.net/jark_/article/details/78342644
4 https://blog.csdn.net/liulina603/article/details/78676723