详述——曼哈顿距离(L1度量)、欧式距离(L2度量)、切比雪夫距离(L∞度量)和编辑距离

最新推荐文章于 2025-03-24 15:19:17 发布

原创最新推荐文章于 2025-03-24 15:19:17 发布

· 1.7k 阅读

·

8

·

版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

最近在研究度量空间这一方向，总是混淆各种距离度量的定义，因此想记录一下自己对常用的四种距离度量的理解。

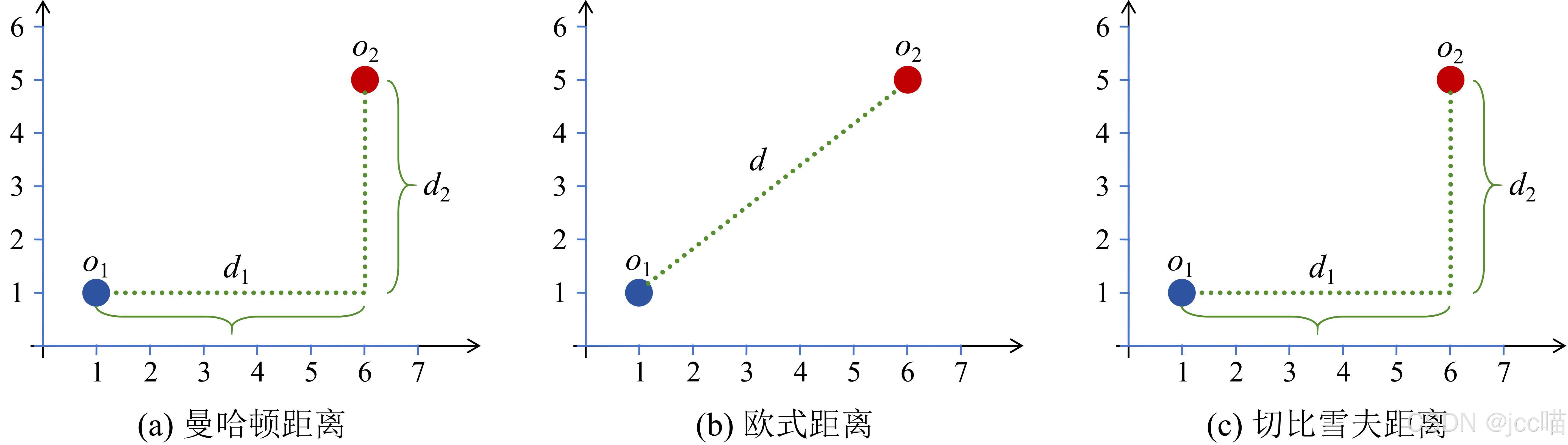
图1：三种Lp度量示例

1. 曼哈顿距离(L1度量)

（1）定义

曼哈顿距离是一种在几何度量空间中测量两点之间距离的方法，定义为在各坐标轴方向上距离的总和。在二维空间中，曼哈顿距离可以理解为从一个点到另一个点只能沿着水平或垂直方向行走的最小距离。

（2）公式

$dis(o_1,o_2) = \sum_{i=1}^{D}|o_1.i-o_2.i|$ 。

其中， $D$ 表示数据维度， $o_1.i, o_2.i$ 分别表示对象 $o_1, o_2$ 在第 $i$ 个维度上的值。

（3）举例

如图1(a)所示，在二维空间中(D=2)，对象 $o_1$ 到对象 $o_2$ 的距离为 $d_1+d_2=5+4=9$ 。

2. 欧式距离(L2度量)

（1）定义

欧式距离是指在欧几里得空间中两点间“普通”（即直线）的距离。

（2）公式

$dis(o_1,o_2) = \sqrt{\sum_{i=1}^{D}(o_1.i - o_2.i)^2}$ 。

其中， $D$ 表示数据维度， $o_1.i, o_2.i$ 分别表示对象 $o_1, o_2$ 在第 $i$ 个维度上的值。

（3）举例

如图1(b)所示，在二维空间中(D=2)，对象 $o_1$ 到对象 $o_2$ 的距离为

$\sqrt{(6-1)^2+(5-1)^2} = \sqrt{41}$ 。

3. 切比雪夫距离(L∞度量)

（1）定义

切比雪夫距离是指二个点之间各坐标数值差绝对值的最大值。（有点拗口）

（2）公式

$dis(o_1,o_2) = \max_{i=1}^{D}|o_1.i-o_2.i|$ 。

其中， $D$ 表示数据维度， $o_1.i, o_2.i$ 分别表示对象 $o_1, o_2$ 在第 $i$ 个维度上的值。

（3）举例

如图1(c)所示，在二维空间中(D=2)，对象 $o_1$ 到对象 $o_2$ 的距离为

$\max\{|6-1|,|5-1|\}=\max\{5,4\}=5$ 。

4. 编辑距离

（1）定义

编辑距离是指两个字串之间，由一个转换成另一个所需的最少编辑操作次数，允许的编辑操作包括：

将其中一个字符替换成另一个字符。
插入一个字符。
删除一个字符。

（2）公式：通常采用DP计算最小编辑距离，到时候单独写一个文章记录。

（3）举例

如图2所示，存在三个字串{"fame"，"game"，"acm"}。以计算"fame"与"acm"两个字串之间的距离为例，第一步删除"fame"的"m"字符，该字串变为"ame"；第二步在"ame"的"a"和"m"字符之间插入字符"c"，该字串变为"acme"；第三步删除"acme"的"e"字符，该字串变为"acm"；从字串"fame"转化为"acm"一共执行了三步操作，因此"fame"与"acm"之间的距离为3。

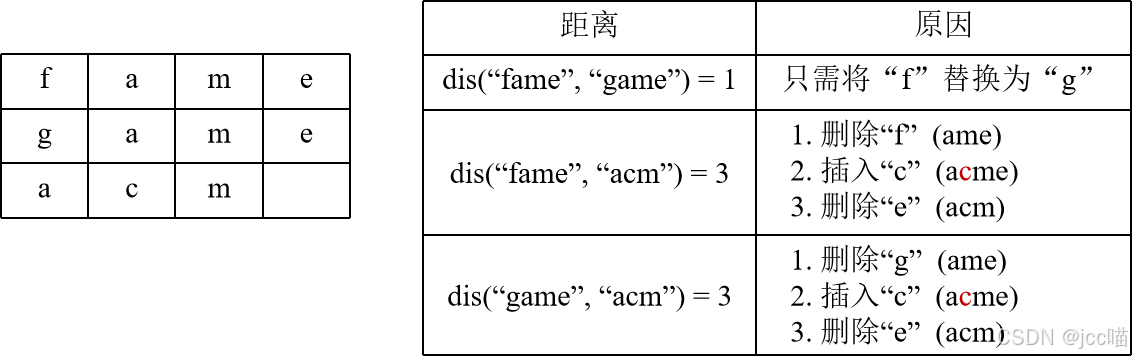图2：编辑距离计算示例

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。