💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
高强度聚焦超声模拟器中波束聚焦算法与热效应耦合机制的详细原理
💥1 概述
【高强度聚焦超声模拟器】模块是一种用于模拟分层介质中高强度聚焦超声波束和加热效应的工具。它由两个模块组成,分别是求解轴对称聚焦超声换能器压力分布的KZK方程模块和根据处理方案计算加热和热剂量的模块。
在第一个模块中,通过求解KZK方程,可以得到轴对称聚焦超声换能器在分层介质中的压力分布。这些计算结果被转储到Matlab工作区,并生成了相应的显著图。这些数据对于后续的处理非常有用。
第二个模块根据用户定义的处理方案,利用第一个模块得到的压力分布来计算加热和热剂量。通过考虑波束的衍射、干涉效应,以及吸收的幂律频率依赖性和相速度色散等因素,可以得到时间平均强度和加热速率。接着,将加热速率分布作为生物热传递(BHT)方程的源,通过积分来确定温度和热剂量场。这些结果可以用于进一步的研究和后处理。
为了保持软件的高效和轻量化,该模拟器对系统资源的要求较低,同时力求提供快速而准确的计算结果。它是研究高强度聚焦超声技术和其在生物医学领域中应用的有力工具。详细讲解见第4部分。详细文章见第4部分。
高强度聚焦超声模拟器中波束聚焦算法与热效应耦合机制的详细原理
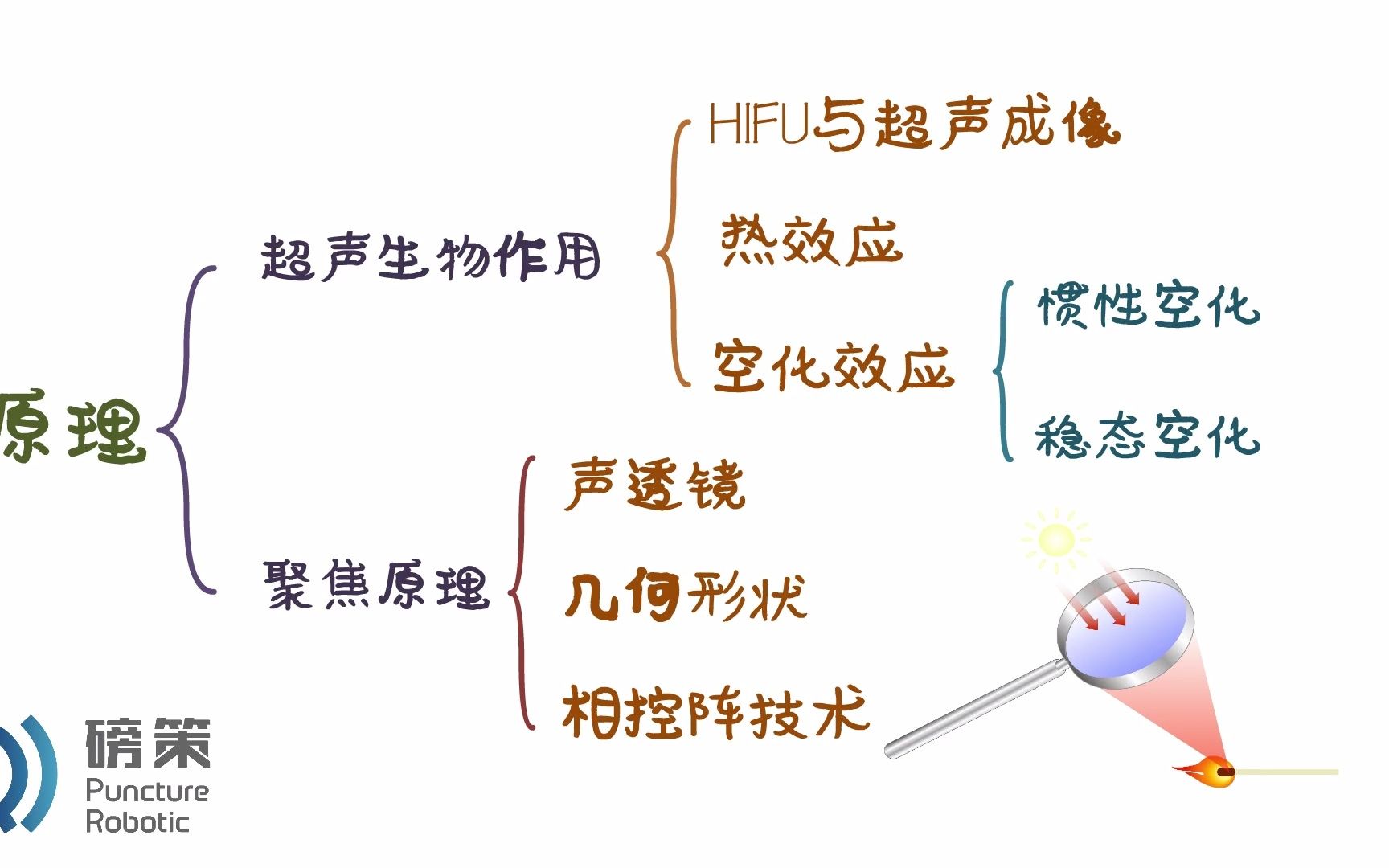
1. 波束聚焦算法核心原理
波束聚焦算法通过声场计算模块实现,主要基于非线性声学方程(如KZK方程或Westervelt方程)描述超声波在分层介质中的传播。例如,KZK方程综合考虑了衍射、非线性效应和吸收衰减,其离散化形式通过有限差分或谱方法求解。
- 声场建模:轴对称换能器的声压分布通过数值积分计算,考虑介质的分层特性(如声阻抗差异)对声波反射、透射的影响。
- 聚焦控制:通过时间延迟或相位调整实现动态聚焦,例如相控阵技术可动态调整焦点位置30。
HIFU 高强度聚焦超声的原理
代码片段示例:
[A1(k).IRK1, A1(k).IRK2] = KZK_operators(r, R, G1, dz, dr, J, k, gamma1(k));
2. 热效应耦合机制
热效应通过 生物热方程(BHTE) 与声场耦合,其核心公式为:

其中,Q为超声能量吸收产生的热源项,由声场强度分布决定。
- 热源计算:声场强度通过时间平均声压平方与吸收系数的乘积得到,吸收系数通常具有频率依赖性(如幂律模型)。
- 双向耦合:温度升高会改变介质的声速和密度,从而反作用于声场分布。例如,声速降低可能导致自聚焦效应,使焦点后移。
3. 数值实现方法
- 分步求解:先独立求解声场,再将声压分布作为热源输入BHTE。
- 并行加速:采用GPU加速有限元法或有限差分法,提升计算效率。
分层介质参数对模拟器的影响规律
1. 声学参数的影响
- 声速差异:不同层间的声速差异导致折射,影响焦点位置。例如,脂肪层(声速~1450 m/s)与肌肉层(~1580 m/s)的界面会引起焦点偏移。
- 声阻抗匹配:阻抗失配(如颅骨与软组织)导致反射损耗,需通过匹配层设计减少能量损失。
- 衰减系数:高频超声在衰减较高的介质(如骨骼)中能量迅速耗散,限制穿透深度。
2. 热学参数的影响
- 热导率:低热导率组织(如脂肪)易形成局部高温,但热量扩散慢可能损伤周围组织。
- 血流灌注率:高血流灌注区域(如肝脏)通过血流带走热量,降低热剂量累积。
- 非线性吸收:高频超声在组织中的吸收呈非线性增长,导致热沉积前移。
3. 参数敏感性分析
- 焦点位移敏感性:声速差异每增加5%,焦点位移可达2-3 mm。
- 温度分布依赖性:热导率变化±10%可使焦区最高温度波动±5°C。
现有文献中的多层组织模拟应用案例
1. 医疗领域应用
- 肿瘤治疗:模拟肝脏肿瘤的消融过程,考虑肝实质、血管和肿瘤组织的声学差异。例如,通过分层模型优化治疗参数,使焦区温度达65-85°C。
- 甲状旁腺消融:HIFU模拟器用于评估声波穿透颈部多层组织(皮肤、肌肉、腺体)的可行性。
2. 美容领域应用
- 超声炮技术:模拟HIFU在皮肤SMAS层的能量沉积,对比黄金超声炮与半岛超声炮的聚焦深度差异。
3. 教育与设备研发
- 教学培训:利用分层介质模型(如皮肤-脂肪-肌肉)演示声场分布与温度梯度。
- 颅骨穿透优化:设计声阻抗匹配层,减少颅骨对超声能量的反射。
4. 前沿研究案例
- 脑部治疗模拟:构建包含颅骨、脑脊液和脑实质的多层模型,预测HIFU焦点在深部脑区的准确性。
- 血管热损伤控制:模拟HIFU在肝脏血管附近的温度分布,避免血管壁过热破裂。
总结与展望
现有研究通过多物理场耦合模型(声-热-结构)实现了HIFU在分层介质中的高精度模拟。未来趋势包括实时反馈系统(如结合MRI温度监测)和多尺度建模(从细胞级损伤到器官级热分布)。需进一步探索病理组织参数数据库的构建,以提升个性化治疗的预测能力。
📚2 运行结果
这是一个模拟100瓦,1.5兆赫兹的高强度聚焦超声(HIFU)束在水中传播5厘米,然后在组织中传播3厘米到达聚焦点,然后继续传播8厘米的过程。在模拟运行时:运行结果如下:





function[z,r,H,I,Ppos,Pneg]=axisymmetricKZK()
% Driver for axisymmetric KZK integrator.
% get system parameters:
[p0,c1,c2,rho1,rho2,N1,N2,G1,G2,gamma1,gamma2,a,b,d,f,R,Z,z_,K] = KZK_parameters();
K2 = 2*K;
% print coefficients to screen:
fprintf('\n\tp0 = %2.2f MPa\n',1e-6*p0)
fprintf('\tN1 = %1.2f\tN2 = %1.2f\n',N1,N2)
fprintf('\tG1 = %3.2f\tG2 = %3.2f\n\n',G1,G2)
F=0.5*d/a;
if(F<1.37)
fprintf('\tWarning--f/%1.2f exceeds the conditions\n',F)
fprintf('\tunder which KZK is derived (> f/1.37).\n\n')
end
% grid set-up:
[M,J,J_,dz,dr,z,r]=computational_grid(Z,R,max(G1,G2),a,d,gamma2(1),N2);
% dependent variables:
u = zeros(2*J,K);
w = zeros(2*J,K);
limit = 1/sqrt(1-(a/d)^2);
v = initial_condition(J,K,G1,r,b*limit/a,limit);
v(1:J,1) = v(1:J,1).*sqrt(1-(r/d).^2);
v(J+1:2*J,1) = v(J+1:2*J,1).*sqrt(1-(r/d).^2);
% set up discretization operators:
for k=1:K
[A1(k).IRK1,A1(k).IRK2,A1(k).CN1,A1(k).CN2] ...
= KZK_operators(r,R,G1,dz,dr,J,k,gamma1(k));
[A2(k).IRK1,A2(k).IRK2,A2(k).CN1,A2(k).CN2] ...
= KZK_operators(r,R,G2,dz,dr,J,k,gamma2(k));
end
k1 = zeros(2*J,1); % IRK slope vectors
k2 = zeros(2*J,1);
b1 = 1/sqrt(2); % IRK coefficients
b2 = 1 - b1;
% parameters for nonlinear integration:
mu1 = N1*K*dz/pi; % nonlinear term integration parameters
mu2 = N2*K*dz/pi;
cutoff1 = gamma1(1)/10/N1; % cutoffs for performing nonlinear integration
cutoff2 = gamma2(1)/10/N2;
X = zeros(1,K2); % data vectors
Y = zeros(1,K2);
Xpeak = zeros(1,K2);
% for plotting routines:
H = zeros(J_,M); % Heating rate matrix
H2 = zeros(J_,M);
H(:,1) = real(gamma1(1))*(v(1:J_,1).^2 + v(J+1:J+J_,1).^2);
I = zeros(J_,M);
I(:,1) = v(1:J_,1).^2 + v(J+1:J+J_,1).^2;function[z,r,H,I,Ppos,Pneg]=axisymmetricKZK()
% Driver for axisymmetric KZK integrator.
% get system parameters:
[p0,c1,c2,rho1,rho2,N1,N2,G1,G2,gamma1,gamma2,a,b,d,f,R,Z,z_,K] = KZK_parameters();
K2 = 2*K;
% print coefficients to screen:
fprintf('\n\tp0 = %2.2f MPa\n',1e-6*p0)
fprintf('\tN1 = %1.2f\tN2 = %1.2f\n',N1,N2)
fprintf('\tG1 = %3.2f\tG2 = %3.2f\n\n',G1,G2)
F=0.5*d/a;
if(F<1.37)
fprintf('\tWarning--f/%1.2f exceeds the conditions\n',F)
fprintf('\tunder which KZK is derived (> f/1.37).\n\n')
end
% grid set-up:
[M,J,J_,dz,dr,z,r]=computational_grid(Z,R,max(G1,G2),a,d,gamma2(1),N2);
% dependent variables:
u = zeros(2*J,K);
w = zeros(2*J,K);
limit = 1/sqrt(1-(a/d)^2);
v = initial_condition(J,K,G1,r,b*limit/a,limit);
v(1:J,1) = v(1:J,1).*sqrt(1-(r/d).^2);
v(J+1:2*J,1) = v(J+1:2*J,1).*sqrt(1-(r/d).^2);
% set up discretization operators:
for k=1:K
[A1(k).IRK1,A1(k).IRK2,A1(k).CN1,A1(k).CN2] ...
= KZK_operators(r,R,G1,dz,dr,J,k,gamma1(k));
[A2(k).IRK1,A2(k).IRK2,A2(k).CN1,A2(k).CN2] ...
= KZK_operators(r,R,G2,dz,dr,J,k,gamma2(k));
end
k1 = zeros(2*J,1); % IRK slope vectors
k2 = zeros(2*J,1);
b1 = 1/sqrt(2); % IRK coefficients
b2 = 1 - b1;
% parameters for nonlinear integration:
mu1 = N1*K*dz/pi; % nonlinear term integration parameters
mu2 = N2*K*dz/pi;
cutoff1 = gamma1(1)/10/N1; % cutoffs for performing nonlinear integration
cutoff2 = gamma2(1)/10/N2;
X = zeros(1,K2); % data vectors
Y = zeros(1,K2);
Xpeak = zeros(1,K2);
% for plotting routines:
H = zeros(J_,M); % Heating rate matrix
H2 = zeros(J_,M);
H(:,1) = real(gamma1(1))*(v(1:J_,1).^2 + v(J+1:J+J_,1).^2);
I = zeros(J_,M);
I(:,1) = v(1:J_,1).^2 + v(J+1:J+J_,1).^2;
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
























 1564
1564

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








