一道复杂积分求解（被积函数为三角函数与分式的复合函数）

天街雨佳

于 2024-09-14 14:47:22 发布

阅读量558

点赞数 9

文章标签：笔记

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/x22116448341/article/details/142256678

版权

积分运算是微积分中是非常常见的一类问题，然而有些积分的运算方法非常巧妙，对于大多数人而言，想出相应的正确求解思路并不是一件容易的事情。下面这个积分就是一个典型的例子：

$\int_{0}^{\pi}\frac{sin^2x}{9-cos^2x}dx$

不难分析， $9-cos^2 x>0$ 对于任意实数 $x$ 均成立，因而被积函数没有奇点，此积分必然收敛。被积函数的分子是 $sin^2x$ ，直接换元确实非常困难；为了求解这道积分，核心知识点主要是两个恒等式，分别为 $csc^2x=\frac{1}{sin^2x}=-\frac{ dcot(x)}{dx}$ 和 $csc^2x=cot^2x+1$ ，最核心的求解步骤则是对被积函数的分子和分母同时乘以 $csc^4x$ .下面则是标准的求解过程：

对原积分的分子和分母同时乘以 $csc^4x$ ,可得：

$\int_{0}^{\pi}\frac{csc^2x}{9csc^4x-cot^2xcsc^2x}dx=\int_{0}^{\pi}-\frac{-csc^2x dx}{9(cot^2x+1)^2-cot^2x(cot^2x+1)}$

令 $cot x=u$ ,则 $du=-csc^2x dx$ ,原积分进一步可以转化为

$\int_{-\infty}^{+\infty}\frac{du}{(u^2+1)(8u^2+9)}=\int_{-\infty}^{+\infty}\frac{(u^2+\frac{9}{8})-(u^2+1)}{(u^2+1)(u^2+\frac{9}{8})}du$

$=\int_{-\infty}^{+\infty}\frac{1}{u^2+1}-\frac{1}{u^2+\frac{9}{8}}du$

$=\pi-\int_{-\infty}^{+\infty}\frac{du}{u^2+\frac{9}{8}}$

$=\pi-\frac{8}{9}\int_{-\infty}^{+\infty}\frac{du}{(\frac{2\sqrt{2}}{3}u)^2+1}$

令 $v=\frac{2\sqrt{2}}{3}u$ ,则原积分可进一步化简为

$\pi-\frac{2\sqrt{2}}{3}\int_{-\infty}^{+\infty}\frac{dv}{v^2+1}=(1-\frac{2\sqrt{2}}{3})\pi$

为了验证自己算得对不对，可以在网址https://www.wolframalpha.com/上输入命令

int sin^2x/(9-cos^2x), from 0 to pi

发现最终可以得到和先前运算一致的结果：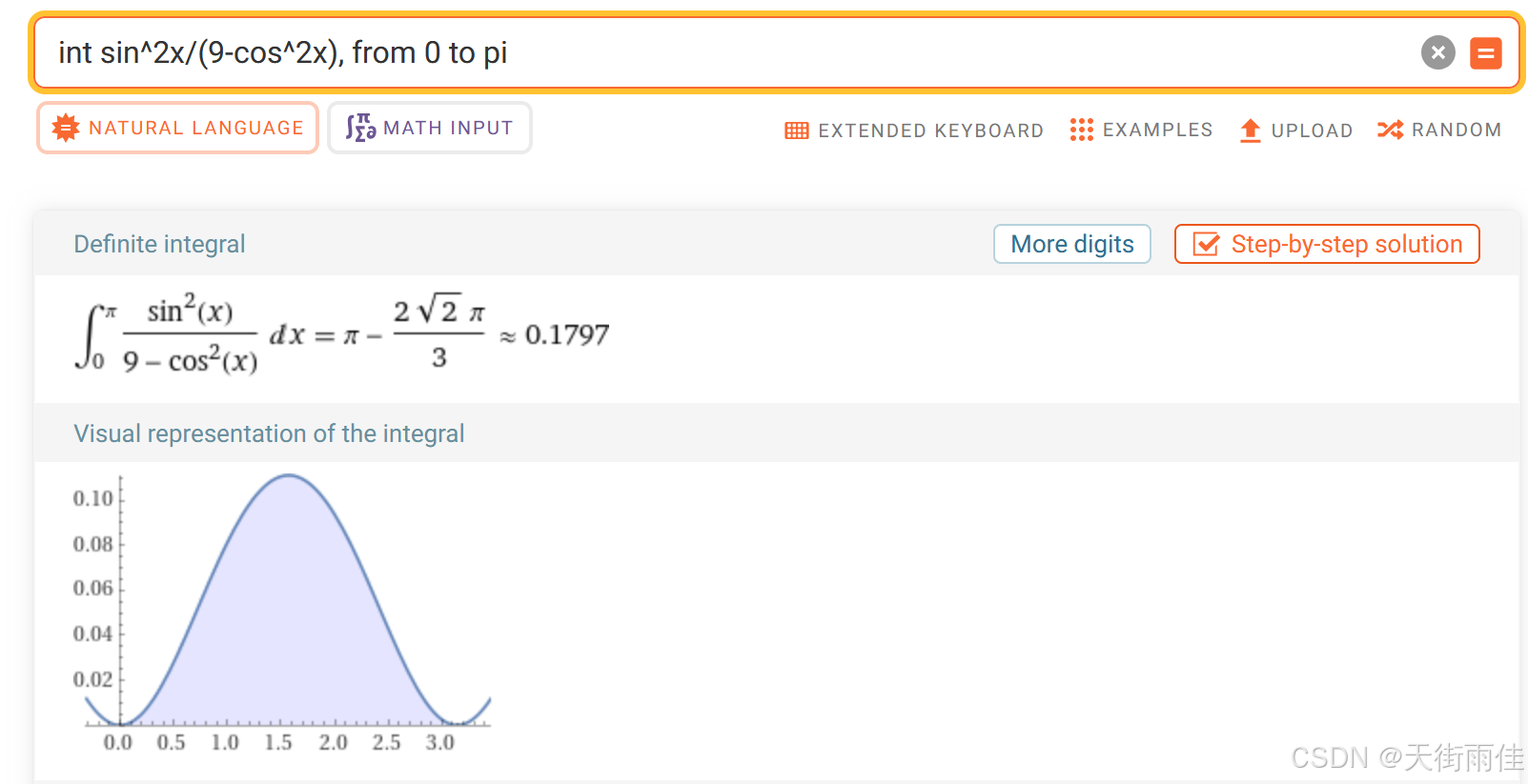

此结果进一步验证了运算过程的正确性，不得不说，这道积分的求解思路过于精妙，因而平时的积累是学习中非常关键的一环！

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。