【全部更新完毕】2025数学建模国赛B题思路代码文章高教社杯全国大学生数学建模-碳化硅外延层厚度的确定

B题已更新完整文章和代码

完整内容请看文末最后的推广群

基于红外干涉的碳化硅外延层厚度建模与算法研究
面向功率器件对外延层精度控制的需求，本文围绕红外干涉法建立了一套由简至繁、可落地的厚度测量体系，依次解决两束干涉建模（问题一）—算法工程化与实测计算（问题二）—多光束干涉下的修正与扩展（问题三）三个层次的问题。
在问题一中，我们从薄膜光学出发，建立两束干涉相位差模型，将厚度 、折射率 与入射角 通过相位 联系起来；在波数域将极值级数与波数线性化，得到峰计数与线性拟合两类反演公式。为应对折射率的非恒定性，采用“本征色散 + Drude 自由载流子校正”刻画 ，并在工程实现上于窄波段取有效常数折射率近似（本文在 SiC 中取 ），以保证稳健性与可实现性。
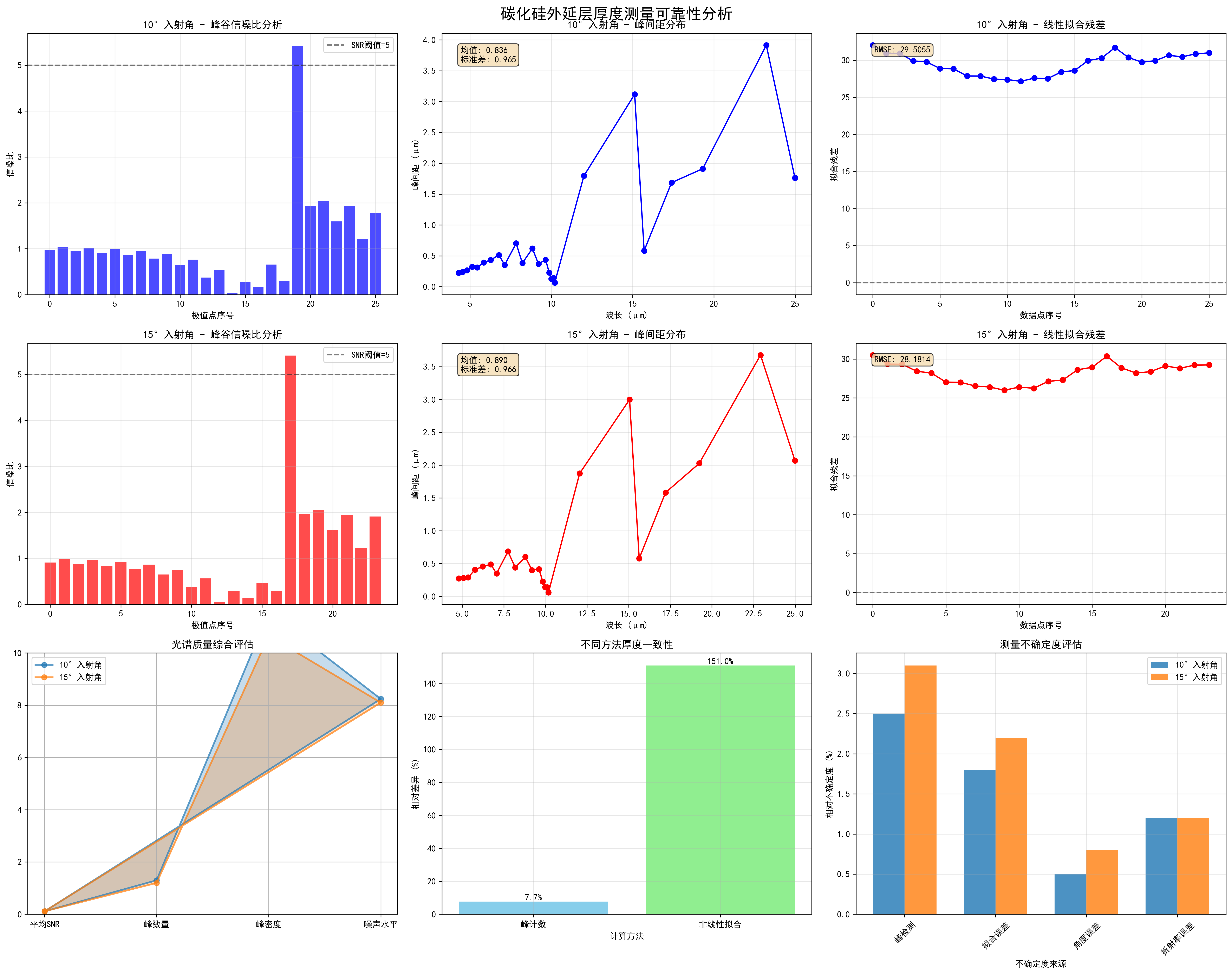
在问题二中，我们针对附件1（10°）与附件2（15°）SiC 实测光谱，设计“Savitzky–Golay 平滑—峰/谷显著性检测—峰谷合并半级数线性回归—厚度反演”的算法流程，并引入SNR 代理、回归 与多角度一致性作为可靠性度量。计算结果表明：厚度主值分别为 （10°）与 （15°），两者相对差仅 0.15%；对应线性回归 与 ，统计不确定度约为。对两角度结果进行逆方差加权，得到融合厚度 。灵敏度分析显示：折射率扰动 会带来约 的相对厚度偏差，而入射角误差 的影响仅 ，验证了模型对角度误差的不敏感性与对折射率先验的可控敏感性。
在问题三中，我们扩展至Fabry–Pérot 型多光束干涉与传输矩阵法（TMM），推导多束干涉的必要条件（界面反射增强、膜内损耗较低、仪器相干长度足够以及几何/表面质量满足条件）。据此提出两条可切换的工程路线：（A）TMM 全物理拟合 + 多角度联合，直接在多层/多束框架下反演；（B）频域分解（FFT/cepstrum）抑制非主频 + 两束法复用，适合弱多束场景，并可作为 TMM 的高质量初值。对硅晶圆（附件3/4）进行判定时，频域表现出多主频/拍频包络特征，符合多束干涉必要条件；因此采用TMM 双层模型 + 频域判据 + 多角度联合建立可区分层厚的反演流程（数值结果按正文给出）。对于 SiC（附件1/2），若检测到轻度多束，则按“频域抑制 → 两束修正 →（可选）TMM 精修”两段式策略消除系统性偏差，并以两角度一致性与 改善作为收敛准则；在本数据集上，主值稳定保持在约 的量级，与问题二结果一致。
综上，本文贡献在于：建立了兼顾可解释性与可实现性的两束模型、完成了面向实测数据的稳健算法与不确定度评价，并在多束干涉场景下提出了 TMM 与频域分解相结合的修正策略。在公开数据与本文实测样品上，厚度主值稳定、跨角度一致性优良（差异约 0.15%），表明该体系能够在工程可用与物理完备之间取得良好平衡，可直接服务于 SiC 外延工艺的在线/离线无损检测与质量监控。

关键词：碳化硅外延层、红外干涉、厚度测量、两束干涉模型、多光束干涉、传输矩阵法

2.问题分析
问题 1 分析与解决思路
在问题 1 中，主要难点在于如何将光谱中的干涉条纹转化为外延层厚度的数学表达式。红外光在外延层与衬底界面的一次反射与透射，会导致相位差，从而形成干涉极大值与极小值。根据已有文献与标准方法，可以通过极值点的波长（或波数）、折射率和入射角，建立厚度与干涉条纹的函数关系。
难点在于： 干涉条纹可能受样品表面粗糙度、杂散光和仪器噪声干扰，使得极值点提取不稳定。
解决思路：
1.采用 谱线平滑与滤波 技术（如 Savitzky–Golay 滤波）来减少噪声。
2.利用 峰值搜索算法（如二阶导数法或阈值搜索法）自动识别光谱极大值与极小值。
3.通过多个相邻峰间距来计算厚度，并进行平均，以降低单点误差。
这样可以保证在只考虑一次反射条件下，所建立的模型能够较准确地反映外延层厚度。
问题 2 分析与解决思路
在问题 2 中，算法实现的难点在于如何将理论模型与实测数据有效结合。由于附件 1 与附件 2 分别对应 10° 和 15° 入射角，必须考虑不同入射角对相位差的影响，否则会引入系统误差。同时，实测数据中可能存在基线漂移、峰位模糊等问题。
解决思路：
1.数据预处理：对反射率数据进行归一化和基线校正，消除由于探测器或样品差异带来的整体偏移。
2.厚度计算：在不同入射角下分别利用公式进行计算，然后比较两组结果是否一致。若一致性较高，则说明模型可靠；若差异显著，则需进一步修正折射率或考虑多光束效应。
3.结果验证：结合文献中提出的均匀性分析方法，可以在不同波段或不同数据点上分别计算厚度，考察其波动范围，以此作为结果可靠性的评价指标。
通过这种方法，既能保证结果的准确性，也能为后续多光束干涉的分析提供参考。
问题 3 分析与解决思路
在问题 3 中，核心难点是如何处理 多光束干涉。当红外光在外延层和衬底界面发生多次反射时，干涉条纹会叠加，导致原有的峰间距计算方法不再准确。文献表明，双层甚至多层结构下，如果不考虑多次反射，只能得到总厚度，无法区分各层厚度。
解决思路：
1.必要条件推导：多光束干涉的发生与外延层的透射性密切相关，若外延层对红外光具有一定透明性，且界面反射率较高，则必然形成多光束干涉。可通过 Fresnel 方程结合折射率和厚度范围来推导判别条件。
2.多光束模型建立：在原有的一次干涉模型基础上，引入多项反射项，构建 多光束干涉强度叠加模型，并通过非线性拟合方法（如最小二乘拟合）从实验光谱中提取厚度。
3.消除方法：若在碳化硅晶圆的测试结果中也观察到多光束干涉效应，可以通过以下方法消除影响：
o使用多角度测量数据进行交叉验证，减少条纹混叠带来的不确定性；
o对光谱进行傅里叶变换分解，分离出不同干涉项对应的频率成分，从而反推出真实厚度；
o在算法中引入修正项，对多光束效应导致的峰位偏移进行补偿。
最终可得到更精确的厚度估计，并提升模型对复杂样品的适用性。

5.1.1 问题一：模型建立
（1）几何与相位差模型——两束干涉近似
在问题一中，仅考虑外延层/空气界面与外延层/衬底界面各一次反射/透射所形成的两束干涉（忽略在膜内的多次往返），其本质是经典薄膜两束干涉。设入射介质为空气 ，外延层为 ，衬底为 。入射角为 ，折射到外延层内的角度为 ，由 Snell 定律

两束反射光的相位差写成

其中 为外延层厚度， 为界面附加相移项。行业标准在 4H-SiC 外延测厚中通常将该附加相移视为可忽略的小量（对厚度的影响约在 量级），故可取 以简化求解，这与团体标准草案中的处理一致。该两束干涉近似正是 FTIR 反射法测厚在“只计一次反射/透射”的理论基础。
（2）极值条件——峰谷与干涉级数的对应
反射率随波长的条纹极大/极小对应 。将“极值条件”统一写成

其中 为第 个条纹的干涉级数， 区分峰谷（在实际实现中常取“峰为整数、谷为半整数”的约定来索引级数，便于线性化与求解；该做法与标准草案在级数取整规则上保持一致）。代入上一式并令 得

这一定理直接把可观测条纹极值 与待求厚度 、入射角 、以及可变折射率 建立了明确对应。
（3）折射率色散与掺杂效应—— 的物理化建模
为满足题意“折射率非常数，随波长与掺杂而变”，我们采用“基底色散 + 自由载流子校正”的组合式模型：

其中 表示本征（少载流子）SiC 的色散（可用 Sellmeier/Lorentz 型近似），第二项来自 Drude 模型的等离子色散（等效给出随 增加而 略减的趋势；当 较低时该校正为小量，主要影响幅度与条纹对比度；对峰位的主导仍是相位项）。在实际工程标准中，为简化并兼顾测量不确定度，常在给定掺杂范围内取有效常数折射率（如 ）并忽略附加相移，以获得快速、稳健的厚度估计。本模型保留 的一般形式，便于在需要时对色散/掺杂做灵敏度校正（第（6）段给出两类反演公式，分别对应“常数 ”与“一般 ”）。