前面我们已经介绍过矩阵的两个重要空间:列空间和零空间,今天继续介绍矩阵的另外两个重要空间:行空间和左零空间。A的行空间就是AT的列空间,A的左零空间就是AT的零空间,文字描述起来比较拗口,用数学符号表示一下就会简单明了:对于矩阵A,其列空间是C(A),零空间N(A),行空间是C(AT),左零空间是N(AT)。注意,虽然今天新增的这两个空间涉及AT ,但我们还是从A的角度去看待这两个子空间。
4个子空间的维数分别是多少?
A为m*n矩阵,秩为r,A的零空间N(A)里都是n维向量,所以N(A)是Rn的子空间,列空间C(A)是所有列的线性组合,每列是m维,所以C(A)是Rm的子空间,同样行空间C(AT)是Rn的子空间,而左零空间N(AT)是Rm的子空间,首先结合以前的知识,我们知道列空间C(A)的维数是r,零空间N(A)维数是n-r,行空间C(AT)维数是r(A转置的主元数与A的主元数是相同的),左零空间N(AT)是m-r。
4个子空间的基分别是什么?
对于列空间,我们已经学会使用消元确定主元列,而主元列就是C(A)的一组基,对于零空间,我们也可以学会利用行最简式去寻找基,即特殊解,那么对于行空间和左零空间,我们当然也可以将矩阵A转置后再采用相同的方法去求,但直觉告诉我们求行空间的基、左零空间的基应该有更便捷的方法,那我们就可以减少工作量了。
我们在求列空间时,会对矩阵A进行消元并化简,如下所示,最终将A化到行最简式R,
很明显R的列空间不等于A的列空间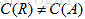
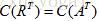
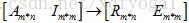 ,其中R是A的行最简形,从上面的过程可以看出,对A进行了什么样的操作,就对I进行了什么样的操作,所以E记录了所有的行变换,且E*A=R,对于刚刚的的例子,我们可求出E=
,其中R是A的行最简形,从上面的过程可以看出,对A进行了什么样的操作,就对I进行了什么样的操作,所以E记录了所有的行变换,且E*A=R,对于刚刚的的例子,我们可求出E=
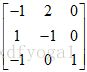 ,因为R中的第3行是0
T,又因为E*A=R,因此我们就找到了这样的y
T,所以E的第3行就是A的行空间的基,从E中我们不仅可以得到左零空间的维数,还能求出整个左零空间,对于上面这个例子,左零空间的维数是1,基只有一个向量。以上就是求左零空间基的方法,其实求消元矩阵E也不是一件容易的事,但是至少我们不需要把矩阵转置然后从头开始计算。
,因为R中的第3行是0
T,又因为E*A=R,因此我们就找到了这样的y
T,所以E的第3行就是A的行空间的基,从E中我们不仅可以得到左零空间的维数,还能求出整个左零空间,对于上面这个例子,左零空间的维数是1,基只有一个向量。以上就是求左零空间基的方法,其实求消元矩阵E也不是一件容易的事,但是至少我们不需要把矩阵转置然后从头开始计算。








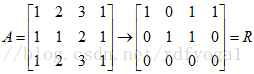














 2923
2923











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








