线性变换及其对应的矩阵

变换有很多种形式，它描述了输入和输出间的映射（mapping/map）关系，这篇文章主要讨论线性变换，每个线性变换都对应一个矩阵，线性变换与坐标无关，而矩阵与坐标有关，因此矩阵是基于坐标来描述线性变换，例如投影就是一种常见的线性变换，与其对应的是投影矩阵，判断是线性变换需满足以下两个条件：

其中v和w分别是向量，T表示对向量的变换，上两式表明线性变换应该保证加法和乘法的不变性，这两个条件可合并为一个条件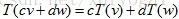： ，前面提及的投影变换，满足一个向量乘以倍数，其投影也乘以相应倍数，两向量和的投影等于各自投影的和，再举几个例子，用上面的两个条件来判断其是否为线性变换。

例1：向量平移。假设向量v沿着某方向平移v0，即T(v)=v+v0，很明显这不是线性变换，因为如果向量v的长度加倍，T(v)并不会加倍。除了用上面的两个条件来判断之外，还可以通过T(0)来判断是否为线性变换，线性变换必须满足零向量经过变换后一定等于零向量，从这一点也可看出例1不是线性变换。

例2：平方运算。例如求向量的长度，T(v)=||v||，如果向量乘以-2，则其长度还是变为原来的2倍，而不是乘以-2，因此平方运算是一种非线性变换。

例3：旋转变换。假设输入向量为v，将其旋转45度后得到输出向量T(v)，如果加倍v，则输出向量也加倍，对于v+w，其旋转的结果等于v和w各自旋转的结果相加，因此旋转也是一种线性变换。

由于每一个线性变换都对应了一个矩阵，因此线性变换的过程可以表示为T(v)=Av，其中A是变换矩阵，x是输入向量，理解线性变换的方法就是确定其背后的矩阵A，因为线性变换的本质都包含在矩阵中。例如有一线性变换T，其输入是3维向量，输出是2维向量，即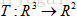 ，则该变换对应的A应该是一个2*3矩阵。

我们现已理解单个向量线性变换的结果，例如T(v₁)，但如果要考虑线性变换对于整个输入空间造成的影响呢？难道要对输入空间中的向量一个个进行计算吗？答案很明显不是，只要确定了线性变换对于该空间基向量的影响，就能了解线性变换对于整个输入空间的影响，也就是说只要确定了 T(v₁) T(v₂) …T(v_n)，其中v₁…v_n是输入空间的一组基，简称输入基，就足以确定任何v的线性变换T(v)，因为v总是基向量的线性组合v=c