振动信号幅值成分分析手段

liulangzhehwm

已于 2024-12-11 10:26:14 修改

阅读量1.5k

点赞数 8

分类专栏：轴承故障诊断的基本知识和信号分析文章标签：笔记

于 2024-04-18 10:30:40 首次发布

本文链接：https://blog.csdn.net/xiaiming0/article/details/137904569

版权

轴承故障诊断的基本知识和信号分析专栏收录该内容

9 篇文章

订阅专栏

提示：振动信号幅值成分分析手段

文章目录

一、有量纲特征分析
二、概率密度分析
三、无量纲分析
四、总结（自己的思想）

提示：以下是本篇文章正文内容，下面案例可供参考

一、有量纲特征分析

在这里插入图片描述

均值和平均幅值可以用于描述信号中的直流分量，反映能量波动的情况。
方根幅值和均方根体现了所包含能量的多少。
最大值、最小值和峰值可以用于观察振动信号强度的变化，它们与瞬时脉冲呈正相关，故障脉冲越大，相应的值也会越大。
标准差体现了偏移中心的变化。

在运行过程中，随着故障的产生和发展，有量纲指标的参数值也会不断变化。

平均幅值：是对原始信号时域幅值求绝对值然后再求和。
方根幅值：是对原始信号时域幅值求绝对值再开根号然后在求和，根据根号的特点可以放大幅值较小的值，可以缩小幅值较大的值（如果是开4次甚至是6次方根呢？）。
均方根：是对原始信号时域幅值求平方然后再求和，根据平方的特点可以放大幅值较大的值，可以缩小幅值较小的值（如果是开4次（峭度）甚至是6次方呢？）。

这些特征是有量纲的特征，有量纲特征会因负载、转速等外界因素产生改变，所以根据值来做故障诊断就很可爱了。
如果跟踪这三个值，可以初步分析原始信号时域幅值的成分的变化。

二、概率密度分析

2.1、原理

概率密度函数给出了信号取不同幅值大小的概率，在随机振动、随机疲劳试验等应用场合，常常利用它来检测信号的正态性和了解信号的幅值大小分布情况。
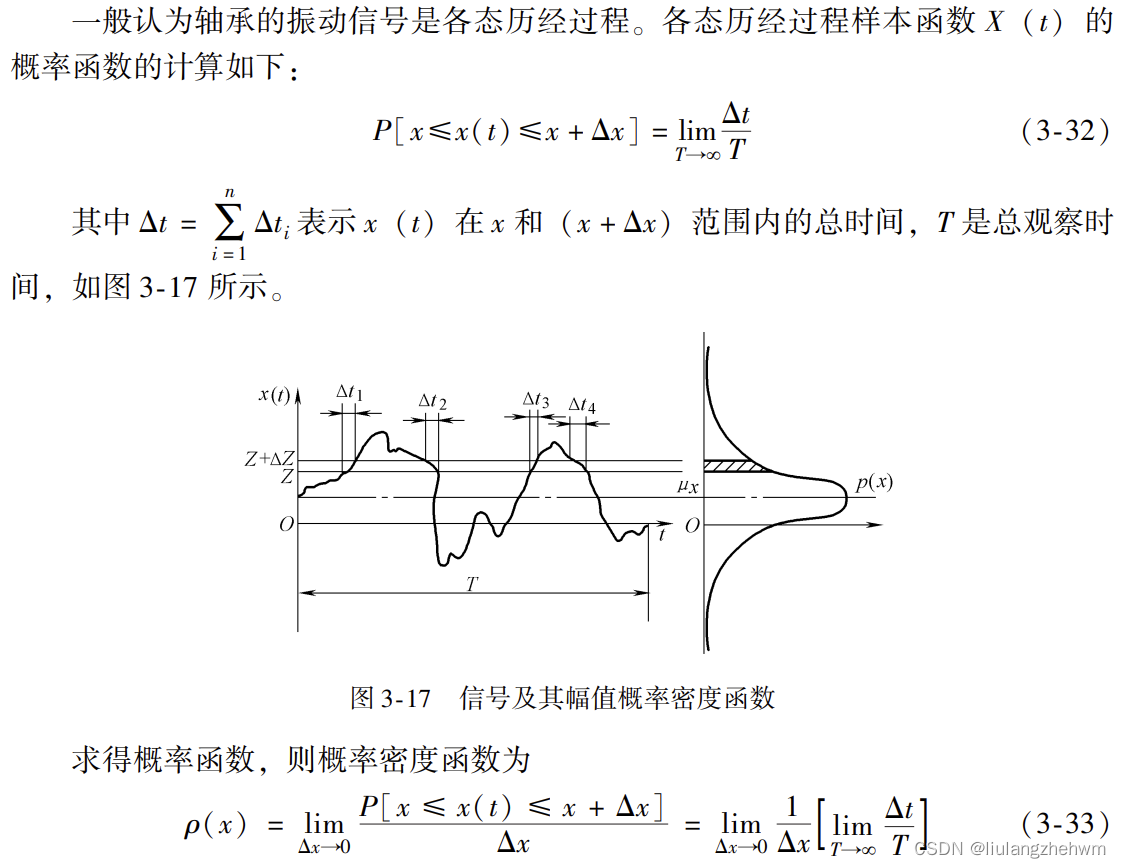
在这里插入图片描述
经过大量的实践证明，多数情况下，正常滚动轴承的振动信号是各态历经过程，且其幅值的概率分布为高斯分布（正态分布）。但轴承在运行过程中，如果出现点蚀、剥落、划伤等局部损伤类故障时就会引起冲击，其振动信号幅值的概率密度会偏离正态分布，从得出的轴承振动幅值概率分布直方图中能够大概看出轴承是否已经出现了故障（故障检测）。

2.2、代码

# 绘制概率密度图
plt.figure(figsize=(8, 5))
# i:故障信号，画成条形图
hist, bins = np.histogram(i, bins=100, density=True)
plt.bar(bins[:-1], hist, edgecolor="white", zorder=1, width=bins[1] - bins[0])
# j:和故障信号同工况的健康信号，化成折线图
hist, bins = np.histogram(j, bins=100, density=True)
plt.plot(bins[:-1], hist,color="y")

plt.title("故障说明")
plt.savefig(".\\picture\\crwu1\\" + str(i_index) + "-" + mapdata_all1[i_index] + ".png")
# 显示图表
plt.show()

2.3、结果分析

在这里插入图片描述

可以看到在发生故障时，幅值高的成分变多（注意上图的横坐标代表的是信号的幅值，纵坐标表示的是发生的次数）。

三、无量纲分析

在这里插入图片描述

根据幅值概率密度分布函数可得出几种典型信号的时间波形和对应的概率密度函数的关系如上图所示。图中(a)为正弦波信号，可知正弦信号的概率密度函数P(x)曲线呈盆形;（c)为正弦波加随机信号，概率密度函数P(x)曲线是正弦波和随机噪声叠加形成的“M”形;(b)为随机噪声信号, 随机噪声信号的概率密度函数P(x)通常为或近似为正态曲线。比较这几个典型信号的概率密度函数曲线差异可以得出以下结论:

不同信号的幅值概率密度函数曲线也不同，这就是利用概率密度函数P(x)曲线进行故障诊断的理论依据。若某种振动信号的幅值概率密度函数曲线呈正态分布或接近正态分布则说明其振动以随机噪声形式出现;呈盆形或者“M”形时表明振动信号中大幅值概率很高是出现故障的重要信息。至于故障类型则要根据诊断对象的实际结构进行故障机理分析也可结合其它故障诊断方法确诊。

在这里插入图片描述

四、总结（自己的思想）

要用变化的思想去做信号分析
要用对比的思想去做信号分析
故障信号和正常不一样，这个不一样可以是幅值较高的成分所占的比例，这个是绝对的。
故障信号之所以是故障信号不是因为故障信号的最大值多大，而是最大值发生了突变。
峭度指标对早期的故障敏感，但是稳定性不好；有效值虽然对故障敏感度不高，但是稳定性很好，且随着故障发展是单调上升的，因此两者可以结合分析。

有量纲幅域诊断参数如方根幅值、平均幅值、歪度和峭度等的数值虽然会随着故障的发展而上升但也会因工作条件(如负载、转速、仪器灵敏度等)的改变而变化，实际上难以区分。这是有量纲幅域诊断参数的不足。所谓无量纲指标(Non- dimensional Paralneter)是由两个具有相同量纲的量的比值组成，当它描述某一特定体系时具有一定的物理意义。无量纲诊断是一种将“无量纲参数”用于设备故障诊断的技术方法，无量纲幅域诊断参数如波形指标、峰值指标.脉冲指标、峭度指标等对故障足够敏感而对信号的幅值和频率的变化不敏感，即和机器的工作条件关系不大。这些性质是非常重要和有用的。