【更新】请看我的另一篇博客
https://blog.csdn.net/xiaojiajia007/article/details/75041651
[重点]转置卷积的解释,避免三个误区: 点击打开链接
Y = CX 卷积操作矩阵C定义排列如下:
很多文章都说卷积核的转置就可以求反卷积,又陷入迷茫“就算把卷积核转置(或者左右翻转上下翻转),卷积后输出还是越来越小(或不变,至少不会增大)啊”……直到看到文献和相应的这个动画(其他动画在github-convolution arithmetic1)
 |  |
|---|---|
| 卷积 i=4,k=3,p=0,s=1,则 o=2 | 反卷积 i=2,k=3,p=0,s=1,则 o=4 |
注意图中蓝色(下面)是输入,绿色(上面)是输出,卷积和反卷积在 p、s、k 等参数一样时,是相当于 i 和 o 调了个位。
这里说明了反卷积的时候,是有补0的,即使人家管这叫 no padding( p=0)), ,这是因为卷积的时候从蓝色 4×4 缩小为绿色 2×2, 所以对应的 p=0 反卷积应该从蓝色 2×2 扩展成绿色 4×4。而且转置并不是指这个 3×3 的核 w 变为 wT,而是值卷积操作矩阵C的转置。但如果将卷积计算写成矩阵乘法(在程序中,为了提高卷积操作的效率,就可以这么干,比如tensorflow中就是这种实现), Y⃗ =CX⃗ (其中 Y⃗ 表示将 Y⃗ 拉成一维向量, X⃗ 同理),那么反卷积确实可以表示为 CTY⃗ ,而这样的矩阵乘法,恰恰等于 w 左右翻转再上下翻转后与补0的 Y 卷积的情况。具体看链接博客
全文: Convolution Arithmetic Tutorial 点击打开链接
github上关于卷积与转置卷积的动态图 点击打开链接
结论:
Quick reference
Convolution relationship
A convolution specified by
- input size
 ,
, - kernel size
 ,
, - stride
 ,
, - padding size
 ,
,
has an output size given by

In Theano, this translates to
output = theano.tensor.nnet.conv2d(
input, filters, input_shape=(b, c2, i1, i2), filter_shape=(c1, c2, k1, k2),
border_mode=(p1, p2), subsample=(s1, s2))
# output.shape[2] == (i1 + 2 * p1 - k1) // s1 + 1
# output.shape[3] == (i2 + 2 * p2 - k2) // s2 + 1
Transposed convolution relationship
A transposed convolution specified by
- input size
 ,
, - kernel size
 ,
, - stride
 ,
, - padding size
 ,
,
has an output size given by

where  is a user-specified quantity used to distinguish between the
is a user-specified quantity used to distinguish between the different possible output sizes.
different possible output sizes.
Unless  , Theano requires that
, Theano requires that is implicitly passedvia an
is implicitly passedvia aninput_shape argument. For instance, if ,
, ,
, ,
, and
and , then
, then and the Theano code would look like
and the Theano code would look like
input = theano.tensor.nnet.abstract_conv.conv2d_grad_wrt_inputs(
output, filters, input_shape=(9, 9), filter_shape=(c1, c2, 4, 4),
border_mode='valid', subsample=(2, 2))








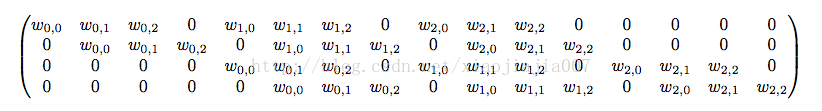















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








