机器人理论
介绍
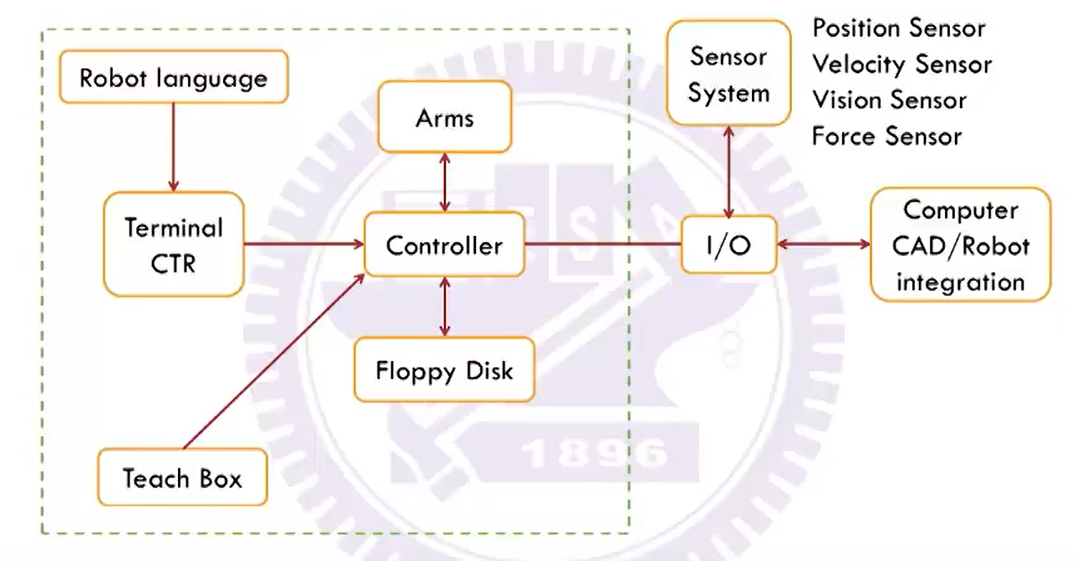
结构:
空间变换
坐标系变换
位置平移 A P B _ o r i g i n ^AP_{B\_origin} APB_origin & 位姿旋转 A R B ^AR_B ARB
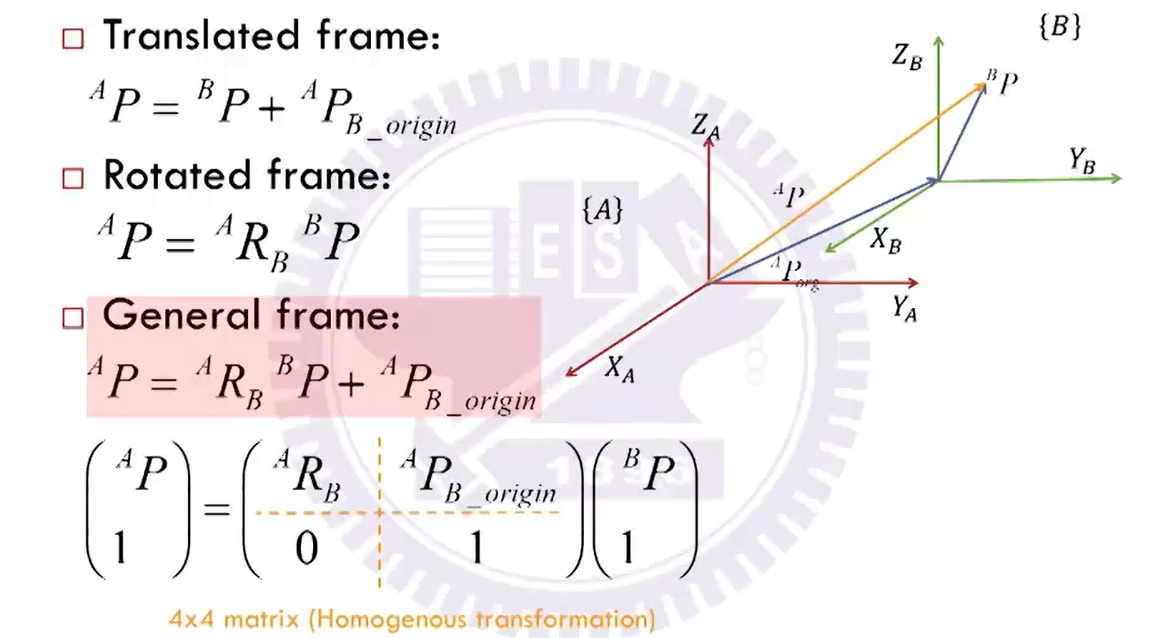
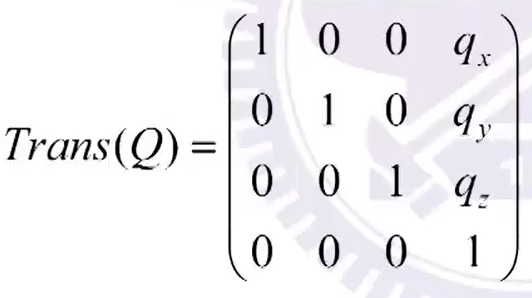
其中平移可交换,旋转非同轴不可交换
 旋转
旋转
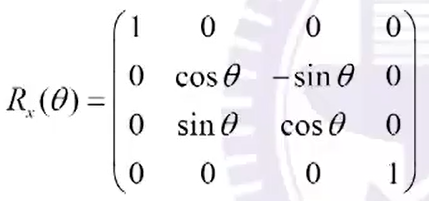
机器人关节变换
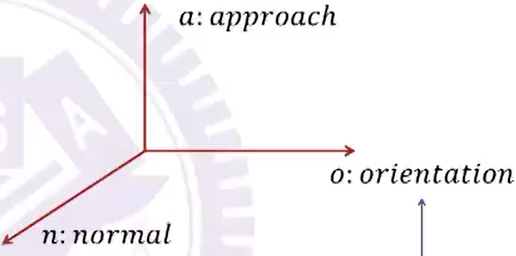
x : n , y : o , z : a x:n,\ \ y:o,\ \ z:a x:n, y:o, z:a
A P 2 = T ∗ A R 1 ^AP_2 = T *\ ^AR_1 AP2=T∗ AR1
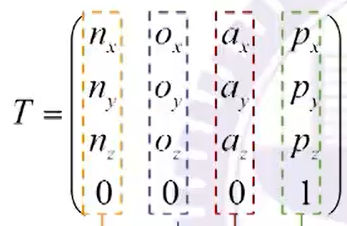
I n v e r s i o n : B T A = A T B − 1 Inversion:\ ^BT_A = \ ^AT_B^{-1} Inversion: BTA= ATB−1

前/后乘法
后乘法( p o s t m u l t i p l y postmultiply postmultiply): Y = A × B Y = A \times B Y=A×B 变换B时对A的坐标轴frame of A(机器臂采用)
前乘法( p r e m u l t i p l y premultiply premultiply): Y = B × A Y = B \times A Y=B×A 变换B时对基座坐标轴base coordinate frame
旋转矩阵
旋转变换关系 R K ( θ ) T = C R Z ( θ ) X = C R Z ( θ ) C − 1 T R_K(\theta)T = CR_Z(\theta)X = CR_Z(\theta)C^{-1}T RK(θ)T=CRZ(θ)X=CRZ(θ)C−1T
其中:地面T,坐标系C,二者变换关系 T = C X T=CX T=CX,C的Z轴在T中是K轴

可解出系数K
三轴PRY旋转: R P Y ( ϕ , θ , ψ ) = R Z ( ϕ ) R Y ( θ ) R X ( ψ ) RPY(\phi,\theta,\psi) = R_Z(\phi)R_Y(\theta)R_X(\psi) RPY(ϕ,θ,ψ)=RZ(ϕ)RY(θ)RX(ψ)

圆柱坐标Cylindrical Coordinates
c y l ( z , α , γ ) = t r a n s ( 0 , 0 , z ) ∗ R Z ( α ) ∗ T r a n s ( γ , 0 , 0 ) cyl(z,\alpha,\gamma) = trans(0,0,z)*R_Z(\alpha)*Trans(\gamma,0,0) cyl(z,α,γ)=trans(0,0,z)∗RZ(α)∗Trans(γ,0,0)
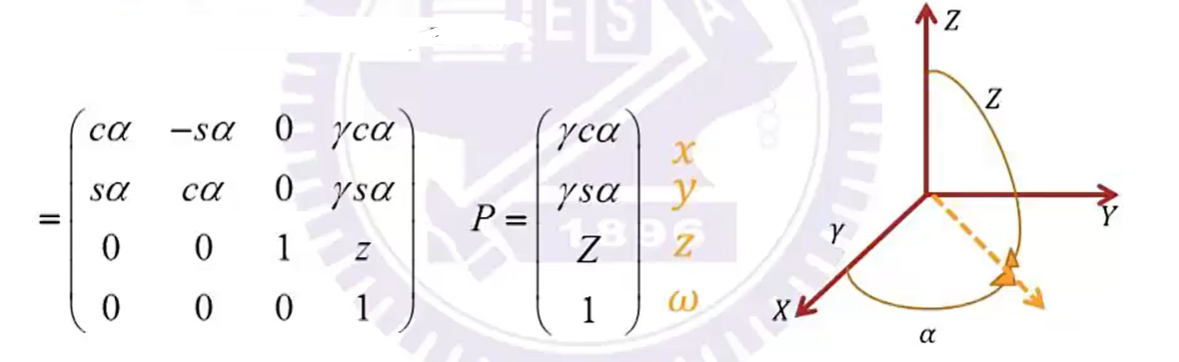
球坐标Spherical Coordinates
S ( α , β , γ ) = R Z ( α ) ∗ R Y ( γ ) ∗ T r a n s ( 0 , 0 , γ ) S(\alpha,\beta,\gamma) = R_Z(\alpha)*R_Y(\gamma)*Trans(0,0,\gamma) S(α,β,γ)=RZ(α)∗RY(γ)∗Trans(0,0,γ)

运动学
关注位置,速度,加速度,不考虑受力分析
运动方式:旋转Revolute 平移Prismatic
DH模型
六个参数 ⇒ \Rightarrow ⇒四个参数
关节角 θ \theta θ:关节旋转角度(关节旋转变量), θ i \theta_i θi为 x i x_i xi轴与 x i − 1 x_{i-1} xi−1轴夹角
连杆长度 a a a:两相邻关节轴的公垂线长度(固定参数), a i − 1 a_{i-1} ai−1为 z i z_i zi轴与 z i − 1 z_{i-1} zi−1轴公垂线长度
连杆偏置 d d d:两相邻x轴的距离(关节平移变量), d i d_i di为 x i x_i xi轴与 x i − 1 x_{i-1} xi−1轴距离
连杆扭转角 α \alpha α:连杆两端关节扭转角度(固定参数), α i − 1 \alpha_{i-1} αi−1为 z i z_i zi轴与 z i − 1 z_{i-1} zi−1轴夹角
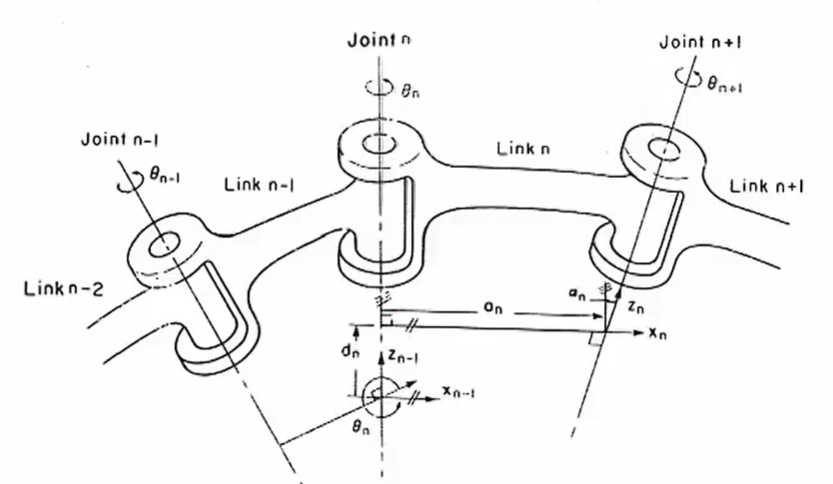
可计算相邻关节坐标变化关系:
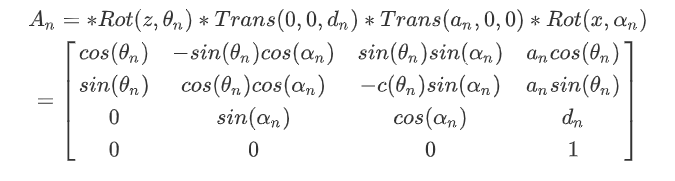
对地面 T n = A 1 A 2 A 3 . . . A n = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] = [ r p 0 1 ] T_n = A_1 A_2 A_3 ... A_n = \begin{bmatrix} n_x & o_x & a_x & p_x \\ n_y & o_y & a_y & p_y \\ n_z & o_z & a_z & p_z \\0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} r & p \\ 0 & 1 \end{bmatrix} Tn=A1A2A3...An=⎣⎢⎢⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎥⎥⎤=[r0p1],其中n为连杆link数
逆运动学IK
Inverse Kinematics
通过末端Tool Frame对应的 T n T_n Tn求解 θ 1 \theta_1 θ1 ~ θ n \theta_n θn
工作空间Workspace:所有末端Tool能够达到的位置
Dexterous Workspace:能够向所有方向运动的末端位置 ⇒ \Rightarrow ⇒灵活
Configuration:使末端到达一个点的方式(IK的解集)
反解算方式:代数法Algebraic(矩阵乘法解方程) vs 几何法Geometric(空间求解,四维以上需要拆分空间)
计算
三轴机器人中,为保证三个自由度,只能用矩阵第四列position求解(P6 49:46 没太听明白)
将 A 1 − 1 A_1^{-1} A1−1提前, A 1 − 1 T 3 = A 2 A 3 A_1^{-1} T_3 = A_2 A_3 A1−1T3=A2A3简化第四列计算
六轴机器人拆分成一二三轴确定位置,四五六轴球形轴确定方向
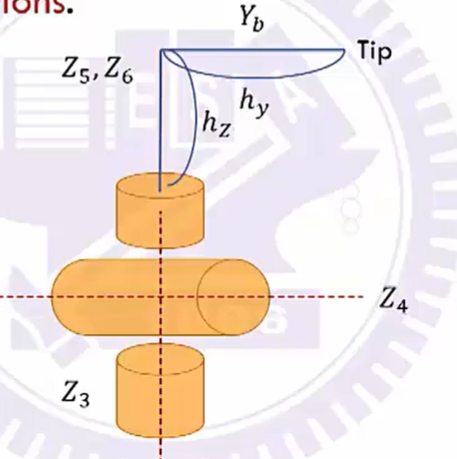
其中e表示end-effector,w表示wrist
通过末端位姿导出 h y h_y hy、 h z h_z hz,得到w坐标,得到 w h y ^wh_y why、 w h z ^wh_z whz,通过 w h z ^wh_z whz确定 θ 4 \theta_4 θ4、 θ 5 \theta_5 θ5使其影响被消除,通过 w h y ^wh_y why确定 θ 6 \theta_6 θ6
逆运动学对重复率、精确度非常重要 ⇒ \Rightarrow ⇒ 校正
微分关系
速度
坐标系变换:绝对=相对+牵连
极坐标:
x ⃗ = r e r ⃗ \vec{x}=r\vec{e_r} x=rer
v ⃗ = d x ⃗ d t = d r d t e r ⃗ + r d e r ⃗ d t = r ˙ e r ⃗ + ω r e θ ⃗ \vec{v} = \frac{d\vec{x}}{dt} = \frac{dr}{dt}\vec{e_r}+r\frac{d\vec{e_r}}{dt} = \dot{r}\vec{e_r}+\omega r\vec{e_{\theta}} v=dtdx=dtdrer+rdtder=r˙er+ωreθ
a ⃗ = d v ⃗ d t = d r ˙ d t e r ⃗ + r ˙ d e r ⃗ d t + d ω d t r e θ ⃗ + ω d r d t e θ ⃗ + ω r d e θ ⃗ d t = ( r ¨ − ω 2 r ) e r ⃗ + ( 2 ω r ˙ + ω ˙ r ) e θ ⃗ \vec{a} = \frac{d\vec{v}}{dt} = \frac{d\dot{r}}{dt}\vec{e_r}+\dot{r}\frac{d\vec{e_r}}{dt} + \frac{d\omega}{dt}r\vec{e_{\theta}} + \omega \frac{dr}{dt} \vec{e_{\theta}} +\omega r \frac{d\vec{e_{\theta}}}{dt} = (\ddot{r} - \omega^2r)\vec{e_r} + (2\omega\dot{r} + \dot{\omega}r)\vec{e_{\theta}} a=dtdv=dtdr˙er+r˙dtder+dtdωreθ+ωdtdreθ+ωrdtdeθ=(r¨−ω2r)er+(2ωr˙+ω˙r)eθ
矩阵:
平动 A V Q = d A Q d t = A ( B V Q ) + A V B o r g = B A R d B Q d t + A V B o r g = B A R B V Q + A V B o r g ^AV_Q= \frac{d^AQ}{dt} = \ ^A(^BV_Q)+\ ^AV_{Borg} = \frac{^A_BR\ d^BQ}{dt}+\ ^AV_{Borg} = \ ^A_BR\ ^BV_Q+\ ^AV_{Borg} AVQ=dtdAQ= A(BVQ)+ AVBorg=dtBAR dBQ+ AVBorg= BAR BVQ+ AVBorg
旋转 A V Q = A ( B V Q ) + A Ω B × A Q = B A R B V Q + A Ω B × ( A R B B Q ) ^AV_Q= \ ^A(^BV_Q)+\ ^A\Omega_B \times \ ^AQ = \ ^A_BR\ ^BV_Q + \ ^A\Omega_B \times(^AR_B \ ^BQ) AVQ= A(BVQ)+ AΩB× AQ= BAR BVQ+ AΩB×(ARB BQ)
总速度
KaTeX parse error: \tag works only in display equations
若连杆 i + 1 i+1 i+1相对于连杆 i i i的加速度绕 Z i Z_i Zi轴,用矩阵 P i + 1 ∗ = P i + 1 − P i P_{i+1}^*=P_{i+1}-P_{i} Pi+1∗=Pi+1−Pi表示连杆长度
角速度 W i + 1 = W i + W s = W i + Z i ⃗ q i + 1 ˙ W_{i+1}=W_i+W_s=W_i+\vec{Z_i}\dot{q_{i+1}} Wi+1=Wi+Ws=Wi+Ziqi+1˙
连杆 i + 1 i+1 i+1速度
KaTeX parse error: \tag works only in display equations
Jacobian矩阵
在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。
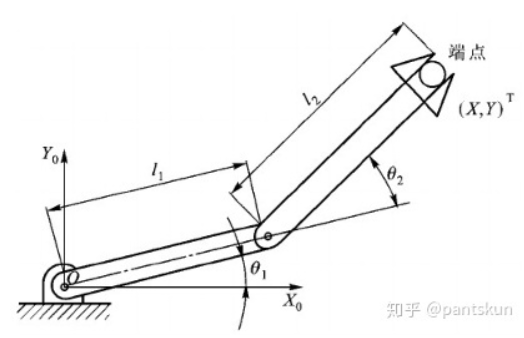
上图中端点位置坐标KaTeX parse error: \tag works only in display equations
雅各比矩阵 J = [ ∂ X ∂ θ 1 ∂ X ∂ θ 2 ∂ Y ∂ θ 1 ∂ Y ∂ θ 2 ] J = \begin{bmatrix} \frac{\partial X}{\partial \theta_1} & \frac{\partial X}{\partial \theta_2} \\ \frac{\partial Y}{\partial \theta_1} & \frac{\partial Y}{\partial \theta_2} \end{bmatrix} J=[∂θ1∂X∂θ1∂Y∂θ2∂X∂θ2∂Y]是函数 X , Y X,Y X,Y对于 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2的偏导数矩阵
则有微分形式 d V = [ d X d Y ] = J [ d θ 1 d θ 2 ] dV = \begin{bmatrix} dX \\ dY \end{bmatrix} = J \begin{bmatrix} d\theta_1 \\ d\theta_2 \end{bmatrix} dV=[dXdY]=J[dθ1dθ2],简写为 d V = J d θ dV = J d\theta dV=Jdθ
本课程中表示为 d X = J d q dX=Jdq dX=Jdq
其中 X = f ( q ) X=f(q) X=f(q), d X = [ d x d y d z δ x δ y δ z ] T dX=[dx\ dy\ dz\ \delta x\ \delta y\ \delta z]^T dX=[dx dy dz δx δy δz]T, d q = [ d θ 1 d θ 1 . . . d θ n ] T dq=[d\theta_1\ d\theta_1\ ...\ d\theta_n]^T dq=[dθ1 dθ1 ... dθn]T
d X d t = d f ( q ) d t = d f ( q ) d q × d q d t \frac{dX}{dt} = \frac{df(q)}{dt} = \frac{df(q)}{dq} \times \frac{dq}{dt} dtdX=dtdf(q)=dqdf(q)×dtdq可得到 X ˙ = J q ˙ \dot{X}=J \dot{q} X˙=Jq˙
P O S = B A S E ∗ T N ∗ T O O L POS=BASE*T_N*TOOL POS=BASE∗TN∗TOOL
解 J − 1 J^{-1} J−1可以得到 d q = J − 1 d X dq=J^{-1}dX dq=J−1dX,或者找微分关系求 d θ i d\theta_i dθi
J w r i s t = [ J 1 0 J 2 0 ] J^{wrist}= \begin{bmatrix} J_1 & 0 \\ J_2 & 0\end{bmatrix} Jwrist=[J1J200], J − 1 = [ J 1 ] − 1 [ J 3 ] − 1 J^{-1}=[J_1]^{-1}[J_3]^{-1} J−1=[J1]−1[J3]−1
神经网络算法求解IK或者 J − 1 J^{-1} J−1:相近输入会导致相近输出;规则越多越精细但计算复杂
微分
T + d T = T r a n s ( d x , d y , d z ) ∗ R o t ( k , d θ ) ∗ T T+dT=Trans(dx,dy,dz)*Rot(k,d\theta)*T T+dT=Trans(dx,dy,dz)∗Rot(k,dθ)∗T得到 Δ ∗ T \Delta^*T Δ∗T
d
θ
d\theta
dθ小角近似得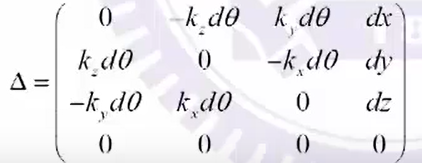
若 R o t ( k , d θ ) Rot(k,d\theta) Rot(k,dθ)表示为 R o t ( x , δ x ) ∗ R o t ( y , δ y ) ∗ R o t ( z , δ z ) Rot(x,\delta x)*Rot(y,\delta y)*Rot(z,\delta z) Rot(x,δx)∗Rot(y,δy)∗Rot(z,δz)
其中 δ x = k x d θ \delta x = k_x d\theta δx=kxdθ, δ y = k y d θ \delta y = k_y d\theta δy=kydθ, δ z = k z d θ \delta z = k_z d\theta δz=kzdθ

在六轴机器人中 T n = A 1 A 2 A 3 . . . A n T_n = A_1 A_2 A_3 ... A_n Tn=A1A2A3...An
旋转轴:(1)式对关节角求微分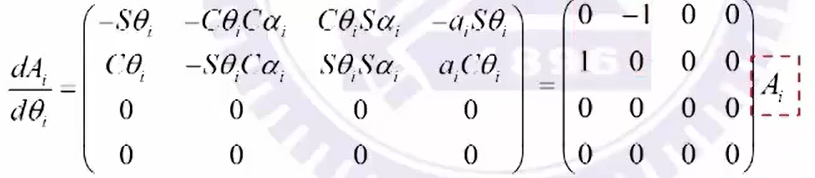
平行轴:(1)式对连杆偏置求微分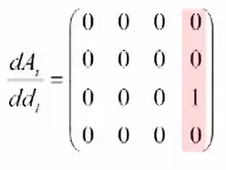
i − 1 Δ i ^{i-1}\Delta_i i−1Δi:旋转轴 i − 1 d i = 0 ^{i-1}d_i=0 i−1di=0, i − 1 δ i = [ 0 0 1 ] T ^{i-1}\delta_i=[0\ 0\ 1]^T i−1δi=[0 0 1]T;平行轴 i − 1 δ i = 0 ^{i-1}\delta_i=0 i−1δi=0, i − 1 d i = [ 0 0 1 ] T ^{i-1}d_i=[0\ 0\ 1]^T i−1di=[0 0 1]T
T n + d T n = A 1 ∗ A 2 . . . ∗ ( A i + d A i ) ∗ . . . ∗ A n = T n + ( A 1 ∗ A 2 . . . ∗ A i − 1 ∗ i − 1 Δ i A i ∗ A i + 1 ∗ . . . ∗ A n ) d q i T_n+dT_n = A_1*A_2...*(A_i+dA_i)*...*A_n \\= T_n + (A_1*A_2...*A_{i-1}*\ ^{i-1}\Delta_iA_i*A_{i+1}*...*A_n)dq_i Tn+dTn=A1∗A2...∗(Ai+dAi)∗...∗An=Tn+(A1∗A2...∗Ai−1∗ i−1ΔiAi∗Ai+1∗...∗An)dqi
写成形式:
d
T
n
=
T
n
∗
T
n
Δ
i
∗
d
q
i
(4)
dT_n=T_n*\ ^{T_n}\Delta_i*dq_i\tag{4}
dTn=Tn∗ TnΔi∗dqi(4)
则有
T
n
Δ
i
=
U
i
−
1
−
1
∗
i
−
1
Δ
i
∗
U
i
−
1
^{T_n}\Delta_i=U_{i-1}^{-1}*\ ^{i-1}\Delta_i*U_{i-1}
TnΔi=Ui−1−1∗ i−1Δi∗Ui−1,其中
U
i
−
1
=
A
i
∗
…
∗
A
n
U_{i-1}=A_i*…*A_n
Ui−1=Ai∗…∗An
代入旋转轴和平行轴(P10 27.04 没看懂)
x : n , y : o , z : a x:n,\ \ y:o,\ \ z:a x:n, y:o, z:a
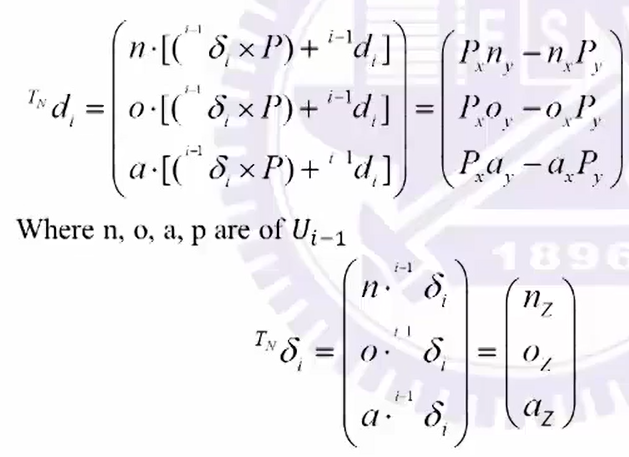
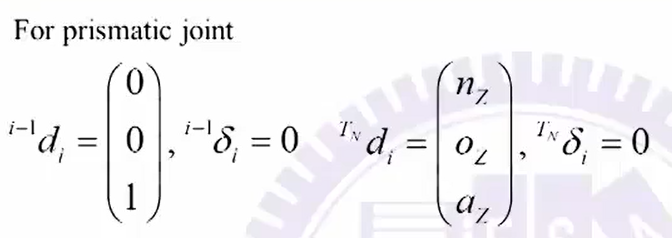
工业上粗略估计:已知 d T 6 dT_6 dT6, T 6 n = T 6 + d T 6 ⇒ T T Δ = δ T Δ δ q δ q T^n_6=T_6+dT_6 \Rightarrow T\ ^T\Delta=\frac{\delta T \Delta}{\delta q} \delta q T6n=T6+dT6⇒T TΔ=δqδTΔδq
然后通过 T 6 n T^n_6 T6n计算新的关节方案 d q = q n − q dq=q^n-q dq=qn−q
运动规划
考虑因素:易于指定,位置速度连续,奇点的处理,configuration统一,坐标系(关节/笛卡尔)
路径描述:起点、终点、经过点的位姿(position&orientation)
多项式路径规划
约束:起点、终点的位置、速度 ⇒ \Rightarrow ⇒三次及以上多项式
路径规划:最短路径/最短时间,相切得平滑曲线
系统复杂度提高:B-spline planning提高多项式次数,Bezier Cune增加路径点数
对称:减少一个约束
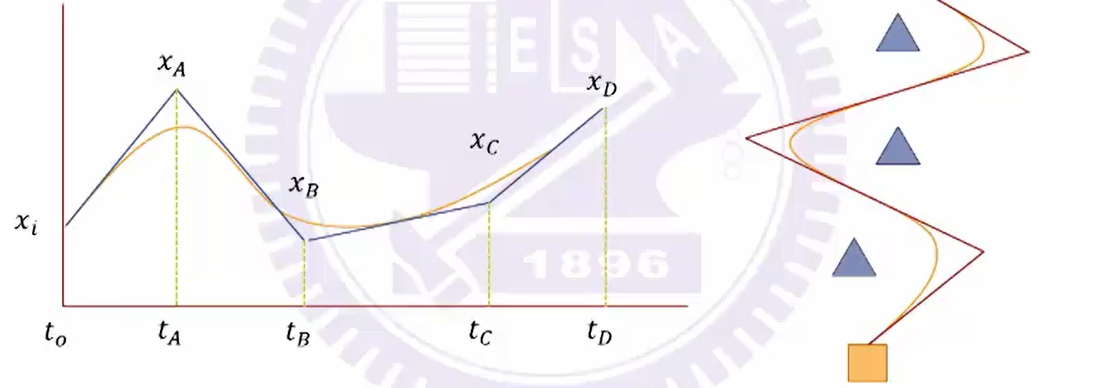
A、B位置连续、速度连续、加速度为0,共6个约束,对称减少一个,五次多项式解方程即可
坐标系
通常在笛卡尔坐标系中做路径规划,逆运动学计算复杂,需要考虑奇点( J J J不可逆)。
关节坐标系虽然计算调用方便,没有奇点和configuration问题,但是转化为笛卡尔坐标位置时较复杂。将路径点映射到关节坐标系进行规划,但是受限于关节之间的牵连,速度取决于最慢的关节。
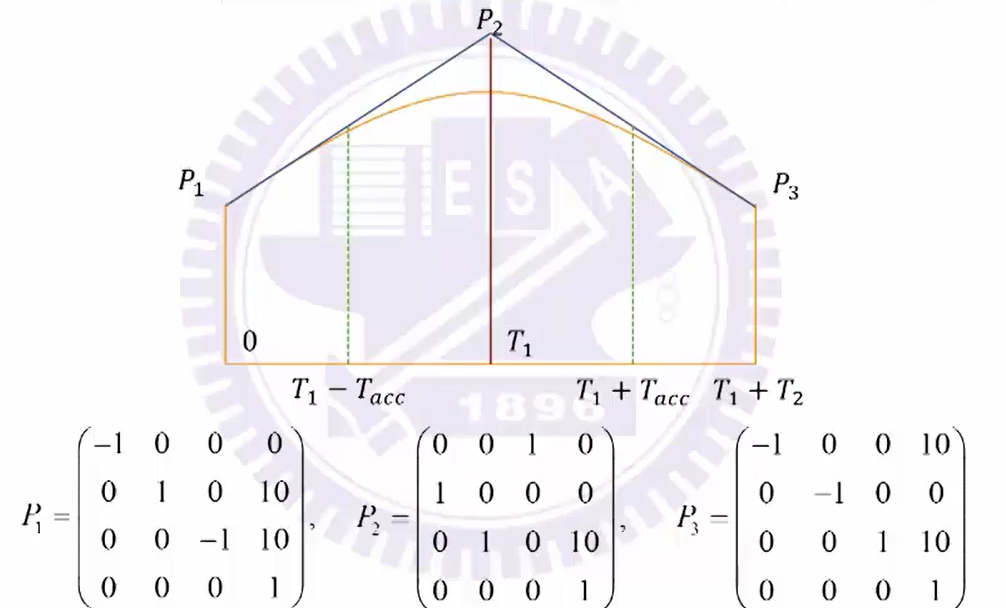
从POS1到POS2的规划:
T 6 1 = B A S E − 1 ∗ P O S 1 ∗ T O O L − 1 T_6^1=BASE^{-1}*POS1*TOOL^{-1} T61=BASE−1∗POS1∗TOOL−1
T 6 2 = B A S E − 1 ∗ P O S 2 ∗ T O O L − 1 T_6^2=BASE^{-1}*POS2*TOOL^{-1} T62=BASE−1∗POS2∗TOOL−1
T 6 = B A S E − 1 ∗ P O S 1 ∗ D ( r ) ∗ T O O L − 1 T_6=BASE^{-1}*POS1*D(r)*TOOL^{-1} T6=BASE−1∗POS1∗D(r)∗TOOL−1
令自变量 r = t T r=\frac{t}{T} r=Tt,有 0 ⩽ r ⩽ 1 0\leqslant r \leqslant 1 0⩽r⩽1, D ( 0 ) = 1 D(0)=1 D(0)=1, D ( 1 ) = P O S 1 − 1 ∗ P O S 2 D(1)=POS1^{-1}*POS2 D(1)=POS1−1∗POS2
D ( r ) = T r a n s l i n e ( r ) ∗ R a z ( r ) ∗ R o x y ( r ) D(r)=Trans_{line}(r)*Ra_z(r)*Ro_{xy}(r) D(r)=Transline(r)∗Raz(r)∗Roxy(r)
其中从POS1到POS2的平移 T r a n s l i n e ( r ) = [ 1 0 0 r x 0 1 0 r y 0 0 1 r z 0 0 0 1 ] Trans_{line}(r)=\begin{bmatrix} 1&0&0&r_x \\ 0&1&0&r_y \\ 0&0&1&r_z \\ 0&0&0&1 \end{bmatrix} Transline(r)=⎣⎢⎢⎡100001000010rxryrz1⎦⎥⎥⎤
使得两个
Z
Z
Z轴重合的旋转
R
a
z
(
r
)
=
Ra_z(r)=
Raz(r)=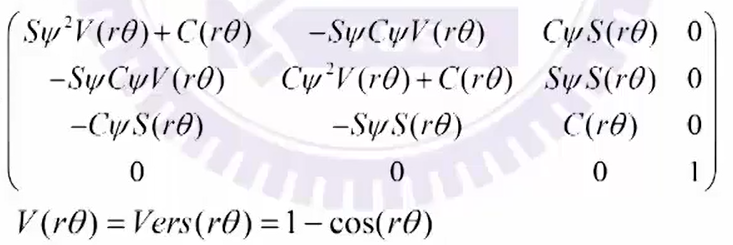
其中旋转角度为 θ \theta θ,旋转轴为 K K K轴(为 P O S 1 POS1 POS1的 Y Y Y轴绕 Z Z Z轴旋转 ψ \psi ψ角度)
使得两个 Y Y Y轴重合的旋转 R o z ( r ) = [ C ( r ϕ ) − S ( r ϕ ) 0 0 S ( r ϕ ) C ( r ϕ ) 0 0 0 0 1 0 0 0 0 1 ] Ro_z(r)=\begin{bmatrix} C(r\phi)&-S(r\phi)&0&0 \\ S(r\phi)&C(r\phi)&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{bmatrix} Roz(r)=⎣⎢⎢⎡C(rϕ)S(rϕ)00−S(rϕ)C(rϕ)0000100001⎦⎥⎥⎤
变量: x , y , z , ψ , θ , ϕ x,y,z,\psi,\theta,\phi x,y,z,ψ,θ,ϕ,表达式 D ( r ) = [ n x ( . . . ) C ψ S ( r θ ) r x n y ( . . . ) S ψ S ( r θ ) r y n z ( . . . ) C ( r θ ) r z 0 0 0 1 ] D(r)=\begin{bmatrix} n_x&(...)&C\psi S(r\theta)&r_x \\ n_y&(...)&S\psi S(r\theta)&r_y \\ n_z&(...)&C(r\theta)&r_z \\ 0&0&0&1 \end{bmatrix} D(r)=⎣⎢⎢⎡nxnynz0(...)(...)(...)0CψS(rθ)SψS(rθ)C(rθ)0rxryrz1⎦⎥⎥⎤
R a z ( 1 ) Ra_z(1) Raz(1)代入 r = 1 r=1 r=1求 ψ , θ \psi,\theta ψ,θ; R o y ( 1 ) Ro_y(1) Roy(1)代入 r = 1 r=1 r=1求 ϕ \phi ϕ;
( x : n , y : o , z : a x:n,\ \ y:o,\ \ z:a x:n, y:o, z:a)


例:
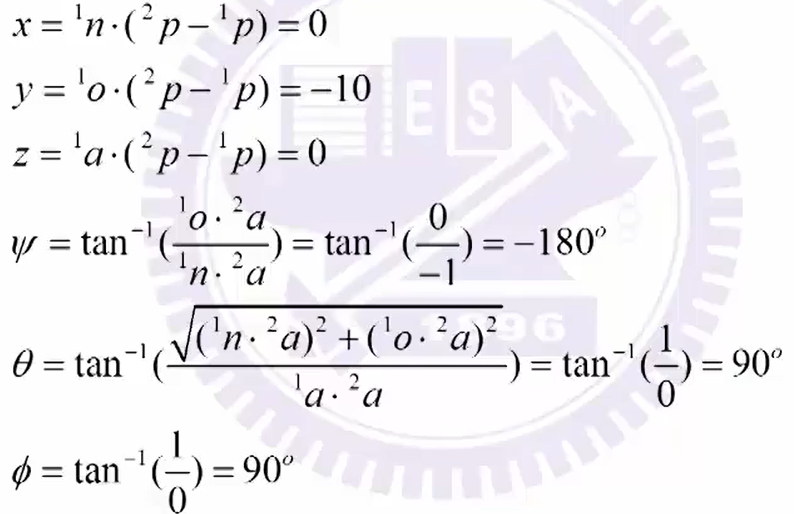
位姿空间方法
运动规划,路径规划,轨迹规划
躲避障碍方式:
①根据障碍形状抽象为一系列圆形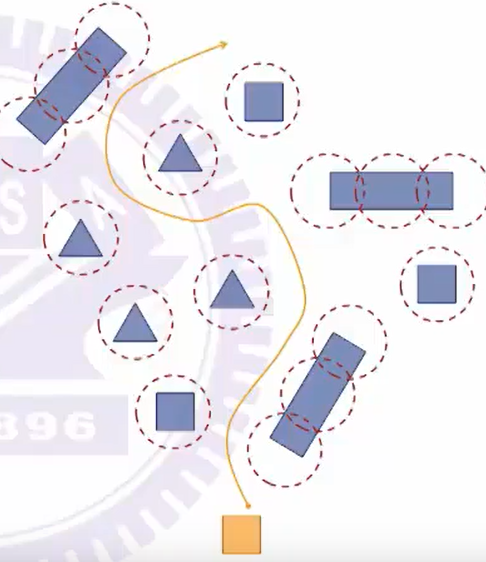
②人工势场法:建立势场模型,障碍物为高势能,目的地为低势能
缺点:容易被势阱或者壁垒困住 ⇒ \Rightarrow ⇒给一个“冲量”
③地毯式搜索:末端连杆开始向下,每个连杆左右来回试探,recursive递归$基础上优化
优化:只需要精确无障碍空间,遇到障碍物时增大试探间隔;放弃探索狭窄区域,选择宽敞路径;对不同类型道路加权,最后选择分数最高路径;456短轴球空间不考虑,只用123轴试探。
总结:先建地图,根据地图找路径比较 vs 物理模型





















 1255
1255











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








