【评分尺度变换方法】评分卡评分尺度变换的两种方法

最新推荐文章于 2022-07-04 22:33:10 发布

RyanZhengrp

最新推荐文章于 2022-07-04 22:33:10 发布

阅读量5.1k

点赞数 2

分类专栏：风控文章标签：风控算法

本文链接：https://blog.csdn.net/xiezhen_zheng/article/details/107300444

版权

风控专栏收录该内容

0 篇文章

订阅专栏

本文深入解析了将模型预测概率值转换为信用评分的过程，包括逻辑回归模型的应用、评分标尺的设定及分数与违约概率的关系，适用于风控领域的专业人士。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

大家在市面上常见的信用分、欺诈分、营销分都是以如下方式展现的。如：

1. 芝麻分的分值范围为350至950，分值越高代表信用越好，相应违约率相对较低，较高的芝麻分可以帮助用户获得更高效、更优质的服务（http://www.xin.xin/#/detail/1-2-0）；

2. 集奥的信用分范围为300至900，分数越高, 说明客户的信用风险越小；

3. 百融的信用分范围为300至1000，分数越高, 说明客户的信用风险越小；

4. 同盾智信分范围为300至900，分数越高, 说明客户的信用风险越小；

5. FICO分的分值范围为300至850，分数越高, 说明客户的信用风险越小。

那么需要怎么将逻辑回归/xgboost等树模型的概率值映射为这种整数形式的分数呐？相信各位有风控经验的童鞋已是耳熟能详咯！此篇文章与大伙一起回顾下将模型预测出来的概率值通过评分标尺转化为市面上常见的分数形式。有错误之处欢迎大伙交流校正！！！

文章目录：

章节 1. 基于逻辑回归构建评分卡模型流程

章节 2. 模型概率值转分

章节 3. 单个变量得分加总转分

章节 4. 小结

章节 1. 基于逻辑回归构建评分卡模型流程

这里从step 3开始介绍。后续会写一篇完整的基于逻辑回归构建评分卡模型的流程系列文章

章节 1. 基于逻辑回归构建评分卡模型流程

基于逻辑回归构建评分卡的流程，主要包含如下：

step 1 ：目标变量的构建

step 2 ：特征工程

step 3 ：变量分箱，WOE值映射

step 4 ：特征选择

step 5 ：模型拟合(即变量参数估计)

step 6 ：概率值到评分卡标准分转化

这里从step 3开始介绍。后续会写一篇完整的基于逻辑回归构建评分卡模型的流程系列文章

1. 变量分箱，WOE值映射

1.1 变量分箱：

常见的变量分箱方法有如下几种

1.1.1 等频分箱

1.1.2 等距分箱

1.1.3 kmeans分箱

1.1.4 决策树分箱

1.1.5 卡方分箱

1.1.6 iv差值最小化分箱

1.1.7 单调相邻池化分箱

1.2 WOE值映射，要对一个变量进行 WOE 编码，需要首先把这个变量进行分组处理。分组后，对于第 i 组，WOE 的计算公式如下:

1.2.1 WOE第一种公式计算方式

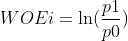
$WOEi = \ln (\frac{p1}{p0})$

其中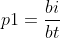： $p1=\frac{bi}{bt}$ ，为该变量第i组的坏客户数量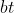，为样本整体的坏客户数量；

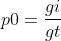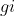$p0=\frac{gi}{gt}$ ，为该变量第i组的好客户数量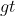，为样本整体的好客户数量

把p1和p0带入公式，得到第一种计算方式：

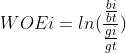
$WOEi = ln(\frac{\frac{bi}{bt}}{\frac{gi}{gt}})$

1.2.2 WOE第二种公式计算方式

$WOEi = ln(\frac{\frac{bi}{bt}}{\frac{gi}{gt}})=ln(\frac{\frac{bi}{gi}}{\frac{bt}{gt}})$

变换以后我们可以看出，WOE 也可以这么理解，它表示的是当前这个组中好坏客户的比值，和在所有样本中这个比值的差异。这个差异是用这两个比值的比值，再取对数来表示的。WOE 越大，这种差异越大，这个分组里的样本整体坏的可能性就越大，WOE 越小，差异越小，这个分组里的样本整体坏的可能性就越小。

小tips：如果你在计算WOE时，是bad做分子，那么在进行逻辑回归参数估计的时候，选用的变量时需要注意选用变量参数为+号的变量；反之，如果good做分子，选用的变量时需要注意选用变量参数为-号的变量

2. 特征选择

2.1 IV

2.2 相关系数

2.3 VIF

2.4 特征稳定性（查看psi和该变量的badrate或woe在测试集或oot的表现趋势和在训练集是否保持一致）

2.5 业务可解释性

2.6 逐步回归

3. 模型拟合(即变量参数估计)

逻辑回归的公式：

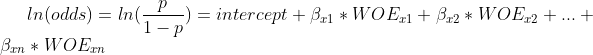
$ln(odds)=ln(\frac{p}{1-p})=intercept + \beta _{x1}*WOE_{x1}+ \beta _{x2}*WOE_{x2}+...+ \beta _{xn}*WOE_{xn}$

其中xn表示第n个入模变量

如上我们得到了线性组合的结果，在将结果套入sigmoid函数，即得到逻辑回归模型预测出来的概率值。那么如何将概率值转化到评分卡标准分形式呐？小伙伴们，重点来咯！！！

4. 概率值到评分卡标准分转化

将模型的概率值转化为评分卡标准分形式的目的：

1. 放大原始概率值的间距，对于原始0-1之间的概率值拉开，便于理解即业务层面制定相关策略

2. 整数分更易于理解，赋予其Odds业务含义，并且可指定分数区间

其实概率值到评分卡标准分转化是一个线性变换，在这个线性变换的过程中，我们需要通过评分标尺（scaling parameters）来设定评分卡的分值刻度，可以通过将分值表示为比率(坏好比率)对数的线性表达式来定义，即可表示为下式:

Score = A - B*ln(odds)

由逻辑回归的基本原理，我们将客户违约的概率表示为 p，则正常的概率为 1-p。因此，可以得到:

$odds=\frac{p}{1-p}$

其中，A 和 B 是常数（即风控童鞋比较熟悉的A(offset)、B(factor)），ln(odds)为如上逻辑回归公式。式中的减号可以使得违约概率越低，得分越高。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。

章节 2. 模型概率值转分

在实际应用中，A(offset)、B(factor)这两个参数难以解释，因此也不方便指定初始值。更常用的是事先指定下述三个参数：

odds 基准odds(坏好比)：与真实违约概率对应，可换算得到违约概率
base_score 基准分值：在基准odds对应的信用分（odds at base point）
pdo (point double odds)：当odds变成2倍时，对应评分所增加的分数

根据以上的分析，我们首先假设坏好比率 odds 的特定点的分值为 Score。则比率为 2倍odds 的点的分值应该为 Score+pdo。代入式中，可以得到如下两个等式:

Score = A - B*ln(odds)

Score-pdo = A - B*ln(2odds) #因为odds是坏好比(p/1-p)，并且score是越小越坏，所以此处由原来的Score+pdo变成Score-pdo。

接着根据如上两个公式可得出：

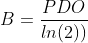
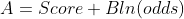
$B=\frac{PDO}{ln(2))}$ A=Score+Bln(odds)

现以具体数字来说明。假设我们希望展现的信用分base_score为600时，对应的odds（坏好比率）为1:15。而当odds增加1倍至2:15时，信用分降低50分至550分（pdo=50）。那么代入式中可求得B、A：

pdo = 50         # pdo (points to double the odds)
base_score = 600 # 基准分数
odds = 1/15        # odds, 坏好比
 
import numpy as np
B = pdo / np.log(2)  
A = base_score + B * np.log(odds)

根据 A 和 B 的值，可以轻松的计算出如下表的分数刻度表（分数、坏好比率、客户违约概率）:

分数	odds		PD(客户逾期概率)
1480	1	2980020	0.00003%
1460	1	2258433	0.00004%
1440	1	1711572	0.00006%
1420	1	1297129	0.00008%
1400	1	983040	0.00010%
1380	1	745005	0.00013%
1360	1	564608.2	0.00018%
1340	1	427893	0.00023%
1320	1	324282.3	0.00031%
1300	1	245760	0.00041%
1280	1	186251.3	0.00054%
1260	1	141152.1	0.00071%
1240	1	106973.3	0.00093%
1220	1	81070.57	0.00123%
1200	1	61440	0.00163%
1180	1	46562.81	0.00215%
1160	1	35288.01	0.00283%
1140	1	26743.31	0.00374%
1120	1	20267.64	0.00493%
1100	1	15360	0.00651%
1080	1	11640.7	0.00859%
1060	1	8822.003	0.01133%
1040	1	6685.828	0.01495%
1020	1	5066.91	0.01973%
1000	1	3840	0.02603%
980	1	2910.176	0.03435%
960	1	2205.501	0.04532%
940	1	1671.457	0.05979%
920	1	1266.728	0.07888%
900	1	960	0.10406%
880	1	727.544	0.13726%
860	1	551.3752	0.18104%
840	1	417.8643	0.23874%
820	1	316.6819	0.31478%
800	1	240	0.41494%
780	1	181.886	0.54679%
760	1	137.8438	0.72023%
740	1	104.4661	0.94817%
720	1	79.17047	1.24734%
700	1	60	1.63934%
680	1	45.4715	2.15186%
660	1	34.46095	2.82000%
640	1	26.11652	3.68779%
620	1	19.79262	4.80940%
600	1	15	6.25000%
580	1	11.36787	8.08546%
560	1	8.615238	10.40016%
540	1	6.529129	13.28175%
520	1	4.948155	16.81194%
500	1	3.75	21.05263%
480	1	2.841969	26.02832%
460	1	2.153809	31.70769%
440	1	1.632282	37.98985%
420	1	1.237039	44.70195%
400	1	0.9375	51.61290%
380	1	0.710492	58.46271%
360	1	0.538452	65.00039%
340	1	0.408071	71.01917%
320	1	0.30926	76.37904%
300	1	0.234375	81.01266%
280	1	0.177623	84.91682%
260	1	0.134613	88.13577%
240	1	0.102018	90.74265%
220	1	0.077315	92.82337%
200	1	0.058594	94.46494%
180	1	0.044406	95.74823%
160	1	0.033653	96.74424%
140	1	0.025504	97.51299%
120	1	0.019329	98.10378%
100	1	0.014648	98.55630%
80	1	0.011101	98.90204%
60	1	0.008413	99.16569%
40	1	0.006376	99.36643%
20	1	0.004832	99.51911%
0	1	0.003662	99.63513%

未完待续！！！