在很多机器学习算法中,都会遇到最优化问题。因为我们机器学习算法,就是要在模型空间中找到这样一个模型,使得这个模型在一定范围内具有最优的性能表现。因此,机器学习离不开最优化。然而,对于很多问题,我们并不总能够找到这个最优,很多时候我们都是尽力去找到近似最优,这就是解析解和近似解的范畴。
很多最优化问题都是在目标函数是凸函数或者凹函数的基础上进行的。原因很简单,凸函数的局部极小值就是其全局最小值,凹函数的局部极大值就是其全局最大值。因此,只要我们依据一个策略,一步步地逼近这个极值,最终肯定能够到达全局最值附近。
那么,如何判断目标函数凸或者凹呢?
判断目标函数凸或者凹的方法
1 暴力计算法
这个方法是我自己起的名字,哈哈,但是方法不是我发明的。。所谓暴力计算法,就是直接对目标函数进行计算,然后判断其是否凸。具体地,就是计算目标函数的一阶导数和二阶导数。然后作出判断。
凸函数的一阶充要条件
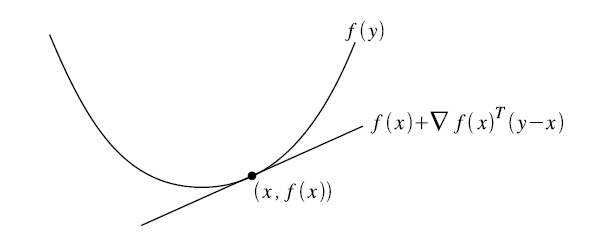
等号右边是对函数在x点的一阶近似。这个条件的意义是,对于函数在定义域的任意取值,函数的值都大于或者等于对函数在这点的一阶近似。用图来说明就是:
通过图可以很清楚地理解这个充要条件,但是,具体在应用中,我们不可能对每一个点都去计算函数的一阶导数








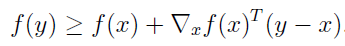
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1195
1195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








