1.微积分基本定理A
2.微积分基本定理B
1.微积分基本定理A
1).明白F(x)是什么
a.你有一条曲线, 它的方程是y = f(t)
b.a是一个固定不变的起点(比如 t = 0)
c.x是一个可以左右移动的终点
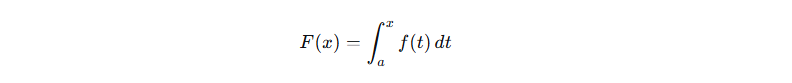
该积分的意义: 计算从固定起点t = a, 到可变终点t = x之间, 曲线f(t)之下的面积

2).F(x)的变化率是多少
想象你正在用一把高度不断变化的刷子, 从左向右粉刷这堵墙
a.F(x)表示你已经刷过的总面积
b.你现在站在x点, 当你再向右移动一个"极其微小的距离dx"时, 你新刷出来的那一小"条"面积是多少
c.新刷的那一小条, 高度就是你当前所在位置x的刷子高度, 也就是f(x), 宽度就是dx
d.所以新的面积是 ≈ f(x) * dx


2.微积分基本定理B
若函数f(x)在区间[a, b]上连续, 且F(x)是f(x)在[a, b]上的任意一个原函数(即F′(x) = f(x)), 则:
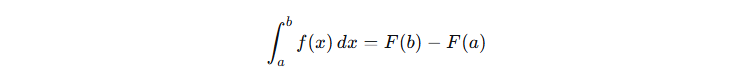
a.左边: ∫ₐᵇ f(x)dx表示函数f(x)从x = a到x = b的定积分
几何上可以理解为曲线y = f(x)在[a, b]上与x轴围成的"有向面积"
b.右边: F(b) − F(a), 其中F(x)是f(x)的任意一个原函数(即满足F'(x) = f(x)的函数)
整个公式的意思是: "要计算定积分, 只需找到被积函数f(x)的一个原函数F(x), 然后计算它在上下限的函数值之差"
为什么是"F(b) − F(a)"
想象一个物体沿直线运动, 设f(t)是物体在时刻t的瞬时速度
a.那么它的原函数F(t)就是物体从某个起点开始到时刻t的位移
b.物体从时刻a到时刻b的总位移变化, 显然就是F(b) − F(a)
c.另一方面, 总位移变化也可以通过把每瞬间的速度累加起来得到, 即 ∫ₐᵇ f(t) dt。
d.∫ₐᵇ f(t) dt = F(b) − F(a)
关键: "原函数F(x)记录了累积量, 而定积分是增量, 这个增量就是累积量在区间两端的差值"
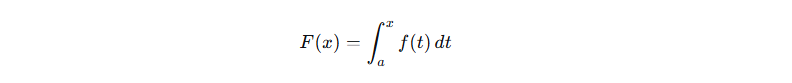



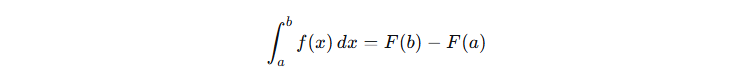





















 1921
1921

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








