蚁群算法（ACO）最短路径规划（MATLAB）

最新推荐文章于 2024-04-01 10:30:21 发布

Reacubeth

最新推荐文章于 2024-04-01 10:30:21 发布

阅读量6.5w

点赞数 83

分类专栏：机器学习 MATLAB 机器学习徐奕的专栏文章标签： MATLAB 蚁群算法机器学习

本文链接：https://blog.csdn.net/xyisv/article/details/79184815

版权

徐奕的专栏同时被 3 个专栏收录

228 篇文章 35 订阅

订阅专栏

机器学习

89 篇文章 19 订阅

订阅专栏

机器学习

57 篇文章 19 订阅

订阅专栏

蚁群算法最早是由Marco Dorigo等人在1991年提出，他们在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，据此提出了基于信息正反馈原理的蚁群算法。

蚁群算法根据模拟蚂蚁寻找食物的最短路径行为来设计的仿生算法，因此一般而言，蚁群算法用来解决最短路径问题，并真的在旅行商问题（TSP，一个寻找最短路径的问题）上取得了比较好的成效。目前，也已渐渐应用到其他领域中去，在图着色问题、车辆调度问题、集成电路设计、通讯网络、数据聚类分析等方面都有所应用。

具体概述及通用MATLAB代码请见： http://www.omegaxyz.com/2018/01/26/aco/ ‎

下面是蚁群算法机器人最短路径规划问题的MATLAB代码

（1代表障碍物）

function main() 
G=[0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
   0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0; 
   0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;];
MM=size(G,1);                  	   % G 地形图为01矩阵，如果为1表示障碍物 
Tau=ones(MM*MM,MM*MM);        % Tau 初始信息素矩阵
Tau=8.*Tau; 
K=100;                       	   %迭代次数（指蚂蚁出动多少波）
M=50;                        	   %蚂蚁个数
S=1 ;                         	   %最短路径的起始点
E=MM*MM;                        %最短路径的目的点
Alpha=1;                      	   % Alpha 表征信息素重要程度的参数
Beta=7;                       	   % Beta 表征启发式因子重要程度的参数
Rho=0.3 ;                      	   % Rho 信息素蒸发系数
Q=1;                               % Q 信息素增加强度系数 
minkl=inf; 
mink=0; 
minl=0; 
D=G2D(G); 
N=size(D,1);               %N表示问题的规模（象素个数）
 a=1;                     %小方格象素的边长
 Ex=a*(mod(E,MM)-0.5);    %终止点横坐标
 if Ex==-0.5 
Ex=MM-0.5; 
end 
Ey=a*(MM+0.5-ceil(E/MM)); %终止点纵坐标
 Eta=zeros(N);             %启发式信息，取为至目标点的直线距离的倒数
 %以下启发式信息矩阵
 for i=1:N 
 ix=a*(mod(i,MM)-0.5); 
   if ix==-0.5 
   ix=MM-0.5; 
   end 
iy=a*(MM+0.5-ceil(i/MM));  
   if i~=E 
   Eta(i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5; 
   else 
   Eta(i)=100; 
   end 
end 
ROUTES=cell(K,M);     %用细胞结构存储每一代的每一只蚂蚁的爬行路线
PL=zeros(K,M);         %用矩阵存储每一代的每一只蚂蚁的爬行路线长度
                      %启动K轮蚂蚁觅食活动，每轮派出M只蚂蚁
for k=1:K 
for m=1:M 
%状态初始化
W=S;                  %当前节点初始化为起始点
Path=S;                %爬行路线初始化
PLkm=0;               %爬行路线长度初始化
TABUkm=ones(N);       %禁忌表初始化
TABUkm(S)=0;          %已经在初始点了，因此要排除
DD=D;                 %邻接矩阵初始化
%下一步可以前往的节点
DW=DD(W,:); 
DW1=find(DW); 
for j=1:length(DW1) 
   if TABUkm(DW1(j))==0 
      DW(DW1(j))=0; 
  end 
end 
LJD=find(DW); 
Len_LJD=length(LJD);%可选节点的个数
%蚂蚁未遇到食物或者陷入死胡同或者觅食停止
while W~=E&&Len_LJD>=1 
%转轮赌法选择下一步怎么走
PP=zeros(Len_LJD); 
for i=1:Len_LJD 
    PP(i)=(Tau(W,LJD(i))^Alpha)*((Eta(LJD(i)))^Beta); 
end 
sumpp=sum(PP); 
PP=PP/sumpp;%建立概率分布
Pcum(1)=PP(1); 
  for i=2:Len_LJD 
  Pcum(i)=Pcum(i-1)+PP(i); 
  end 
Select=find(Pcum>=rand); 
to_visit=LJD(Select(1)); 
%状态更新和记录
Path=[Path,to_visit];       		 %路径增加
PLkm=PLkm+DD(W,to_visit);    %路径长度增加
W=to_visit;                   %蚂蚁移到下一个节点
   for kk=1:N 
      if TABUkm(kk)==0 
      DD(W,kk)=0; 
      DD(kk,W)=0; 
      end 
   end 
TABUkm(W)=0;				%已访问过的节点从禁忌表中删除
 DW=DD(W,:); 
DW1=find(DW); 
for j=1:length(DW1) 
    if TABUkm(DW1(j))==0 
       DW(j)=0; 
    end 
  end 
LJD=find(DW); 
Len_LJD=length(LJD);%可选节点的个数
 end 
%记下每一代每一只蚂蚁的觅食路线和路线长度
 ROUTES{k,m}=Path; 
   if Path(end)==E 
      PL(k,m)=PLkm; 
      if PLkm<minkl 
          mink=k;minl=m;minkl=PLkm; 
      end 
   else 
      PL(k,m)=0; 
   end 
end 
%更新信息素
Delta_Tau=zeros(N,N);%更新量初始化
   for m=1:M 
     if PL(k,m)  
        ROUT=ROUTES{k,m}; 
        TS=length(ROUT)-1;%跳数
         PL_km=PL(k,m); 
        for s=1:TS 
          x=ROUT(s); 
          y=ROUT(s+1); 
          Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km; 
          Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km; 
        end 
     end 
  end 
Tau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分，新增加一部分
 end 
%绘图
plotif=1;%是否绘图的控制参数
 if plotif==1 %绘收敛曲线
    minPL=zeros(K); 
   for i=1:K 
     PLK=PL(i,:); 
     Nonzero=find(PLK); 
     PLKPLK=PLK(Nonzero); 
     minPL(i)=min(PLKPLK); 
   end 
figure(1) 
plot(minPL); 
hold on 
grid on 
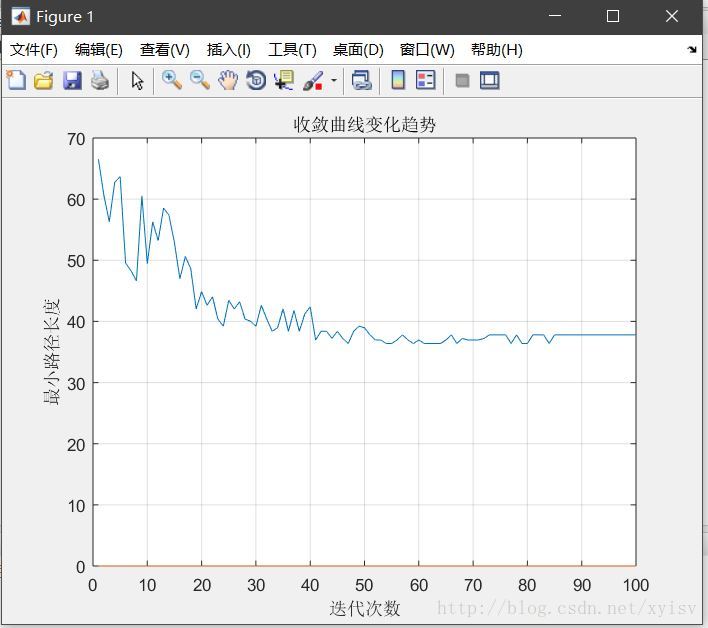
title('收敛曲线变化趋势'); 
xlabel('迭代次数'); 
ylabel('最小路径长度'); %绘爬行图
figure(2) 
axis([0,MM,0,MM]) 
for i=1:MM 
for j=1:MM 
if G(i,j)==1 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); 
hold on 
else 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); 
hold on 
end 
end 
end 
hold on 
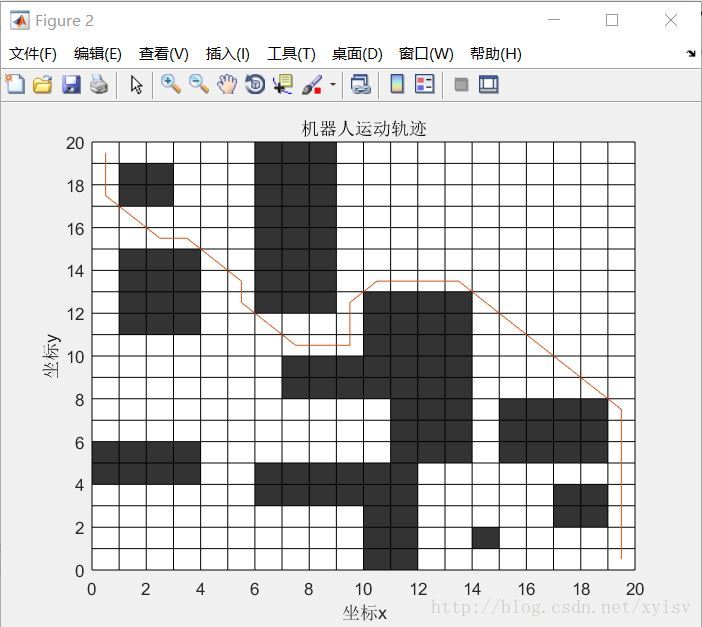
title('机器人运动轨迹'); 
xlabel('坐标x'); 
ylabel('坐标y');
ROUT=ROUTES{mink,minl}; 
LENROUT=length(ROUT); 
Rx=ROUT; 
Ry=ROUT; 
for ii=1:LENROUT 
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5); 
if Rx(ii)==-0.5 
Rx(ii)=MM-0.5; 
end 
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM)); 
end 
plot(Rx,Ry) 
end 
plotif2=0;%绘各代蚂蚁爬行图
if plotif2==1 
figure(3) 
axis([0,MM,0,MM]) 
for i=1:MM 
for j=1:MM 
if G(i,j)==1 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); 
hold on 
else 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); 
hold on 
end 
end 
end 
for k=1:K 
PLK=PL(k,:); 
minPLK=min(PLK); 
pos=find(PLK==minPLK); 
m=pos(1); 
ROUT=ROUTES{k,m}; 
LENROUT=length(ROUT); 
Rx=ROUT; 
Ry=ROUT; 
for ii=1:LENROUT 
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5); 
if Rx(ii)==-0.5 
Rx(ii)=MM-0.5; 
end 
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM)); 
end 
plot(Rx,Ry) 
hold on 
end 
end 
function D=G2D(G) 
l=size(G,1); 
D=zeros(l*l,l*l); 
for i=1:l 
    for j=1:l 
        if G(i,j)==0 
            for m=1:l 
                for n=1:l 
                    if G(m,n)==0 
                        im=abs(i-m);jn=abs(j-n); 
                        if im+jn==1||(im==1&&jn==1) 
                        D((i-1)*l+j,(m-1)*l+n)=(im+jn)^0.5; 
                        end 
                    end 
                end 
            end 
        end 
    end 
end

效果：
这里写图片描述
最短路径长度稳定在38。

G2D及多出口情况参考：http://www.omegaxyz.com/2019/01/28/aco_routes2/

Reacubeth

关注

83
点赞
踩
709

收藏

觉得还不错? 一键收藏
100
评论
蚁群算法（ACO）最短路径规划（MATLAB）

蚁群算法最早是由Marco Dorigo等人在1991年提出，他们在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，据此提出了基于信息正反馈原理的蚁群算法。蚁群算法根据模拟蚂蚁寻找食物的最短路径行为来设计的仿生算法，因此一般而言，蚁群算法用来解决最短路径问题，并真的在旅行商问题（TSP，一个寻找最短路径的问题）上取得了比较好的成效。
复制链接

扫一扫