ddpm数学原理

论文

alpha是自定义的参数。推导以后xt只和x0相关。xt-1和xt相关
推导核心知识点：
最大似然估计、贝叶斯公式、假设高斯分布、KL散度、变分分布、期望、边界估计、近似计算

生成模型底层逻辑

最大似然估计

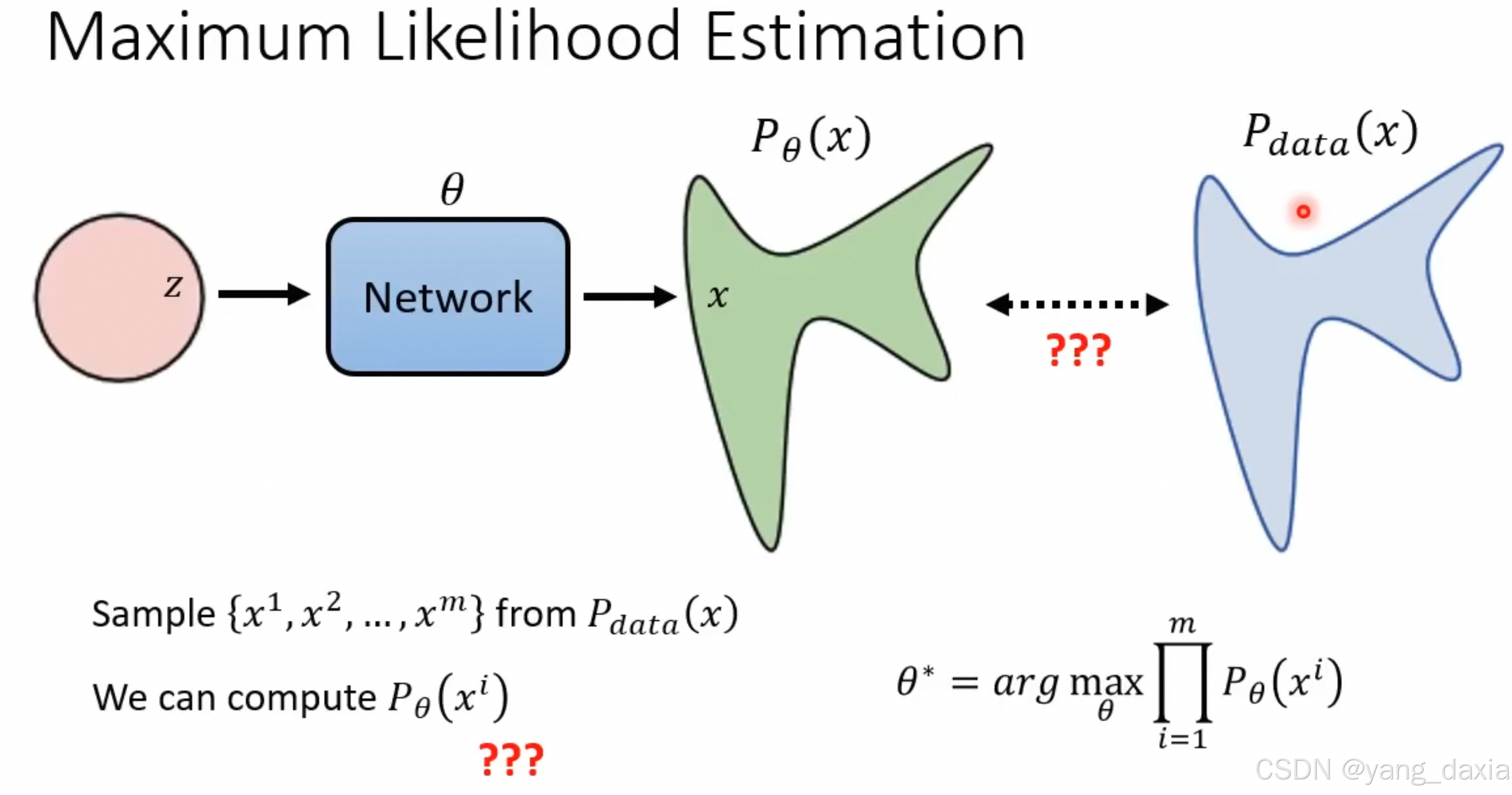
等价于最小化两者的kl散度

约等号是理解为近似为对全体x属于Pdata分布的期望。
后面的减法为了近似计算为kl散度。
P理解成概率、分布

VAE

概率推导

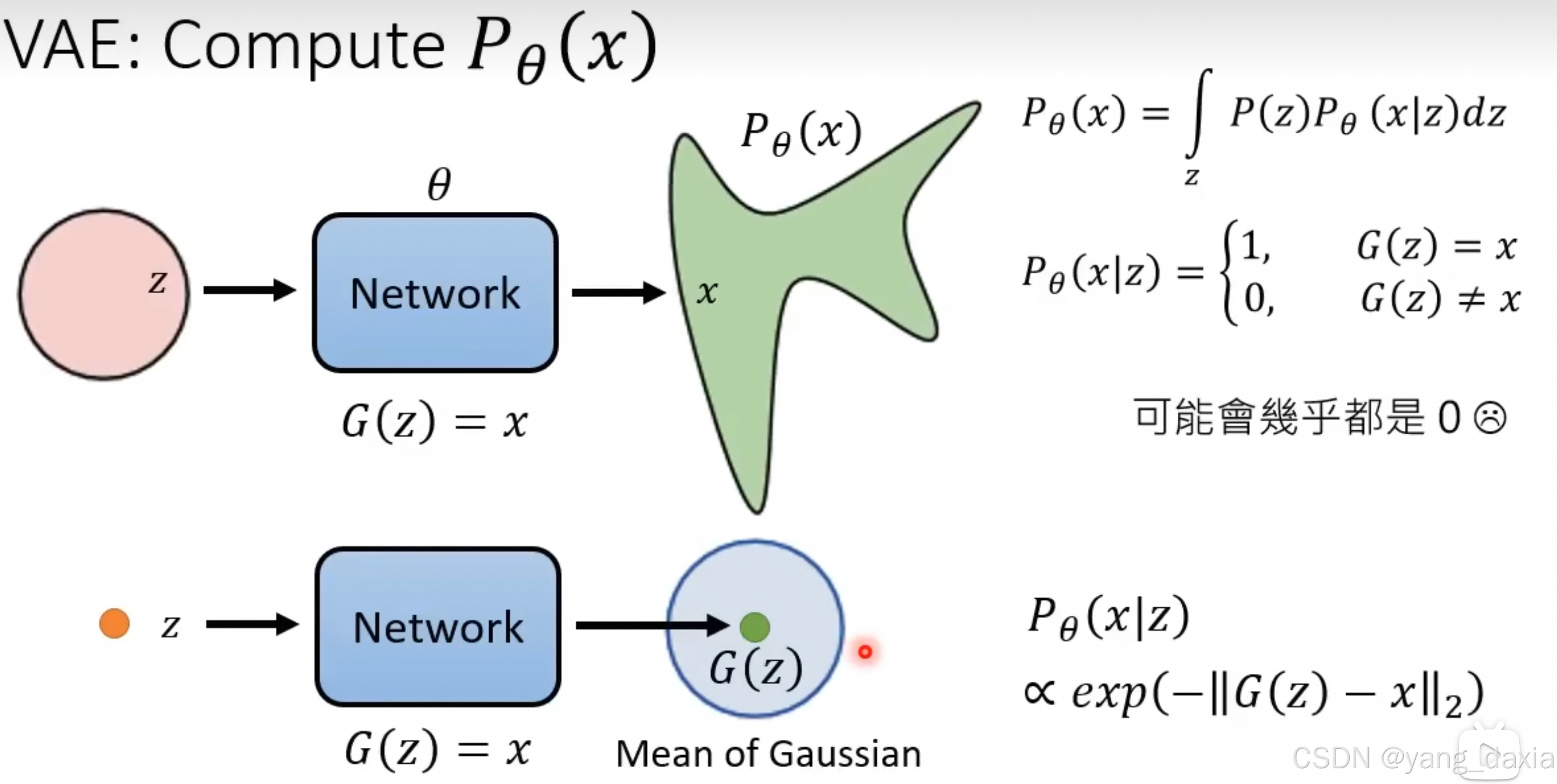
假设生成的p的分布是高斯分布

下界估计（变分推导）

通过变分推理，把最小化kl散度转化为最大化q的期望。
变分推理的核心：用一个分布估计一个没有表达式的分布。后验概率无法求出来。
推导的核心思想是通过引入潜变量 z 和变分分布 q(z∣x)，以及KL散度，来为对数似然函数提供一个可优化的下界。在训练VAE时，我们优化这个下界，进而可以间接优化原始的对数似然函数，这是变分自编码器的一个关键性质

ddpm

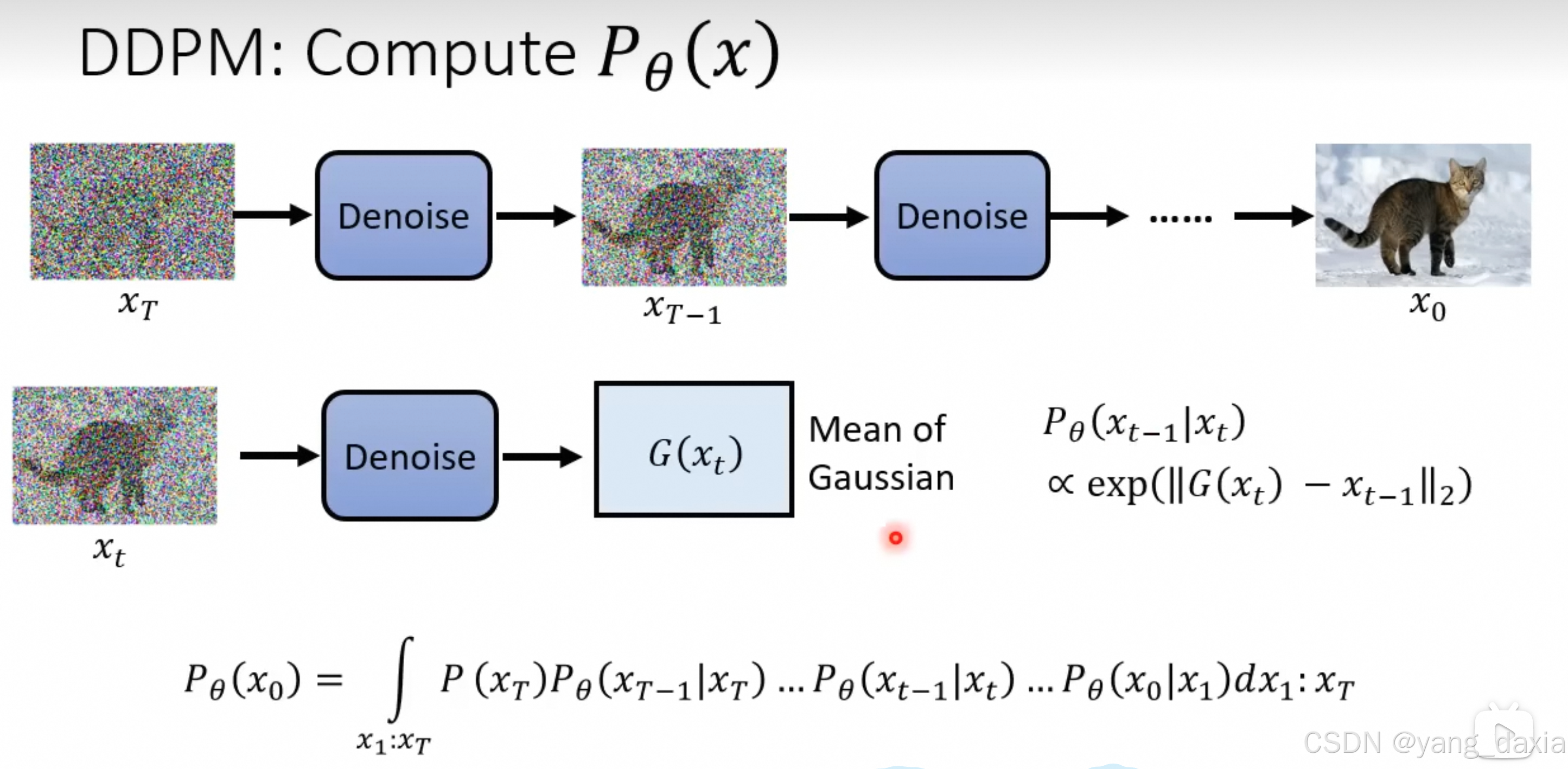
假设diffusion的去噪声模型输出的分布符合高斯分布

diffusion的下界估计和 vae类似

推导

t步操作经过推理后，发现等价于一次操作就行了。

详细推导

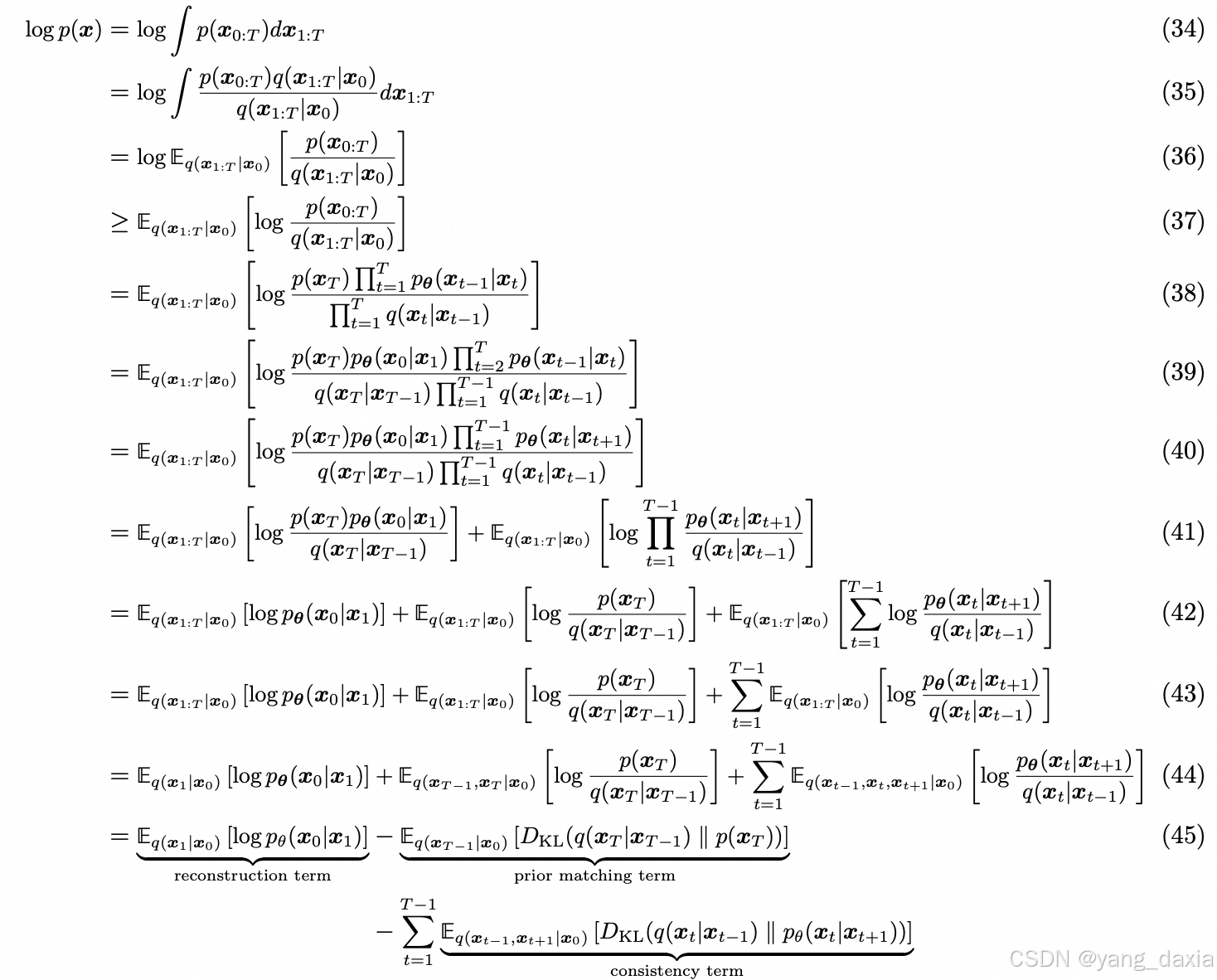
贝叶斯公式推导

发现也是一个正态分布

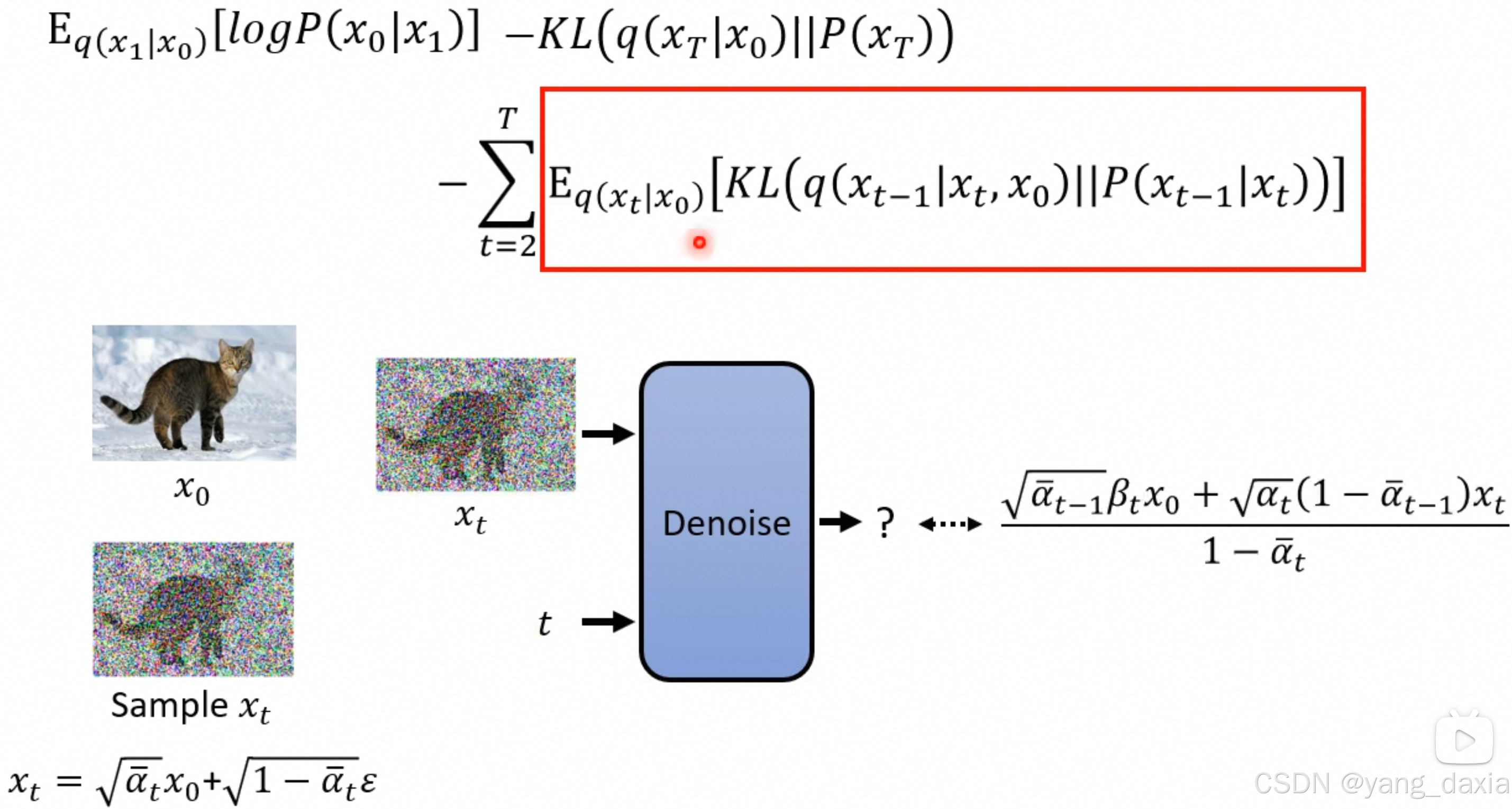
q分布带入进来，发现至于x0和xt相关

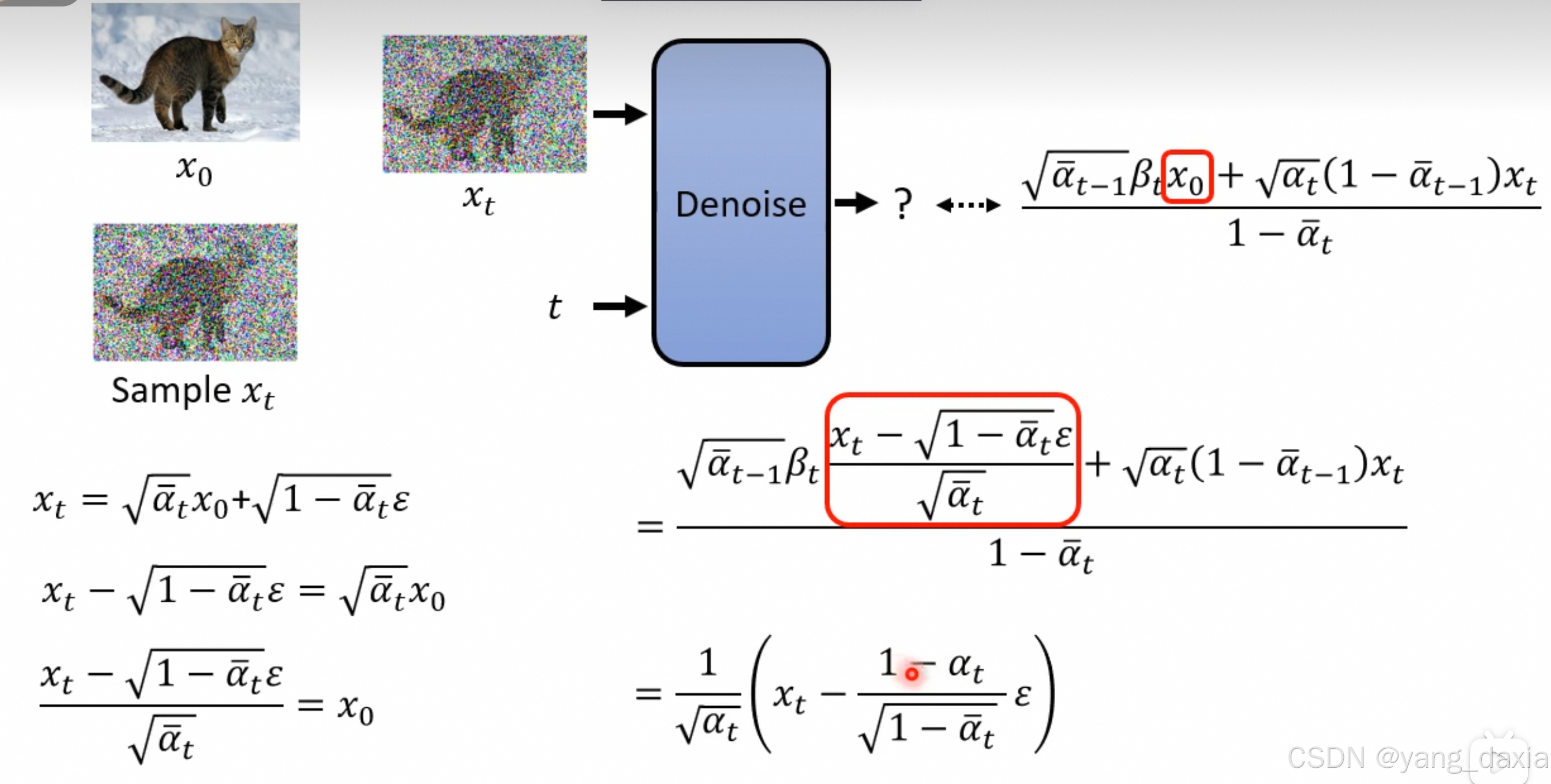
进一步带入x0发现至于xt相关！！！对应论文sampling

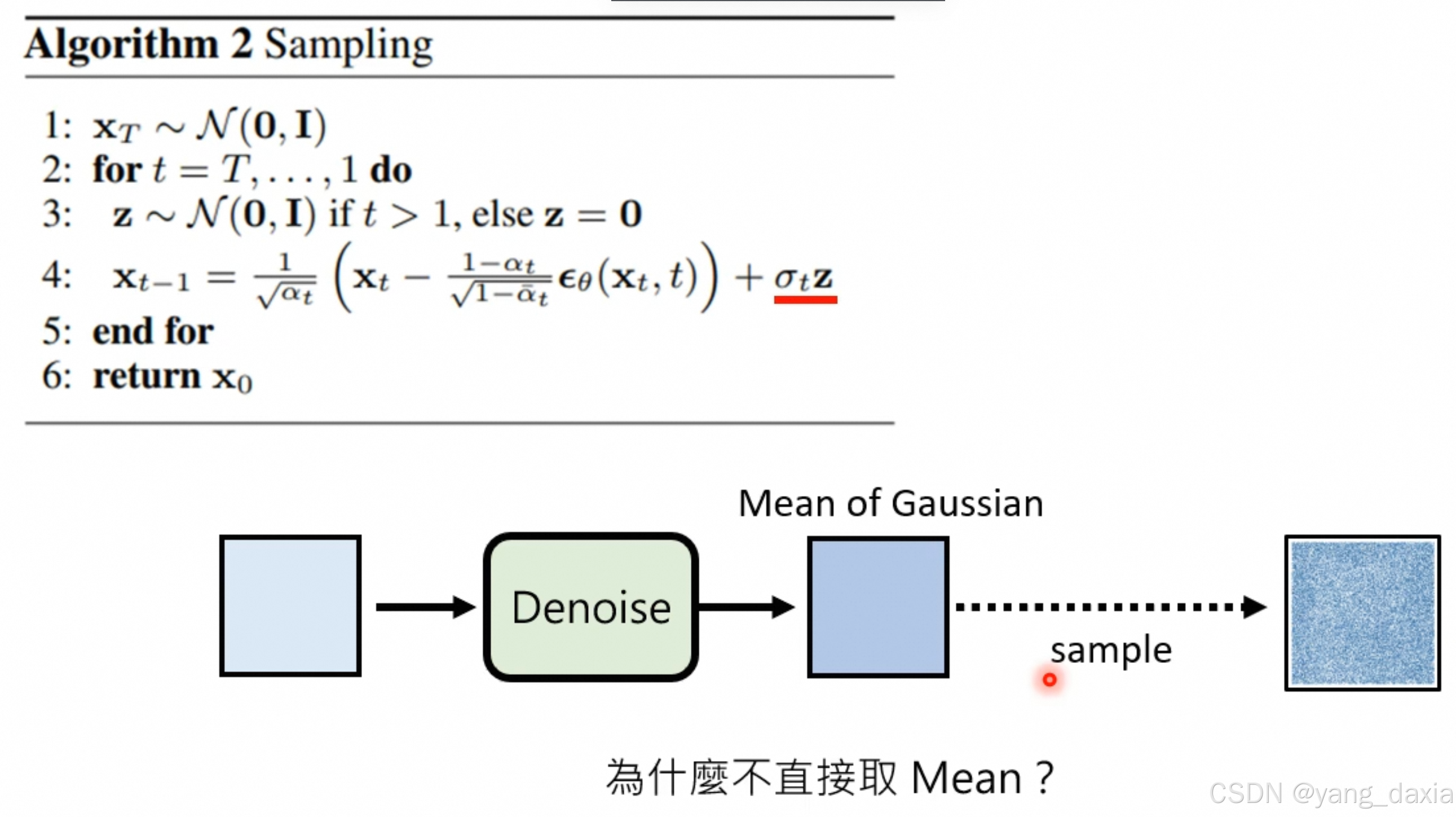
实际上最后又加了一个正态分布：

在生成过程中，每一步我们都尝试去恢复原始数据x 0。然而，因为原始的生成过程包含了随机性（通过噪声的增加），所以在恢复过程中也需要引入相应的随机性来模仿这个噪声。这样，我们就能够遍历所有可能的噪声路径来找到对应于我们想要生成的数据的路径。
类似语言模型中的beam search作用，概率最大的不一定是最好的，使用Random Sample增加随机性

参考：【扩散模型 - Diffusion Model【李宏毅2023】】 https://www.bilibili.com/video/BV14c411J7f2/?p=4&share_source=copy_web&vd_source=a641d5fd36f9ab534df883ec3f1ed48f

苏神：https://kexue.fm/archives/9119

ddpm代码

    
timesteps = 500
beta1 = 1e-4
beat2 = 0.02

b_t = (beat2 - beta1) * torch.linspace(0, 1, timesteps + 1) + beta1
a_t = 1 - b_t
ab_t = torch.cumsum(a_t.log(), dim=0).exp()
ab_t[0] = 1
    
def denoise_add_noise(x, t, pred_noise, z=None):
    if z is None:
        z = torch.randn_like(x)
    noise = b_t.sqrt()[t] * z
    mean = (x - pred_noise *(1 - a_t[t])/(1 - ab_t[t]).sqrt()) / a_t[t].sqrt() 
    return mean + noise

@torch.no_grad()
def sample_ddpm(n_sample, save_rate=20):
    samples = torch.randn(n_sample, 3, height, height).to(device)

    for i in range(timesteps, 0, -1):
        print(i)
        t = torch.tensor([i/timesteps])[:, None, None, None].to(device)

        z = torch.randn_like(samples) if i > 1 else 0
        eps = nn_model(samples, t)
        samples = denoise_add_noise(samples, i, eps, z)
    return samples

参考：https://github.com/Ryota-Kawamura/How-Diffusion-Models-Work

训练代码

# helper function: perturbs an image to a specified noise level
def perturb_input(x, t, noise):
    return ab_t.sqrt()[t, None, None, None] * x + (1 - ab_t[t, None, None, None]) * noise
    
# training without context code

# set into train mode
nn_model.train()

for ep in range(n_epoch):
    print(f'epoch {ep}')
    
    # linearly decay learning rate
    optim.param_groups[0]['lr'] = lrate*(1-ep/n_epoch)
    
    pbar = tqdm(dataloader, mininterval=2 )
    for x, _ in pbar:   # x: images
        optim.zero_grad()
        x = x.to(device)
        
        # perturb data
        noise = torch.randn_like(x)
        t = torch.randint(1, timesteps + 1, (x.shape[0],)).to(device) 
        x_pert = perturb_input(x, t, noise)
        
        # use network to recover noise
        pred_noise = nn_model(x_pert, t / timesteps)
        
        # loss is mean squared error between the predicted and true noise
        loss = F.mse_loss(pred_noise, noise)
        loss.backward()
        
        optim.step()

    # save model periodically
    if ep%4==0 or ep == int(n_epoch-1):
        if not os.path.exists(save_dir):
            os.mkdir(save_dir)
        torch.save(nn_model.state_dict(), save_dir + f"model_{ep}.pth")
        print('saved model at ' + save_dir + f"model_{ep}.pth")