基于非支配排序的多目标小龙虾优化算法求解柔性作业车间调度问题FJSP（MATLAB代码）

基于非支配排序的多目标小龙虾优化算法求解柔性作业车间调度问题FJSP（MATLAB代码）

ID:53170786489389207

智能优化算法MATLAB

基于非支配排序的多目标小龙虾优化算法求解柔性作业车间调度问题FJSP的探讨

概述

在现代制造业中，柔性作业车间调度问题（FJSP）一直是生产管理和调度领域的核心难题。随着技术的发展，多目标优化算法在求解此类问题时得到了广泛应用。本文将介绍一种基于非支配排序的多目标小龙虾优化算法（简称小龙虾算法），及其在求解FJSP中的应用。

一、柔性作业车间调度问题FJSP简介

柔性作业车间调度问题是一类复杂的组合优化问题，涉及多个作业车间的生产调度。其核心目标是实现生产过程的优化，包括提高生产效率、降低生产成本、保证交货期等。由于问题的复杂性，传统的优化方法往往难以得到满意解，因此，多目标优化算法的应用成为了研究的热点。

二、非支配排序算法简述

非支配排序算法是一种常用于多目标优化问题的算法，它通过评估解之间的支配关系，将解分为不同的前沿层，从而找到一组均衡解。该算法在多目标优化问题中表现出良好的性能，尤其适用于求解复杂、高维度的多目标优化问题。

三、小龙虾优化算法介绍

小龙虾优化算法是一种新兴的启发式优化算法，模拟了自然界中小龙虾的觅食行为。该算法具有较强的全局搜索能力和优化性能，适用于求解复杂的优化问题。在结合非支配排序的基础上，小龙虾算法能够在多目标优化问题中寻找到一组均衡解，满足不同的优化目标。

四、基于非支配排序的小龙虾算法在FJSP中的应用

针对FJSP问题，结合非支配排序的小龙虾优化算法能够通过迭代搜索，找到一组均衡的生产调度方案。该算法首先根据FJSP的问题特点，构建适应度函数，评估各生产方案的优劣。然后，通过小龙虾算法的全局搜索能力，寻找一组满足多个优化目标的调度方案。最后，利用非支配排序的思想，对找到的调度方案进行排序和筛选，得到最终的调度结果。该算法不仅能提高生产效率，还能在生产成本、交货期等多个目标之间实现均衡。

五、实验结果与分析

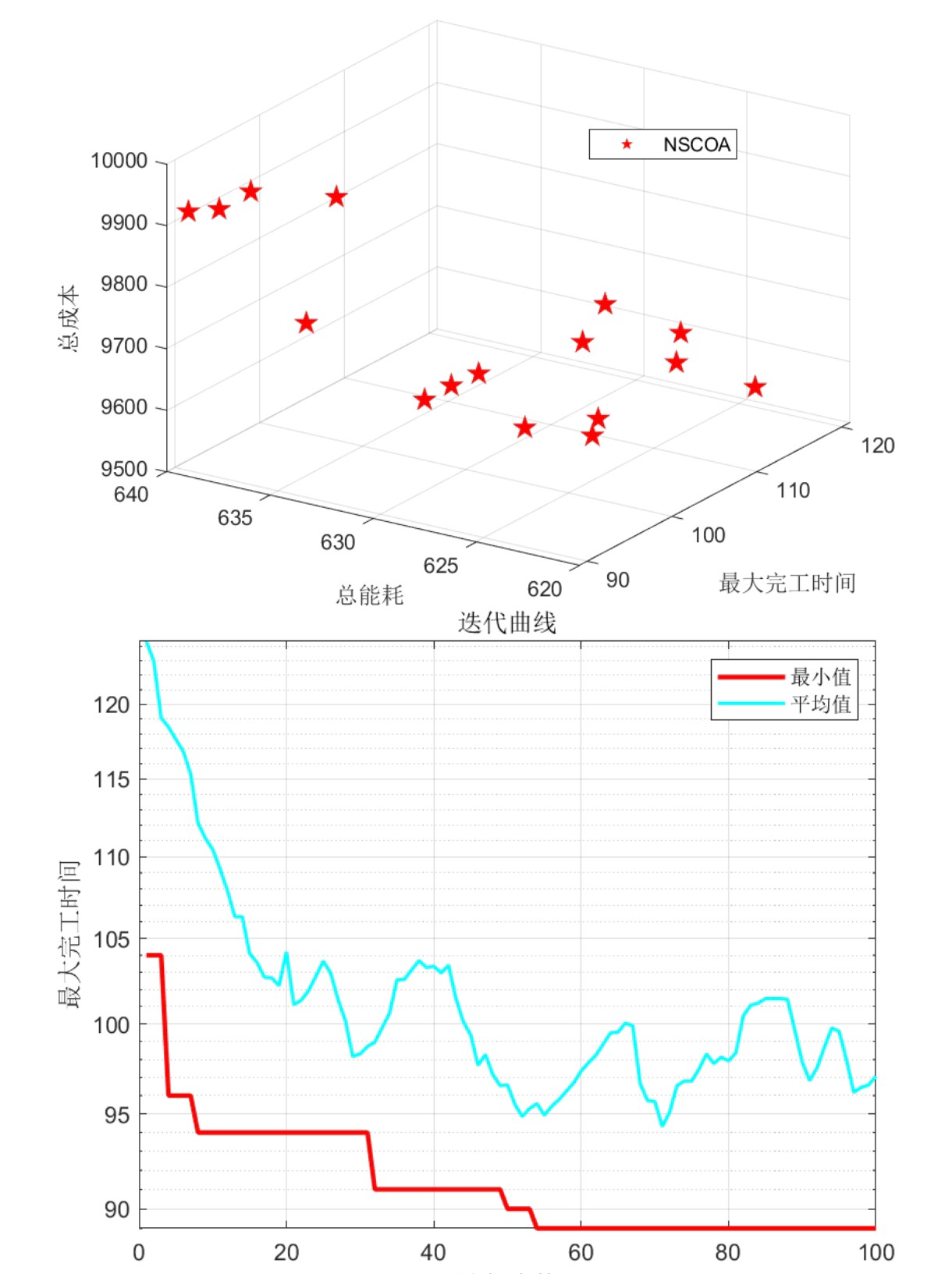
为了验证小龙虾算法在求解FJSP问题中的有效性，我们进行了大量的实验。实验结果表明，该算法能够找到一组均衡的调度方案，满足多个优化目标的要求。与传统的优化方法相比，小龙虾算法具有更好的全局搜索能力和优化性能。此外，该算法还具有较强的鲁棒性，能够在不同的实验条件下保持较好的性能。

六、结论与展望

本文介绍了基于非支配排序的小龙虾优化算法在求解柔性作业车间调度问题FJSP中的应用。实验结果表明，该算法能够有效地解决FJSP问题，实现生产过程的优化。未来，我们将进一步研究小龙虾算法在其他优化问题中的应用，并探索算法的改进和优化方向，以提高算法的效率和性能。同时，我们还将研究如何将小龙虾算法与其他智能优化算法相结合，以更好地解决复杂的优化问题。总之，基于非支配排序的小龙虾优化算法在求解FJSP问题中具有良好的应用前景和研究价值。

相关的代码,程序地址如下：http://matup.cn/786489389207.html