[yzhpdh多读paper]Social network analysis:An overview

以下为本人在阅读文章中记录的对自身有启发的内容，按照文章发表的顺序记录
Social network analysis也叫SNA,它提出的目的是研究社会角色在社交网络中交互的形式，所以其强调的是关系而不是个体本身。
除此之外，SNA还包括挖掘网络中重要角色的任务，在公司中有以下应用：

1. 一些公司可以使用瞄准具有更高网络价值的客户来最大优化他们产品的口碑。
2. 在移动电信部门运营的公司，将SNA技术应用于电话网络，并使用它们来识别客户的配置文件，并根据这些配置文件推荐个性化的移动电话收费。
3. 使用SNA进行客户流失预测，也就是说，通过检测电话联系模式的变化来检测那些可能切换到其他移动运营商的客户。
4. 欺诈检测，有公司通过分析正式邮件与非正式邮件的频率和方向来识别员工和管理者的关系，这样可以帮助识别那些参与欺诈活动的个体。
   总之以上内容表明近几年将SNA应用于实际生活中的问题与不同网络的研究十分火热，
   Some examples of two-mode networks（有两个点集合的网络） include user–product networks (Amazon, eBay, etc.), membership or affiliation networks (actor–movies (IMDB), user–group (youtube), user–
   channel (youtube), user–project (GitHub), user–organization, etc.), user–preference networks (Pinterest, Instagram, Twitter),
   citation networks, user–stock investment.
   
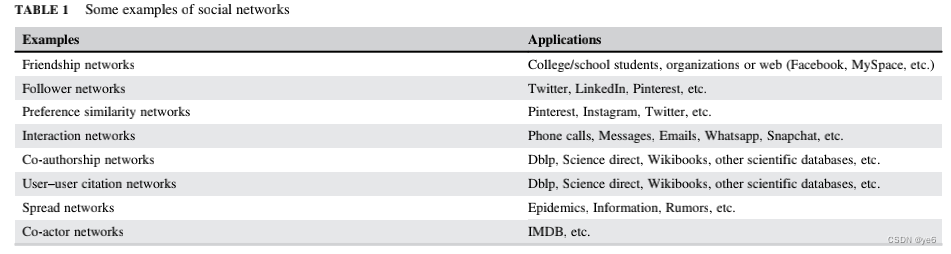
   第二节，文章分别从node-level与network-level来介绍一些图论的知识。在node-level上，探索了中心性的一般度量，作为一种理解顶点在图的整体结构中的位置的方法，因此，有助于识别网络中的关键参与者。network-level提供了更紧凑的信息，并允许评估网络的整体结构，从而洞察潜在社会现象的重要属性

Node-level statistical measures

需要说明的是对于这些提出metrics，在对不同网络计算出的结果进行比较前需要对它们各自的结果进行正则化。
Degree or valency
度数，这个概念比较简单就不赘述了，对于无向图就是直接与其相连的点的个数，对于有向图，就分为入度（支持度）出度（影响力）
Barabási and Albert (1999) and Barabási andBonabeau (2003)发现大多数真实网络遵循幂律分布，至少是渐近的。这意味着，在这些网络中，顶点的度数分布非常不均匀，并且高度右倾斜，绝大多数顶点度数较低，少数顶点度数较高。
Betweenness
节点间度b衡量一个节点位于网络中其他节点之间的程度，可以用经过该节点的最短路径的百分比来计算。一般这个指标较好的节点可以认为是这个网络中的信息传播节点，.这些联系对于寻求获取新信息和资源的个人来说是很有意义的，因为它们使社区信息的传播更容易。以下是该指标的一般算法，即点s与点t之间的经过v的最短路径/点s与点t之间的最短路径

然而，这样的情况在现实世界中是非常罕见的，即使它们发生了，由于这些边的不稳定，它们所带来的优势通常是暂时的。一个比较常见和现实的情况是本地桥梁。式(6)表示了该测度的计算方法:即点u与点v之间经过边e的最短路径与点u与点v之间最短路径相除的和

Closeness
这是对一个节点到达其他节点距离的粗略估计，一般是该节点作为起点到其他各个节点的最短路径的平均。由于它的定义，这个度量通常只计算最大组件组件内的节点。可达性的衡量标准，它衡量给定的参与者能够多快地到达网络中的每个人。
Eigenvector centrality
特征向量中心性。简单来说就是给定节点i的中心性与i的邻居的中心性之和是相关的。
特征向量中心性是程度的一个更复杂的版本，它假设不是所有的连接都具有相同的重要性，不仅考虑到这些连接的数量，而且尤其考虑到这些连接的质量。

上面𝛌代表邻接矩阵最大的特征值，aij代表点i,j是否连通。xi,xj分别代表点i,j的中心性
Local clustering coefficient

Ni是Vi的邻居， |ejk|表示节点vi的领居节点之间有几条直接相连边。Ki是Vi的度数。其实这个式子可以看成：节点vi的领居节点直接相连边数/（节点vi的领居两两相连的数量，即ki*(ki-1)/2）

Network-level statistical measures

geodesic distance:也叫最短距离
eccentricity：离心率,即给定节点vi，在网络中与其最远节点的最短距离。

Diameter and radius（直径和半径）
前者表示网络中两个节点最长的最短距离，后者表示网络中两个节点最短的最短距离。一般来说，稀疏矩阵比稠密矩阵的直径更长，在现实网络中，有效直径会随时间缩短，这与传统的增加直径的想法相反。

Average geodesic distance
这个指标一般被用于衡量信息在网络中流通的效率当网络中不止一个连通分量时，且某个联通分量中只有1个节点，那么上面这个式子就不合适了，所以采用下面这个公式，即采用 harmonic average geodesic distance（调和级数测量距离）

Average degree
就是网络中所有节点度数的平均值。这个可以用于衡量全局连接性。

Reciprocity（互惠、互换）
这个一般用于衡量有向图中两个点之间相连的倾向。比较流行的计算方法是#mut（两个节点之间相互连接的情况），#asym(两个节点之间只有一个节点与另外一个节点相连的情况）

Density
这可以解释网络中一般程度的连通性。这个变量比较好理解，就是这个图中的边数/这个图最大边数（对于无向图时是n*(n-1)/2,对于有向图是n*(n-1)
Global clustering coefficient(全局聚类系数）
即局部的聚类系数的平均值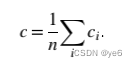

(留一个问题就是：什么时候计算局部聚类系数，什么时候计算全局聚类系数呢？
我通过查找资料给出的认识是全局聚类系数可用于比较不同网络之间的连通性，局部聚类系数针对某个点周围）

EGO NETWORKS

ego network是一个特定节点的局部网络。ego就是某个焦点节点，而与其连接的节点称为 alters。这种网络映射了ego与alters之间的关系。与ego直接相连的alters称为primary alters,隔一个alter相连的称为secondary alter.且研究表明局部ego betweenness与该点在整个网络的betweenness呈强相关关系

ego networks analysis
分析ego networks不仅可以洞察整个网络，而且可以在记忆受限的情况下广泛利用。通过分析社交网络的ego networks并对其进行独立计算，可以解决重要的图挖掘任务.基于ego network的指标，虽然是网络层面的测量，但它们是专门针对个人网络中的ego(节点层面)的属性/特征而设计的，而不是alters的。
在介绍这些指标前，首先要了解两个概念：
redudant path:当网络中两个节点之间存在多条路径时，我们称之为冗余路径。
structural hole:非冗余触点之间的分离/连接。它也可以是连接到不同集群的两个节点之间的桥梁。
Number of components（子图数量）
在有向图中，若忽视边的方向，存在至少一条路径使得所有点可以相互连接，这种被称为弱连接，反之不忽视边方向，所有点都互相连接，则被称为强连接。
ego周围的子图越多(大)，ego就被认为在通过单一点到达许多群体(例如:传播信息或病毒)方面更重要。
Effective size
有效规模的衡量体现了ego对alters的控制，或投资于alters的每一个单位所获得的利益。
当ego旁的alters相互之间强连接，那ego从中得到的好处是有限的，周围的强连接也是冗余的。而当不同alters连接到各自的次要网络时就会使得信息在非冗余网络中最大化。
在像社交网络这样的稀疏网络中(密度≈0)，网络的有效规模随着alters数的增加而增加，而在密集网络中，它保持不变。因此，当稀疏网络中alters数增加时，我们可以假定有效大小也在增加。有效大小的最大限制等于网络中的alters数
目前它的计算方法如下：n为ego network中alters数，t为ego network中连接总数

Efficiency
这其实是effective size的归一化表示，就是在es的基础上除以alters总数。
聚类系数高的ego networks的efficiency较低。efficiency比较适合不同ego networks进行benefit情况的比较
yzhpdh:但这是2018年的论文，确实是在SNA非常火热的时候，但最近根据搜集到的数据，这个热潮也许有点下来了…?
Constraint
Constraint与冗余类似，在有效尺寸的测量方面，由于它还考虑了网络中每个alters周围的structural holes.如果网络更冗余，structural holes更少，那么ego就会更constraint。一个ego的constraint是在ego network中所有alters的constraint的总和。每个alter对ego的constraint(Cej)取决于alter与ego和网络中所有其他altersPej的关系的比例，以及与网络中其他alters Pqj的关系的总和，以及它们与ego,Peq的关系的总和。如下式所示:

在自己的一端没有结构空洞而在另一端有丰富结构空洞的关系的玩家/自我在结构上是自主的，并且处于他所认为的信息和控制利益的有利位置。

Krackhardt efficiency
它是一个图的多个分量或一个有向图的多个弱分量中不冗余的度量。如果我们认为ego network是一个层次结构，ego是根，利用该度量方法计算边的不冗余度。且efficiency与密度成反比

LINK ANALYSIS

在类似于web这类网络中，人们往往希望能获得最有价值、最具备影响力、最权威的一组页面，因此出现了以下几种算法：HITS29 、 Brin 、Page。这些算法探索了链接之间的关系，以及web界面的内容。
Hubs and authorities
hubs是某个特定主题的网页汇编。一个hub的质量取决于它所指向的权威机构的质量决定。另一方面，权威是被许多不同hubs引用的网页，这意味着它们的相关性是由它们收到的内部链接的数量来衡量的。一般来说，高权威的界面中的内容是对于某个主题的可靠信息来源。
PageRank algorithm
简单来说，这个算法根据一个网页被链接的数量与质量来衡量这个网页的重要程度
简述一下算法实现流程：
1.初始化网络。给网络中每个节点分配一个page rank value为1/n.并且确定该算法的迭代次数
2.将节点p的实际PageRank值除以其输出链接数，并将这些相等的份额传递给其指向的节点。注意，如果节点p没有传出链接，PageRank共享将传递给自身。节点的PageRank值的更新是通过将它在每次迭代中接收到的共享相加来执行的。应用该规则直到第k次迭代，或者直到收敛。
Link prediction
链路预测问题也可以解释为在给定网络当前状态的情况下，预测哪些链路在未来更有可能出现的问题。Temporal link prediction时间链路预测是指时间演化网络中的链路预测问题，网络中有多个snapshots(快照)可用。比如给定1-n个快照，预测第n+1个快照中哪条链路会出现。
时间链接预测的问题已经通过考虑时间不可知(其中时间信息没有被利用)和时间感知方法(其中时间信息被合并)得到解决。
在时间不可知的方法中，最常见的方法是对所有网络时间戳进行折叠，并应用为静态环境设计的传统方法对折叠结果进行折叠。
传统的方法是计算每对网络节点之间的相似度得分，得分越高表示相似度越高。得分一般是该节点的邻居数或者节点之间的路径数来定义。
还有一些研究者考虑了分类的方法。这些方法的思想是利用一组网络特征来训练分类器，并进一步用于预测未来的链接。两部作品都使用了逻辑回归，除此之外，作者除了考虑拓扑和语义特征外，还考虑了共现概率。
对于时间感知方法，最常见的方法是考虑基于时间序列的方法。这种方法的思想是利用网络在给定时刻的状态来构造时间序列，并对其进行进一步的预测。
还有Dunlavy, Kolda, and Acar (2011) and Spiegel, Clausen, Albayrak, and Kunegis (2011)的工作将时间演进的网络作为一个张量进行建模，采用张量分解技术，结合预测模型估计该张量未来的时间片，对应网络未来的状态。
Bringmann, Berlingerio, Bonchi和Gionis(2010)和Juszczyszyn, Musial和Budka(2011)提出了基于进化模式挖掘的方法。
COMMUNITY DETECTION
社区可以认为是许多个节点之间连接密集，且不同社区之间边不密集。这些连接可以是有向的也可以是无向的。
在网络数据中发现社区的研究主要有两条主线：
第一种方法起源于计算机科学，被称为图划分。它的提出起源于如何更好的将任务分配给处理器以最少化它们之间的交流，主要是在并行计算环境中提高计算。
第二种主要是由社会学家提出的，通常被称为块建模，分层聚类或社区结构检测。其动机是寻找社会中社区小组，从而简化将人按照相似性进行排列的对社会现象的分析。

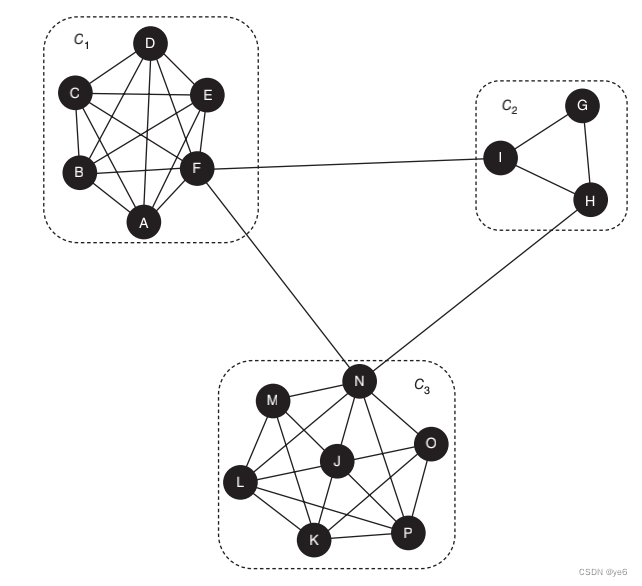
下面几节将介绍最流行的(不一定是最好的)方法来解决查找社区的问题。这些传统算法中绝大多数采用了对顶点的划分，而不是覆盖(Moreno, 1934)，也就是说，它们不允许社区重叠，所以每个顶点被分配到一个单一的社区。但假如某个节点就是处于两个社区的交集处，那么也可以使用 Clique Percolation Method(CPM)，由物理学家 Palla, Derényi, Farkas and Vicsek (2005)提出。对于那些有兴趣使用CPM来检测重叠社区的人，Palla和他的同事们开发了CFinder软件包，可以在www.cfinder.org上免费获得。
Hierarchical clustering（分层聚类）
分层集群是查找集群的一种流行方法，因为它不需要对集群的数量、成员关系和大小进行任何假设。分层聚类算法产生一种灵活的嵌套结构(更小的集群中更大的集群，反过来，嵌入更大的集群)，通常通过树状图表示，揭示了网络的多层次结构。这样的特性在关于网络的社区结构的信息很少的领域是非常需要的。
传统的层次聚类过程非常直观，强烈地基于相似度的定义。通常，第一步是根据给定的全局或局部属性选择用于评估两个对象相似程度的相似度量。这类度量的例子有余弦相似度、Jaccard指数、欧几里得距离或曼哈顿距离、汉明距离等。下一步是计算所有对象对之间的相似性矩阵。然后，选择将它们分组的方法，分裂或聚合方法，选择一个给定的距离度量来计算集群之间的相似性(例如，单链接、完全链接、沃德方法等)。结果是一个树状图，说明了由层次算法返回的簇的排列。
•分裂方法:这类方法专注于识别和移除密集连接区域之间的跨越链接(Easley & Kleinberg, 2010)，即桥梁和本地桥梁。探讨这种方法的一个著名算法是由Girvan和Newman(2002)提出的。
•聚合方法:这类方法专注于网络中紧密连接的部分，而不是它们边界上的连接。Walktrap (Pons & Latapy, 2005)就是基于这种方法的算法的一个例子。
为了选择最佳分区，即社团的最佳数量k，典型的策略是对每个可能的簇数计算模块化值(Newman, 2003)，并选择使该函数最大化的数。
最后，值得注意的是，社区通常有一个等级结构(Porter, Onnela， & Mucha, 2009)。例如，在一个特定的个人的友谊ego network中，我们可能会发现一个大的社区对应于一个人在他的家乡相遇的人。然后，在这些人中，我们可以找到更小的社区，如他的家人或他的学校同事。以一种分层的方式探索社区结构，可以捕捉到这样不同的层次社区的同质性。

Girvan–Newman algorithm
在解决社群检测问题的算法中，这个可能是最流行的，由 Girvan and Newman在2002年发明。这是一个可分裂的层次技术，将最初的完整网络分解成逐渐小的连接块，直到没有边可以移除，每个节点代表自己的一个社区。他们提出的去除边的准则是用图论中心性度量edge betweenness。这个选择背后的原因与这样一个事实有关，这个中心性度量能够识别位于节点之间的大量最短路径上的边，因此，被认为连接不同的非重叠社区。因此，该算法的主要思想是，如果我们识别并移除桥，我们就隔离了网络中现有的社区。
这个算法适用于有上千个节点的网络，所以计算量比较大。其输入是一整张图。输出是一个层次结构，例如树形图，其中任意层次的社区对应于这个层次树的水平切割。这个算法的大致步骤如下：

1. 计算网络中所有边的betweenness;
2. 去掉betweenness最高的边。这一步可能会导致网络分裂成独立的不连接的部分，这些部分构成了图划分中的第一级区域。
3. 重复前面的步骤，直到图中没有要移除的边为止。请注意，在较大子图中获得的较小子图是嵌套在第一步中找到的较大区域中的区域。由于它的流行，几乎所有的标准软件库都实现了这个算法。例如，在R (Ihaka & Gentleman, 1996)中，我们可以使用library igraph提供的edge.between .community函数来应用Girvan-Newman算法。

Modularity optimization（模块化优化）
指标模块化Q是一个衡量网络划分质量的函数，也可以作为目标函数进行优化。同时可以推断模块化是一个明确考虑到边缘异质性（指一些事物在某些特征上存在差异）的度量。其基本思想是，在随机选择的基础上，如果社区之间的边数量少于预期，网络就会显示出有意义的社区结构。

m是边数，ki、kj分别代表节点i与节点j的度数，Aij代表邻接矩阵中ij之间的边数，kikj/2m表示落在这些节点之间的边的期望数量，ci和cj表示节点i和j所属的组，δ(ci, cj)表示Kronecker delta（即克罗内克函数，δij是一个二元函数，克罗内克函数的自变量（输入值）一般是两个整数，如果两者相等，则其输出值为1，否则为0。）
从公式中，我们可以推断出Q 属于[−1,1]，不是负的就是正的。如果是正的，那么就有可能在网络上找到社区结构。如果Q不仅是正的，而且很大，那么相应的划分可能反映真实的社区结构。根据克劳塞特，纽曼和摩尔(2004)，在实践中发现，modularity约为0.3是有意义社区存在的一个很好的标志。
由之前的工作可知modularity越高，代表对网络的划分越好。但由于通过暴力寻找划分答案是粉低效耗时，所以一些研究者提出方法去解决这个问题。
一种是由Blondel, Guillaume, lambitte和Lefebvre(2008)提出的，通过探索贪婪技术对模块化进行层次优化，另一种是由Guimera和Amaral(2005)提出的，将模拟退火程序应用于模块化优化问题。那些有兴趣了解更多关于在网络中寻找社区问题的人，可以参考Fortunato(2010)最近发布的调查。
EVOLVING NETWORKS
网络的节点和链接的数量/行为/特征随着时间的变化而变化，这被称为演变网络。
以往的研究发现现实世界数据网络遵循幂律分布，原因是节点的优先连接，也就是说，新节点优先连接到已经连接良好的节点。Dorogovtsev and Mendes(2001)证明了不同的优先连接会产生不同类型的无标度网络（符合幂律分布）。 Reed and Jorgensen (2004)证明了如果一个随机过程呈指数增长，并且被观察到一次“随机”，观察状态的分布将在一个或两个尾部遵循幂律。

Newman(2001)验证了先前的理论，即在增长的网络中存在集群和偏好依恋。他以经验证明，两个节点之间的链接的概率与相互认识熟人/邻居的数量呈指数级强正相关，而与之前的链接的数量呈线性相关。

进一步，Barabâsi等人(2002)分析了非常稀疏的共同作者网络(比如聚集了大约70k个节点和70k条边)在更小的时间步长的拓扑属性(与上述参考文献相比)。从1年到7年。基于他们的经验测量，作者发现这些网络工作的平均程度随时间增加，节点分离减少。此外，他们还发现这些网络的聚类系数随着时间的推移而衰减，而最大簇的相对大小则增加。
Temporal networks
这里比较有意思的是将现实生活的不同场景建模成图，赋予边或点不同的含义。比如以下两张图

第一张图边上的数字代表A、B在t=3,6,11时刻交互。第二张图代表A在11时刻followB,在12时刻unfollow
词汇积累：
resorting to：求助于
eigenvector centrality：特征向量中心性
betweenness：中间性
spectral graph theory：谱图理论
focal：焦点的
transitivity：传递性
normalize：正则化
metric:衡量指标
valency：价
denote：表示
immediate adjacency：直接邻接
incident：入射的
prestige：声望、威信
asymptotically:渐进的
right-skewed:右偏态的
scale-free:无标度的
coin by:由什么创造
exponential：指数的
extent：程度、长度、范围
pass through:通过
tightly-knit ：紧密团结的
gatekeeper:信息传递者
confer：授予、赋予
eigenvector：特征向量
egocentric：自我中心的
elaborated:详尽的
fraction:分数、部分
geodesic:测量的
eccentricity:离心率
namely：即，也就是
proximity:靠近（时间、空间）
nullifying：使无效
harmonic：调和级数的
clique ：小圈子
focal：焦点的
pertinent:切题的、相关的
whereas:然而
constant：恒定的、不变的、持续不断的
applicability:适用性
delineate：描绘
information retrieval：信息检索
compilation：汇编、编纂
inward：内向的
overtake：追上、赶上
temporal：时间的、暂时的
tackle：解决
clique：派系、小圈子
metabolic：新陈代谢的
intermediate：中间的
coarse-grained：粗糙的
overlap:重叠、交叠
percolation ：过滤、浸透
dendrogram：系统树图
agglomerative：会凝聚的
divisive:分离的
devise:设计、发明
albeit：尽管
intractable：棘手的
circumvent:规避、克服
heuristic：启发式的
simulated annealing：模拟退火
indicator：标志、迹象
synthetic：人造的、合成的
anomaly：异常事物、反常现象
regularity：规律
stochastic：随机的、猜测的
asymptotically：渐进地
contagion：传染病