基于不确定性梯度匹配的模型合并

23年10月德国Darmstadt大学、日本RIKEN和英国爱丁堡大学的论文“model merging by uncertainty-based gradient matching ”。

在不同数据集上训练的模型可以通过参数的加权平均来合并，但它为什么有效以及何时会失败？ 本文将加权平均的不确定性与梯度的不匹配联系起来，并提出了一种新的基于不确定性的方案，这样减少不匹配来提高性能。 这种联系还揭示了其他方案中的隐含假设，例如平均、任务算术（task arithmetic）和Fisher加权平均。

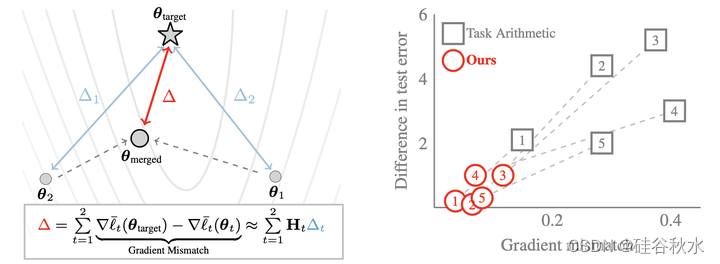
如图所示：左边说明了该模型合并方法。 将合并模型的误差与损失的梯度失配联系起来，并提出一种 Hessian 矩阵和各个模型误差来减少失配的新方法。 右边显示了将数据集添加到在 IMDB 训练的 RoBERTa （BERT预训练方法https://arxiv.org/abs/1907.11692）的示例。 减少不匹配也减少了任务算术的测试错误。 考虑 5 个数据集，每个数据集都用标记上的数字表示。

模型合并中简单的加权-平均公式：

算术-平均和加权版公式如下：

Fisher-平均公式如下：

类似地，可以考虑LLM的Fisher矩阵F0对应的S0。在实践中，为了降低计算成本，可能只用在线方式估计的Fisher对角线（Matena＆Raffel，2022）。 这类似于持续学习的策略（Kirkpatrick，2017），其中Fisher的选择是通过贝叶斯更新 （Husza ́r2018）来证明合理的。 然而，这种连接尚未被用来模型合并。

使用Fisher应该会有所改善，但改善的程度尚不清楚。 Jin 最近的一项工作（2023）使用线性模型证明其中一些选择的合理性，但这种理由可能不适用于非线性模型。 一般来说，也不清楚Fisher-平均如何处理 LLM 模型向量微调 结果之间的共性。 是否应该包含矩阵F0？它应该如何与其他矩阵Ft结合以避免模型中信息的重复计算？ 目前的做法是简单地在验证集上调整
𝛼t，这是弥补错误的一种方法，但随着 T 的增加，这很快就会变得昂贵。

Ilharco（2023）建议用以下简单的“任务算术”（TA）减去 LLM参数向量的贡献：

Daheim (2023)的方法建议：

其中

几个问题：（1）如何选择缩放矩阵； （2）这些选择对合并模型的准确性有何影响； （3）如何获得一种新方法来减少以前方法中的不准确性。 本文提出一种与梯度失配的新联系以及受其启发的新方法来回答这些问题。

为了理解参数平均的不准确性，引入目标模型的概念：即模型合并方法想要估计的模型。 举一个例子：考虑分别在两个数据集 D1 和 D2 上训练的两个模型 θ1 和 θ2如下

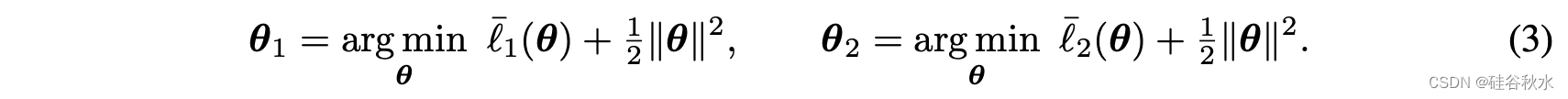
这里，D1 和 D2 的损失函数分别用 l1 (θ) 和 l2 (θ) 表示，正则化器是 L2 正则化器（以下内容也适用于其他显式正则化器，也适用于隐式正则化器）。 本例中的目标模型可以是在两个数据集上联合训练的模型：

用标量 𝛼1 和 𝛼2 反映每个损失函数的相对权重。 现在将梯度失配与目标参数向量和参数平均之间的误差联系起来。 该方法是通用的，适用于不同类型的目标和平均值。

从（3）-（4）方程中模型的一阶平稳条件开始：

然后将第三个方程的结果减去，得到以下表达式：

该表达式表明，如果各个模型已经接近目标模型（就其梯度而言），则参数平均应该相当准确。 它说明还有改进的空间，减少失配可能会带来更好的方案。

考虑在一个大数据训练的LLM模型：

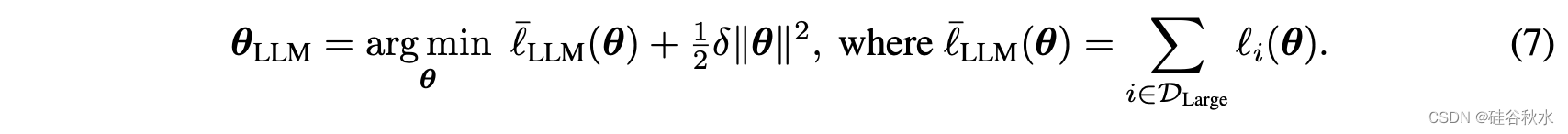
设想如下正则化器的微调：

有两个自然的问题：这样的方案试图逼近的目标模型是什么？以及TA在逼近它时犯了哪些错误？ 和以前一样，目标模型的合理选择是使用与等式（8）类似的过程进行微调而获得的，但同时在所有 Dt 上进行：

用 𝛼t 加权将目标模型与合并方案中使用的权重对齐，但这不是必需的，可以使用其他目标。 遵循与等式（6）相同的推导。 可以量化误差如下：

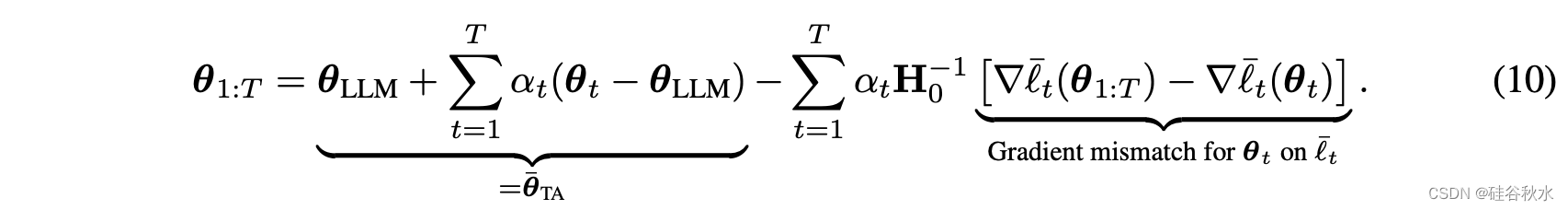
该推导可用于理解任务算术中的隐含假设。 该表达式表明，通过减少梯度失配，也许能够改进任务算术。 如下展示一种泰勒近似来减少梯度失配的简单方法，证明将 TA 与类似 Fisher 加权方案相结合是合理的。

这样有如下模型合并的策略：

其中

采用不同组合，可以说以前的方法就是公式（12）的特例，如下表所示：现有加权平均方案中的隐含假设，即AM 使用统一加权，而 TA 缺乏预处理矩阵（因为 Ht = 0）。 预计两者的梯度不匹配程度较高。 Fisher 平均方法 FA 和 FA1 都使用预处理，但忽略 θt 对 θLLM 的依赖性（因为 H0 = 0）。

梯度匹配的原理可以应用于其他合并任务和方案。 例如，当试图减少有毒语言生成时，考虑从LLMs中删除出现的任务或数据集。 对于这种情况，可以在（希望相同的）有毒数据集上微调模型，并尝试从LLMs中“减去”其贡献。采用梯度匹配，得到如下改进：

其中

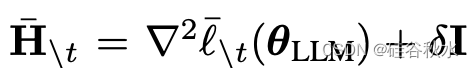
对于线性回归模型，取 𝛼t=1，则得到更新如下：

给定高斯先验和似然函数：

则有加权的后验

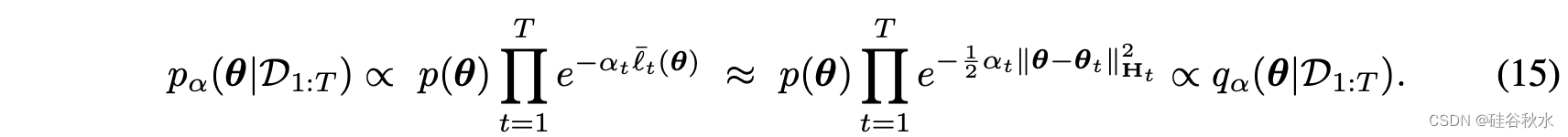
那么合并模型作为MAP（最大后验估计）如下：

这个结果将梯度失配方法与后验分布及其近似联系起来。 第一个方程将模型合并表示为在不同数据集上计算的后验 p(θ|Dt) 的合并。 使用贝叶斯方法，即使在单独的数据集上进行训练，也可以恢复精确的解决方案。 这是Bayesian committee machine (Tresp, 2000) 或贝叶斯数据融合 (Mutambara, 1998; Durrant-Whyte, 2001; Wu et al., 2022) 的一个实例，广泛用于高斯过程 (Deisenroth & Ng, 2015) ，当神经切线核（NTK）进行模型合并时，它也应该很有用（Ortiz-Jimenez，2023）。 第二个方程将现有方法与使用拉普拉斯方法获得的高斯近似连接起来。

如果梯度和Hessian如下

那么

贝叶斯连接还提供了改进模型合并并减少计算负担的直接方法。 例如，一种改进方法是采取一些优化步骤，旨在精确后验MAP 估计，然后使用当前迭代来实现等式 （10）中的泰勒近似。 随着步骤数的增加，以这种方式获得的解决方案将变得更好。 这与其他方法形成对比，例如 （Ortiz-Jimenez，2023）方法提出在线性化切线空间中进行训练，这可能并不总是收敛到正确的解决方案。 另一种改进方法是使用更好的后验近似，例如，使用变分推理（Graves，2011；Blundell，2015；Osawa，2019），这可以产生更全局近似（Opper & Archambeau， 2009）。 尽管如此，这项工作专注于改进合并，无需重新训练，并且使用计算成本低的估计，并将迭代优化作为未来的工作。

贝叶斯观点还与类似持续学习避免灾难性遗忘的努力相关（Kirkpatrick，2017），其中贝叶斯的动力证明基于 Fisher 正则化器的选择是合理的（Husza ́r，2018）。 该方法还与知识适应-先验相关（Khan & Swaroop，2021），其中通过梯度重建解决各种适应任务。 这种联系也证明了选择对角Fisher矩阵代替 Hessian 矩阵的合理性，后者本质上形成了它的广义高斯-牛顿近似（Schraudolph，2002；Pascanu & Bengio，2013；Martens，2020）。 在实验中，用对角Fisher的蒙特卡洛估计器。 这样的估计也可以在 Adam 训练期间获得（Kingma & Ba，2015），并为小批量大小提供良好的 Hessian 估计（Khan，2018）。 该估计可以是标准化的或非标准化的，也可以使用另一个 Fisher 估计。 建议根据训练数据来估计它，而不是（ Yadav 2023）提到的保留集。 （2023）。