【强化学习】CH3 动态规划

CH3 动态规划（Planning by Dynamic Programming)

3.1 简介

动态规划：将复杂问题分解成小问题进行求解。

动态：求解问题的序列；

规划：优化程序，比如策略。

常用于解决包含以下性质的问题：

• 最优子结构：子问题的解可构成总解的一部分
• 子问题有大量重复
• 马尔科夫决策过程：存在递归分解过程，值函数会反复存储与重用

在MDP问题上运用动态规划方法：

假定DP已知MDP所有环境信息：

• 预测：

​ Input:MDP$<S,A,P,R,\gamma >$和策略$\pi$

​ or MRP$<S,P^{\pi },R^{\pi },\gamma >$

​ Output:值函数$v_{\pi }$

• 控制：

  Input:MDP$<S,A,P,R,\gamma >$

  Output:值函数$v_{\pi }$和最优策略${\pi }^{\ast }$

3.2 策略评估（Policy Evaluation)

3.2.1 问题与方法

得出好策略，看看所定策略是怎么样的

问题：评估给定的策略$\pi$

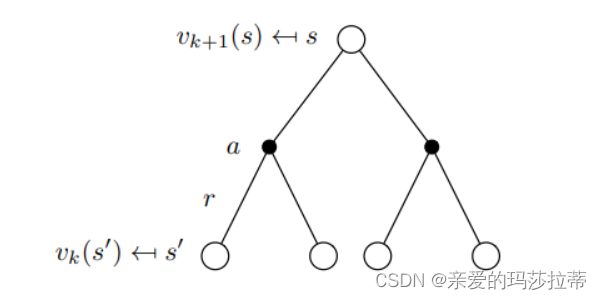
方法：贝尔曼方程的迭代使用，使用同步的方法（使用$v_k(s^{\prime })$更新$v_{k+1}(s)$）

贝尔曼方程：
$$\begin{gathered} {\mathbf{v}}^{k+1}={\mathbf{R}}^{\mathbf{\pi }}+\gamma {{\mathbf{P}}^{\mathbf{\pi }}\mathbf{v}}^k \\ {v}_{k+1}(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime })) \end{gathered}$$
下一状态值函数=当前策略的所有动作 （即时奖励+折扣因子*动作后会转移到的状态 *新状态的期望价值）

3.2.2 例题

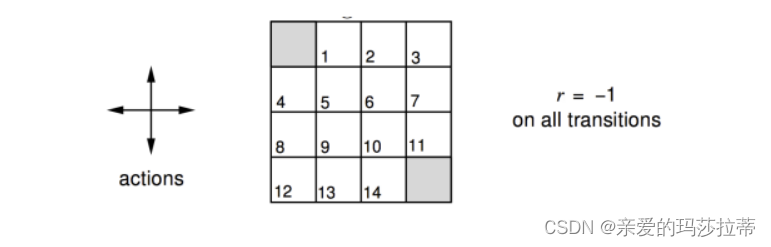
在给定四方格中，左上与右下为终止状态，个体以1/4的概率向上下左右移动，越过边框则反弹，所有状态的及时奖励均为-1，折扣因子为1，求取各步骤k的值函数

求解：

**无贪婪处理：**无论经过多少步，用户的策略都是以1/4的概率向上下左右。

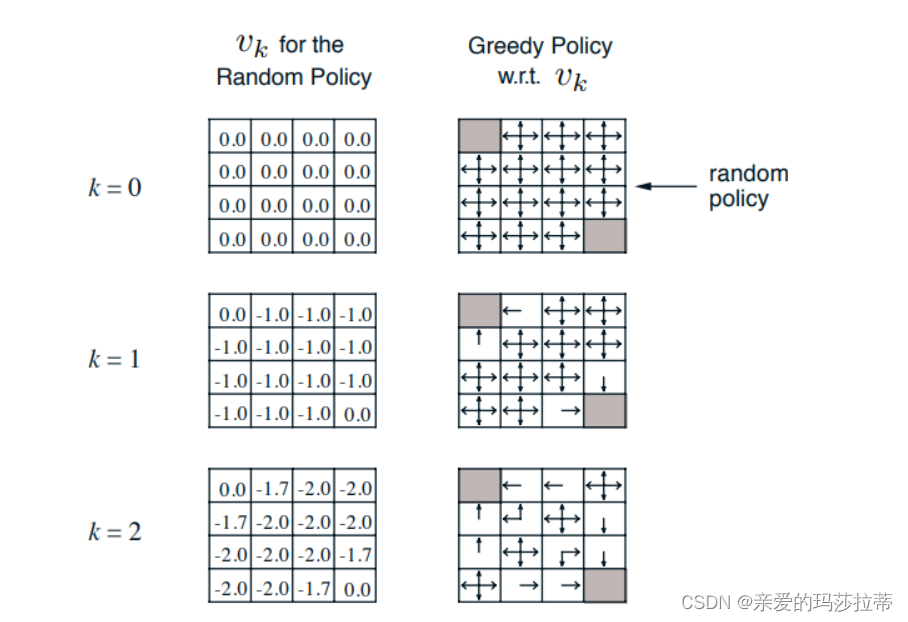
计算 从k=1到k=2的(1,2) 位置的值函数：
$$\begin{gathered} v_{k+1}(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime })) \\ =上（回到原地）+下（到（2,2））+左（终止）+右（到（1,3）） \\ =1/4\ast (-1+1\ast (1\ast (-1.0)))+1/4\ast (-1+1\ast (1\ast (-1.0)))+1/4\ast (-1+1\ast (1\ast (0)))+1/4\ast (-1+1\ast (1\ast (-1.0))) \\ =-1.75 \end{gathered}$$
注：这里经过一个动作到达的状态的固定的，如个体向上会以概率1回到原地。

这里没有贪婪处理，无论经过多少步，用户的策略都是以1/4的概率向上下左右。

最终仅评价每个位置的值函数。

3.3 策略迭代（Policy Iteration)

3.3.1 贪婪处理

在得到值函数的过程中，一步步优化策略

${\pi }^{\prime }=greedy(v_{\pi })$ 贪心地选择最优策略，加快收敛速率

计算**从k=1到k=2的(1,2)**位置的值函数：

经过k=0->k=1的贪心策略优化后，（1,2）位置的策略为向左
$$\begin{gathered} v_{k+1}(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime })) \\ =左（终止） \\ =1\ast (-1+1\ast (1\ast (0))) \\ =-1 \end{gathered}$$

此操作满足压缩映像原理，最终值函数均会收敛到最优${\pi }^{\ast }$

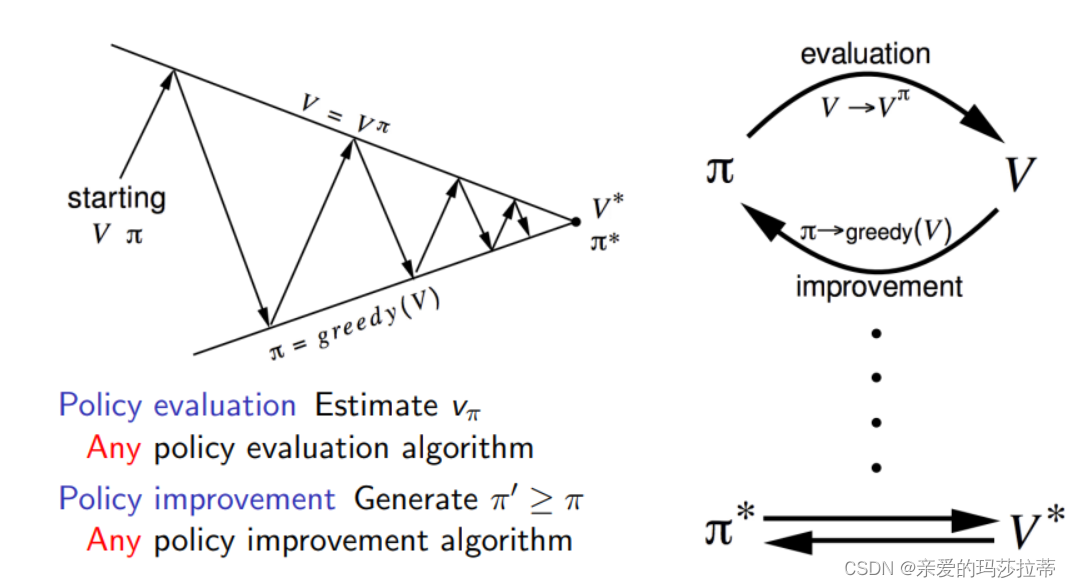
证明：

每一步都是最优策略，最后一定也是最优策略。

注：

• 策略评估不一定要收敛完成

• 早停机制：固定迭代次数或者值函数差小于收敛阈值即结束

• 策略迭代等价于值迭代

3.4 值迭代（Value Iteration)

优化策略可分为两部分：优化的动作和下一状态

最优化理论：

一个策略$\pi (a|s)$自状态s到达最优值函数$v_{\pi }(s)=v_{\ast }(s)$,当且仅当

• 从s可到达任何状态s’
• $\pi$已经是从s’出发的最优策略了$v_{\pi }(s’)=v_{\ast }(s^{\prime })$

3.4.1 问题与方法

问题：寻找策略$\pi$

方法：贝尔曼方程的迭代使用，使用同步的方法（使用$v_k(s^{\prime })$更新$v_{k+1}(s)$）

​ 没有显性的策略；中间值函数可能不与任何策略对应

贝尔曼方程：
$$\begin{gathered} {\mathbf{v}}^{k+1}=ma{x}_{a\in A}({\mathbf{R}}^{\mathbf{\pi }}+\gamma {{\mathbf{P}}^{\mathbf{\pi }}\mathbf{v}}^k) \\ {v}_{k+1}(s)=ma{x}_{a\in A}(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime })) \end{gathered}$$
下一状态值函数=当前策略的拥有最大值函数的动作 （即时奖励+折扣因子*动作后会转移到的状态 *新状态的期望价值）

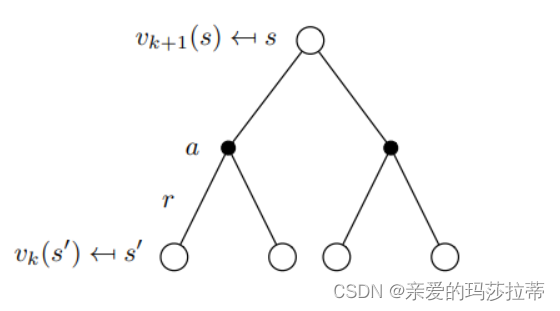
3.4.2 值迭代例题

完全不考虑策略，直接以最优的v(s)更新，试探各个方向，贪心选择值函数最大的方向
$$v_{\ast }(s)<-ma{x}_{a\in A}{R}_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime })$$

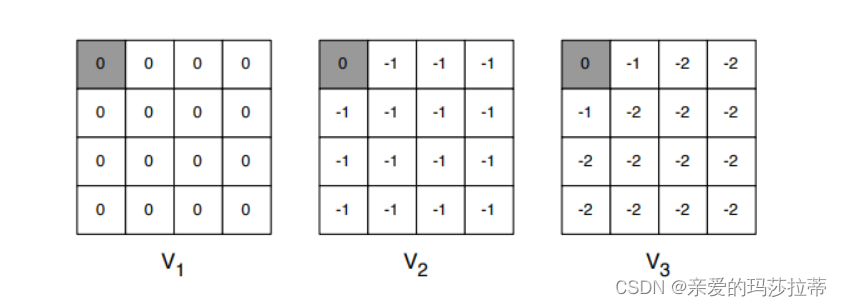
计算**从k=2到k=3的（1,2）**位置的值函数：
$$\begin{gathered} v_{\ast }(s)<-ma{x}_{a\in A}{R}_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime }) \\ {v}_{\ast }(s)<-max((-1+1\ast (1\ast (-1.0))),(-1+1\ast (1\ast (-1.0))),(-1+1\ast (1\ast (0))),(-1+1\ast (1\ast (-1.0)))) \\ {v}_{\ast }(s)<-(-1) \end{gathered}$$

3.5 对比分析

	策略评估	策略迭代	值迭代
应用于	评估已知的策略（预测）	选择最优的策略（控制)	选择最优的策略(控制)
方法	贝尔曼方程的迭代使用，使用同步的方法（使用$v_k(s^{\prime })$更新$v_{k+1}(s)$）	在得到值函数的过程中，贪心地选择最优策略，加快收敛速率	完全不考虑策略，直接以最优的v(s)更新，试探各个方向，贪心选择值函数最大的方向
公式	$v_{k+1}(s)={\sum }_{a\in A}\pi (a|s)(R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime }))$	$v_{k+1}(s)={\sum }_{a\in A}\pi (a|s)(R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime }))$	$v_{k+1}(s)=ma{x}_{a\in A}(R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_k(s^{\prime }))$
特点	全过程策略保持不变，不停计算值函数	计算值函数与策略优化选择交替进行	无策略，直接选择动作的最优值函数复杂度
复杂度	$O(m{n}^2)$ m:动作数 n:状态数	同左	$O(m{n}^2)$ m:动作数 n:状态数

3.6 异步DP

所有状态可并行更新，值函数表中新旧交替且并存