二阶滤波器（开荒篇）

 引言：为什么需要使用二阶滤波器呢？因为在一阶滤波器中超过截止频率的部分衰减幅度比较小，在有些情况并满足不了我们的需求。一阶滤波器的增益通常是每过10倍频为-20dB，而二阶滤波器可以达到-40dB。在相同信号的情况下，相比一阶，二阶可以把该信号的增益降到更低。

简单有源二阶

首先我们来看一阶滤波器的仿真图

    根据幅频特性曲线来看，该低通滤波器的截止频率在1.6khz左右，运放在此刻做的是电压跟随器的作用，没有放大倍数的作用。

（截止频率计算公式：1/2ΠRC 不懂的可以去这里看，这里有详细的说明）滤波器初步入门（非常全面）-CSDN博客

我们来看看二阶滤波器的设计仿真结果

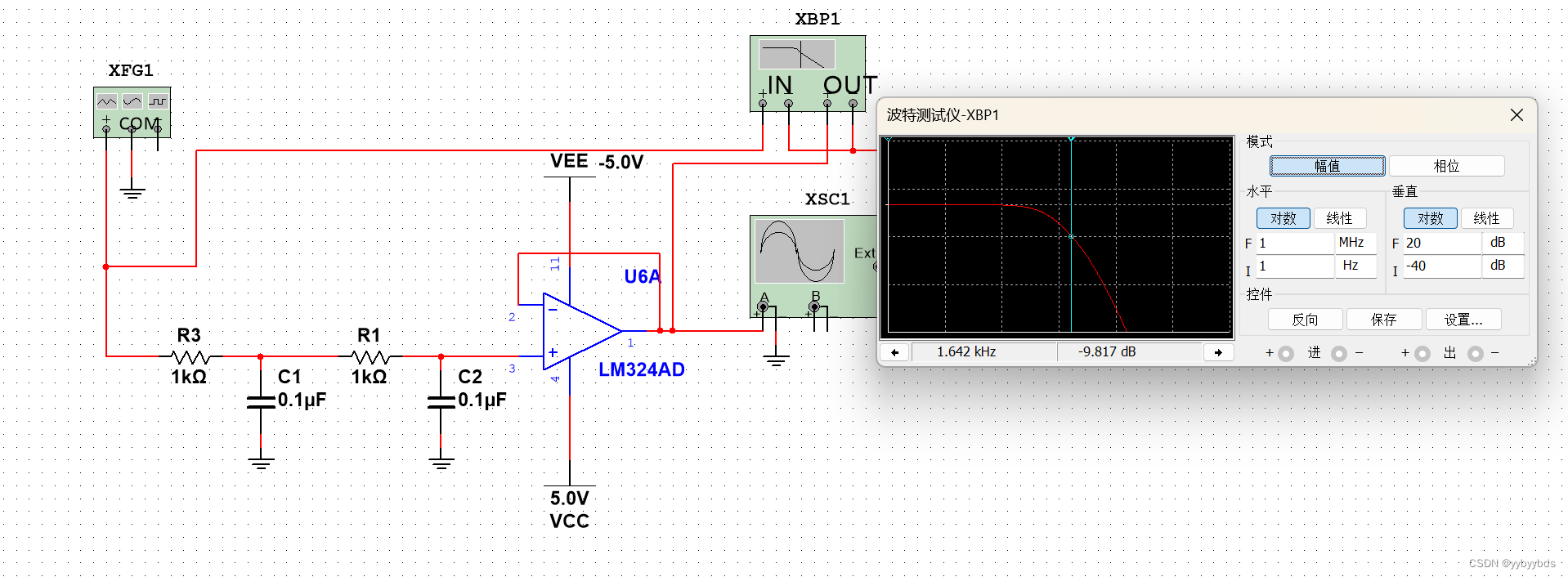
可以看到过渡带的曲线明显比一阶滤波器的更加陡了，也就是衰减的幅度更大了，但是出现了一个新的问题，就是原来的截止频率的衰减也会更多，从-3dB增大到-9dB了，此刻的截止频率就从原来的1.6khz到500多hz了。（如下图）

根据推算得出以下结果

这个简单二阶滤波器的截止频率会变成原来一阶滤波器的0.37倍。

为了截止频率不要衰减的那么快，尽量保持在原先的截止频率，于是新加了一个正反馈，对这个电路进行一个改进。

压控电压源二阶LPF

该电路的优点是可以把想要输出的频率进行指定额外的放大输出，而且可以不影响其他频率的增益

如下图（低通）

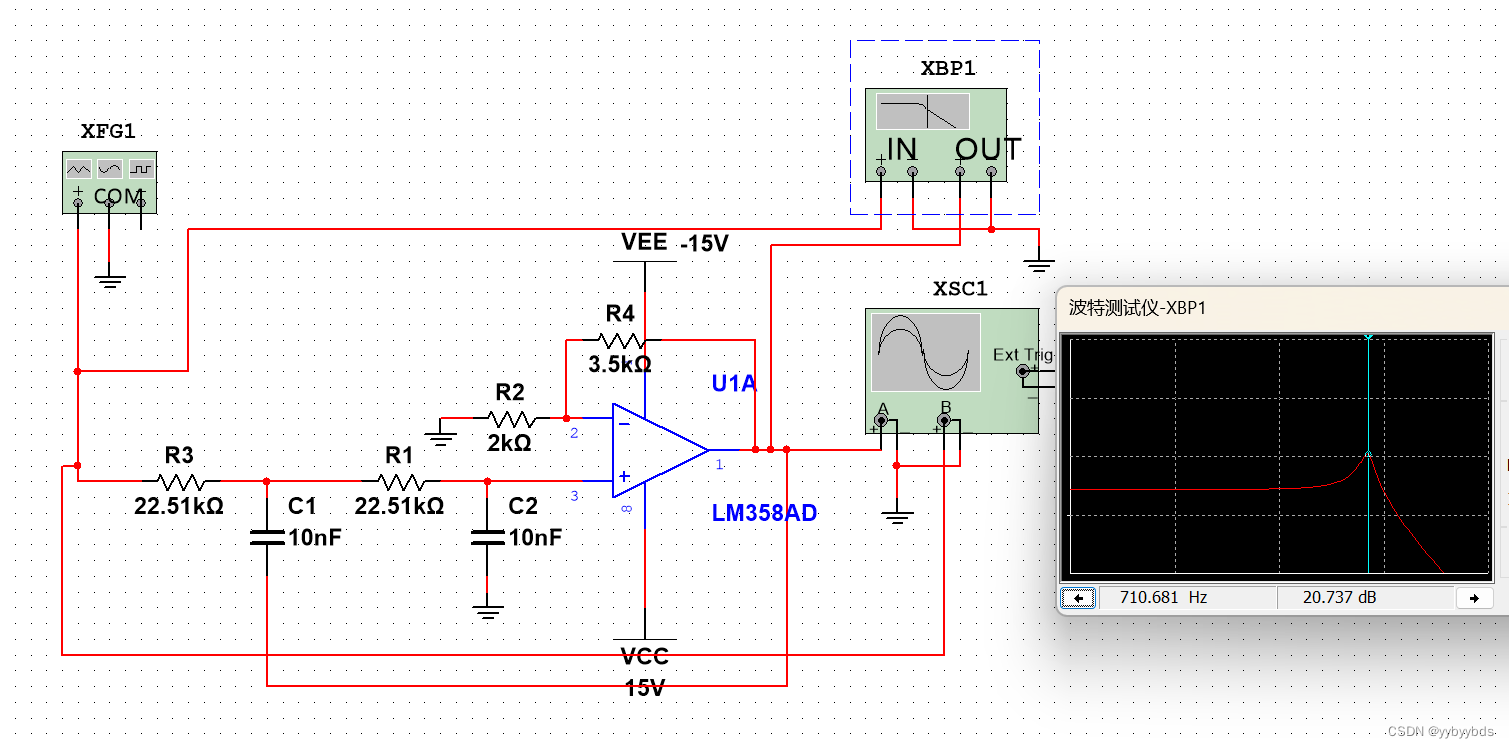
当f在指定频率时放大增益为20dB，而通带和过渡带的频率因为运放的影响增益为（1+R4/R2），两者互不影响。（这里的f是1/2ΠRC）

过渡带会受到这个放大倍数影响

品质因素决定了这个指定频率的放大倍数，但品质因素和放大倍数不是直接关系

品质因素

右上角为品质因素公式，Aup是通带放大倍数，当2<Aup<3时（1<Rf/R1<2），Q>1，此时当Aup越接近于3时，品质因素越大放大倍数越大，当Au=2时，Q=1，放大倍数为通带的放大倍数。当1<Au<2时，Q<1,此时增益为负，Q越小越明显。（需要注意的是Aup不能大于3，否则会引起自激振荡）

当2<Aup<3时（该电路的f=700hz）

当Au=2时

当1<Au<2时

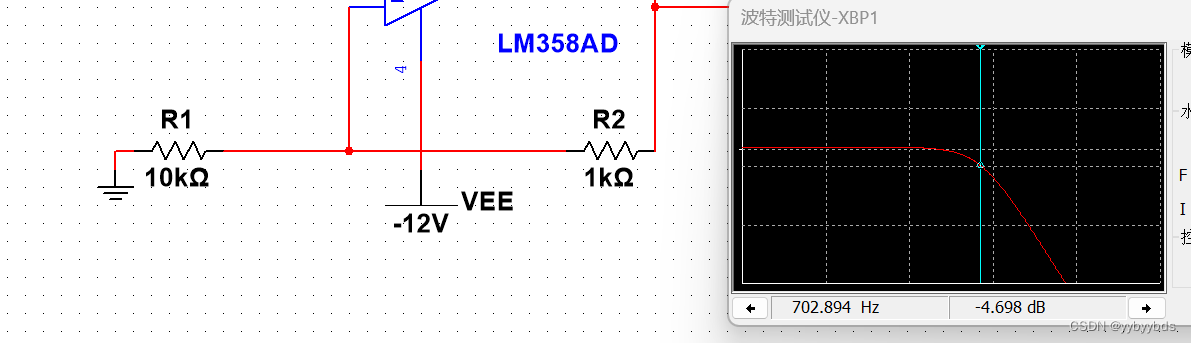
R1R2阻值要调高点，因为现实中电阻有误差，电阻太小一点误差就会导致增益出现很大的变化

如果不用放大信号的话，该电路的放大信号会增加一些不稳定因素。可以降上面电路改进一下，将Q设成1，也就是变成电压跟随器，并改一下其中一个电容的大小。

简化的二阶低通滤波

该电路的截止频率如图

仿真图，上面是改进后的电路，下面是最简单的二阶滤波器

他们两个的差别在于用同样的元器件，加了正反馈的电路可以获得更大的带宽。

二阶高通滤波电路

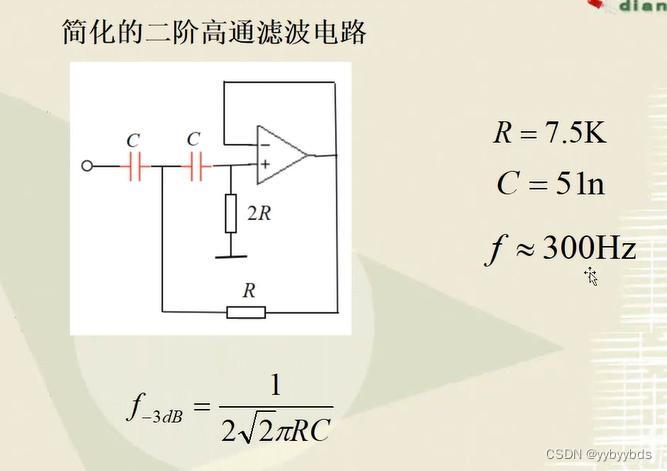
相比低通就是R3去接在运放的输出端

带通滤波器

如果要设置一个带通滤波器（300hz~3k），那么就可以用低通和高通组成，低通的截止频率要在3k，高通的截止频率为300hz。

这是一个放大倍数为1的带通滤波器。

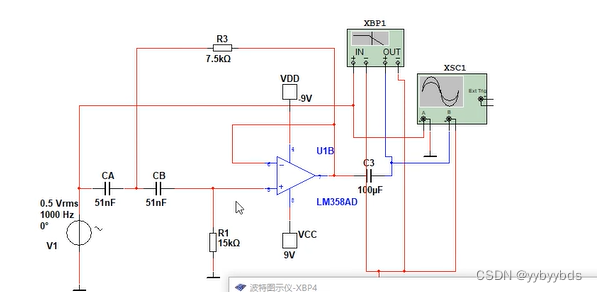
单电源运放（以上面的带通滤波器为示例）

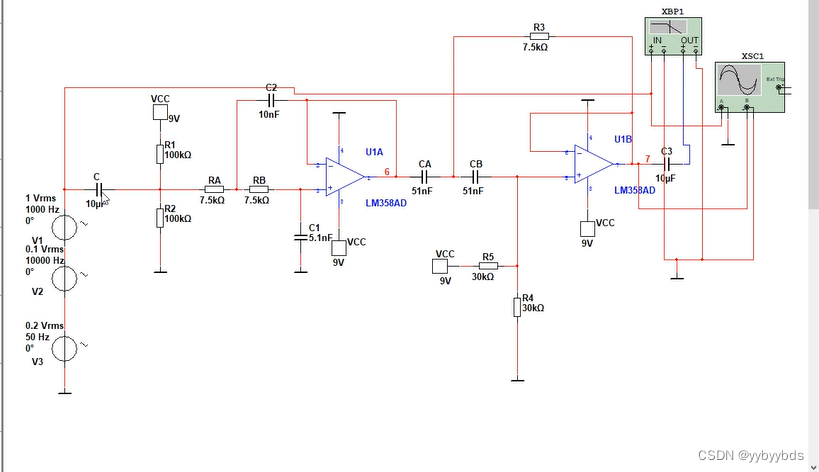
此电路需要在输入加入一个偏置电压，注意加偏置电压时候要与输入信号之间加一个电容（10uf）

偏置电压也可以这样加，本来电阻为15k，但将两电阻并联后也等于15k使用可以等效替换，如何再加入电压中间就会有4.5V的分压，由于前面本身就有电容所以不用额外在加一个。

总结：相对一阶电路来说，二阶的过渡带更为陡峭，能满足一些需求，二阶分简单和压控电压源二阶（有放大和无放大），他们的区别是简答的截止频率会比一阶的低很多，在元器件选型时可能更加麻烦，所以通常使用压控电压源二阶。

补充：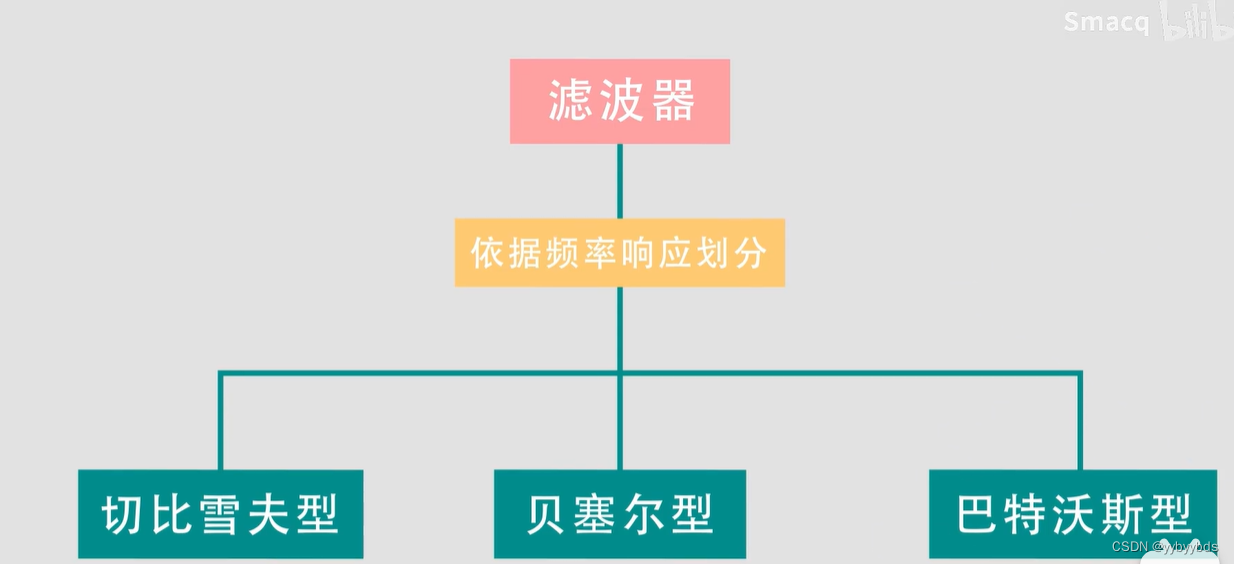

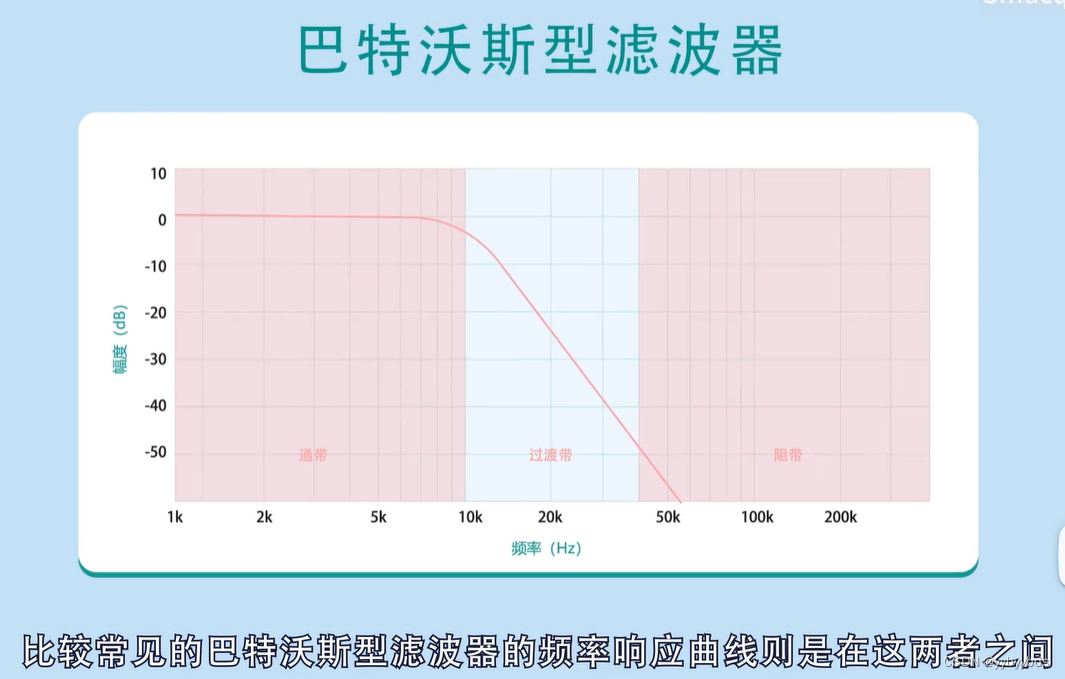
下面以低通滤波器来说明他们是如何划分的：

过渡带的频率曲线比较陡峭，通频带的曲线有明显变化

当频率响应曲线在过渡带比较缓和，且通频带没有明显波动时