SVM-7-SMO（序列最小优化算法）

参考http://www.cnblogs.com/jerrylead

坐标上升法

首先介绍坐标上升法（Coordinate ascent）：
假设要解决下面的没有约束的最优化问题：

$$\max_\alpha \ W(\alpha_1,\alpha_2,...,\alpha_m)$$ .
对于这类最优化问题，我们可以使用地图下降法或者牛顿迭代法，这里我们使考虑使用坐标上升法：

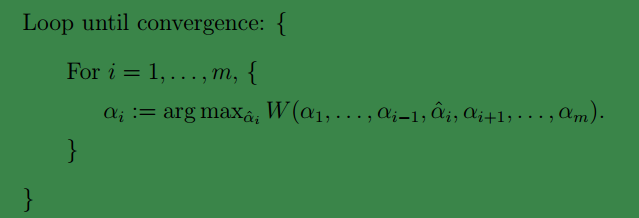
也就是说，每次循环我们我们固定除当前 $\alpha_i$之外的所有 $\alpha_j(j \not =i)$。每次循环，W只看作是关于当前 $\alpha_i$的函数，此时只需直接对 $\alpha_i$求导优化即可。然后依次进行m循环。
在优化是，我们可以通过调整优化的 $\alpha$的顺序提高算法的性能。

下图展示了坐标上升法：

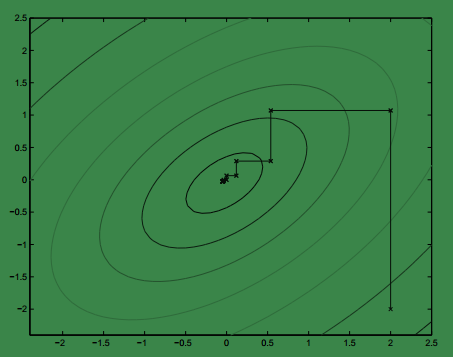
上图中中的椭圆代表我们要优化的二次方程的轮廓，最优值就是中心的黑点，我们的初始值在右下角（2，-2），从图中可以看出，每次都平行于某个坐标轴，因为每次我们只优化一个变量。

SMO

现在重新新回到我们要优化的问题（原问题的对偶问题）：

$$\max_\alpha\ W(\alpha)= \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}y^iy^j\alpha_i\alpha_j<x^i,x^j>\\ \qquad s.t.\ 0\leq\alpha_i\leq C,\ i=1,...,m\\ \sum^m_{i=1}\alpha_iy^i=0$$
假如我们有满足上述约束的 $\alpha$的集合，那么我们能直接使用上面的坐标上升算法吗？
假设我们保持 $\alpha2,...\alpha_m$固定不变，利用坐标上升通过改变 $\alpha_1$的值来优化问题，这样可行吗？答案是不行！

因为根据上面的等式约束条件我们可以得到：

$$\alpha_1y^1=-\sum^m_{i=2}\alpha_iy^i$$
由于 $y\in\{-1,1\}$，因此上式可以改写成：
$$\alpha_1=-y^1\sum^m_{i=2}\alpha_iy^i$$
可以看出， $\alpha_1$的值是和 $\alpha2,...\alpha_m$相关联的。

因此我们一次最少选取两个变量才能满足约束。然后SMO算法就诞生啦：

可以看到每次选取$\alpha_i,\alpha_j$时都根据经验选取最好的一对组合。
然后固定除$\alpha_i,\alpha_j$之外的参数，进行优化。
SMO 之所以高效就是因为在固定其他参数后，仅对两个参数$\alpha_i,\alpha_j$优化的过程很高效。

现在假设我们有满足约束条件的参数集合$\{\alpha_1,...\alpha_m\}$，假设固定$\{\alpha_3,...\alpha_m\}$，这样W就是$\alpha_1和\alpha_2$的函数，且根据等式约束$\alpha_1和\alpha_2$满足下式：

$$\alpha_1y^1+\alpha_2y^2=-\sum^m_{i=3}\alpha_iy^i$$
因为 $\{\alpha_3,...\alpha_m\}$以固定，为了方便，我们用 $\zeta$代替等式右面：
$$\alpha_1y^1+\alpha_2y^2=\zeta$$
显然我们可以改写成： $\alpha_1=(\zeta-\alpha_2y^2)y^1$

我们可以用下面的图说明$\alpha_1,\alpha_2$取值情况，以及它们的关系:

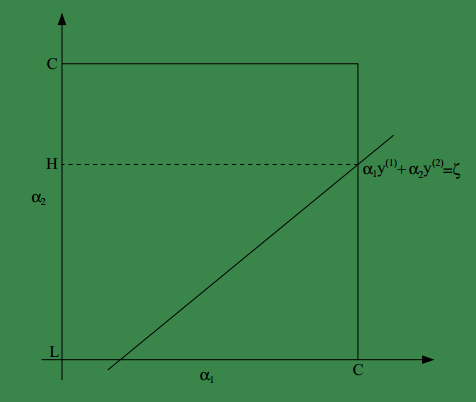
横轴是$\alpha_1$纵轴是$\alpha_2$，从之前的KKT约束条件我们已经知道$\alpha$的取值范围是[0，C]，因此$\alpha_1,\alpha_2$的值必然在[0,C]X[0,C]的矩形框内。并且在上图中$\alpha_1,\alpha_2$必然在直线$\alpha_1y^1+\alpha_2y^2=\zeta$上，因此必然存在$0\leq L \leq H \leq C$使得，$L \leq \alpha_2 \leq H$。

现在我们可得：

$$W(\alpha_1，\alpha_2,...\alpha_m)=W((\zeta -\alpha_2y^2)y^1,\alpha_2,...,\alpha_m)$$
同样的对于 $\{\alpha_1,...\alpha_m\}$我们也可以用 $\alpha_2$来表示。
因为我们的优化问题是一个2次方程（ $就那\max \frac{1}{2}||w||^2什么的$），因此现在我们可以将它表示成一个关于 $\alpha_2$的2次方程,例如： $a\alpha_2^2+b\alpha_2+c$。
这样我们就可以通过求导直接计算出函数的最优值。当然我们同时也要保证 $\alpha_2$满足约束。
将在不考虑约束的情况下求得的 $\alpha_2$的值表示成 $\alpha_2^{withoutconstraints}$，由于 $\alpha_2$的取值范围是[L,H]
可通过如下方式确定 $\alpha_2$的值:
$$\begin{eqnarray} \alpha_2= \left \{ \begin{array}{lll} H & \textrm{if$\ \alpha^{withoutconstraints}_2>H$}\\ \alpha_2^{withoutconstraints} & \textrm {$if\ L\leq \alpha_2^{withoutconstraints} \leq H$}\\ L & \textrm{$if \ \alpha_2^{withoutconstraints} < L$} \end{array} \right. \end{eqnarray}$$
然后我们就可以通过 $\alpha_2$得到其他的 $\alpha$的值了。