抽点时间读经典AI论文之Learning representations by back-propagating errors

这篇论文讲述的是世界上第一篇反向传播算法,标题的意思是通过反向传播错误来学习表征

在读这篇论文时,我是带着这三个问题去读的:

1. 作者试图解决什么问题?
2. 这篇论文的关键元素是什么?
3. 论文中有什么内容可以"为你所用"?

于此同时,在讲解这篇论文时,我不会把论文全篇翻译出来,毕竟这样做毫无意义,我会把我个人觉得比较重要的部分摘出来,再结合我自己的认识,与大家分享

文章的一开头就给出了反向传播算法的原理:

The procedure repeatedly adjusts the weights of the connections in the network so as to minimize a measure of the dilference between the actual output vector of the net and the desired output vector.

该程序反复调整网络中连接的权重，以使网络的实际输出向量与期望输出向量之间的偏差最小化。

其实这个过程就是学习的过程,学习率就是用来调整权重的超参数,举个最简单的例子,输入一个数,如何让机器输出相反数呢?

不难知道,让这个数乘上-1即可,这个-1其实就是网络的权重,如果用数学表达,可以列出如下式子:

Y = A * X

• Y表示网络的输出,即相反数
• A表示权重,就是网络要学习的参数
• X表示输入网络的值,理论上可以是任意一个数

权重A在开始时可以随机设定一个数,比如1;如果学习率是0.1,那么需要至少20轮训练,才能让权重A从1变成-1

如果你看懂了这个过程,那么你可以看看我的这篇文章:

如何用Python教机器学会牛顿第二定律?

接着,论文提到了隐藏层,并描述了什么是隐藏层:

In perceptrons,there. are ‘feature analysers’ between the input and output that are not true hidden units because their input connections are fxed by hand, so their states are completely determined by the input vector: they do not learn representations.

简单来说,隐藏层是用来提取特征的。比如我输入了10个特征,隐藏层只定义5个特征,那么这就相当于把这10个小特征合并成了5个大特征,当然,你也可以根据需要,再把这5个特征合并

需要注意的是,这些特征都是人为定义好的,举个具体点的例子,在做人脸分析时输入图片的特征有肤色、发型、是单眼皮还是双眼皮、鼻子的大小等,然后将这些特征输入到人为定义好的隐藏层中,假如隐藏层定义的特征是好看、一般和不好看,那么输出的特征就会更抽象

也就是说,隐藏层的作用就是把具体的特征变得抽象

读到这里,不知道你有没有疑惑,隐藏层到底是怎么样把具体的特征变得抽象的?作者给出了两个公式:

• $x_j$ = ${\sum }_i{y}_i{w}_{ji}$     (1)

• $y_j$ = $\frac{1}{1+e^{-x_j}}$        (2)

具体怎么用呢?这里举个例子:

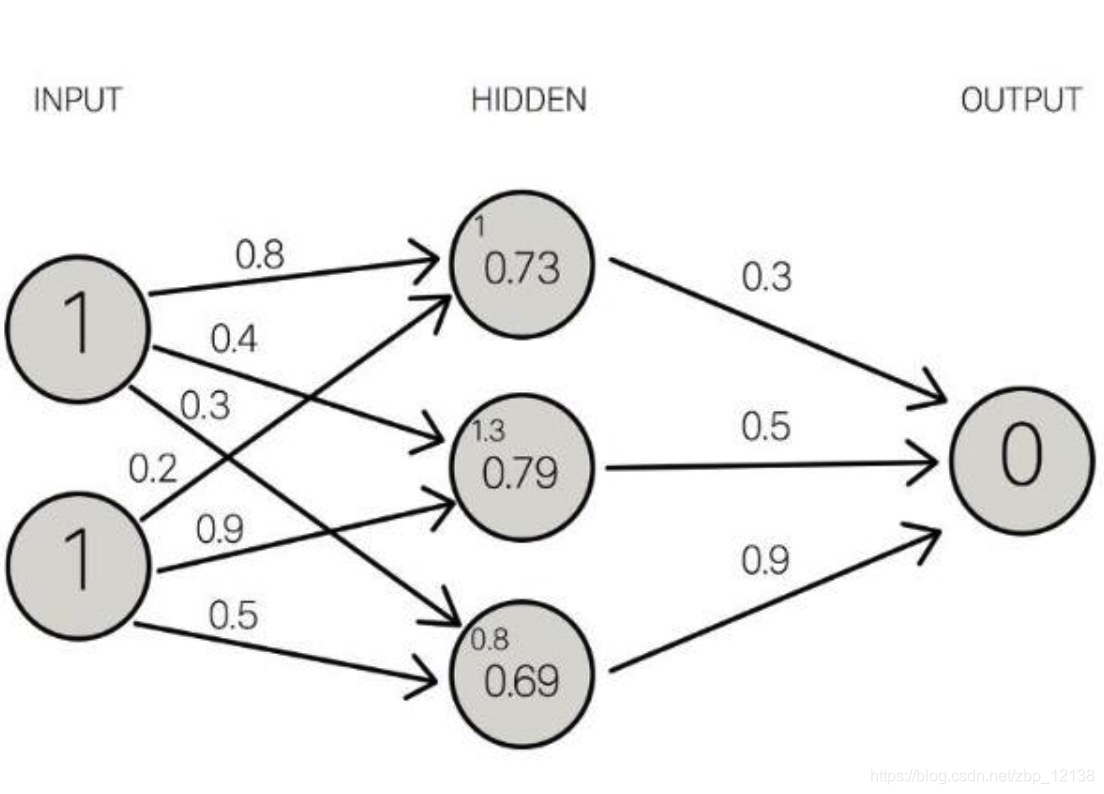
假设有两个输入,分别是1,箭头上的数字代表权重,箭头的指向表示输出,下面我们来算一下第一个隐藏层的输入值$x_1$ = 1 * 0.8 + 1 * 0.2 = 1

第二个隐藏层的输入也不难得到:
$x_2$ = 1 * 0.4 + 1 * 0.9 = 1.3

同理,$x_3$ = 1 * 0.3 + 1 * 0.5 = 0.8

上面用的就是公式(1),而公式(2)其实就是Sigmoid函数,我们把三个输入值带进Sigmoid函数算一下:

四舍五入后就得到了输入层的输出,输入层的输出就是隐藏层的输入。推广一下,其实就是上一层的输出是下一层的输入。

这句话也对应着论文里的描述:

The simplest form of the learning procedure is for layered networks which have a layer of input units at the bottom; any number of intermediate layers; and a layer of output units at the top. Connections within a layer or from higher to lower layers are forbidden, but connections can skip intermediate layers. An input vector is presented to the network by setting the states of the input units. Then the states of the unils in each layer are determined by applying equations (1) and (2) to the connections coming from lower layers. All units within a layer have their states set in parallel, but diferent layers have their states set sequentially, starting at the bottom and working upwards until the states of the output units are determined.

作者随后又说,其实没必要完全使用前面的公式(1)和公式(2):

It is not necessary to use exactly the functions given in equations (1) and (2). Any input-output function which has a bounded derivative will do. However, the use of a linear function for combining the inputs to a unit before applying the nonlinearity greatly simplifes the learning procedure.

并解释了这样做的目的