梯度下降和反向传播：能改(升级截距)

背景

了解 现代神经网络算法的精髓(梯度下降算法)后，如果仔细观察 我们设计的预测函数，会发现 这是一个非常危险和不完善的模型。

问题

比如，在另外一片海域里，豆豆的大小和毒性的关系是这样的。

有些太小的豆豆是不存在的

我们发现不论怎么调整w,都无法得到理想的预测函数

更加糟糕的情况是，豆豆越大，毒性越低，这样我们设计的预测函数就完全不对了。

原因

我们的预测函数y=wx 很明显，是一个必须经过原点 的直线，换句话说，这个预测函数的自由度被限制了。只能旋转，而不能移动。

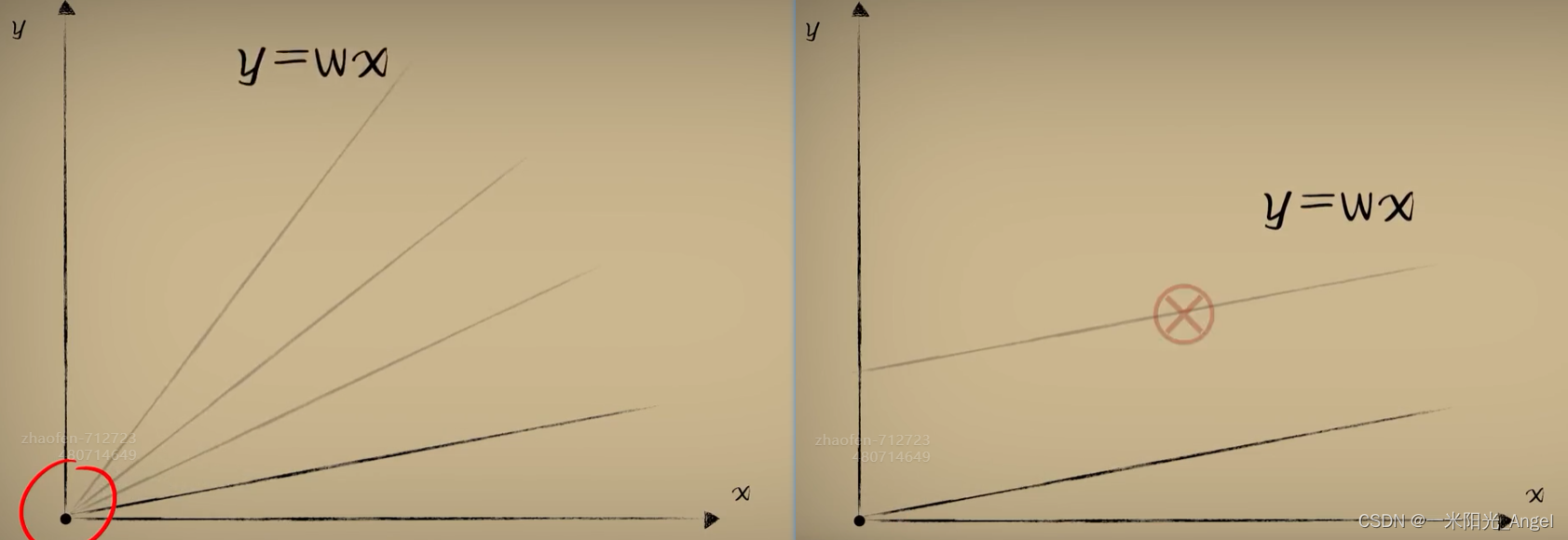
其实，一个直线完整的函数应该是：y=wx+b
之前，我们为了遵循“如无必要，勿增新知”的理念，一直在刻意避免这个截距参数b
直到现在，我们终于避无可避，是时候增加“新知”了
截距b作用 可以让直线在平面内自由的平移
斜率w作用 可以让直线在平面内自由的旋转
这两者结合，让直线在整个平面真正的自由。

当带入b后，重新推演一次预测和梯度下降过程。
为了简单起见，我们先采用单个样本，代价方差函数的结果是这样的：

当没有b 或者 b=0 的时候，方差代价与之前一样
所以说，之前的情况是b=0的特殊情况

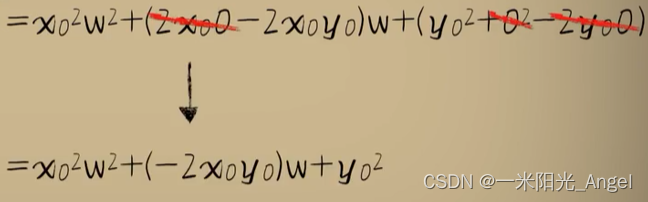
现在既然有了 b ,接下来，我们要看 b 取不同值的时候，对方差代价函数的影响。
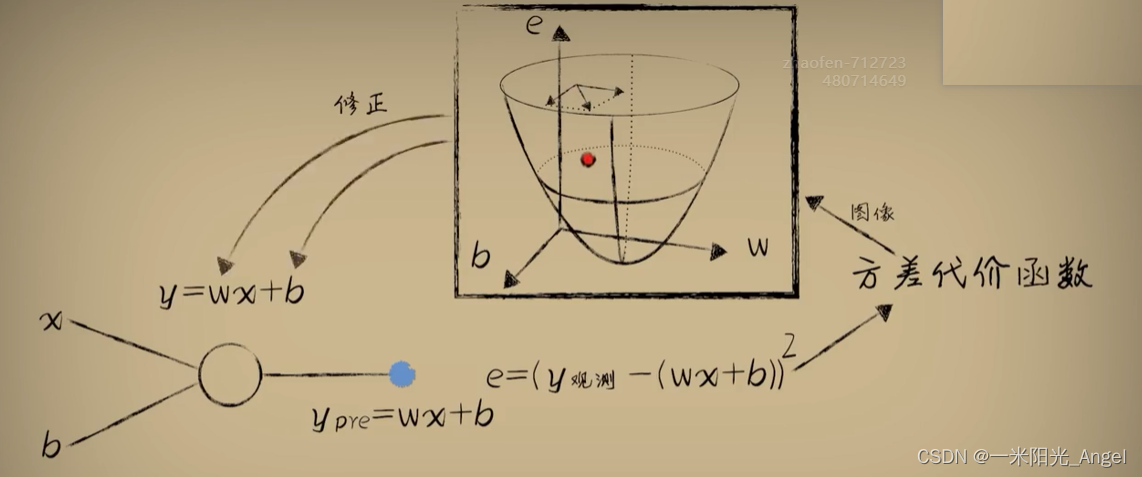
这里，我们需要把代价函数的图像由二维变成三维，给b留出一个维度

根据方差代价函数可以看出，b改变的只是抛物线的具体样子，而不是使它变成其他形状

我们通过 b 的不同取值，在三维图像上画线，可以看出一些眉目
图像是一个三维空间的曲面

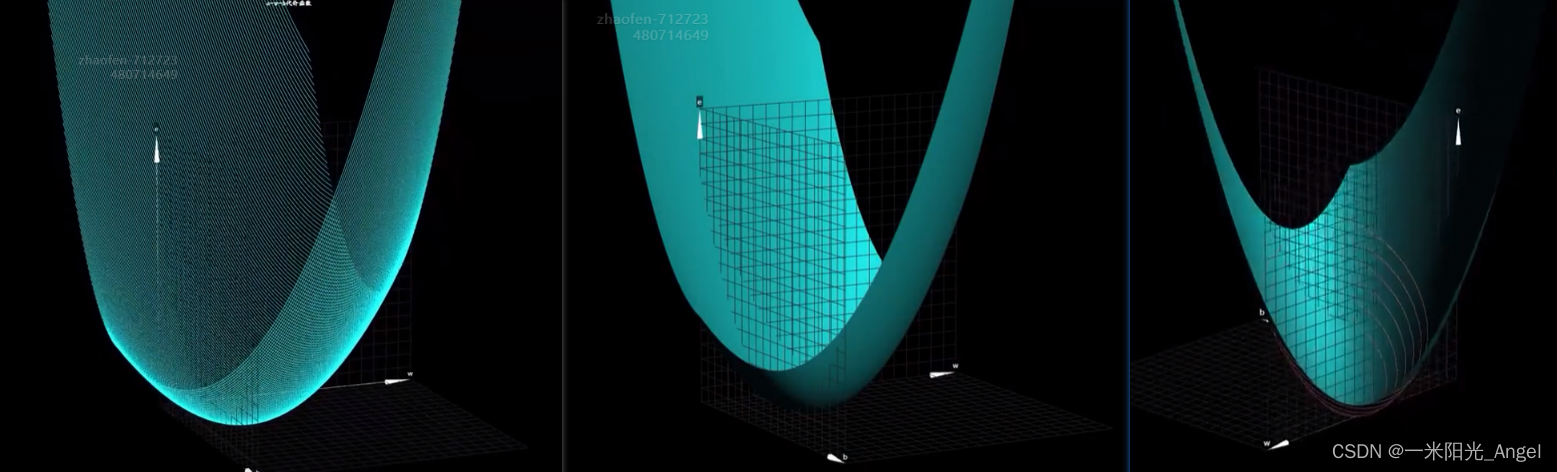
我们该如何看待这个曲面？
很多教程和书籍中，为了看着明显，很多时候，将它画成一个鼓鼓的碗状

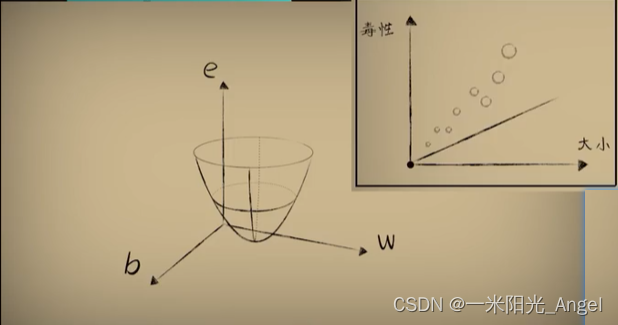
其实，对于线性回归问题中，这种豆豆数据形成的代价函数，实际上并没有那么鼓，而是一个扁扁的碗，扁的几乎看不出来是个碗，但当我们把这个曲面的等高线画出来时，就可以看出来，这确实是一个碗。

关键

很明显，这个碗状曲面的最低点，肯定是问题的关键

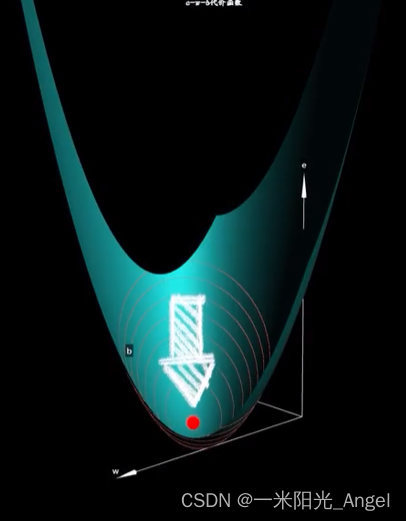
在没有b出现时，曲线最低点代表w的取值造成的预测误差最小

首先，曲面最低点的形成，每次取不同的w和b,都会导致误差e不相同

这个曲面就是带入b后得到的代价函数的图像，这里的w和b的取值会让预测的误差（代价）最小

如果能找到最地点 w 和 b 的值，放回到预测函数中，此时此刻，恰如彼时彼刻，预测也就是最好的

解决

如何取得这个曲面上最低点处的w 和 b 的值？
首先，在b=0 处，沿着w的方向切一刀，这将形成一个关于 e 和 w 的开口向上的抛物线
根据前面的内容可知，不断通过梯度下降算法，调整w，最后到达最低点

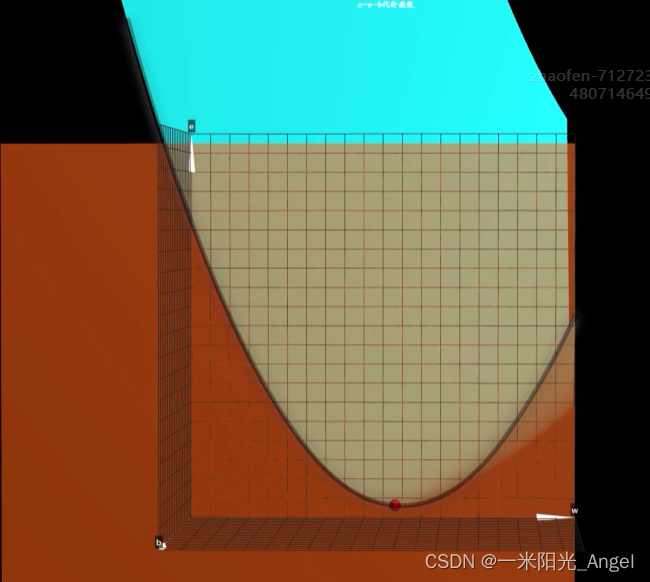
我们会发现，曲线的最地点，并不是这个曲面的最低点

这个时候，如果我们沿着 b=0 的方向给曲面来一刀，我们会发现，切面也是一个开口向上的抛物线

e 和 b 的关系，通过整理可得，当w固定时，也是一个标准的，开口向上的，一元二次抛物线

换个角度，去理解曲面的形成方式：除了一开始那样，认为是e关于w的一元二次函数曲线在b取不同的值的时候形成的以外；也可以认为是e关于b的一元二次函数曲线在每次w取不同的值的时候形成的。现在我们在b上要做的事情和在w上一毛一样，不断的调整b,让它向这个曲线的最低点挪动，而具体的方法也是一样的，根据斜率进行下降。

我们完整来看一下这个过程：
假如一开始 w=0.1 b=0.1 ,对应的e在曲面的这个位置

正所谓 横看成岭侧成峰。
我们横看此处，看见的是在b确定的时候e和w形成的一个曲线，根据此处的斜率（导数）调整w。我们侧看此处，看见的是在w确定的时候e 和 b 形成的一个曲线，根据此处的斜率（导数）调整w。

把这两个方向上的调整运动合成一个合成调整运动，这样完成一次调整，到达下一个点后我们继续横看调整w，侧看调整b，当我们反复的进行这个过程的时候，也就逐渐向曲面最低点挪动。

所以说 这里同时有w 和 b 的代价函数曲面 和只有w 的代价函数曲线相比，这个下降的过程的本质是一样的，换汤不换药罢了；或者说只是从w一味药换成了w 和 b 两味药。
但有一点，我们的代价函数已经是一个曲面了，这个下降的过程 如果再称之为 “斜率下降”就不太合适了。
毕竟一个曲面上某点的“斜率”是什么东西呢，是关于w 的呢，还是 关于 b 的呢？

要回答这个问题，需要发散一下思维，换一个角度来看这个下降的过程：
我们在代价函数的w和b两个方向上分别求得斜率
对于有两个自变量的代价函数，我们先偏向w求导数，在偏向b求导数

为了区分只有一个自变量的情况，我们把在某个变量上的导数也称为“偏导数”
如果我们把对w和对b的偏导数看作向量，把着两个向量合在一起，会形成新的和向量，沿着这个合向量进行下降，是这个曲面在该点下降最快的方式，这个合向量在数学里称之为“梯度”

梯度是一个比向量更为“广泛"的一个概念，她是把各个方向上的偏导数（斜率），当作向量合起来形成一个总向量，代表着这个点下降最快的方向

在二维曲线中，因为没有别的其他方向，梯度和斜率可以认为是一会儿事，而为了让这个下降算法的名字更具有广泛性，所以，我们一般称之为“梯度下降”

总结

我们从环境中观察到了一个问题：

豆豆的毒性和它的大小有关系
现在想要准确的去预测这个关系到底是什么
按照McCulloch-Pitts神经元模型，我们使用一个一元一次线性函数，去模拟神经元的树突和轴突的行为，这就是预测函数模型。

把我们统计观察而来的数据送入预测函数得到进行预测的过程，称之为前向传播，因为计算从前往后。

数据通过预测函数完成一次前向传播就会得到一个预测值
预测值和统计观测而来的真实值之间存在误差
我们选择平方/均方误差作为误差的评估手段
会发现这个误差和预测函数中的参数又会形成一种函数关系
我们把这个函数称之为代价函数
因为采用方差（平方误差的简写）去评估预测误差
所以，也称之为 方差代价函数
描述了预测函数的参数取不同值时的时候，预测的不同的误差代价
而用这个代价函数去修正预测函数参数的过程，也称之为 反向传播
因为计算过程，从后往前。
而这个反向传播的参数修正的方法，我们使用梯度下降算法

在没有截距b的二维代价函数中，叫“斜率下降”也未尝不可
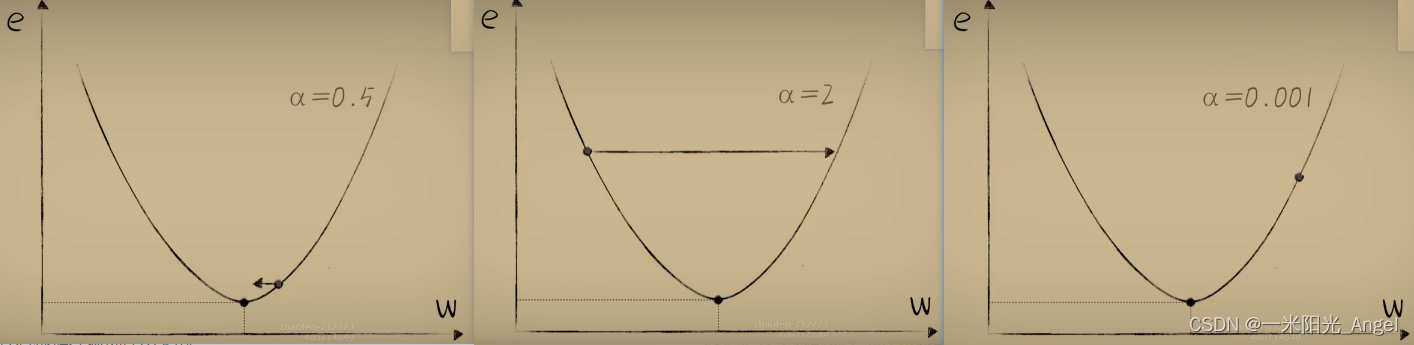
在调整过程中用来调和下降幅度的α 称之为 “学习率”，它的选择影响着调整的速度。
太大了，会容易反复横跳；
过大的时候甚至不会收敛而发散；
太小的话，又会磨磨唧唧
它是设计者根据经验选择出来的。

不断的经历前向传播和反向传播，最后到达代价函数最低点的过程，我们称之为“训练”或者“学习”。

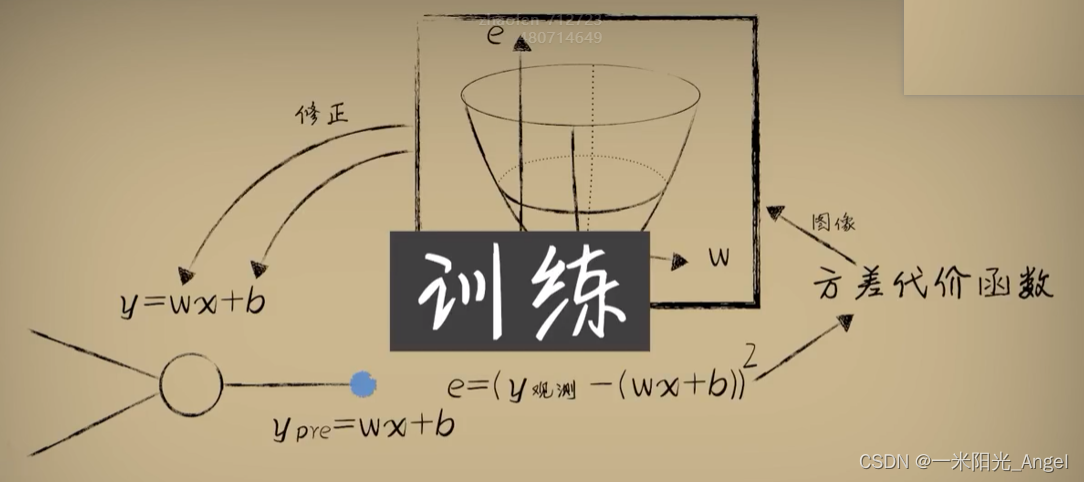
这就是 所谓 机器学习中的神经网络
但把一个神经元称之为“网络”似乎不太恰当，因为没有哪一个网络只有一个节点

但以后，我们不断的添加神经元，并将它们连接起来共同工作的时候，也就能称之为“神经网络”

而我们所说的“前向传播”和“反向传播”，也是在多层神经网络出现后，才引入的概念
对于单个神经元，如此称呼似乎有点别扭
但这些概念，在单个神经元上已经出备雏形。
面对网络，那只是不断重复而已。
会在多层神经网络中详细的说明“反向传播”的一般行为。