power method法求对称矩阵的主特征值+高斯消元法来一个LU分解+奇异值分解的一道题

本文链接：https://blog.csdn.net/zhoutianzi12/article/details/111373193

博客主要介绍了用power method法求对称矩阵的主特征值，使用高斯消元法进行LU分解，包括Doolittle分解和Crout分解，还给出奇异值分解的一道题，详细说明了求解U和V的过程，最后提到要检测计算结果是否正确。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

power method法求对称矩阵的主特征值
高斯消元法来一个LU分解
奇异值分解的一道题
- 检测做的对不对！

power method法求对称矩阵的主特征值

在这里插入图片描述

clear    
A=[1 1 3 4; 1 5 2 -1; 3 2 7 4; 4 -1 4 6];
x0 = [1;0;0;0];
for i = 1:10
    disp(x0)
    disp((A*x0)'* x0)
    x1 = (A*x0)/norm(A*x0);
    x0 =x1;
end

高斯消元法来一个LU分解

用高斯直接可以得到Doolittle分解

>> L=[1 0 0 0 ;-3 1 0 0; 2 4 1 0; 0 6 -7 1]

L =

     1     0     0     0
    -3     1     0     0
     2     4     1     0
     0     6    -7     1

>> U =[2 -2 4 -4 ; 0 -3 -9 6;0 0 1 8 ; 0 0 0 4]

U =

     2    -2     4    -4
     0    -3    -9     6
     0     0     1     8
     0     0     0     4

>> L*U

ans =

     2    -2     4    -4
    -6     3   -21    18
     4   -16   -27    24
     0   -18   -61   -16

>>

还需要变一下才能得到Crout分解

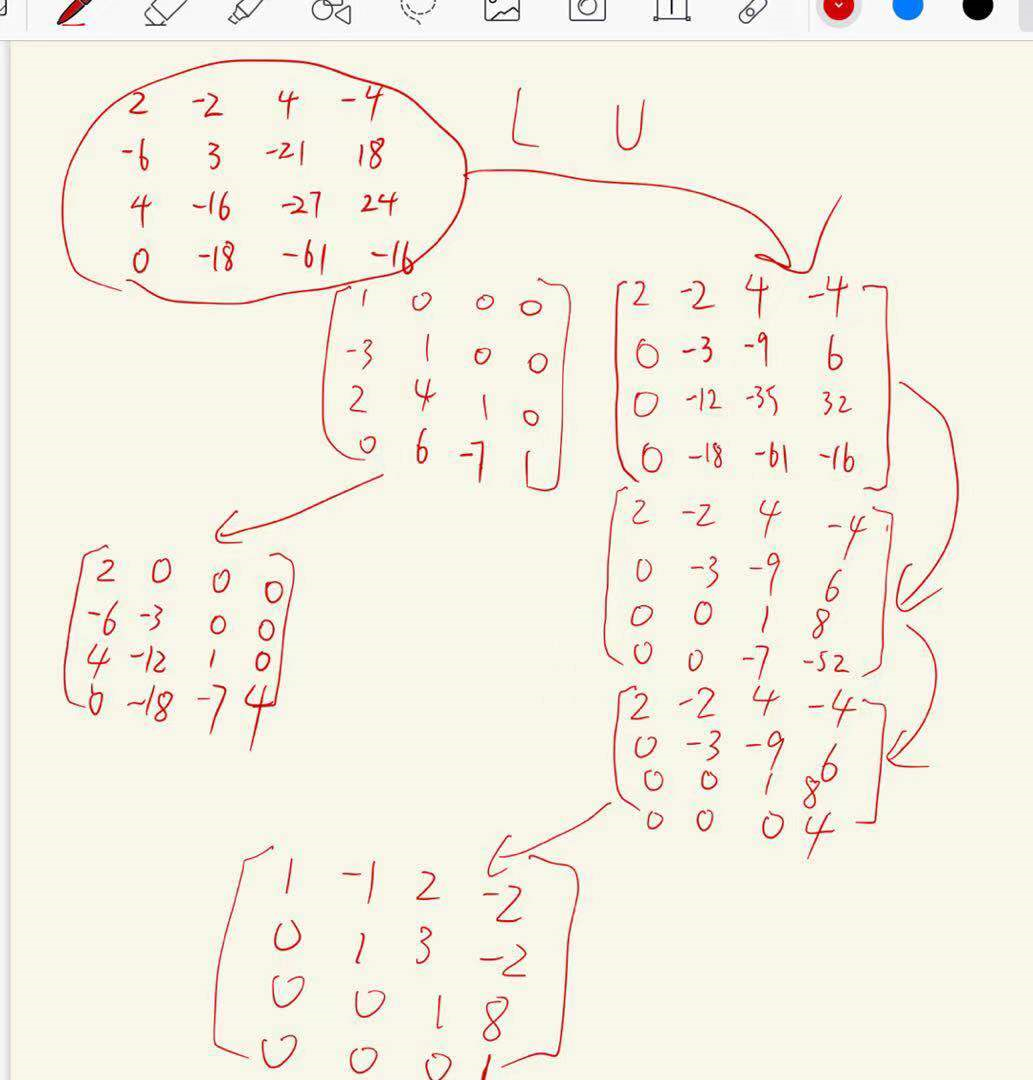
>> L=[2 0 0 0 ; -6 -3 0 0 ; 4 -12 1 0;0 -18 -7 4]

L =

     2     0     0     0
    -6    -3     0     0
     4   -12     1     0
     0   -18    -7     4

>> U=[1 -1 2 -2; 0 1 3 -2; 0 0 1 8; 0 0 0 1]

U =

     1    -1     2    -2
     0     1     3    -2
     0     0     1     8
     0     0     0     1

>> L*U

ans =

     2    -2     4    -4
    -6     3   -21    18
     4   -16   -27    24
     0   -18   -61   -16

奇异值分解的一道题

$A=U\Sigma V^T$

我先用

A=[36    -6     6;2    13    22;22    38   -13; 4    26    44]
[X,B] =eig(A'*A)

算出了 $V$ 的每一列！
- 隐藏在X变量的每一列

>> [X,B] =eig(A'*A)

X =

   -0.6667   -0.6667    0.3333
    0.6667   -0.3333    0.6667
   -0.3333    0.6667    0.6667


B =

   1.0e+03 *

    1.1250         0         0
         0    2.0250         0
         0         0    3.6000

然后求出了U的三列！
必须用这种方法去求！
记得标准化哦！

>> A*X(:,1)

ans =

  -30.0000
   -0.0000
   15.0000
   -0.0000

>> A*X(:,2)

ans =

  -18.0000
    9.0000
  -36.0000
   18.0000

>> A*X(:,3)

ans =

   12.0000
   24.0000
   24.0000
   48.0000

最后求得U的0对应的特征向量！

[X,B] =eig(A*A')

A =

    36    -6     6
     2    13    22
    22    38   -13
     4    26    44


X =

   -0.0000    0.8944    0.4000   -0.2000
   -0.8944   -0.0000   -0.2000   -0.4000
   -0.0000   -0.4472    0.8000   -0.4000
    0.4472         0   -0.4000   -0.8000


B =

   1.0e+03 *

   -0.0000         0         0         0
         0    1.1250         0         0
         0         0    2.0250         0
         0         0         0    3.6000

检测做的对不对！

    U=[1/5 -2/5    -2/sqrt(5)    0; 
       2/5  1/5      0        2/sqrt(5); 
       2/5  -4/5    1/sqrt(5)    0; 
       4/5   2/5       0    -1/sqrt(5)]

  
   V =[1/3 -2/3  -2/3; 
       2/3 -1/3  2/3; 
       2/3 2/3   -1/3]
    sigma = [60 0 0 ;0 45 0  ; 0 0 sqrt(1125) ; 0 0 0 ]
    
    U*sigma*V'