8线排

• 已介绍能在$O(nlogn)$时间内排序$n$个数的算法。
  • 归排和堆排达到了最坏情况下的上界
    • 快排在平均情况下达到该上界
• 且对这些算法中的每一个，我们都能给出$n$个输人数值，
• 使该算法能在$\Omega (nlgn)$时间内完成

 

• 这些算法都有一有趣性质：
  • 在排序最终结果中
  • 各元素的次序依赖于它们之间的比较。
  • 称比较排序，到目前，介绍的所有排序算法都是比较排序。

 

• 8.1证明对$n$个元素的输入序列来说，任何比较排序在最坏情况下都要经过$n(nlgn)$次比较。
  • so归排和堆排是渐近最优的，
  • 且任何已知的比较排序最多在常数因子上优于它们。
• 8.2、 8.3、8.4讨论三种线性时复的排序算法:
  • 计排、基排和桶排。
  • 这些是用运算而不是比较来确定排序顺序的。
  • 下界$O(nlgn)$对它们是不适用

8.1排序算法的下界

• 在比排中，只用元素间比较来获得输入序列$<a_1,...,a_n>$间次序
• 给$a_i$和$a_j$,，可执行$a_i<a_j等$ 5个中的一个比较来定它们间相对次序
  • 不能用其他方法观察元素的值
  • 或者它们之间的次序信息
• 不失一般性，本节中，不妨设所有的输人互异。
• 给定了这个假设后，$a=a$的比较就没意义。
  • 因此，可假设不要这种比较。
• 注意到$a_i\le a_j、a_i\ge a_j,、a_i>a_j和a_i<a_j$等价，
  • 因为通过它们所得到的关于$a_i$和$a_j$的次序的信息是相同的。
  • 这样，又可设所有比较采用的都是$a_i\le a_j$

决策树模型

• 比排可抽象为棵决策树。
  • 决策树是完二叉树，
  • 它可表示在给定输入规模情况下，某一特定排序算法对所有元素的比较操作。
  • 其中，控制、数据移动等其他操作都被忽略了。
  • 图8-1显示了2.1节中插人排序算法作用于包含三个元素的输人序列的决策树情况。

图8-1

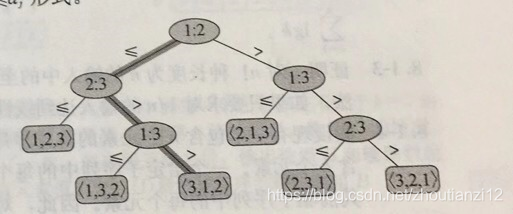
• 3元素时的插排决策树
• 标为$i:j$的内部结点表示$a_i$和$a_j$之间比较
• 排列为$<\pi (1),\pi (2),.\pi (n))$的叶结点
  • 表示得到的顺序$a_{\pi (1)}\le a_{\pi (2)}\le ...\le a_{\pi (n)}$
• 加阴影的路表示在对输人序列685排序时所做的决策
  • 叶结点上的<3, 1, 2>表示排序的结果$5\le 6\le 8$
  • 对输人来说，共有3! =6种可能的排列，因此决策树至少6叶子

第二段

• 决策树中，内部结点都以$i:j$标记，其中，$i$和$j$满足$1\le i,j\le n$, $n$是输人序列中的元素个数。
• 每个叶结点上都标注-个序列$<\pi (1),\pi (2),.\pi (n))$(序列的相关背景知识参阅C1节)。
• 排序算法的执行对应于一条从树的根结点到叶结点的路径。
• 每一个内部结点表示一次比较$a_i\le a_j$。
• 左子树表示一旦我们确定$a_i\le a_j$之后的后续比较，
• 右子树则表示在确定了$a_i>a_j$后的后续比较。
• 当到达一个叶结点时，表示排序算法已经确定了一个排序
  • $a_{\pi (1)}\le a_{\pi (2)}\le ...\le a_{\pi (n)}$

最坏情况的下界

8.2计算排序

• 若$n$个输入都是0到$k$一个整数
  • $k$是某个整数
  • 当$k=O(n)$时，排序的运行时间为$\Theta (n)$

计排的基本思想

• 计排的基本思想是：
  • 对输入$x$
  • 确定$<x$的元素个数
• 如有17个元素小于$x$
• 则$x$应该在第$18$个输出位置上
• 当有元素相同时，方案修改下。

计排的代码

• 算法输入是$A[1..n]，A.length=n$
• 还需
  • $B[1..n]$存放排序输出
  • $C[0..k]$提供临时存储空间
• COUNT-SORT(A,B,k)

let C[0..k] be a new array
for i=0 to k
	C[i]=0
for j=1 to A.length
	C[A[j]]=C[A[j]]+1
//C[i] now contains the number of elements equal to i
for i=1 to k
	C[i]=C[i]+C[i-1]
//C[i] onw conatins the number of elements less than or equal to i.
for j=A.length down to 1
	B[C[A[j]]]=A[j]
	C[A[j]]=C[A[j]]-1

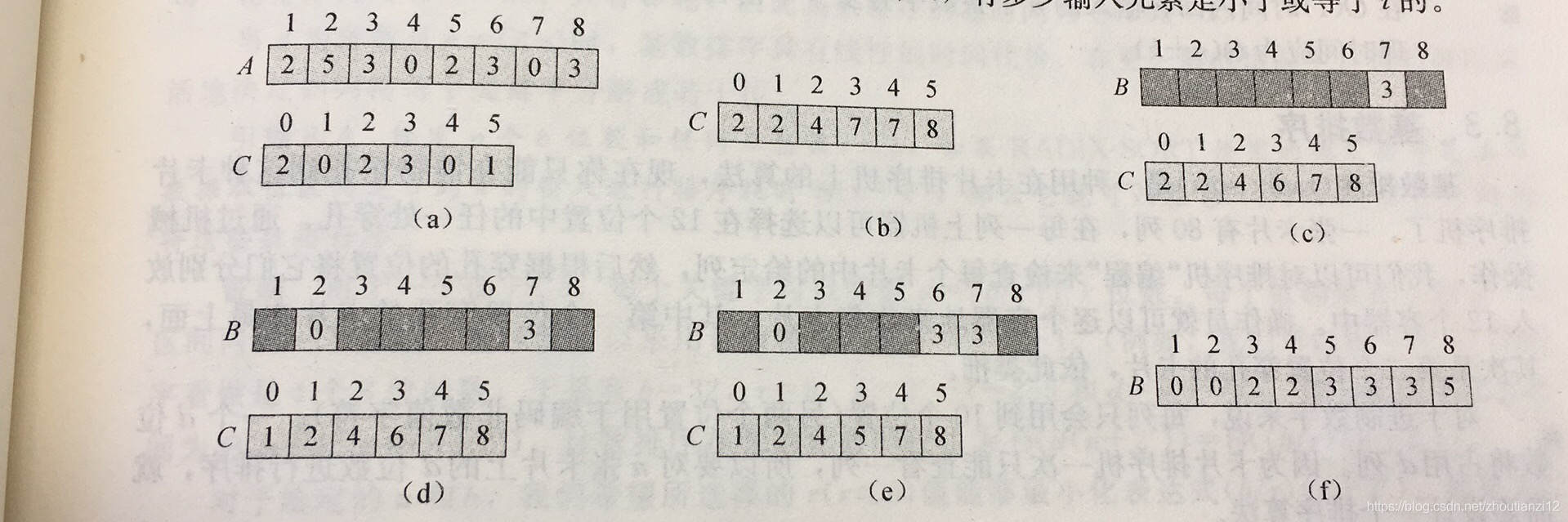
• 图8-2展示计排的运行过程
• 2-3行后，C均为0
• 4-5行遍历每个输入，如果为$i$，就把$C[i]加1$
• 5行完后，$C[i]$保存的是$=i$的元素个数$i=0...k$
• 7-8行加总计数对每一个$i=0..k$
  • 有多少元素$\le i$的
• 10-12行的for循环里
  • 把A[j]放到他在B中正确位置
  • 如果输入不同，那么第一次执行10行时，
    • 对每个$A[j]$值来说
    • $C[A[j]]$就是$A[j]$在输出数组中最终位置
    • 这是因为共有$C[A[j]]$个元素$\le$ $A[j]$
  • 若可能不互异，so每将 A[j]放到他在B中正确位置后
    • 都要将$C[A[j]]$减一
    • 这样遇到下一个等于$A[j]$的输入元素时，该元素可直接放到输出数组中$A[j]$前一位置

图8-2

• A中元素不大于$k=5$的
• (a)：第五行执行后的A和C
• (b)：第八行执行后,C的情况
• c到(e)：10-12行迭代1次,2次，3次
  • 其中B只有浅色部分有元素
• f最终结果

计数排序时间代价多少呢？

• 2-3行$\Theta (k)$
• 4-5$\Theta (n)$
• 7-8$\Theta (k)$
• 10-12$\Theta (n)$
• 总代价$\Theta (k+n)$
• 实际中
  • 当$k=O(n)$时
  • 用计排
  • 运时$\Theta (n)$

总结

• 下界优于
  • 因为他不是比较排序算法
  • 他的代码没有比较操作
  • 计数排序 是用输入元素实际值
  • 来确定其在数组中的位置
• 稳定的
• 通常稳定只有在当进行排序的数据还附带卫星数据时才重要
• 计排稳定性另一原因是
  • 它常被用作基排的一个子过程
• 下一节将看到
  • 为使基排正确运行
  • 计排必须是稳定的

8.3基数排序

8.4桶排序

• bucket sort
• 假设数据服从均匀,平均情况为O(n)
• 与计排类似,因为对输入作某种假设,桶排速度也很快
• 计排设输入都属于一个小区间内整数
• 桶排设输入是由一个随机过程产生,
  • 该过程将元素均匀、独立地分布在[0,1)区间
  • (C.2均匀分布定义)

 

• 桶排序将[0,1)划为n个相同大小子区间,称桶
• 将n输入数分别放到各桶
• 输入数据是均匀、独立地分布在[0,1)
• 一般不会出现很多数落在同一个桶中的情况。
• 为得到输出,先对每个桶中的数排序
  • 然后遍历每个桶,按次序把各个桶中的元素列出来

 

• 桶排
• 设输入是包含n个元素的数组A,
• 每个元素0≤A<1。
• 算法还要一个临时数组B[O.n-1]来存放链表(即桶),
  • 并假设存在一种维护这些链表的机制
  • (10.2节介绍如何实现链表的一些基本操作)