偏差方差分解——Bias-Variance Decomposition:
expected loss = bias2 + variance + noise
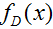
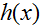
Expected loss of regression:
先看最右边的式子,
再看最左边的式子
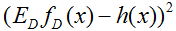
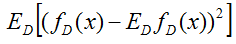
综上,我们得到了期望损失的偏差方差分解,
最右端项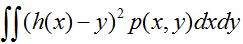
偏差方差分解——Bias-Variance Decomposition:
expected loss = bias2 + variance + noise
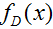
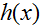
Expected loss of regression:
先看最右边的式子,
再看最左边的式子
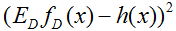
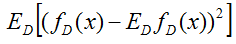
综上,我们得到了期望损失的偏差方差分解,
最右端项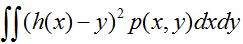











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


