Python实现行业轮动量化选股【附完整源码】

最新推荐文章于 2025-03-08 12:15:00 发布

小壁虎的春天

最新推荐文章于 2025-03-08 12:15:00 发布

阅读量1.9w

点赞数 19

分类专栏：量化交易文章标签：人工智能

原文链接：https://mp.weixin.qq.com/s?src=11&timestamp=1585105706&ver=2237&signature=3FegNyX2OewUe4jZmcUqlOz7qHwG7Lk8qT9GdKpoj-drIwTLXwE8xvXh*eLeEuAKz98XLk8VYaD1CgA18fFyvu9srsKCA3oIyFtO*oZ0KtAlapAfABKavqg9WrSMCViA&new=1

版权

量化交易专栏收录该内容

338 篇文章

订阅专栏

编者荐语：

所谓山不转水转，行业中的动量也存在一定的轮换效应。今天给大家分享一篇来自《量化小白上分记》的研报复现文章，基于因子动量、波动率、偏度、峰度来刻画行业轮动，对于构建行业轮动量化选股具有一定的参考价值。

以下文章来源于量化小白上分记，作者量化小白H

本文主要参考了报告[1]，报告数据代码获取后台回复“高阶矩行业轮动”。

1.背景

大量研究表明，A股行业有明显的轮动现象，并且与A股相反，行业指数通常呈现动量特征，即前期涨幅高的行业，会延续上涨的趋势，比前期涨幅低的行业有明显超额收益。

此外，也有大量研究表明，A股市场存在明显的低波动异象，即前期波动率更低的行业，相比于波动率高的行业，未来有明显超额收益。因为投资者不愿意承担过高的风险。这一现象在行业上也是显著存在的。本文参考报告[1]中对波动率因子的定义，对行业上的波动因子进行测试。

最后，考虑到动量是收益率的一阶矩，波动率是收益率的二阶矩，自然而然的想到，是否收益率的三阶矩、四阶矩是否也能对行业的轮动现象做出解释。即用偏度、峰度作为因子做行业轮动。这两个因子也有一些文献做过研究。偏度反映的是数据整体相较于均值的偏离的程度，正偏度越高，表明整体高于均值的程度更高，数据右拖尾。负偏度越高，表明数据整体低于均值的程度更高，数据左拖尾，总体来说，偏度的绝对值越大，表明数据出现极端值的情况越多。峰度则反映数据整体的集中程度，集中程度越高，峰度越高。

综上，本文通过因子的动量、波动率、偏度、峰度进行行业轮动测试。

2. 因子定义

动量因子：行业过去20天收益率累计
波动率因子：参考报告[1]的VOL定义，具体如下

偏度因子：用上文高低价计算的rHL计算偏度作为偏度因子
峰度因子：用今开昨收计算的收益率计算峰度作为峰度因子

具体行业轮动策略如下

回测区间：2006.01-2019.06
频率：月度
标的：中信一级行业指数
评价方法：因子IC，ICIR，分层测试曲线，FamaMacBeth回归，因子合成

3. 回测结果

因子累计IC曲线如下：

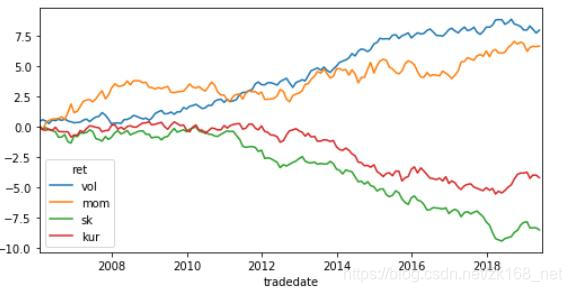
其中，mom为动量因子，vol为波动率因子，sk为偏度因子，kur为峰度因子。IC均值、年化ICIR如下：

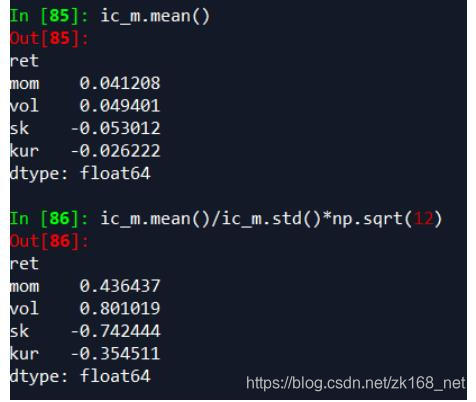
可以看出，月度上偏度因子、波动率因子比较有效，稳定性较高，动量因子ic较高，但稳定性较差，峰度因子一般。

四个因子的分层测试曲线如下：

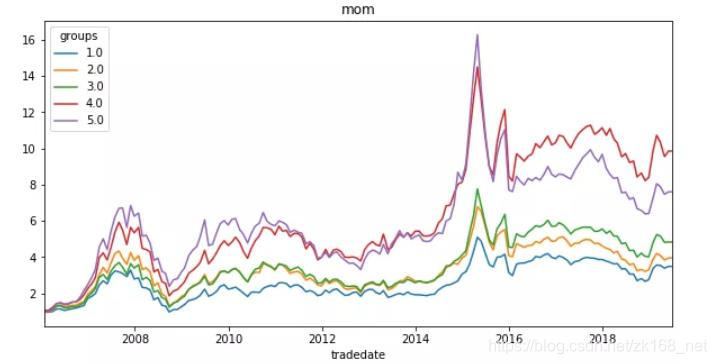
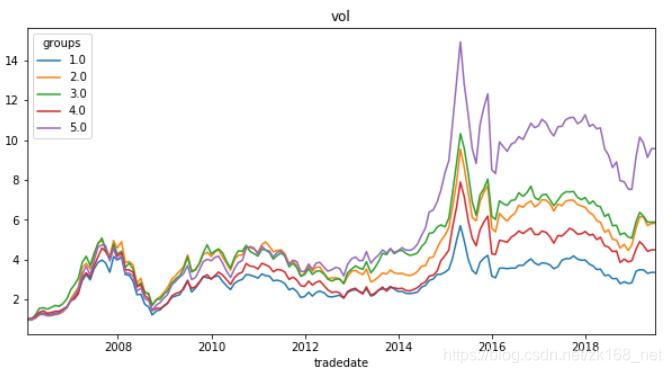
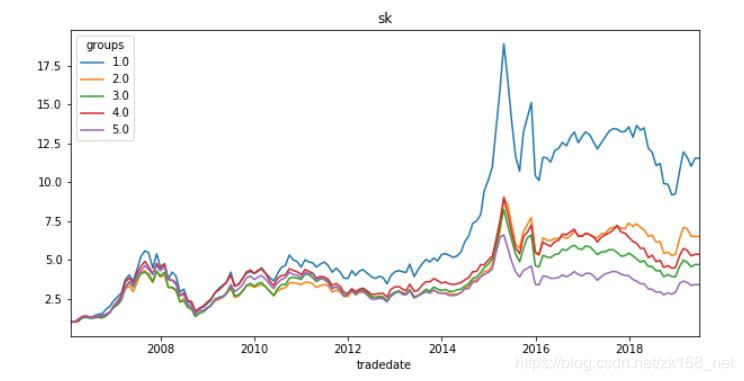
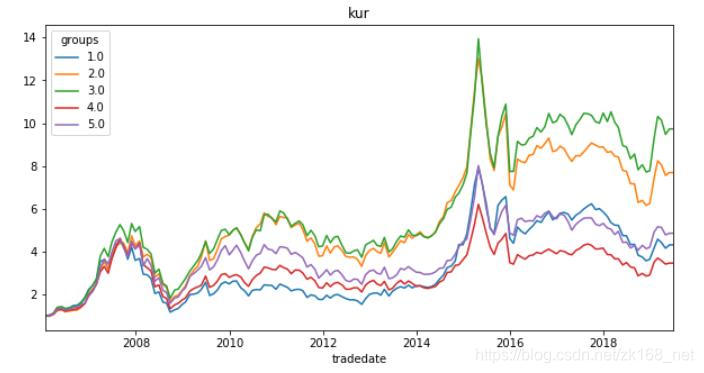
可以看出，波动率因子、偏度因子的分层特性非常好，Top组明显优于其他组。

各因子的Spearman相关性矩阵如下：

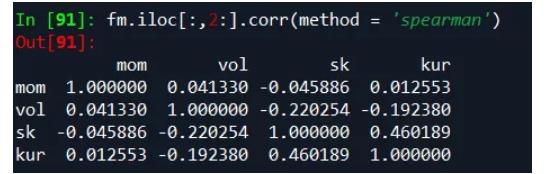
偏度和峰度的相关性较高，偏度和波动率的相关性较高。其他各因子之间的相关性都很低。

接下来用FamaMacBeth回归来看在动量因子和波动率因子的基础上，偏度、峰度因子是否能提供额外的信息。FamaMacBeth回归的原理和代码实现参考上一篇《Fama-Macbeth回归和Newey-West调整》。

首先用动量和波动率因子做回归，结果如下，需要注意的位置已标红

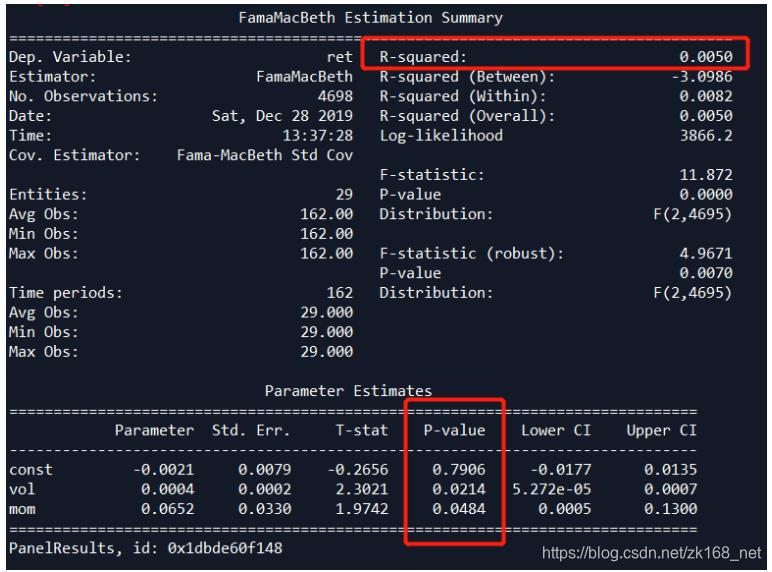
再加入偏度因子回归

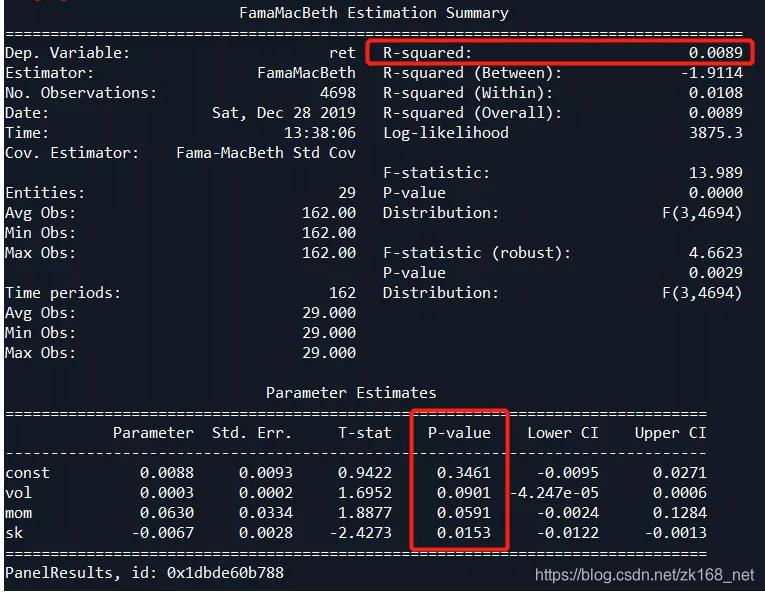
再用动量、波动率、峰度回归

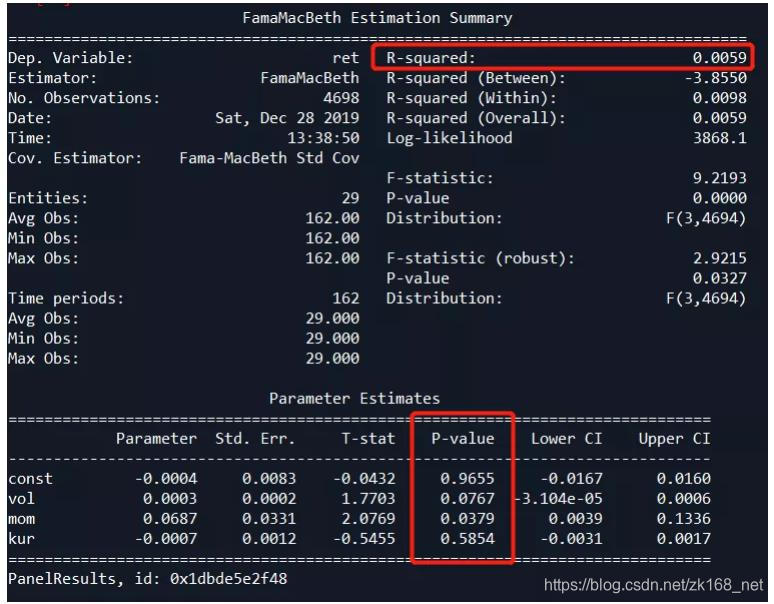
最后用四个因子一起回归

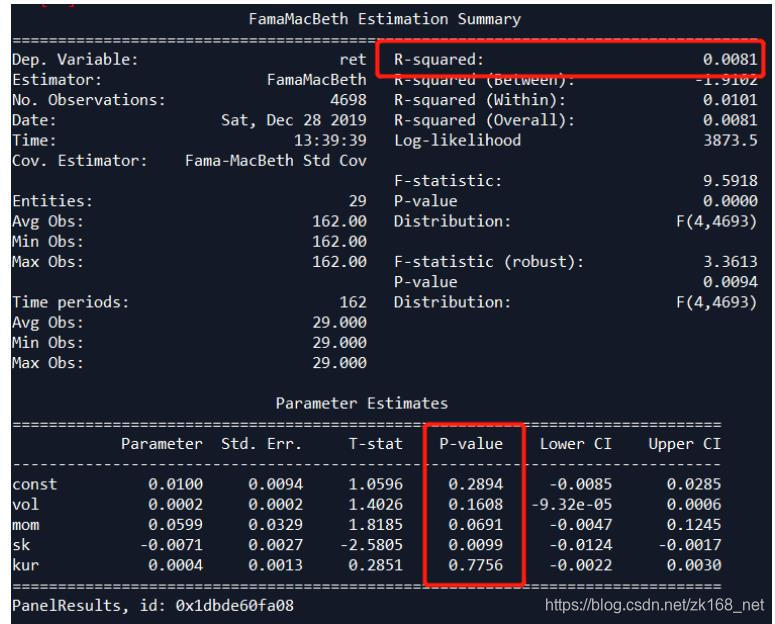
结果如果做一个表格的话，会看的更清楚一些，这里我就直接用图解释了：

首先动量因子、波动率因子都是5%显著的，只加入偏度的话，两个因子都在10%上显著，偏度在5%上显著，波动率的显著性降低较多，说明偏度包含的信息与波动率重复较多，但也有额外信息。此外模型的R2也有明显提升，说明加入偏度是有提升的，因子的方向也与前面IC方向一致。
只加入峰度的话，两因子在10%上显著，峰度不显著，并且模型R2基本没有变，说明峰度没有额外信息。
如果四个因子都包括的话，峰度不显著，波动率不显著，R2显著提升，这都可以用以上两点的结论来解释。
综上，偏度因子比较有效，峰度因子有效性不高，最后用动量、波动率、偏度因子做等权合成f1，f1的IC、ICIR、分层曲线如下

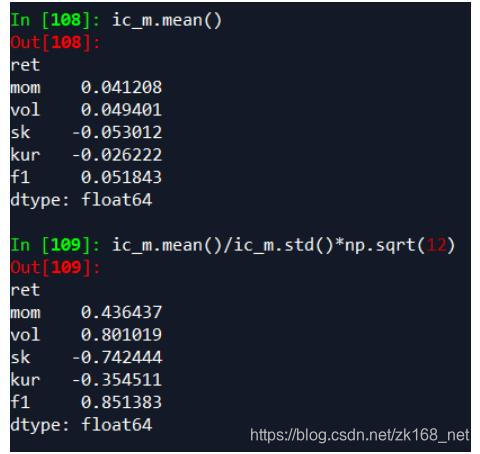
合成之后，因子稳定性显著提升，分层曲线如下：

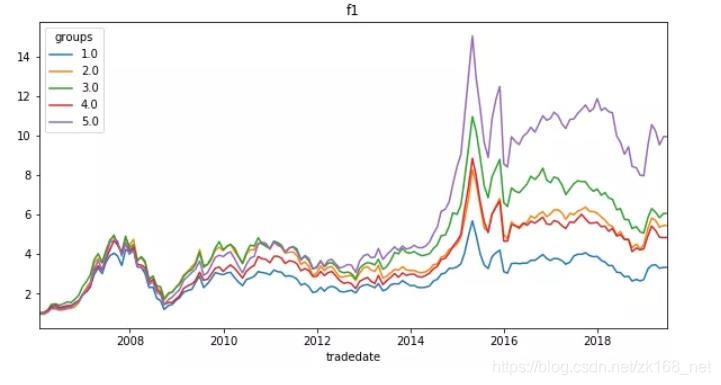
最后需要说明，量价类的因子在周度上比月度更为有效，周度上峰度、偏度都是有效的，并且相关性不高。限于篇幅，这里不给出周度的结果,有兴趣自己测试一下。

4.代码

import os
import pandas as pd
import numpy as np
import datetime
from linearmodels import FamaMacBeth
import statsmodels.api as sm

def getRet(price,freq ='d',if_shift = True):
    price = price.copy()
   
    if freq == 'w':
        price['weeks'] = price['tradedate'].apply(lambda x:x.isocalendar()[0]*100 + x.isocalendar()[1])
        ret = price.groupby(['weeks','classname']).last().reset_index()
        del ret['weeks']
    
    elif freq =='m':
        price['ym'] = price.tradedate.apply(lambda x:x.year*100 + x.month)
        ret = price.groupby(['ym','classname']).last().reset_index()
        del ret['ym']
    
    ret = ret[['tradedate','classname','s_dq_close']]
    if if_shift:
        ret = ret.groupby('classname').apply(lambda x:x.set_index('tradedate').s_dq_close.pct_change(1).shift(-1))
    else:
        ret = ret.groupby('classname').apply(lambda x:x.set_index('tradedate').s_dq_close.pct_change(1))
    
    ret = ret.T.stack(dropna = False).reset_index()
    ret = ret.rename(columns = {ret.columns[2]:'ret'})
    return ret

def getdate(x):
    if type(x) == str:
        return pd.Timestamp(x).date()
    else:
        return datetime.date(int(str(x)[:4]),int(str(x)[4:6]),int(str(x)[6:]))
# 隔夜收益率
def ret_after_days(x):
    x = x.set_index('tradedate')
    r = x.s_dq_open/x.s_dq_close.shift(1) - 1
    return r
def GroupTestAllFactors(factors,ret,groups):
    """
    一次性测试多个因子
    """
    fnames = factors.columns
    fall = pd.merge(factors,ret,left_on = ['classname','tradedate'],right_on = ['classname','tradedate'])
    Groupret = []
    Groupic = []
    for f in fnames: # f= fnames[2]
        if ((f != 'classname')&(f != 'tradedate')):
            fuse = fall[['classname','tradedate','ret',f]]
        
            fuse['groups'] = fuse[f].groupby(fuse.tradedate).apply(lambda x:np.ceil(x.rank()/(len(x)/groups)))
            result = fuse.groupby(['tradedate','groups']).apply(lambda x:x.ret.mean())
            result = result.unstack().reset_index()
            result.insert(0,'factor',f)
            Groupret.append(result)
            groupic = fuse.groupby(['tradedate','groups']).apply(lambda x:x.corr(method = 'spearman').values[0,1])
            groupic = pd.DataFrame(groupic,columns = [f])
            groupic = groupic.reset_index().pivot(index = 'tradedate',columns = 'groups',values = f)
            groupic.insert(0,'factor',f)
            Groupic.append(groupic)
# print(f)
    Groupret = pd.concat(Groupret,axis = 0).reset_index(drop = True)
    Groupret = Groupret.fillna(0)
    Groupnav = Groupret.iloc[:,2:].groupby(Groupret.factor).apply(lambda x:(1 + x).cumprod())
    Groupnav = pd.concat([Groupret[['tradedate','factor']],Groupnav],axis = 1)

    Groupic = pd.concat(Groupic,axis = 0)
    return Groupnav,Groupic
def getICSeries(factors,ret,method):
    # method = 'spearman';factors = fall.copy();

    icall = pd.DataFrame()
    fall = pd.merge(factors,ret,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])
    icall = fall.groupby('tradedate').apply(lambda x:x.corr(method = method)['ret']).reset_index()
    icall = icall.drop(['ret'],axis = 1).set_index('tradedate')

    return icall

'''
数据读入
'''
datas = pd.read_csv('中信一级行业指数日度行情序列.csv',encoding = 'gbk')
#datas = pd.read_csv('申万一级行业指数日度行情序列.csv',encoding = 'gbk')

'''
收益率计算
'''
# 当日和前一日收盘价算的收益率
ret = datas.groupby('classname').apply(lambda x:x.set_index('tradedate').s_dq_close.pct_change(1)).T.stack(dropna = False).reset_index()
ret = ret.rename(columns = {ret.columns[2]:'ret'})
ret['tradedate'] = ret.tradedate.apply(getdate)

# 开收盘价算的收益率
ret_oc = datas.groupby('classname').apply(lambda x:x.set_index('tradedate').s_dq_close/x.set_index('tradedate').s_dq_open - 1).T.stack(dropna = False).reset_index()
ret_oc = ret_oc.rename(columns = {ret_oc.columns[2]:'ret'})
ret_oc['tradedate'] = ret_oc.tradedate.apply(getdate)

# 高低价算的收益率
ret_hl = datas.groupby('classname').apply(lambda x:(x.set_index('tradedate').s_dq_high - x.set_index('tradedate').s_dq_low)/(x.set_index('tradedate').s_dq_high + x.set_index('tradedate').s_dq_low)/2).T.stack(dropna = False).reset_index()
ret_hl = ret_hl.rename(columns = {ret_hl.columns[2]:'ret'})
ret_hl['tradedate'] = ret_hl.tradedate.apply(getdate)

# 正常的逐日收益率计算
datas['tradedate'] = datas.tradedate.apply(getdate)
ret_m = getRet(datas,freq ='m',if_shift = True)

'''
因子计算
1. 动量因子：过去一个月/周的涨跌幅
2. 波动率因子：过去一个月/周的日收益率的波动率
收益率1 ：开/收 - 1
收益率2：（高 - 低）/（高 + 低）/2
波动率因子 = 波动率因子1和2打分后加总
3. 偏度因子 ：收益率的偏度
4. 峰度因子：波动率的峰度

'''
N = 20
# 1月动量
mom_m = ret.groupby('classname').apply(lambda x:x.set_index('tradedate').rolling(15).sum()).fillna(0)
mom_m = mom_m.reset_index()
mom_m = mom_m.rename(columns = {mom_m.columns[2]:'mom'})
 
# 波动率因子
vol_m_1 = ret_oc.groupby('classname').apply(lambda x:x.set_index('tradedate').rolling(N).std()).fillna(0)

vol_m_1 = vol_m_1.reset_index()
vol_m_1 = vol_m_1.rename(columns = {vol_m_1.columns[2]:'vol_m_1'})

vol_m_2 = ret_hl.groupby('classname').apply(lambda x:x.set_index('tradedate').rolling(N).std()).fillna(0)
vol_m_2 = vol_m_2.reset_index()
vol_m_2 = vol_m_2.rename(columns = {vol_m_2.columns[2]:'vol_m_2'})
 
# 偏度因子
sk = ret_hl.groupby('classname').apply(lambda x:x.set_index('tradedate').rolling(N).skew()).fillna(0)
sk = sk.reset_index()
sk = sk.rename(columns = {sk.columns[2]:'sk'})
 
# 峰度因子
kur = ret.groupby('classname').apply(lambda x:x.set_index('tradedate').rolling(N).kurt()).fillna(0)
kur = kur.reset_index()
kur = kur.rename(columns = {kur.columns[2]:'kur'})

# 峰度因子
"""
因子合并
"""
factors_m = pd.merge(mom_m,vol_m_1,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])
factors_m = pd.merge(factors_m,vol_m_2,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])
factors_m['vol'] = factors_m.vol_m_1.groupby(factors_m.tradedate).rank(ascending = True) + factors_m.vol_m_2.groupby(factors_m.tradedate).rank(ascending = False)
factors_m = pd.merge(factors_m,sk,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])
factors_m = pd.merge(factors_m,kur,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])

factors_m = factors_m.drop(['vol_m_1','vol_m_2'],axis = 1)
# factors_m['r1'] = factors_m.vol_m_1.groupby(factors_m.tradedate).rank(ascending = False)

"""
因子测试
"""
groups = 5

startdate = datetime.date(2006,1,1)
enddate = datetime.date(2019,6,30)

fm = factors_m.loc[(factors_m.tradedate>= startdate) &(factors_m.tradedate <= enddate)].reset_index(drop = True).copy()

fm['f1'] = fm['vol'] + fm['mom']
fm['f2'] = fm['vol'] + fm['mom'] - fm['sk'] -fm['kur']

# IC
ic_m = getICSeries(fm,ret_m,'spearman')

ic_m[['vol','mom','sk','kur']].cumsum().plot(figsize = (8,4))
ic_m.mean()
ic_m.mean()/ic_m.std()*np.sqrt(12)

fm.iloc[:,2:].corr(method = 'spearman')

nav_m,ic_m = GroupTestAllFactors(fm,ret_m,groups)

nav_m.loc[nav_m.factor == 'mom'].set_index('tradedate').plot(figsize = (10,5),title = 'mom')
nav_m.loc[nav_m.factor == 'vol'].set_index('tradedate').plot(figsize = (10,5),title = 'vol')
nav_m.loc[nav_m.factor == 'sk'].set_index('tradedate').plot(figsize = (10,5),title = 'sk')
nav_m.loc[nav_m.factor == 'kur'].set_index('tradedate').plot(figsize = (10,5),title = 'kur')
nav_m.loc[nav_m.factor == 'f1'].set_index('tradedate').plot(figsize = (10,5),title = 'f1')
nav_m.loc[nav_m.factor == 'f2'].set_index('tradedate').plot(figsize = (10,5),title = 'f2')

# FamaMacbeth

fall = pd.merge(fm,ret_m,left_on = ['tradedate','classname'],right_on = ['tradedate','classname'])
fall = fall.set_index(['classname','tradedate']).fillna(0)

fm = FamaMacBeth(dependent = fall['ret'],exog = sm.add_constant(fall[['vol','mom']]))
fm.fit()
 
fm = FamaMacBeth(dependent = fall['ret'],exog = sm.add_constant(fall[['vol','mom','sk']]))
fm.fit()
 
fm = FamaMacBeth(dependent = fall['ret'],exog = sm.add_constant(fall[['vol','mom','kur']]))
fm.fit()

fm = FamaMacBeth(dependent = fall['ret'],exog = sm.add_constant(fall[['vol','mom','sk','kur']]))
fm.fit()

参考文献

[1]20170409-海通证券-海通证券金融工程专题报告：动量策略及收益率高阶矩在行业轮动中的应用-388742

推荐阅读：

1.一个量化策略师的自白（好文强烈推荐）

2.股票期货经典的量化交易策略都在这里了！（源码）

3.期货/股票数据大全查询（历史/实时/Tick/财务等）

4.当真躺着赚钱？量化交易的十大难题

5.从量化到高频交易，不可不读的五本书

6.如何有效的规避量化交易中的滑点？