Datawhale组队学习2025.2数学建模导论 Task1 数据处理与拟合模型

笔者身为小白，希望得到您的指正，希望您在评论区告诉去我准备数学建模编程手和建模手的一些建议

1.1 什么是数据

• 数值类数据，例如结构化的excel表格和SQL文件。
• 文本类数据，例如新闻报道、微博评论、餐饮点评等文字。
• 图像类数据，以一定尺寸的黑白或彩色图像在计算机内存储。
• 音频类数据，例如音乐、电话录音等。
• 信号类数据，例如地震波的波形、电磁波信号、脑电信号等

SQL数据：关系型数据库的查询语句，数据库分为关系型数据库和非关系型数据库，数据分为结构化数据和非结构化数据，例如，一个有年龄，身高，体重，籍贯的Excel表是结构化数据，结构化的数据放在关系型数据库里，关系型数据库常见的有MySQL,Oracle,MySQL免费，而图片音频属于非结构化数据，属于NoSQL，储存在非结构化数据库中。能够在MySQL数据库中，使用SQL语言，将所需要的数据提取出来，就是掌握了SQL。

注意：视频数据为什么没有单列呢？因为视频本身也是由一帧帧图像在时间轴上堆叠才形成的数据。如果加上声音就更完美了。所以本质上视频数据是图像和音频的融合。

面对不同的数据，能够使用最合适的方法最为重要。而判断此方法是否合适，一个根本的衡量就是数据的体量。

csv、tsv等格式的数据可以用记事本、excel、WPS等打开

以下用到的数据在链接里

https://github.com/Git-Model/__init_Modeling__。

1.2.1 数据的预处理

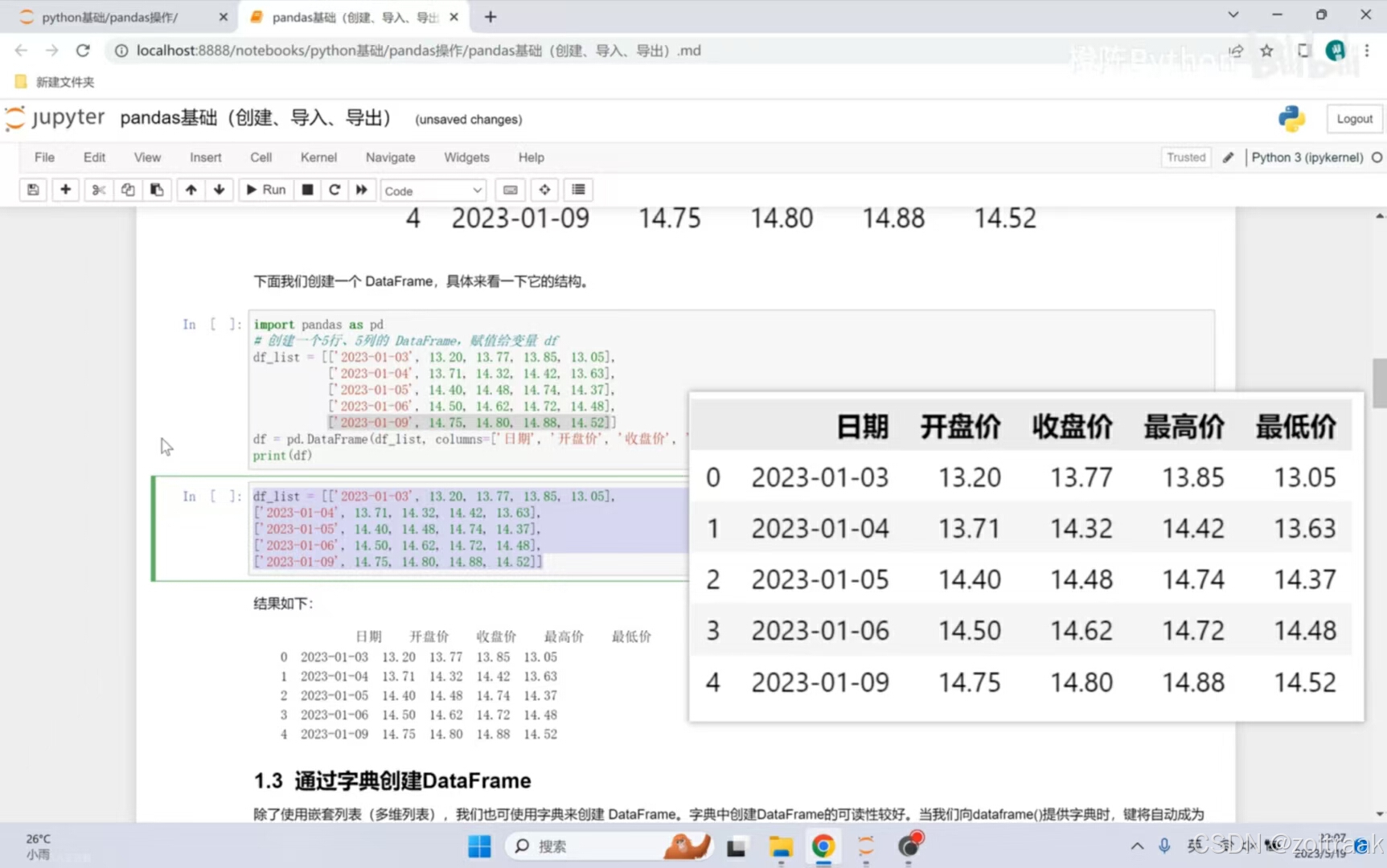
最上面一行我们称之为表头，表头的每一格我们称之为字段。数据的每一列称为属性，属性有离散和连续之分，目标客户编号提供了每一行数据的标识信息，可以根据这个编号对数据进行检索排序，称之为“主码”，也可以理解为id。

1.2.2 使用pandas处理数据的基础

  1 DataFrame数据结构

DataFrame是Python库中的一种数据结构，也称数据框，相当于Python中的Excel表格。DataFrame的单元格中可以存放数据，同时DataFrame可以设置列名columns和行名index。

在Pandas中使用pd.DataFrame()函数来创建DataFrame,通过参数Data传入数据，通过参数columns来指定数据框索引，通过参数index指定数据框行索引。

  pd.DataFrame(data,columns= [],index=[]

DataFrame支持通过列表，字典等数据类型创建。

例如：

图片中给出了一个嵌套的列表，pandas可以将嵌套列表转变为数据框结构，也可以通过columns设置行索引，通过index设置列索引

此外，还可以通过字典创建DataFrame,输入一系列的键值对，其优势是无需设置columns参数。

1.2.3 数据的规约

   因为实际应用中数据的分布可能是有偏的，量纲影响和数值差异可能会比较大。规约是为了形成对数据的更高效表示

  这里我们就介绍两个比较典型的规约方式：min-max规约和Z-score规约。

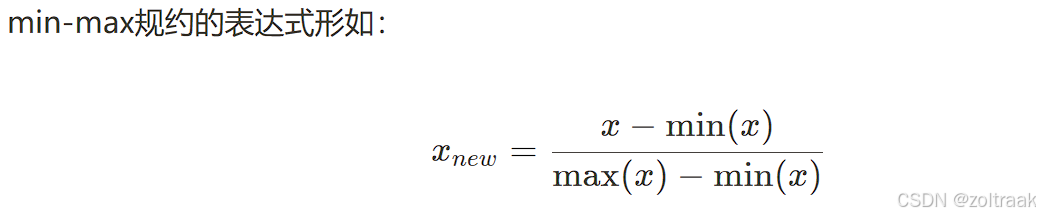
  如果出现非常大的值，这·个数据是有偏的，介绍Z-score规约

 本质上，一列数据减去其均值再除以标准差，如果这一列数据近似服从正态分布，这个过程就是化为标准正态分布的过程。Z-score规约和min-max规约往往不是二者取其一，有时候两个可以组合起来用。除此以外，还有很多的规约方法，但是这两种最为常用。

  2.1 数据导入

  2.1.1 Excel的数据导入

pandas读取和输出函数

文件格式	Pandas读取函数	Pandas输出函数
Excel	read_excel	to_excel
CSV,TXT	read_csv()	to_csv()
SQL查询数据库	read_sql()	to_sql()
DTA	read_stata()	to_stata()

在pandas库中，导入Excel文件使用的是，read_excel()方法，类似于excel打开文件，pandas读取文件将sheet中的数据后转化为DataFrame对象，DataFrame对象是有行索引和列索引,read_excel
函数有两个参数来对行列索引进行设置。

import pandas as pd
df = pd.read_excel(r"   ")# 绝对路径 raw
print ()

打开文件，右键，点击复制文件地址，即可得到。绝对路径和相对路径的区别：绝对路径是寄快递，相对路径是打车，绝对路径要求详细。默认将第一行列索引。

实例：例如，我将2024年美赛官方给出的数据包导入pandas。

import pandas as pd

# 读取CSV文件
df = pd.read_csv(r'C:\Users\王正智\OneDrive\Desktop\2025_Problem_C_Data\2025_Problem_C_Data\summerOly_medal_counts.csv')

# 查看前几行数据
print("前5行数据：")
print(df.head())

# 查看数据的基本信息
print("\n数据基本信息：")
print(df.info())

# 查看数据的统计信息
print("\n数据统计信息：")
print(df.describe())

    mean是均值，std是标准差

2.2 常见的统计分析模型

这里将介绍几种常用的统计分析的方法，由于统计分析的原理涉及大量数学知识，对这部分知识的原理感兴趣的话，欢迎查看：https://github.com/Git-Model/Modeling-Universe/tree/main/Data-Story

2.2.1回归分析和分类分析

回归分析与分类分析都是一种基于统计模型的统计分析方法。它们都研究因变量（被解释变量）与自变量（解释变量）之间存在的潜在关系，并通过统计模型的形式将这些潜在关系进行显式的表达。不同的是，回归分析中因变量是连续变量，如工资、销售额；而分类分析中因变量是属性变量，如判断邮件“是or否”为垃圾邮件。

以分析大学成绩GPA是否与入学成绩以及高考成绩有关为例

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns
from IPython.display import display
import statsmodels.api as sm

# 加载数据
gpa1=pd.read_stata('./data/gpa1.dta')

# 在数据集中提取自变量（ACT为入学考试成绩、hsGPA为高考成绩）
X1=gpa1.ACT
X2=gpa1[['ACT','hsGPA']]
# 提取因变量
y=gpa1.colGPA

# 为自变量增添截距项
X1=sm.add_constant(X1)
X2=sm.add_constant(X2)
display(X2)


# 拟合两个模型
gpa_lm1=sm.OLS(y,X1).fit()
gpa_lm2=sm.OLS(y,X2).fit()

# 输出两个模型的系数与对应p值
p1=pd.DataFrame(gpa_lm1.pvalues,columns=['pvalue'])
c1=pd.DataFrame(gpa_lm1.params,columns=['params'])
p2=pd.DataFrame(gpa_lm2.pvalues,columns=['pvalue'])
c2=pd.DataFrame(gpa_lm2.params,columns=['params'])
display(c1.join(p1,how='right'))
display(c2.join(p2,how='right'))

如果代码出不来是因为没下载数据，数剧在开头链接·

从模型I可以看到，ACT变量的pvalue为0.01<0.05，说明大学入学考试成绩ACT能显著影响大学GPA；但从模型II可以看到，高考成绩haGPA的pvalue为0.000005远小于0.05，说明高考成绩haGPA显著影响大学成绩GPA，但大学入学考试成绩ACT的pvalue为0.38大于0.05，不能说明大学入学考试成绩ACT显著影响大学成绩GPA。为什么会出现这样矛盾的结论呢？原因有可能是：在没有加入高考成绩haGPA时，大学入学考试成绩ACT确实能显著影响大学成绩GPA，但是加入高考成绩haGPA后，有可能高考成绩haGPA高的同学大学入学考试也高分，这两者的相关性较高，显得“大学入学考试成绩ACT并不是那么重要”了。

从模型II的系数params数值可以看到，当高考成绩haGPA显著影响大学成绩GPA，params为0.45代表每1单位的高考成绩的增加将导致大学GPA平均增加0.45个单位。

2）分类分析：ST是我国股市特有的一项保护投资者利于的决策，当上市公司因财务状况不佳导致投资者难以预测其前景时，交易所会标记该公司股票为ST，并进行一系列限制措施。我们想研究被ST的公司其背后的因素，并尝试通过利用公司的财务指标提前预测某上市公司在未来是否会被ST，是一件很有意义的举措。

# 加载基础包
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy import stats

# 读取数据
ST=pd.read_csv('./data/ST.csv')
ST.head()

st_logit=sm.formula.logit('ST~ARA+ASSET+ATO+ROA+GROWTH+LEV+SHARE',
data=ST).fit()
print(st_logit.summary())

 

在统计学和回归分析中，**p值（p-value）**是一个非常重要的概念，用于衡量某个变量对因变量的影响是否具有统计学意义。你的描述中提到的“P(>|z|)”是回归分析结果中常见的p值表示方式，通常用于线性回归或逻辑回归模型中。以下是对p值的详细解释，以及它在回归分析中的作用。

---

1. p值的含义

p值（p-value）是一个概率值，用于衡量观测数据与假设之间的矛盾程度。在回归分析中，p值用于检验某个自变量（解释变量）是否对因变量（被解释变量）有显著影响。

具体来说：

• 原假设（Null Hypothesis）：假设某个自变量对因变量没有显著影响，即该自变量的回归系数为0。

• 备择假设（Alternative Hypothesis）：假设某个自变量对因变量有显著影响，即该自变量的回归系数不为0。

p值表示在原假设成立的情况下，观测到当前数据（或更极端数据）的概率。换句话说，p值越小，说明观测数据与原假设之间的矛盾越大，原假设越不可信。

---

2. P(>|z|) 的含义

在回归分析中，尤其是逻辑回归（Logistic Regression）中，p值通常用“P(>|z|)”表示。这里的“z”是指z统计量，它是回归系数的标准化检验统计量。具体计算公式为：

z=标准误回归系数​

其中，回归系数是自变量对因变量的影响程度，标准误是回归系数的估计误差。

“P(>|z|)”表示在原假设成立的情况下，z统计量的绝对值大于或等于观测值的概率。如果这个概率很小（通常小于0.05），则认为原假设不成立，即该自变量对因变量有显著影响。

---

3. p值与显著性水平

在实际应用中，我们通常设定一个显著性水平（α），常用的显著性水平是0.05。根据p值与显著性水平的关系，可以得出以下结论：

• 如果 p值 < 0.05：拒绝原假设，认为该自变量对因变量有显著影响。

• 如果 p值 ≥ 0.05：无法拒绝原假设，认为该自变量对因变量没有显著影响。

2.2.2 假设的检验

  在数学建模中，我们既能通过假设检验对数据进行探索性的信息挖掘，以给予我们选择模型充分且客观的依据；又能在建模完成后，通过特定的假设检验验证模型的有效性。

我们要对某个命题进行真假判断，这个问题就是假设检验问题。

假设检验大体上可分为两种：参数假设检验与非参数假设检验。若假设是关于总体的一个参数或者参数的集合，则该假设检验就是参数假设检验，刚刚的例子的假设是关于总体均值的，均值是参数，因此这是一个参数假设检验；若假设不能用一个参数集合来表示，则该假设检验就是非参数假设检验，一个典型就是正态性检验。

（1）正态性检验：于参数检验比非参数检验更灵敏，因此一旦数据是正态分布的，我们应该使用参数检验，此时对数据进行正态性检验就非常有必要了。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 生成1000个服从正态分布的数据
data_norm = stats.norm.rvs(loc=10, scale=10, size=1000)  # loc: 均值，scale: 标准差，size: 数据个数

# 生成1000个服从卡方分布的数据
# 修正：卡方分布的参数应该是自由度（df），而不是位置参数（loc）和尺度参数（scale）
data_chi = stats.chi2.rvs(df=2, size=1000)  # df: 自由度

# 画出两个概率图
fig = plt.figure(figsize=(12, 6))

# 第一个子图：正态数据的概率图
ax1 = fig.add_subplot(1, 2, 1)
stats.probplot(data_norm, dist="norm", plot=plt)  # 指定分布为正态分布
ax1.set_title("正态分布概率图")
ax1.set_xlabel("理论分位数")
ax1.set_ylabel("样本分位数")

# 第二个子图：卡方分布数据的概率图
ax2 = fig.add_subplot(1, 2, 2)
stats.probplot(data_chi, dist="chi2", sparams=(2,), plot=plt)  # 指定分布为卡方分布，自由度为2
ax2.set_title("卡方分布概率图")
ax2.set_xlabel("理论分位数")
ax2.set_ylabel("样本分位数")

# 显示图形
plt.tight_layout()
plt.show()

概率图可视化确实可以起到初步判断数据正态性的作用。由于数据的复杂性，仅使用一种方法判断正态性有可能产生一定的误差，因此我们通常同时使用多种方法进行判断。如果不同方法得出的结论不同，此时就需要仔细观察数据的特征，寻找结果不一致的原因。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

def check_normality(data: np.ndarray, show_flag: bool = True) -> dict:
    """
    输入参数
    ----------
    data : numpy数组或者pandas.Series
    show_flag : 是否显示概率图
    Returns
    -------
    两种检验的p值；概率图
    """
    # 绘制正态概率图
    if show_flag:
        stats.probplot(data, dist="norm", plot=plt)
        plt.title("正态概率图")
        plt.xlabel("理论分位数")
        plt.ylabel("样本分位数")
        plt.show()

    # 初始化存储p值的字典
    p_values = {}

    # Shapiro-Wilk检验（适用于小样本）
    _, p_values['Shapiro-Wilk'] = stats.shapiro(data)

    # D'Agostino's K-squared检验（适用于大样本）
    _, p_values['Omnibus'] = stats.normaltest(data)

    # 输出结果
    print(f"数据量为{len(data)}的数据集正态性假设检验的结果：----------------")
    for test, p_value in p_values.items():
        print(f"{test}: p-value = {p_value:.4f}")

    return p_values

# 测试数据
data_small = stats.norm.rvs(0, 1, size=30)  # 小样本正态性数据集
data_large = stats.norm.rvs(0, 1, size=6000)  # 大样本正态性数据集

# 调用函数
check_normality(data_small, show_flag=True)
check_normality(data_large, show_flag=True)

数据量为6000的数据集正态性假设检验的结果：----------------
Shapiro-Wilk: p-value = 0.9588
Omnibus: p-value = 0.5587
（2）单组样本均值假定的检验：比较两个样本的总体均值是否相等

例如：某中学高三尖子班举行了一次摸底考试，由于班级人数较多，短时间内很难完成批改与统计，老班想提前知道同学成绩，老班会一些统计学知识，故而操作如下；

抽取已经批改好的部分学生成绩：136,136,134,136,131,133,142,145,137,140 均值137

问：班主任可以认为此次班级平均分与级长定的班级均分137的目标没有显著区别吗？

根据试卷难度，炎德英才划定的清北线恰为137分，问：老班可以认为此次班级平均分与清北线没有差别吗。

最初我也不明白，两者均值都相等了，说明这个班的数学水平已达清北。但进一步学习后我了解到，这是不够的，涉及到统计学中一个重要的概念：样本均值与总体均值的关系。

  这涉及到统计学中一个重要的概念：样本均值与总体均值的关系。仅仅比较样本均值和总体均值是否相等是不够的，因为样本均值只是一个估计值，它可能会受到抽样误差的影响。而统计检验（如单样本t检验）可以帮助我们判断样本均值与总体均值之间的差异是否具有统计学意义。

为什么不能只看均值是否相等？

1. 抽样误差的存在：

   • 即使总体均值是137，由于抽样误差，样本均值可能不完全等于137。例如，你抽取的10个样本的均值是137，但如果再抽取另一组样本，均值可能变成136或138。

2. 样本大小的影响：

   • 样本大小越小，抽样误差越大。例如，样本量为10时，样本均值的波动可能较大；而样本量为1000时，样本均值会更接近总体均值。

举个例子来说明

假设你有以下两组样本数据：

• 样本A：136, 136, 134, 136, 131, 133, 142, 145, 137, 140（均值为137）

• 样本B：136, 136, 134, 136, 131, 133, 142, 145, 137, 150（均值为138）

仅仅比较均值，样本A的均值等于137，样本B的均值不等于137。但样本B的均值138是否真的与总体均值137有显著差异呢？

通过单样本t检验：

• 如果样本B的t检验结果显示p值大于0.05（例如p=0.1），这意味着样本B的均值与总体均值137之间的差异可能是由于抽样误差导致的，而不是真实的差异。

• 如果p值小于0.05（例如p=0.01），则意味着样本B的均值与总体均值137之间存在显著差异。代码如下：

  import numpy as np
  import pandas as pd
  from scipy import stats
  
  def check_mean(data, checkvalue, significance=0.05, alternative='two-sided'):
      """
      输入参数
      ----------
      data : numpy数组或者pandas.Series
      checkvalue : 想要比较的均值
      significance : 显著性水平
      alternative : 检验类型，这取决于我们备择假设的符号：
                    two-sided为双侧检验、greater为右侧检验、less为左侧检验
      输出
      -------
      在两种检验下的p值
      在显著性水平下是否拒绝原假设
      """
      # 初始化存储p值的字典
      pVal = {}
  
      # 正态性数据检验 - t检验
      _, pVal['t-test'] = stats.ttest_1samp(data, popmean=checkvalue, alternative=alternative)
      print('t-test------------------------')
      if pVal['t-test'] < significance:
          print(f"目标值{checkvalue:4.2f}在显著性水平{significance}下不等于样本均值 (p={pVal['t-test']:5.3f}).")
      else:
          print(f"目标值{checkvalue:4.2f}在显著性水平{significance}下无法拒绝等于样本均值的假设 (p={pVal['t-test']:5.3f}).")
  
      # 非正态性数据检验 - Wilcoxon符号秩检验
      try:
          _, pVal['wilcoxon'] = stats.wilcoxon(data - checkvalue, alternative=alternative)
          print('Wilcoxon Signed-Rank Test------------------------')
          if pVal['wilcoxon'] < significance:
              print(f"目标值{checkvalue:4.2f}在显著性水平{significance}下不等于样本均值 (p={pVal['wilcoxon']:5.3f}).")
          else:
              print(f"目标值{checkvalue:4.2f}在显著性水平{significance}下无法拒绝等于样本均值的假设 (p={pVal['wilcoxon']:5.3f}).")
      except ValueError as e:
          print(f"Wilcoxon检验失败：{e}")
  
      return pVal
  
  # 测试数据
  data = np.array([136, 136, 134, 136, 131, 133, 142, 145, 137, 140])
  checkvalue = 137
  
  # 调用函数
  p_values = check_mean(data, checkvalue, significance=0.05, alternative='two-sided')
  print(p_values)

目标值137.00在显著性水平0.05下无法拒绝等于样本均值的假设 (p=1.000).
Wilcoxon Signed-Rank Test------------------------
目标值137.00在显著性水平0.05下无法拒绝等于样本均值的假设 (p=0.812).
{'t-test': np.float64(1.0), 'wilcoxon': np.float64(0.811892226523236)}

结论

班主任可以认为此次班级平均分与级长定的班级均分137的目标没有显著区别。同样，老班可以认为此次班级平均分与清北线没有差别。

小结一下，单样本t检验：1）给出零假设和备择假设

                                         2）用样本均值，总体均值，样本标准差，总体标准差求t统计量

                                         3）确定双尾检验的临界值

                                         4）比较t统计量和临界值，若前者小于后者，则无法拒绝零假设

注明：置信程度：通常用百分比表示（如95%、99%），表示我们有多大把握认为样本数据所反映的结论是正确的。

       自由度：统计分析中自由变化的独立信息的数量

（2）两组样本的均值相等性检验：继续讲这个故事，另一个普通班的老师手上有12份改好的数学试卷，其平均分也是137：

  134,136,135,145,147,140,142,137,139,140,141,135

问：我们可以认为两个班级的均分是相等的吗？

这是一个非常典型的双独立样本的均值检验。这里的独立指的是抽样意义上的独立，而不是统计意义的独立，这里的独立指的是抽样意义上的独立，而不是统计意义的独立

  在本例中，两个班级的授课老师不同，因此两个班学生的英语学习不会受到同一个老师的影响；两个班级考试同时进行，意味着不存在时间差让先考完的同学给后考完的同学通风报信（进而影响受试）。因此，我们可以认为这是两个独立的样本。

  若两个样本的总体都服从正态分布，那么我们可以使用双样本t检验。如果不服从正态分布，则可以使用Mannwhitneyu秩和检验，Mannwhitneyu秩和检验是一种非参数检验。运行下面代码。可以同时输出t值检验和Mannwhitneyu秩和检验的p值：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

# 定义两组数据
group1 = np.array([136, 136, 134, 136, 131, 133, 142, 145, 137, 140])
group2 = np.array([134, 136, 135, 145, 147, 140, 142, 137, 139, 140, 141, 135])

def unpaired_data(group1: np.ndarray, group2: np.ndarray, significance=0.05, alternative='two-sided'):
    """
    对两组独立样本进行均值差异检验，同时输出t检验和Mann-Whitney U检验的p值。
    """
    # 检查输入是否为numpy数组
    if not isinstance(group1, np.ndarray) or not isinstance(group2, np.ndarray):
        raise ValueError("group1 和 group2 必须是 numpy 数组。")

    # 检查数据是否包含NaN或无穷值
    if np.isnan(group1).any() or np.isnan(group2).any():
        raise ValueError("数据中包含 NaN 值，请清理数据。")
    if np.isinf(group1).any() or np.isinf(group2).any():
        raise ValueError("数据中包含无穷值，请清理数据。")

    # 初始化p值存储容器
    pVal = pd.Series(dtype='float64')

    # 1. 方差齐性检验（Levene检验）
    _, pVal['levene'] = stats.levene(group1, group2)

    # 2. t检验
    if pVal['levene'] < significance:
        print(f"在显著性水平 {significance} 下，两组样本的方差不相等(p={pVal['levene']:.4f})，因此使用方差不等的t检验。")
        _, pVal['t-test'] = stats.ttest_ind(group1, group2, equal_var=False, alternative=alternative)
    else:
        print(f"在显著性水平 {significance} 下，不能拒绝两组样本方差相等的假设(p={pVal['levene']:.4f})，因此使用方差相等的t检验。")
        _, pVal['t-test'] = stats.ttest_ind(group1, group2, equal_var=True, alternative=alternative)
    print(f"t检验p值：{pVal['t-test']:.3f}")

    # 3. Mann-Whitney U检验
    try:
        _, pVal['mannwhitneyu'] = stats.mannwhitneyu(group1, group2, alternative=alternative)
        print(f"Mann-Whitney U检验p值：{pVal['mannwhitneyu']:.3f}")
    except Exception as e:
        print(f"Mann-Whitney U检验失败：{e}")

    # 4. 可视化两组样本的散点图
    print('------------------------------------')
    print('两组样本的散点图可视化')
    try:
        plt.plot(group1, 'bx', label='group1')  # group1用蓝色叉号表示
        plt.plot(group2, 'ro', label='group2')  # group2用红色圆圈表示
        plt.legend(loc='best')  # 自动选择最佳位置放置图例
        plt.xlabel('样本索引')
        plt.ylabel('值')
        plt.title('两组样本的散点图')
        plt.show()
    except Exception as e:
        print(f"绘图失败：{e}")

    return pVal

# 调用函数并输出结果
p_values = unpaired_data(group1, group2)
print("p值结果：")
print(p_values)

p值结果：
levene          0.827727
t-test          0.221138
mannwhitneyu    0.259739
dtype: float64

名词解释：

Levene检验是一种用于判断两组数据方差是否相等的统计检验方法。如果p值小于显著性水平，则认为方差不相等；否则认为方差相等。

显著性水平通常用α表示，是一个阈值，用于判断统计检验的结果是否具有统计学意义。常用的显著性水平为0.05或0.01。如果p值小于显著性水平，则拒绝原假设

p值是统计检验的结果，表示在原假设为真的情况下，观察到当前样本或更极端样本的概率。如果p值小于显著性水平，则拒绝原假设。是一种非参数检验方法，不假设数据服从正态分布。它用于比较两组独立样本的分布差异，适合于数据不满足正态分布的情况。

两个检验都表明，两个班级的平均分没有显著差异。

两个样本故意不独立的情况：两个样本分别为同一个体不同收拾时间的结果。

于是陈老师开始了为期一周的魔鬼训练，并在一个星期后又进行了一次全班的测验。陈老师依旧抽取了上次十位同学的成绩，依次为：

139,141,137,136,135,132,141,148,145,139

成对检验也分为两种：若总体服从正态分布，则使用成对t检验；若总体不服从正态分布，则使用成对wilcoxon秩和检验。

import numpy as np
import pandas as pd
from scipy import stats

def paired_data(group1: np.ndarray, group2: np.ndarray, significance=0.05, alternative='two-sided'):
    """
    对两组配对样本进行均值差异检验，同时输出配对 t 检验和 Wilcoxon 符号秩检验的 p 值。

    输入参数
    ----------
    group1/2 : 用于比较的两组数据，注意，两组数据的样本顺序必须相同。
    significance : 显著性水平。
    alternative : 检验类型，取决于备择假设的符号：
        - 'two-sided': 双侧检验，检验两组均值是否不相等。
        - 'greater': 单侧检验，检验 group1 的均值是否小于 group2。
        - 'less': 单侧检验，检验 group1 的均值是否大于 group2。

    输出
    -------
    pVal: pd.Series
        包含 t 检验和 Wilcoxon 符号秩检验的 p 值。
    在显著性水平下是否拒绝原假设。
    """
    pVal = pd.Series(dtype='float64')

    # 1. 配对 t 检验
    # 配对 t 检验用于比较两组配对样本的均值差异，假设数据服从正态分布。
    _, pVal['t-test'] = stats.ttest_rel(group1, group2, alternative=alternative)
    print('t-test------------------------')
    if pVal['t-test'] < significance:
        print(f'在显著性水平 {significance} 下，两组配对样本的均值不相等 (p={pVal["t-test"]:.3f}).')
    else:
        print(f'在显著性水平 {significance} 下无法拒绝两组均值相等的假设 (p={pVal["t-test"]:.3f}).')

    # 2. Wilcoxon 符号秩检验
    # Wilcoxon 符号秩检验是一种非参数方法，用于比较两组配对样本的分布差异，不假设数据服从正态分布。
    # 输入为两组数据的差值。
    _, pVal['wilcoxon'] = stats.wilcoxon(group1 - group2, mode='approx', alternative=alternative)
    print('Wilcoxon 符号秩检验------------------------')
    if pVal['wilcoxon'] < significance:
        print(f'在显著性水平 {significance} 下，两组配对样本的分布存在显著差异 (p={pVal["wilcoxon"]:.3f}).')
    else:
        print(f'在显著性水平 {significance} 下无法拒绝两组分布相同的假设 (p={pVal["wilcoxon"]:.3f}).')

    return pVal

# 示例数据
pre = np.array([136, 136, 134, 136, 131, 133, 142, 145, 137, 140])  # 第一次测验
post = np.array([139, 141, 137, 136, 135, 132, 141, 148, 145, 139])  # 第二次测验

# 调用函数
p_values = paired_data(pre, post, 0.05)
print("p值结果：")
print(p_values)

t-test------------------------
在显著性水平 0.05 下，两组配对样本的均值不相等 (p=0.039).
Wilcoxon 符号秩检验------------------------
在显著性水平 0.05 下，两组配对样本的分布存在显著差异 (p=0.049).
p值结果：
t-test      0.039370
wilcoxon    0.048997
dtype: float64
故而老师的训练起效果了。

（3）方差分析-多组样本间的均值相等性检验

要检验不同总体间的均值差异程度，对比各样本间的差异程度是非常自然的想法。同时还要注意样本内部数值的差异程度，方差越大，代表抽取的样本更加难以代表总体的样本。

引入方差分析，最简单的方法是样本间的差异程度除以样本内数据的差异程度。尽管在大样本下，非正态性数据的方差分析也是稳健的，但是在小样本下，对非正态性数据做方差分析还是可能存在误差。

对于小样本数据的kruskalwallis检验：

_, pVal['anova_oneway_notnormal'] = stats.mstats.kruskalwallis(group1, group2, group3)
print('若样本不服从正态分布，单因素方差分析的p值为{}'.format(pVal['anova_oneway_notnormal']))
if pVal['anova_oneway_notnormal'] < 0.05:
    print('检验在0.05的显著性水平下显著，多组样本中至少存在一组样本均值与其它样本的均值不相等。')

警告: 方差齐性检验的p值小于0.05: p=0.045847，方差分析结果在小样本下可能不准确
-------------------------------
若样本服从正态分布，单因素方差分析的p值为0.043589
检验在0.05的显著性水平下显著，多组样本中至少存在一组样本均值与其它样本的均值不相等。
---------------------------------
若样本不服从正态分布，单因素方差分析的p值为0.123363

2.2.3 随机过程和随机模拟

随机过程：实质是一个无穷函数组

假设气象学家要研究未来每一天的气温变化，每一天的平均气温用一个随机变量表示，于是得到无穷多个随机变量，将无穷多个变量放在一起组成一个集合，就称随机过程。

无穷多个随机变量首先会有先后次序之分，不同的随机变量之间彼此可能会产生影响，而非独立分散的。

学习目标：掌握如何使用简单的simpy进行仿真的流程：

案例1：为了改善道路的路面情况（道路经常维修，坑坑洼洼），因此想统计一天中有多少车辆经过，因为每天的车辆数都是随机的，一般来说有两种技术解决这个问题：

（1） 在道路附近安装一个计数器或安排一个技术人员，在一段长时间的天数（如365天）每天24h统计通过道路的车辆数。

（2） 使用仿真技术大致模拟下道路口的场景，得出一个近似可用的仿真统计指标。

由于方案（1）需要花费大量的人力物力以及需要花费大量的调研时间，虽然能得出准确的结果，但是有时候在工程应用中并不允许。因此，我们选择方案（2），我们通过一周的简单调查，得到每天的每个小时平均车辆数：[30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40]，通过利用平均车辆数进行仿真。

import simpy
import numpy as np

# 定义路口类
class Road_Crossing:
    def __init__(self, env):
        self.road_crossing_container = simpy.Container(env, capacity=1e8, init=0)

# 定义车辆到达过程
def come_across(env, road_crossing, lmd):
    while True:
        body_time = np.random.exponential(1.0 / (lmd / 60))  # 指数分布时间，单位为分钟
        yield env.timeout(body_time)  # 等待 body_time 分钟
        yield road_crossing.road_crossing_container.put(1)  # 向容器中添加一辆车

# 每小时平均车辆数（根据调查数据）
lmd_ls = [30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40]

# 模拟参数
hours = 24  # 一天24小时
days = 3    # 模拟3天
car_sum = []  # 存储每一天的通过路口的车辆数之和

print('仿真开始：')
for day in range(days):
    day_car_sum = 0  # 记录每天的通过车辆数之和
    for hour, lmd in enumerate(lmd_ls):
        env = simpy.Environment()  # 创建仿真环境
        road_crossing = Road_Crossing(env)  # 创建路口对象
        come_across_process = env.process(come_across(env, road_crossing, lmd))  # 启动车辆到达过程
        env.run(until=60)  # 模拟60分钟

        # 累加当前小时的车辆数
        day_car_sum += road_crossing.road_crossing_container.level

        # 每隔4小时打印一次车辆数
        if hour % 4 == 0:
            print(f"第{day + 1}天，第{hour + 1}小时的车辆数：{road_crossing.road_crossing_container.level}")

    # 将当天的车辆总数加入列表
    car_sum.append(day_car_sum)

# 输出每天通过路口的车辆总数
print("每天通过交通路口的车辆数之和为：", car_sum)

仿真开始：
第1天，第1小时的车辆数：29
第1天，第5小时的车辆数：7
第1天，第9小时的车辆数：243
第1天，第13小时的车辆数：88
第1天，第17小时的车辆数：202
第1天，第21小时的车辆数：154
第2天，第1小时的车辆数：21
第2天，第5小时的车辆数：5
第2天，第9小时的车辆数：223
第2天，第13小时的车辆数：92
第2天，第17小时的车辆数：221
第2天，第21小时的车辆数：164
第3天，第1小时的车辆数：37
第3天，第5小时的车辆数：7
第3天，第9小时的车辆数：245
第3天，第13小时的车辆数：94
第3天，第17小时的车辆数：197
第3天，第21小时的车辆数：170
每天通过交通路口的车辆数之和为： [2452, 2457, 2510]

 案例2：现在，我们来仿真“每天的商店营业额”这个复合泊松过程吧。首先，我们假设每个小时进入商店的平均人数为：[10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10]，每位顾客的平均花费为：10元（大约一份早餐吧），请问每天商店的营业额是多少？

import simpy
import numpy as np

# 定义商店类
class Store_Money:
    def __init__(self, env):
        self.store_money_container = simpy.Container(env, capacity=1e8, init=0)

# 定义顾客购买过程
def buy(env, store_money, lmd, avg_money):
    while True:
        # 指数分布时间间隔，模拟顾客到达（单位：分钟）
        body_time = np.random.exponential(1.0 / (lmd / 60))
        yield env.timeout(body_time)  # 等待 body_time 分钟

        # 每个顾客的消费金额，假设服从泊松分布
        money = np.random.poisson(lam=avg_money)
        yield store_money.store_money_container.put(money)  # 将消费金额加入容器

# 模拟参数
hours = 24  # 一天24小时
days = 3    # 模拟3天
avg_money = 10  # 每个顾客平均消费金额
lmd_ls = [10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10]  # 每小时平均进入商店的人数
money_sum = []  # 存储每一天的商店营业额总和

print('仿真开始：')
for day in range(days):
    day_money_sum = 0  # 记录每天的营业额之和
    for hour, lmd in enumerate(lmd_ls):
        env = simpy.Environment()  # 创建仿真环境
        store_money = Store_Money(env)  # 创建商店对象
        store_money_process = env.process(buy(env, store_money, lmd, avg_money))  # 启动顾客购买过程
        env.run(until=60)  # 模拟60分钟

        # 累加当前小时的营业额
        day_money_sum += store_money.store_money_container.level

        # 每隔4小时打印一次营业额
        if hour % 4 == 0:
            print(f"第{day + 1}天，第{hour + 1}小时的营业额：{store_money.store_money_container.level}")

    # 将当天的营业额总数加入列表
    money_sum.append(day_money_sum)

# 输出每天商店的营业额总和
print("每天商店的营业额总和为：", money_sum)

  

c

仿真开始：
第1天，第1小时的营业额：92
第1天，第5小时的营业额：79
第1天，第9小时的营业额：1022
第1天，第13小时的营业额：1002
第1天，第17小时的营业额：535
第1天，第21小时的营业额：623
第2天，第1小时的营业额：99
第2天，第5小时的营业额：106
第2天，第9小时的营业额：1033
第2天，第13小时的营业额：842
第2天，第17小时的营业额：553
第2天，第21小时的营业额：607
第3天，第1小时的营业额：80
第3天，第5小时的营业额：79
第3天，第9小时的营业额：1001
第3天，第13小时的营业额：1109
第3天，第17小时的营业额：520
第3天，第21小时的营业额：619
每天商店的营业额总和为： [11382, 11450, 11616]

进程已结束，退出代码为 0

案例3：艾滋病发展过程分为四个阶段（状态），急性感染期（状态 1）、无症状期（状态 2）， 艾滋病前期（状态 3）, 典型艾滋病期（状态 4）。艾滋病发展过程基本上是一个不可逆的过程,即：状态1 -> 状态2 -> 状态3 -> 状态4。现在收集某地600例艾滋病防控数据，得到以下表格：

import numpy as np

def get_years_dist(p0, P, N):
    """
    计算N期转移后的状态分布。

    参数:
    p0: 初始状态分布向量 (numpy数组)
    P: 转移概率矩阵 (numpy数组)
    N: 转移期数 (整数)

    返回:
    N期转移后的状态分布 (numpy数组)
    """
    P1 = P.copy()  # 避免修改原始矩阵
    for i in range(N):
        P1 = np.matmul(P1, P)  # 矩阵相乘，计算N期转移矩阵
    return np.matmul(p0, P1)  # 初始状态向量与N期转移矩阵相乘

# 初始状态分布
p0 = np.array([0, 1, 0, 0])  # 初始状态为第二个状态（索引为1）

# 转移概率矩阵
P = np.array([
    [10.0/80, 62.0/80, 5.0/80, 3.0/80],
    [0, 140.0/290, 93.0/290, 57.0/290],
    [0, 0, 180.0/220, 40.0/220],
    [0, 0, 0, 1]
])

# 转移期数
N = 10

# 计算N期转移后的状态分布
result = get_years_dist(p0, P, N)
print(f"{N}期转移后，状态分布为：", np.round(result, 4))

10期转移后，状态分布为： [0.000e+00 3.000e-04 1.048e-01 8.948e-01]

2.3 数据可视化

数据可视化在注重图像观感的同时要注重表达结论;

2.3.1 Python三大数据可视化工具库的简介

Matplotlib是一个面向对象的绘图工具库，pyplot是Matplotlib最常用的一个绘图接口，调用方法如下：

import matplotlib.pyplot as plt

所谓的面向对象，是在说图形窗口，绘图区域，图形元素都是由代码创建和操作的。“Matplotlib的每一句代码都是往纸上添加一个绘图特征”。优点是非常简单易懂，而且能绘制复杂图表；缺点也是十分明显的，如果绘制复杂图表的时候一步一步地绘制，代码量还是十分巨大的。Seaborn是在Matplotlib的基础上的再次封装，是对Matplotlib绘制统计图表的简化。下面，我们一起看看Seaborn的基本绘图逻辑。

Seaborn主要用于统计分析绘图的，它是基于Matplotlib进行了更高级的API封装。Seaborn比matplotlib更加易用，尤其在统计图表的绘制上，因为它避免了matplotlib中多种参数的设置。Seaborn与matplotlib关系，可以把Seaborn视为matplotlib的补充。 

一起使用Matplotlib和Seaborn，两者的结合应该属于Python的数据可视化的一大流派吧。

ggplot2 和 Plotnine

from plotnine import *
from plotnine.data import mpg  # 引入 Plotnine 自带的 mpg 数据集

# 查看数据集的前几行
print(mpg.head())

# 绘制汽车在不同驱动系统下，发动机排量与耗油量的关系
p1 = (
    ggplot(mpg, aes(x='displ', y='hwy', color='drv'))  # 设置数据映射图层
    + geom_point()  # 绘制散点图图层
    + geom_smooth(method='lm', se=False)  # 绘制线性回归线图层
    + labs(x='Displacement', y='Highway Mileage', title='Engine Displacement vs. Highway Mileage')  # 设置标签和标题
    + theme_minimal()  # 使用简洁的主题
)

print(p1)  # 展示图像

Plotnine无法绘制类似于饼图、环图等图表。为了解决这个问题，在绘制直角坐标系的图表时，我们可以使用Plotnine进行绘制，当涉及极坐标图表时，我们使用Matplotlib和Seaborn进行绘制。

2.3.2 基本图标Quick Start

类别型图表常常有：柱状图、横向柱状图（条形图）、堆叠柱状图、极坐标的柱状图、词云、雷达图、桑基图等等。

## Matplotlib绘制单系列柱状图：不同城市的房价对比

 

# Plotnine绘制单系列柱状图：不同城市的房价对比

此外还有各种各样的图表，在这里我大体说一下怎么绘制，

（2）关系型图表：关系型图表一般表现为：X数值与Y数值之间的关系，如：是否是线性关系、是否有正向相关关系等等。一般来说，关系可以分为：数值型关系、层次型关系和网络型关系。

（2）关系型图表：关系型图表一般表现为：X数值与Y数值之间的关系，如：是否是线性关系、是否有正向相关关系等等。一般来说，关系可以分为：数值型关系、层次型关系和网络型关系。

# 使用Matplotlib和四个图说明相关关系：
x = np.random.randn(100)*10
y1 = np.random.randn(100)*10
y2 = 2 * x + 1 + np.random.randn(100)
y3 = -2 * x + 1 + np.random.randn(100)
y4 = x**2 + 1 + np.random.randn(100)

plt.figure(figsize=(12, 12))

plt.subplot(2,2,1)  #创建两行两列的子图，并绘制第一个子图
plt.scatter(x, y1, c='dodgerblue', marker=".", s=50)
plt.xlabel("x")
plt.ylabel("y1")
plt.title("y1与x不存在关联关系")

plt.subplot(2,2,2)  #创建两行两列的子图，并绘制第二个子图
plt.scatter(x, y2, c='tomato', marker="o", s=10)
plt.xlabel("x")
plt.ylabel("y2")
plt.title("y2与x存在关联关系")

plt.subplot(2,2,3)  #创建两行两列的子图，并绘制第三个子图
plt.scatter(x, y3, c='magenta', marker="o", s=10)
plt.xlabel("x")
plt.ylabel("y3")
plt.title("y3与x存在关联关系")

plt.subplot(2,2,4)  #创建两行两列的子图，并绘制第四个子图
plt.scatter(x, y4, c='deeppink', marker="s", s=10)
plt.xlabel("x")
plt.ylabel("y3")
plt.title("y4与x存在关联关系")

plt.show()

上面四个图像分别给出了散点，线性，平方的关系，使用mat绘制了简单的图像，将4组数据合并到一个DataFrame中，并添加类别标签。

import numpy as np
import pandas as pd
from plotnine import *

# 生成数据
x = np.random.randn(100) * 10
y1 = np.random.randn(100) * 10
y2 = 10 * x + 1 + np.random.randn(100)
y3 = -10 * x + 1 + np.random.randn(100)
y4 = x**2 + 1 + np.random.randn(100)

# 创建 DataFrame
df = pd.DataFrame({
    'x': np.concatenate([x, x, x, x]),
    'y': np.concatenate([y1, y2, y3, y4]),
    'class': ['y1'] * 100 + ['y2'] * 100 + ['y3'] * 100 + ['y4'] * 100
})

# 绘制图表
p1 = (
    ggplot(df) +
    geom_point(aes(x='x', y='y', fill='class', shape='class'), color='black', size=2) +
    scale_fill_manual(values=('#00AFBB', '#FC4E07', '#00589F', '#F68F00')) +
    theme(text=element_text(family="Songti SC")) +
    labs(title="不同关系的散点图", x="X 轴", y="Y 轴") +
    facet_wrap('~class', ncol=2)  # 按类别分面绘制
)

print(p1)

 

还有

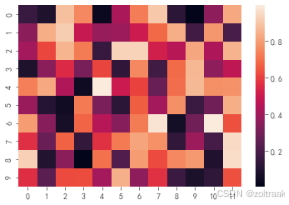这是相关系数矩阵图

3）分布型图表：所谓数据的分布，其实就是数据在哪里比较密集，那里比较稀疏，描述数据的密集或者稀疏情况实际上可以用频率或者概率。

注意，如果某个数据集不是Python中自带的数据集，需要下载。

个人看法是，这些python的数据可视化都相当粗糙，还是要靠论文手做图像。

2.4 插值模型

2.4.1三次样条插值

作用是填充缺失的数据，以我什么都没有学的脑袋只能相想到取平均值，还有没有更巧妙的方法呢：让我们回想一下高中数学中药画函数草图的过程，得到了一系列的点，要平滑地将其用曲线连接，于是，想到用一个三次函数来拟合点与点，从而是我们的图像在函数点，一介导数和二阶导数是光滑的，2.4.2 拉格朗日插值

数学基础:

拉格朗日插值简单了解

def lagrange(x0,y0,x):
    y=[]
    for k in range(len(x)):
        s=0
        for i in range(len(y0)):
           t=y0[i]
           for j in range(len(y0)):
              if i!=j:
                t*=(x[k]-x0[j])/(x0[i]-x0[j])
           s+=t
        y.append(s)
    return y

---

from scipy.interpolate import interp1d
x0=[1,2,3,4,5]
y0=[1.6,1.8,3.2,5.9,6.8]
x=np.arange(1,5,1/30)
f1=interp1d(x0,y0,'linear')
y1=f1(x)
f2=interp1d(x0,y0,'cubic')
y2=f2(x)
y3=lagrange(x0,y0,x)
plt.plot(x0,y0,'r*')
plt.plot(x,y1,'b-',x,y2,'y-',x,y3,'r-')
plt.show()

 

笔者作为小白，希望得到您的指正