L1/L2正则化与集成学习

原创已于 2025-11-04 15:40:16 修改 · 716 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能 #算法

于 2025-11-03 22:51:23 首次发布

机器学习专栏收录该内容

2 篇文章

订阅专栏

一、正则化与先验、后验概率

先验概率（Prior）：模型训练前对事物的初始假设，无任何数据支撑时的默认判断。例如抛硬币前，默认正反面概率均为50%，这是对“硬币公平性”的先验认知。

后验概率（Posterior）：基于实际观测数据调整后的概率，数据量越大，后验结果越精准。例如连续抛10次硬币，仅1次反面，会修正先验认知，怀疑硬币不公平。

正则化的本质：正则化（L1、L2）对应机器学习中的先验信息，训练数据对应后验信息。模型训练需结合先验（正则项）和后验（训练数据），超参数λ控制对先验的依赖程度。（详细可见https://www.zhihu.com/question/23536142/answer/72762412337第二条评论）

下面我们来举个例子：

对于损失函数 $J_{L2}(\theta) = \frac{1}{m} \sum_{i=1}^{m} L(h_\theta(x^{(i)}), y^{(i)}) + \lambda \sum_{j=1}^{n} \theta_j^2$

其中，m是样本数量， $\frac{1}{m} \sum_{i=1}^{m} L(h_\theta(x^{(i)}), y^{(i)})$ 是单个样本的损失， $\lambda$ 是正则化超参数，n是特征数量， $\theta_j$ 是第 j 个特征的权重参数。

假设参数 $\theta$ 服从正态分布，当 $\theta$ 过大时，会导致损失函数 $J_{L2}(\theta)$ 增大，因此正则项 $\lambda \sum_{j=1}^{n} \theta_j^2$ 会将参数权重压缩尽可能至较小值（但不为 0），而为了让 $\frac{1}{m} \sum_{i=1}^{m} L(h_\theta(x^{(i)}), y^{(i)})$ 项的值尽可能小，模型在学习过程中会倾向于让对学习无关的权重趋向于0，从而防止模型过拟合。

超参数λ的影响因素 - 先验方差：先验方差越大，λ应越小，降低先验对模型的约束；先验方差越小，λ应越大，强化先验的指导作用。当样本数量多、质量高时，可降低对先验的依赖，λ设较小值；样本质量低、存在污染时，需增大λ，增强先验约束以避免模型受劣质数据影响。

二、模型集成

1. 核心思想：通过构建多个子模型，融合其预测结果，降低模型对特定特征或极端值的依赖，提升预测的稳定性和泛化能力。类比长跑运动员在不同海拔训练，避免单一环境导致的能力局限。

2. 特征集成策略 - 子模型构建：每个子模型仅使用部分特征（人工或自动舍弃部分特征），例如有3个特征x1、x2、x3，子模型1舍弃x2，子模型2舍弃x3，子模型3舍弃x1。

结果融合：汇总所有子模型的预测得分，相比单一模型，集成模型结果更平稳，避免因个别特征污染导致预测大幅波动。

3. 集成结果融合技巧 - 不推荐直接对预测概率求平均（方案一），推荐对模型输出的原始得分求和后再映射到概率区间（方案二）。

示例：

对于 $z = w_1x_1 + w_2x_2 + \dots + w_nx_n + w_0$

我们令 $w_1=0$ 作为模型 $z_1\left ( X \right )$ ，令 $w_2=0$ 作为模型 $z_2\left ( X\right )$ ， $\cdots$ ，令 $w_n=0$ 作为模型 $z_n\left ( X \right )$ ，该操作实际上和正则化一样，也是加入了先验知识，在模型集成中，我们的先验是某个特征的概率恒等于0，即该项的权重分布是确定已知的。

接下来我们通过Sigmoid函数映射得到概率 $y = \frac{1}{1 + e^{-z}}$ ，

方案一：直接对预测概率做平均

$y = \frac{y_1 + y_2 + \dots + y_n}{n} \quad$

eg.若两个模型预测概率均为0.8（ $z_1=z_2\approx 1.386$ ），平均后仍为0.8。

方案二：两个模型原始得分求和后映射概率，该方法通常情况下比方案一要更好。

先对模型输出求和 $z = z_1 + z_2 + \dots + z_n$

再转为概率 $y = \frac{1}{1 + e^{-z}} \quad (y \in (0,1))$

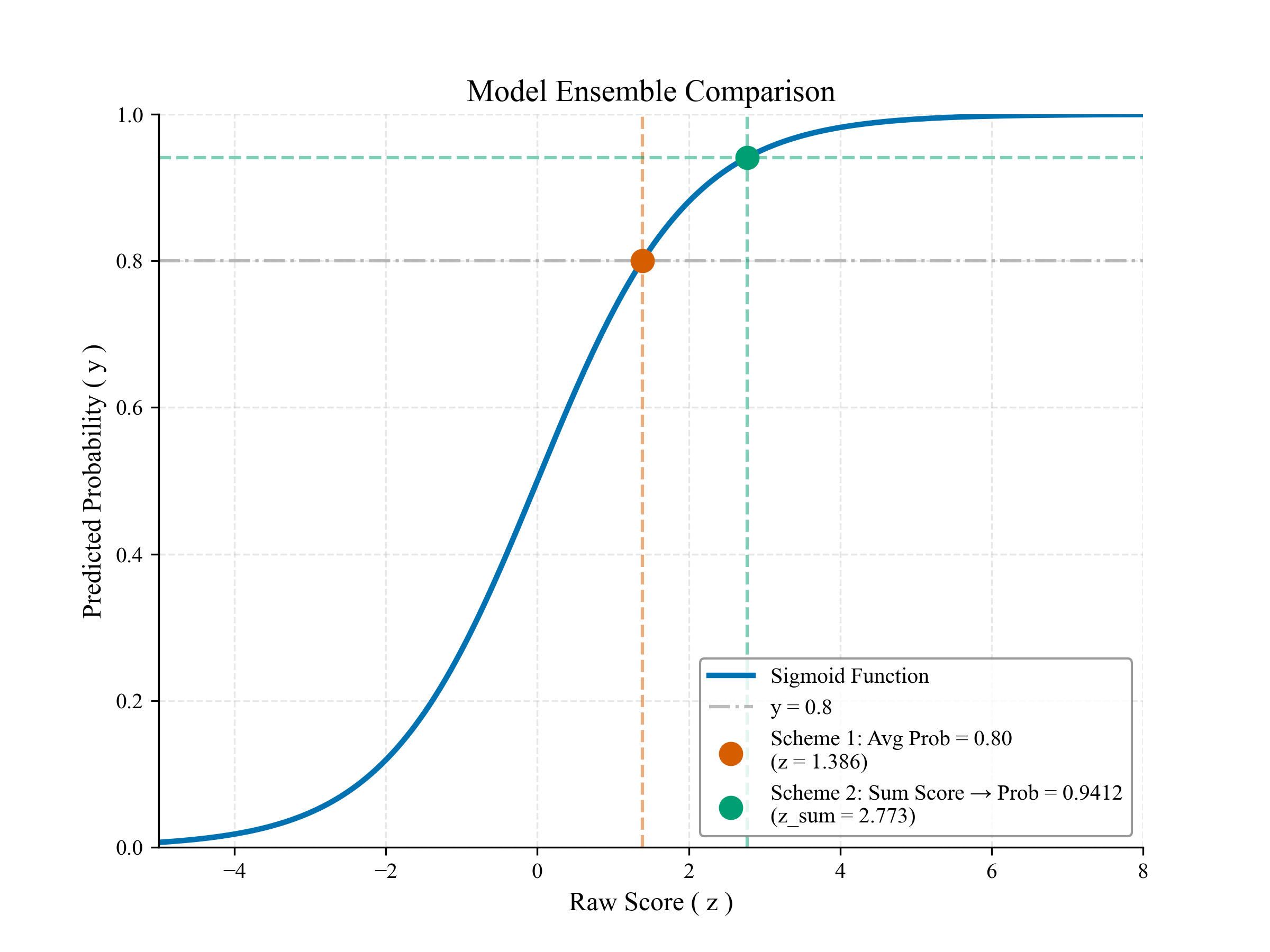
如图所示， $z_{sum} = z_1+z_2\approx 2.773$ ，结果为0.9412，会高于0.8，如何理解这个结果呢，模型 $z_1\left ( X \right )$ 和 $z_2\left ( X\right )$ 都是在去除某个特征后单独预测都能得到0.8，那么当模型同时对这两个特征进行学习时，可能能够得到更高的置信度，因此模型的最终预测概率更高。

若某模型预测概率为0.5（随机猜测，对应原始得分z=0）， $z_{sum} = z_1+z_2$ 求和后不影响最终结果，自动过滤无效模型，而采用方案一得到的结果为 $y=\frac{0.8+0.5}{2}=0.65$ ，将无效模型也算入其中，因此方案二往往比方案一更优。

三、L1/L2正则化VS集成学习

L1/L2正则化和集成学习本质上都是加入先验来防止模型过拟合，其优缺点如下：

方法	模型集成	L1/L2 正则化
核心逻辑	多个子模型各用部分特征，全量依赖部分特征	单个模型用全量特征，对每个特征部分依赖
优缺点	预测稳定、泛化能力强；训练成本高、耗时久	训练高效；稳定性弱于集成，易受极端值影响

方法

模型集成

L1/L2 正则化

核心

逻辑

多个子模型各用部分特征，全量依赖部分特征

单个模型用全量特征，对每个特征部分依赖

优缺点

预测稳定、泛化能力强；

训练成本高、耗时久

训练高效；

稳定性弱于集成，易受极端值影响