反步法设计步骤及仿真验证（非线性系统）

考虑以下单输入，单输出非线性系统：

反步法的设计思想是每一个子系统   中  为虚拟控制，通过适当的虚拟反馈,使得系统的前面状态达到渐进稳定。但是系统的解一般不满足，因此我们引入误差变量，期望通过控制作用，使得  与虚拟反馈  间具有某种渐进特性，从而实现整个系统的渐进稳定。

定义以下误差坐标变换（反步法的坐标变换）

 代表虚拟控制器

反步法设计步骤如下(不断构造李雅普诺夫函数使系统稳定)：

Step1:

定义李雅普诺夫函数为：

显而易见    >0,  对  求导得：

将    带入 得：

根据  坐标变换    可知，

为了使系统稳定，让  

即：

显然，如果  = 0,（即：），由可知，渐进稳定。但是一般情况,此时我们再引入虚拟控制  使得误差 具有期望的渐进性态。为此，我们进行下一步设计

Step2:

定义李雅普诺夫函数为：

显而易见    >0,  对 求导得：

将   带入上式可得：

将带入上式可得：

为了使得<0,设计控制器如下：

其中m为正参数 将  带入 得:

仿真验证：

设置初始值为：参数设置为：

 和 趋于稳定如图所示：

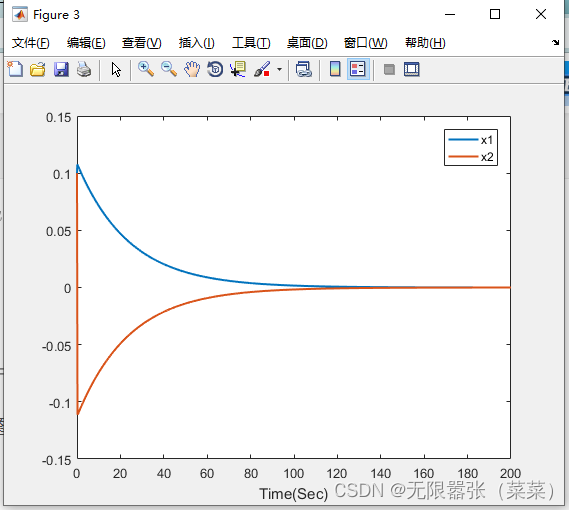
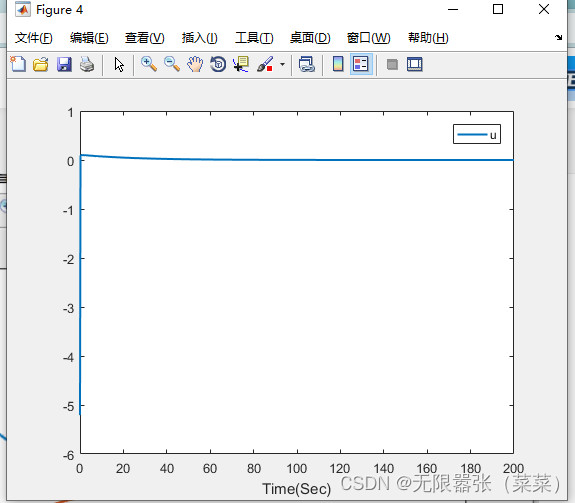
控制器如图所示：