5.4 先验
贝叶斯统计最受争议的就是对先验的依赖.贝叶斯主义者认为这是不可避免的,因为没有人是白板一片(tabula rasa/blank slate):所有的推测都必须是以客观世界的某些假设为条件的.不过人们还是希望能够尽量缩小事先假设的影响.接下来就简要讲一下实现这个目的的几种方法.
5.4.1 无信息先验
如果关于 θ \theta θ应该是啥样没有比较强的事先认识,通常都会使用无信息先验(uninformative or non-informative prior),然后就去"让数据自己说话".
不过设计一个无信息先验还是需要点技巧的.例如,伯努利参数 θ ∈ [ 0 , 1 ] \theta\in [0,1] θ∈[0,1].有人可能会觉得最无信息的先验应该是均匀分布 B e t a ( 1 , 1 ) Beta(1,1) Beta(1,1).不过这时候后验均值就是 E [ θ ∣ D ] = N 1 + 1 N 1 + N 0 + 2 E[\theta|D]=\frac{N_1+1}{N_1+N_0+2} E[θ∣D]=N1+N0+2N1+1,其中的最大似然估计(MLE)为 N 1 N 1 + N 0 \frac{N_1}{N_1+N_0} N1+N0N1.因此就可以发现这个先验也并不是完全无信息的.
很显然,通过降低伪计数(pseudo counts)的程度(magnitu),就可以降低先验的影响.综上所述,最无信息的先验应该是:
lim c → 0 B e t a ( c , c ) = B e t a ( 0 , 0 ) \lim_{c\rightarrow 0}Beta(c,c)=Beta(0,0) limc→0Beta(c,c)=Beta(0,0)(5.49)
上面这个是在0和1两个位置有质量的等价点的混合(a mixture of two equal point masses at 0 and 1),参考(Zhu and Lu 2004).这也叫做Haldane先验(Haldane prior).要注意这个Haldane先验是一个不适当先验,也就是积分不为1.不过只要能看到至少有一次人头朝上以及至少有一次背面朝上,这个后验就是适当的.
在本书5.4.2.1,会论证"正确"的无信息先验是 B e t a ( 1 2 , 1 2 ) Beta(\frac12,\frac12) Beta(21,21).很明显这三个先验在实际使用的时候差异很可能是可以忽略不计的.通常来说,都可以进行敏感度分析,也就是检测建模假设的变化对模型结论和预测变化的影响,这种敏感度分析包含了对先验的选择,也包含了似然率的选择以及对数据的处理过程.如果结论是对于模型假设来说并不敏感,那么就可以对结果更有信心了.
5.4.2 杰弗里斯先验论(Jeffreys priors)*
哈罗德 杰弗里斯(Harold Jeffreys)设计了一个通用技巧来创建无信息先验.得到的就是杰弗里斯先验论(Jeffreys prior).关键之处是观察到如果 p ( ϕ ) p(\phi) p(ϕ)是无信息的,那么对这个先验重新参数化,比如使用某函数h得到的 θ = h ( ϕ ) \theta=h(\phi) θ=h(ϕ),应该也是无信息的.然后就可以更改方程变量:
p θ ( θ ) = p ϕ ( ϕ ) ∣ d ϕ d θ ∣ p_\theta(\theta)= p_\phi(\phi)|\frac{d\phi}{d\theta}| pθ(θ)=pϕ(ϕ)∣dθdϕ∣(5.50)
所以先验会总体上有变化.然后选择
p ϕ ( ϕ ) ∝ ( I ( ϕ ) ) 1 2 p_\phi(\phi)\propto (I(\phi))^{\frac12} pϕ(ϕ)∝(I(ϕ))21(5.51)
其中的 I ( ϕ ) I(\phi) I(ϕ)是费舍信息矩阵(Fisher information matrix):
I ( ϕ ) = △ − E [ ( d log p ( X ∣ ϕ ) d ϕ ) 2 ] I(\phi) \overset\triangle{=} -E[(\frac{d\log p(X|\phi)}{d\phi} )^2] I(ϕ)=△−E[(dϕdlogp(X∣ϕ))2](5.52)
这是对预期的负对数似然函数的度量,也是对最大似然估计的稳定性的度量,参考本书6.2.2.于是就有:
d log p ( x ∣ θ ) d θ = d log p ( x ∣ ϕ ) d ϕ d ϕ d θ \frac{d\log p(x|\theta)}{d\theta}=\frac{d\log p(x|\phi)}{d\phi}\frac{d\phi}{d\theta} dθdlogp(x∣θ)=dϕdlogp(x∣ϕ)dθdϕ(5.53)
开平方,然后去对x的期望,就得到了:
I ( θ ) = − E [ ( d log p ( X ∣ θ ) d θ ) 2 ] = I ( ϕ ) ( d ϕ d θ ) 2 (5.54) I ( θ ) 1 2 = I ( ϕ ) 1 2 ∣ d ϕ d θ ∣ (5.55) \begin{aligned} I(\theta)&= -E[(\frac{d\log p(X|\theta)}{d\theta} )^2]=I(\phi)(\frac{d\phi}{d\theta})^2 &\text{(5.54)}\\ I(\theta)^{\frac{1}{2}} &= I(\phi)^{\frac12}|\frac{d\phi}{d\theta}| &\text{(5.55)}\\ \end{aligned} I(θ)I(θ)21=−E[(dθdlogp(X∣θ))2]=I(ϕ)(dθdϕ)2=I(ϕ)21∣dθdϕ∣(5.54)(5.55)
所以能发现变换后的先验是:
p θ ( θ ) = p ϕ ( ϕ ) ∣ d ϕ d θ ∣ ∝ ( I ( ϕ ) ) 1 2 ∣ d ϕ d θ ∣ = I ( θ ) 1 2 p_\theta(\theta)=p_\phi(\phi)|\frac{d\phi}{d\theta}|\propto (I(\phi))^{\frac12}|\frac{d\phi}{d\theta}| =I(\theta)^{\frac12} pθ(θ)=pϕ(ϕ)∣dθdϕ∣∝(I(ϕ))21∣dθdϕ∣=I(θ)21(5.56)
所以就说明
p
θ
(
θ
)
p_\theta(\theta)
pθ(θ)和
p
ϕ
(
ϕ
)
p_\phi(\phi)
pϕ(ϕ)是一样的.
接下来举几个例子.
5.4.2.1 样例:伯努利模型和多重伯努利模型的杰弗里斯先验论(Jeffreys priors)
设X服从伯努利分布,即 X ∼ B e r ( θ ) X\sim Ber(\theta) X∼Ber(θ).一个单独样本(single sample)的对数似然函数为:
log p ( X ∣ θ ) = X ∣ l o g θ ( 1 − X ) log ( 1 − θ ) \log p(X|\theta) =X|log \theta(1-X)\log(1-\theta) logp(X∣θ)=X∣logθ(1−X)log(1−θ)(5.57)
得分函数(score function)正好就是对数似然函数的梯度:
s ( θ ) = △ d d θ log p ( X ∣ θ ) = X θ − 1 − X ( 1 − θ ) 2 s(\theta)\overset\triangle{=}\frac{d}{d\theta}\log p(X|\theta)=\frac{X}{\theta}-\frac{1-X}{(1-\theta)^2} s(θ)=△dθdlogp(X∣θ)=θX−(1−θ)21−X(5.58)
观测信息(observed information)就是对数似然函数的二阶导数(second derivative):
J ( θ ) = − d 2 d θ 2 log p ( X ∣ θ ) = − s ′ ( θ ∣ X ) = X θ 2 + 1 − X ( 1 − θ ) 2 J(\theta)=-\frac{d^2}{d\theta^2}\log p(X|\theta)=-s'(\theta|X)=\frac{X}{\theta^2}+\frac{1-X}{(1-\theta)^2} J(θ)=−dθ2d2logp(X∣θ)=−s′(θ∣X)=θ2X+(1−θ)21−X(5.59)
费舍信息矩阵(Fisher information)正好就是期望信息矩阵(expected information):
I ( θ ) = E [ J ( θ ∣ X ) ∣ X ∼ θ ] = θ θ 2 + 1 − θ ( 1 − θ ) 2 = 1 θ ( 1 − θ ) I(\theta)=E[J(\theta|X)|X\sim \theta]=\frac{\theta}{\theta^2}+\frac{1-\theta}{(1-\theta)^2}=\frac{1}{\theta(1-\theta)} I(θ)=E[J(θ∣X)∣X∼θ]=θ2θ+(1−θ)21−θ=θ(1−θ)1(5.60)
因此杰弗里斯先验(Jeffreys’ prior)为:
$p(\theta)\propto \theta{-\frac12}(1-\theta){-\frac12}=\frac{1}{\sqrt{\theta(1-\theta)}}\propto Beta(\frac12,\frac12) $(5.61)
然后考虑有K个状态的多重伯努利随机变量.很明显对应的杰弗里斯先验(Jeffreys’ prior)为:
p ( θ ) ∝ D i r ( 1 2 , . . . , 1 2 ) p(\theta)\propto Dir(\frac12,...,\frac12) p(θ)∝Dir(21,...,21)(5.62)
要注意这个和更明显的选择 $Dir(\frac1K,…,\frac1K),Dir(1,…,1) $是不一样的.
5.4.2.2 样例:局部和缩放参数的杰弗里斯先验论(Jeffreys priors)
可以对一个局部参数(location parameter)取杰弗里斯先验(Jeffreys prior),比如以正态分布均值为例,就是 p ( μ ) ∝ 1 p(\mu)\propto 1 p(μ)∝1.这是一个转换不变先验(translation invariant prior),满足下述性质,即分配到任意区间[A,B]的概率质量等于分配另一个等宽区间[A-c,B-c]的概率质量.也就是:
∫ A − c B − c p ( μ ) d μ = ( A − c ) − ( B − c ) = ( A − B ) = ∫ A B p ( μ ) d μ \int^{B-c}_{A-c}p(\mu)d\mu=(A-c)-(B-c)=(A-B)=\int^B_Ap(\mu)d\mu ∫A−cB−cp(μ)dμ=(A−c)−(B−c)=(A−B)=∫ABp(μ)dμ(5.63)
这可以通过使用 p ( μ ) ∝ 1 p(\mu)\propto 1 p(μ)∝1来实现,可以使用一个有限变量的正态分布来近似,即 p ( μ ) = N ( μ ∣ 0 , ∞ ) p(\mu)= N(\mu|0,\infty) p(μ)=N(μ∣0,∞).要注意这也是一个不适当先验(improper prior),因为积分不为1.只要后验适当,使用不适当先验也没问题,也就是有 N ≥ 1 N\ge 1 N≥1个数据点的情况,因为只要有一个单独数据点就可以"确定"区域位置了.
与之类似,也可以对缩放参数(scale parameter)取杰弗里斯先验(Jeffreys prior),比如正态分布的方差, p ( σ 2 ∝ 1 / σ 2 ) p(\sigma^2\propto 1/\sigma^2) p(σ2∝1/σ2).这是一个缩放独立先验(scale invariant prior)满足下面的性质:分配到任意区间[A,B]的概率质量等于分配另一个缩放区间[A/c,B/c]的概率质量,其中的c是某个常数 c > 0 c>0 c>0.(例如,如果将单位从米换成影驰,还不希望影响参数推导过程等等).这可以使用:
p ( s ) ∝ 1 / s p(s)\propto 1/s p(s)∝1/s(5.64)
要注意:
∫ A / c B / c = [ log s ] A / c B / c = log ( B / c ) − log ( A / c ) (5.65) = log ( B ) − log ( A ) = ∫ A B p ( s ) d s (5.66) \begin{aligned} \int ^{B/c}_{A/c}&= [\log s]^{B/c}_{A/c} = \log(B/c)-\log(A/c) &\text{(5.65)}\\ &= \log(B)-\log(A)=\int^B_Ap(s)ds &\text{(5.66)}\\ \end{aligned} ∫A/cB/c=[logs]A/cB/c=log(B/c)−log(A/c)=log(B)−log(A)=∫ABp(s)ds(5.65)(5.66)
可以使用退化 γ \gamma γ分布(degenerate Gamma distribution)来近似,(参考本书2.4.4),即 p ( s ) = G a ( S ∣ 0 , 0 ) p(s)=Ga(S|0,0) p(s)=Ga(S∣0,0).这个先验 p ( s ) ∝ 1 / s p(s)\propto 1/s p(s)∝1/s也是不适当先验,但只要有观测到超过 N ≥ 2 N\ge 2 N≥2个数据点,就能保证后验是适当的,也就可以了.(因为只要最少有两个数据点就可以估计方差了.)
5.4.3 健壮先验(Robust priors)
在很多情况下,我们对先验并不一定很有信心,所以就需要确保先验不会对结果有过多的影响.这可以通过使用健壮先验(robust priors,Insua and Ruggeri 2000)来实现,这种先验通常都有重尾(heavy tailes),这就避免了过分靠近先验均值.
考虑一个来自(Berger 1985,p7)的例子.设x服从正态分布,即 x ∼ N ( θ , 1 ) x\sim N(\theta,1) x∼N(θ,1).观察到了 x=5 然后要去估计 θ \theta θ.最大似然估计(MLE)是 θ ^ = 5 \hat\theta=5 θ^=5,看上去也挺合理.在均匀先验之下的后验均值也是这个值,即 θ ˉ = 5 \bar\theta=5 θˉ=5.不过如果假设我们知道了先验中位数(median)是0,而先验的分位数(quantiles)分别是-1和1,所以就有 p ( θ / l e − 1 ) = p ( − 1 < θ / l e 0 ) = p ( 0 < θ / l e 1 ) = p ( 1 < θ ) = 0.25 p(\theta/le -1)=p(-1<\theta/le 0)=p(0<\theta/le 1)=p(1<\theta)=0.25 p(θ/le−1)=p(−1<θ/le0)=p(0<θ/le1)=p(1<θ)=0.25.另外假设这个先验是光滑单峰的.
很明显正态分布的先验 N ( θ ∣ 0 , 2.1 9 2 ) N(\theta|0,2.19^2) N(θ∣0,2.192)满足这些约束条件.但这时候后验均值就是3.43了,看着就不太让人满意了.
然后再考虑使用柯西分布作先验(Cauchy prior) T ( θ ∣ 0 , 1 , 1 ) T(\theta|0,1,1) T(θ∣0,1,1).这也满足上面的先验约束条件.这次发现用这个先验的话,后验均值就是4.6,看上去就更合理了(计算过程可以用数值积分,参考本书配套的PMTK3当中的 robustPriorDemo中的代码).
5.4.4 共轭先验的混合
健壮先验很有用,不过计算开销太大了.共轭先验可以降低计算难度,但对我们把已知信息编码成先验来说,往往又不够健壮,也不够灵活.不过,共轭先验(conjugate priors)的混合(mixtures)还是共轭的(参考联系5.1),然后还可以对任意一种先验进行近似((Dallal and Hall 1983; Diaconis and Ylvisaker 1985).然后这样的先验就能在计算开销和灵活性之间得到一个很不错的折中.
还以之前抛硬币模型为例,考虑要检查硬币是否作弊,是两面概率都一样,还是有更大概率人头朝上.这就不能用一个 β \beta β分布来表示了.不过可以把它用两个 β \beta β分布的混合来表示.例如,就可以使用:
p ( θ ) = 0.5 B e t a ( θ ∣ 20 , 20 ) + 0.5 B e t a ( θ ∣ 30 , 10 ) p(\theta)=0.5Beta(\theta|20,20)+0.5Beta(\theta|30,10) p(θ)=0.5Beta(θ∣20,20)+0.5Beta(θ∣30,10)(5.67)
如果 θ \theta θ来自第一个分布,就说明没作弊,如果来自第二个分布,就说明有更大概率人头朝上.
可以引入一个潜在指示器变量(latent indicator variable)z来表示这个混合,其中的z=k的意思就是 θ \theta θ来自混合成分(mixture component)k.这样先验的形式就是:
p ( θ ) = ∑ k p ( z = k ) p ( θ ∣ z = k ) p(\theta)=\sum_k p(z=k)p(\theta|z=k) p(θ)=∑kp(z=k)p(θ∣z=k)(5.68)
其中的每个 p ( θ ∣ z = k ) p(\theta|z=k) p(θ∣z=k)都是共轭的,而 p ( z = k ) p(z=k) p(z=k)就叫做先验的混合权重(prior mixing weights).(练习5.1)可知后验也可以写成一系列共轭分布的混合形式:
p ( θ ∣ D ) = ∑ k p ( z = k ) p ( θ ∣ D , z = k ) p(\theta|D)=\sum_k p(z=k)p(\theta|D,z=k) p(θ∣D)=∑kp(z=k)p(θ∣D,z=k)(5.69)
其中的 p ( Z = k ∣ D ) p(Z=k|D) p(Z=k∣D)是后验混合权重(posterior mixing weights),如下所示:
p ( Z = k ∣ D ) = p ( Z = k ) p ( D ∣ Z = k ) ∑ k ′ p ( Z = k ′ ) p ( D ∣ Z = k ′ ) p(Z=k|D)=\frac{p(Z=k)p(D|Z=k)}{\sum_{k'}p(Z=k')p(D|Z=k')} p(Z=k∣D)=∑k′p(Z=k′)p(D∣Z=k′)p(Z=k)p(D∣Z=k)(5.70)
这里的量 p ( D ∣ Z = k ) p(D|Z=k) p(D∣Z=k)是混合成分k的边缘似然函数,可以参考本书5.3.2.1.
5.4.4.1 样例
假如使用下面的混合先验:
p
(
θ
)
=
0.5
B
e
t
a
(
θ
∣
a
1
,
b
1
)
+
0.5
B
e
t
a
(
θ
∣
a
2
,
b
2
)
p(\theta)=0.5Beta(\theta|a_1,b_1)+0.5Beta(\theta|a_2,b_2)
p(θ)=0.5Beta(θ∣a1,b1)+0.5Beta(θ∣a2,b2)(5.71)
其中 a 1 = b 1 = 20 , a 2 = b 2 = 10 a_1=b_1=20,a_2=b_2=10 a1=b1=20,a2=b2=10.然后观察了 N 1 N_1 N1次的人头, N 0 N_0 N0次的背面.后验就成了:
p ( θ ∣ D ) = p ( Z = 1 ∣ D ) B e t a ( θ ∣ a 1 + N 1 , b 1 + N 0 ) + p ( Z = 2 ∣ D ) B e t a ( θ ∣ a 2 + N 1 , b 2 + N 0 ) p(\theta|D)=p(Z=1|D)Beta(\theta|a_1+N_1,b_1+N_0)+p(Z=2|D)Beta(\theta|a_2+N_1,b_2+N_0) p(θ∣D)=p(Z=1∣D)Beta(θ∣a1+N1,b1+N0)+p(Z=2∣D)Beta(θ∣a2+N1,b2+N0)(5.72)
如果 N 1 = 20 , N 0 = 10 N_1=20,N_0=10 N1=20,N0=10,那么使用等式5.23,就得到了后验如下所示:
p ( θ ∣ D ) = 0.346 B e t a ( θ ∣ 40 , 30 ) + 0.654 B e t a ( θ ∣ 50 , 20 ) p(\theta|D)=0.346Beta(\theta|40,30)+0.654Beta(\theta|50,20) p(θ∣D)=0.346Beta(θ∣40,30)+0.654Beta(θ∣50,20)(5.73)
如图5.10是对此的图示.
此处参考原书图5.10

5.4.4.2 应用:在DNA和蛋白质序列中找到保留区域(conserved regions)
之前提到过狄利克雷-多项式模型(Dirichlet-multinomial models)在生物序列分析领域用的很广泛.现在就举个例子来看一下.还要用到本书2.3.2.1当中提到的序列标识(sequence logo).现在假设我们想找到基因中代表了编码区域的位置.这类位置在不同的序列中往往都有同样的字母,这是因为进化原因导致的.所以需要找纯净(pure)或者近似纯净的列(columns),比如都是碱基A/T/C/G当中的一种.一种方法是查找低信息熵的列(low-entropy columns)这些列的分布几乎都是确定的.
然后假设我们相对纯净度都估计的置信程度进行衡量.如果我们认为邻近区域是一同保留的,这就很有用了.这时候设置如果区域t是保留的则 Z t = 1 Z_t=1 Zt=1,反之则 Z t = 0 Z_t=0 Zt=0.可以在临近的 Z t Z_t Zt变量之间加入一个依赖项(dependence),要用一个马尔科夫链(Markov chain),这部分参考本书第17章有详细内容.
无论任何情况,都要定义一个似然率模型(likelihood model) p ( N t ∣ Z t ) p(N_t|Z_t) p(Nt∣Zt),其中的 N t N_t Nt是第t列的(ACGT)碱基计数组成的向量.通常设置这是一个参数为 θ t \theta_t θt的多项式分布.因为每一列(column)都有不同的分布,所以要对 θ t \theta_t θt积分,然后计算边缘似然函数:
p ( N t ∣ Z t ) = ∫ p ( N t ∣ θ t ) p ( θ t ∣ Z t ) d θ t p(N_t|Z_t)=\int p(N_t|\theta_t)p(\theta_t|Z_t)d\theta_t p(Nt∣Zt)=∫p(Nt∣θt)p(θt∣Zt)dθt(5.74)
但是对 θ t \theta_t θt用什么先验呢?当 Z t = 0 Z_t=0 Zt=0的时候可以使用一个均匀显眼,即 p ( θ ∣ Z t = 0 ) = D i r ( 1 , 1 , 1 , 1 ) p(\theta|Z_t=0)=Dir(1,1,1,1) p(θ∣Zt=0)=Dir(1,1,1,1),可是如果 Z t = 1 Z_t=1 Zt=1呢?如果一列被保留了,就应该是纯粹(或者近似纯粹)由ACGT四种碱基中的一种组成的.很自然的方法就是使用狄利克雷先验的混合,每一个都朝向四维单形(simplex)中的一角倾斜(tilted),即:
p ( θ ∣ Z t = 1 ) = 1 4 D i r ( θ ∣ ( 10 , 1 , 1 , 1 ) ) + . . . + 1 4 D o r ( θ ∣ ( 1 , 1 , 1 , 10 ) ) p(\theta|Z_t=1)=\frac14Dir(\theta|(10,1,1,1))+...+\frac14Dor(\theta|(1,1,1,10)) p(θ∣Zt=1)=41Dir(θ∣(10,1,1,1))+...+41Dor(θ∣(1,1,1,10))(5.75)
由于这也是共轭的,所以 p ( N t ∣ Z t ) p(N_t|Z_t) p(Nt∣Zt)计算起来很容易.参考(Brown et al. 1993)来查看一个在现实生物序列问题中的具体应用.
5.5 分层贝叶斯(Hierarchical Bayes)
计算后验
p
(
θ
∣
D
)
p(\theta|D)
p(θ∣D)的一个关键要求就是特定的先验
p
(
θ
∣
η
)
p(\theta|\eta)
p(θ∣η),其中的
η
\eta
η是超参数(hyper-parameters).如果不知道怎么去设置
η
\eta
η咋办呢?有的时候可以使用无信息先验,之前已经说过了.一个更加贝叶斯风格的方法就是对先验设一个先验!用本书第十章的图模型的术语来说,可以用下面的方式来表达:
η
→
θ
→
D
\eta \rightarrow \theta \rightarrow D
η→θ→D(5.76)
这就是一个分层贝叶斯模型(hierarchical Bayesian model),也叫作多层模型(multi-level model),因为有多层的未知量.下面给一个简单样例,后文还会有更多其他的例子.
5.5.1 样例:与癌症患病率相关的模型
考虑在不同城市预测癌症患病率的问题(这个样例来自Johnson and Albert 1999, p24).具体来说,加入我们要测量不同城市的人口, N i N_i Ni,然后对应城市死于癌症的人口数 x i x_i xi.假设 x i ∼ B i n ( N i , θ i ) x_i\sim Bin(N_i,\theta_i) xi∼Bin(Ni,θi),然后要估计癌症发病率 θ i \theta_i θi.一种方法是分别进行估计,不过这就要面对稀疏数据问题(低估了人口少即 N i N_i Ni小的城市的癌症发病率).另外一种方法是假设所有的 θ i \theta_i θi都一样;这叫做参数绑定(parameter tying.结果得到的最大似然估计(MLE)正好就是 θ ^ = Σ i x i Σ i N i \hat\theta =\frac{\Sigma_ix_i}{\Sigma_iN_i} θ^=ΣiNiΣixi.可是很明显假设所有城市癌症发病率都一样有点太牵强了.有一种折中的办法,就是估计 θ i \theta_i θi是相似的,但可能随着每个城市的不同而又发生变化.这可以通过假设 θ i \theta_i θi服从某个常见分布来实现,比如 β \beta β分布,即 θ i ∼ B e t a ( a , b ) \theta_i\sim Beta(a,b) θi∼Beta(a,b).这样就可以把完整的联合分布写成下面的形式:
p ( D , θ , η ∣ N ) = p ( η ) ∏ i = 1 N B i n ( x i ∣ N i , θ i ) B e t a ( θ i ∣ η ) p(D,\theta,\eta|N)=p(\eta)\prod^N_{i=1}Bin(x_i|N_i,\theta_i)Beta(\theta_i|\eta) p(D,θ,η∣N)=p(η)∏i=1NBin(xi∣Ni,θi)Beta(θi∣η)(5.77)
上式中的 η = ( a , b ) \eta=(a,b) η=(a,b).要注意这里很重要的一点是要从数据中推测 η = ( a , b ) \eta=(a,b) η=(a,b);如果只是随便设置成一个常数,那么 θ i \theta_i θi就会是有件独立的(conditionally independent),在彼此之间就没有什么信息联系了.与之相反的,若将 η \eta η完全看做一个未知量(隐藏变量),就可以让数据规模小的城市从数据规模大的城市借用统计强度(borrow statistical strength).
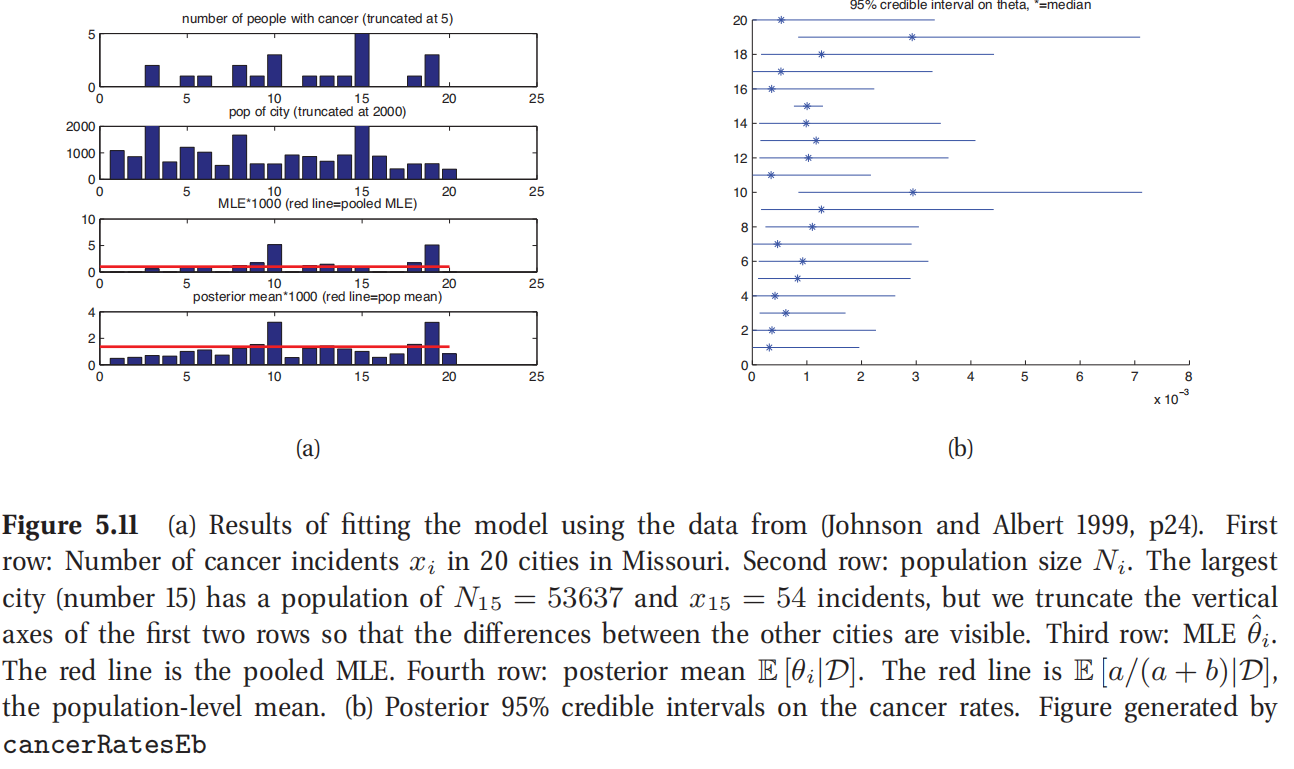
要计算联合后验 p ( η , θ ∣ D ) p(\eta,\theta|D) p(η,θ∣D).从这里面可以得到后验边缘分布 p ( θ i ∣ D ) p(\theta_i|D) p(θi∣D).如图5.11(a)所示,图中的蓝色柱状是后验均值 E [ θ i ∣ D ] E[\theta_i|D] E[θi∣D],红色线条是城市人口均值 E [ a / ( a + b ∣ D ] E[a/(a+b_|D] E[a/(a+b∣D](这代表了 θ i \theta_i θi的均值).很明显可以看到后验均值朝向有小样本 N i N_i Ni的城市的汇总估计方向收缩.例如,城市1和城市20都观察到有0的癌症发病率,但城市20的人口数较少,所以其癌症发病率比城市1更朝向人口估计方向收缩(也就是距离水平的红色线更近).
图5.11(b)展示的是 θ i \theta_i θi的95%后验置信区间.可以看到城市15有特别多的人口(53637),后验不确定性很低.所以这个城市对 η \eta η的后验估计的影响最大,也会影响其他城市的癌症发病率的估计.城市10和19有最高的最大似然估计(MLE),也有最高的后验不确定性,反映了这样高的估计可能和先验相违背(先验视从所有其他城市估计得到的).
上面这个例子中,每个城市都有一个参数,然后对相应的概率进行建模.通过设置伯努利分布的频率参数为一个协变量的函数,即 θ i = s i g m ( w i T x ) \theta_i=sigm(w^T_ix) θi=sigm(wiTx),就可以对多个相关的逻辑回归任务进行建模了.这也叫做多任务学习(multi-task learning),在本书9.5会有详细讲解.
5.6 经验贝叶斯(Empirical Bayes)
在分层贝叶斯模型中,我们需要计算多层的潜在变量的后验.例如,在一个两层模型中,需要计算:
p
(
η
,
θ
∣
D
)
∝
p
(
D
∣
θ
)
p
(
θ
∣
η
)
p
(
η
)
p(\eta,\theta|D)\propto p(D|\theta)p(\theta|\eta)p(\eta)
p(η,θ∣D)∝p(D∣θ)p(θ∣η)p(η)(5.78)
有的时候可以通过分析将 θ \theta θ边缘化;这就将问题简化成只去计算 p ( η ∣ D ) p(\eta|D) p(η∣D)了.
作为计算上的简化,可以对超参数后验进行点估计来近似,即 p ( η ∣ D ) ≈ δ η ^ ( η ) p(\eta|D)\approx \delta_{\hat\eta}(\eta) p(η∣D)≈δη^(η),其中的 η ^ = arg max p ( η ∣ D ) \hat\eta=\arg\max p(\eta|D) η^=argmaxp(η∣D).因为 η \eta η通常在维数上都比 θ \theta θ小很多,这个模型不太容易过拟合,所以我们可以安全地来对 η \eta η使用均匀显眼.这样估计就成了:
η ^ = arg max p ( D ∣ η ) = arg max [ ∫ p ( D ∣ θ ) p ( θ ∣ η ) d θ ] \hat\eta =\arg\max p(D|\eta)=\arg\max[\int p(D|\theta)p(\theta|\eta)d\theta] η^=argmaxp(D∣η)=argmax[∫p(D∣θ)p(θ∣η)dθ](5.79)
其中括号里面的量就是边缘似然函数或整合似然函数(marginal or integrated likelihood),也叫证据(evidence).这个方法总体上叫做经验贝叶斯(Empirical Bayes,缩写为EB)或这也叫座第二类最大似然估计(Type II Maximum Likelihood).在机器学习里面,也叫作证据程序(evidence procedure).
经验贝叶斯违反了先验应该独立于数据来选择的原则.不过可以将其视作是对分层贝叶斯模型中的推导的一种近似,计算开销更低.就好比是讲最大后验估计(MAP estimation)看作是对单层模型 θ → D \theta\rightarrow D θ→D的推导的近似一样.实际上,可以建立一个分层结构,其中进行的积分越多,就越"贝叶斯化":
| 方法(Method) | 定义(Definition) |
|---|---|
| 最大似然估计(Maximum Likelihood) | $\hat\theta=\arg\max_\theta p(D |
| 最大后验估计(MAP estimation) | $\hat\theta=\arg\max_\theta p(D |
| 经验贝叶斯的最大似然估计(ML-II Empirical Bayes) | $\hat\theta=\arg\max_\eta \int p(D |
| 经验贝叶斯的最大后验估计(MAP-II) | $\hat\theta=\arg\max_\eta \int p(D |
| 全贝叶斯(Full Bayes) | $p(\theta,\eta |
要注意,经验贝叶斯(EB)也有很好的频率论解释(参考Carlin and Louis 1996; Efron 2010),所以在非贝叶斯模型中也被广泛使用.例如很流行的詹姆斯-斯坦因估计器(James-Stein estimator)就是用经验贝叶斯推导的,更多细节参考本书6.3.3.2.
5.6.1 样例: β \beta β-二项模型
还回到癌症发病率的模型上.可以积分掉 θ i \theta_i θi,然后直接写出边缘似然函数,如下所示:
p ( D ∣ a , b ) = ∏ i ∫ B i n ( x i ∣ N i , θ i ) B e t a ( θ i ∣ a , b ) d θ i (5.80) = ∏ i B ( a + x i , b + N i − x i ) B ( a , b ) ( ( 5.81 ) ) \begin{aligned} p(D|a,b)&=\prod_i \int Bin(x_i|N_i,\theta_i)Beta(\theta_i|a,b)d\theta_i & \text{(5.80)}\\ &=\prod_i \frac{B(a+x_i,b+N_i-x_i)}{B(a,b)} & \text((5.81))\\ \end{aligned} p(D∣a,b)=i∏∫Bin(xi∣Ni,θi)Beta(θi∣a,b)dθi=i∏B(a,b)B(a+xi,b+Ni−xi)(5.80)((5.81))
关于a和b来最大化有很多方法,可以参考(Minka 2000e).
估计完了a和b之后,就可以代入到超参数里面来计算后验分布 p ( θ i ∣ a ^ , b ^ , D ) p(\theta_i|\hat a,\hat b,D) p(θi∣a^,b^,D),还按照之前的方法,使用共轭分析.得到的每个 θ i \theta_i θi的后验均值就是局部最大似然估计(local MLE)和先验均值的加权平均值,依赖于 η = ( a , b ) \eta=(a,b) η=(a,b);但由于 η \eta η是根据所有数据来估计出来的,所以每个 θ i \theta_i θi也都受到全部数据的影响.
5.6.2 样例:高斯-高斯模型(Gaussian-Gaussian model)
接下来这个例子和癌症发病率的例子相似,不同之处是这个例子中的数据是实数值的(real-valued).使用一个高斯(正态)似然函数(Gaussian likelihood)和一个高斯(正态)先验(Gaussian prior).这样就能写出来解析形式的解.
设我们有来自多个相关群体的数据.比如 x i j x_{ij} xij表示的就是学生i在学校j得到的测试分数,j的取值范围从1到D,而i是从1到 N j N_j Nj,即 j = 1 : D , i = 1 : N j j=1:D,i=1:N_j j=1:D,i=1:Nj.然后想要估计每个学校的平均分 θ j \theta_j θj.可是样本规模 N j N_j Nj对于一些学校来说可能很小,所以可以用分层贝叶斯模型(hierarchical Bayesian model)来规范化这个问题,也就是假设 θ j \theta_j θj来自一个常规的先验(common prior) N ( μ , τ 2 ) N(\mu,\tau^2) N(μ,τ2).
这个联合分布的形式如下所示:
p
(
θ
,
D
∣
η
,
σ
2
)
=
∏
j
=
1
D
N
(
θ
j
∣
μ
,
τ
2
)
∏
i
=
1
N
j
N
(
x
i
j
∣
θ
j
,
σ
2
)
p(\theta,D|\eta,\sigma^2)=\prod^D_{j=1}N(\theta_j|\mu,\tau^2)\prod^{N_j}_{i=1}N(x_{ij}|\theta_j,\sigma^2)
p(θ,D∣η,σ2)=∏j=1DN(θj∣μ,τ2)∏i=1NjN(xij∣θj,σ2)(5.82)
上式中为了简化,假设了 σ 2 \sigma^2 σ2是已知的.(这个假设在练习24.4中.)接下来将估计 η \eta η.一旦估计了 η = ( μ , τ ) \eta=(\mu,\tau) η=(μ,τ),就可以计算 θ j \theta_j θj的后验了.要进行这个计算,只需要将联合分布改写成下面的形式,这个过程利用值 x i j x_{ij} xij和方差为 σ 2 \sigma^2 σ2的 N j N_j Nj次高斯观测等价于值为 x ˉ j = △ 1 N j ∑ i = 1 N j x i j \bar x_j \overset\triangle{=} \frac{1}{N_j}\sum^{N_j}_{i=1}x_{ij} xˉj=△Nj1∑i=1Njxij方差为 σ j 2 = △ σ 2 / N j \sigma^2_j\overset\triangle{=}\sigma^2/N_j σj2=△σ2/Nj的一次观测这个定理.这就得到了:
p ( θ , D ∣ η ^ , σ 2 ) = ∏ j = 1 D N ( θ j ∣ μ ^ , τ ^ 2 ) N ( x ˉ j ∣ θ j , σ j 2 ) p(\theta,D|\hat\eta,\sigma^2)=\prod^D_{j=1}N(\theta_j|\hat\mu,\hat\tau^2)N(\bar x_j|\theta_j,\sigma^2_j) p(θ,D∣η^,σ2)=∏j=1DN(θj∣μ^,τ^2)N(xˉj∣θj,σj2)(5.83)
利用上面的式子,再利用本书4.4.1当中的结论,就能得到后验为:
p ( θ j ∣ D , μ ^ , τ ^ 2 ) = N ( θ j ∣ B ^ j μ ^ + ( 1 − B ^ j ) x ˉ j , ( 1 − B ^ j ) σ j 2 ) (5.84) B ^ j = △ σ j 2 σ j 2 + τ ^ 2 (5.85) \begin{aligned} p(\theta_j|D,\hat\mu,\hat\tau^2)&= N(\theta_j|\hat B_j\hat\mu+(1-\hat B_j)\bar x_j,(1-\hat B_j)\sigma^2_j) \text{(5.84)}\\ \hat B_j &\overset\triangle{=} \frac{\sigma^2_j}{\sigma^2_j+\hat\tau^2}\text{(5.85)}\\ \end{aligned} p(θj∣D,μ^,τ^2)B^j=N(θj∣B^jμ^+(1−B^j)xˉj,(1−B^j)σj2)(5.84)=△σj2+τ^2σj2(5.85)
其中的 μ ^ = x ˉ , τ ^ 2 \hat\mu =\bar x,\hat\tau^2 μ^=xˉ,τ^2下面会给出定义.
0 ≤ B ^ j ≤ 1 0\le \hat B_j \le 1 0≤B^j≤1这个量控制了朝向全局均值(overall mean) μ \mu μ的收缩程度(degree of shrinkage).如果对于第j组来说数据可靠(比如可能是样本规模 N j N_j Nj特别大),那么 σ j 2 \sigma^2_j σj2就会比 τ 2 \tau^2 τ2小很多;因此这样 B ^ j \hat B_j B^j也会很小,然后就会在估计 θ j \theta_j θj的时候给 x ˉ j \bar x_j xˉj更多权重.而样本规模小的群组就会被规范化(regularized),也就是朝向全局均值 μ \mu μ的方向收缩更严重.接下来会看到一个例子.
如果对于所有的组j来说都有
σ
j
=
σ
\sigma_j=\sigma
σj=σ,那么后验均值就成了:"
θ
^
j
=
B
^
x
ˉ
+
(
1
−
B
^
)
x
ˉ
j
=
x
ˉ
+
(
1
−
B
^
)
(
x
ˉ
j
−
x
ˉ
)
\hat\theta_j= \hat B\bar x+(1-\hat B)\bar x_j=\bar x +(1-\hat B)(\bar x_j-\bar x)
θ^j=B^xˉ+(1−B^)xˉj=xˉ+(1−B^)(xˉj−xˉ)(5.86)
这和本书在6.3.3.2中讨论到的吉姆斯-斯坦因估计器(James Stein estimator)的形式一模一样.
5.6.2.1 样例:预测棒球得分
接下来这个例子是把上面的收缩(shrinkage)方法用到棒球击球平均数(baseball batting averages, 引自 Efron and Morris 1975).观察D=18个球员在前T=45场比赛中的的击球次数.把这个击球次数设为 b i b_i bi.假设服从二项分布,即 b j ∼ B i n ( T , θ j ) b_j\sim Bin(T,\theta_j) bj∼Bin(T,θj),其中的 θ j \theta_j θj是选手j的"真实"击球平均值.目标是要顾及出来这个 θ j \theta_j θj.最大似然估计(MLE)自然是 θ ^ j = x j \hat\theta_j=x_j θ^j=xj,其中的 x j = b j / T x_j=b_j/T xj=bj/T是经验击球平均值.不过可以用经验贝叶斯方法来进行更好的估计.
要使用上文中讲的高斯收缩方法(Gaussian shrinkage approach),需要似然函数是高斯分布的,即对于一直的 σ 2 \sigma^2 σ2有 x j ∼ N ( θ j , σ 2 ) x_j\sim N(\theta_j,\sigma^2) xj∼N(θj,σ2).(这里去掉了下标i因为假设了 N j = 1 N_j=1 Nj=1而 x j x_j xj已经代表了选手j的平均值了.)不过这个例子里面用的是二项似然函数.均值正好是 E [ x j ] = θ j E[x_j]=\theta_j E[xj]=θj,方差则是不固定的:
v a r [ x j ] = 1 T 2 v a r [ b j ] = T θ j ( 1 − θ j ) T 2 var[x_j]=\frac{1}{T^2}var[b_j]=\frac{T\theta_j(1-\theta_j)}{T^2} var[xj]=T21var[bj]=T2Tθj(1−θj)(5.87)
所以咱们对
x
j
x_j
xj应用一个方差稳定变换(variance stabilizing transform 5)来更好地符合高斯假设:
y
i
=
f
(
y
i
)
=
T
arcsin
(
2
y
i
−
1
)
y_i=f(y_i)=\sqrt{T}\arcsin (2y_i-1)
yi=f(yi)=Tarcsin(2yi−1)(5.88)
然后应用一个近似 y i ∼ N ( f ( θ j ) , 1 ) = N ( μ j , 1 ) y_i\sim N(f(\theta_j),1)=N(\mu_j,1) yi∼N(f(θj),1)=N(μj,1).以 σ 2 = 1 \sigma^2=1 σ2=1代入等式5.86来使用高斯收缩对 μ j \mu_j μj进行估计,然后变换回去,就得到了:
θ ^ j = 0.5 ( sin ( μ ^ j / T ) + 1 ) \hat\theta_j=0.5(\sin(\hat\mu_j/\sqrt{T})+1) θ^j=0.5(sin(μ^j/T)+1)(5.89)
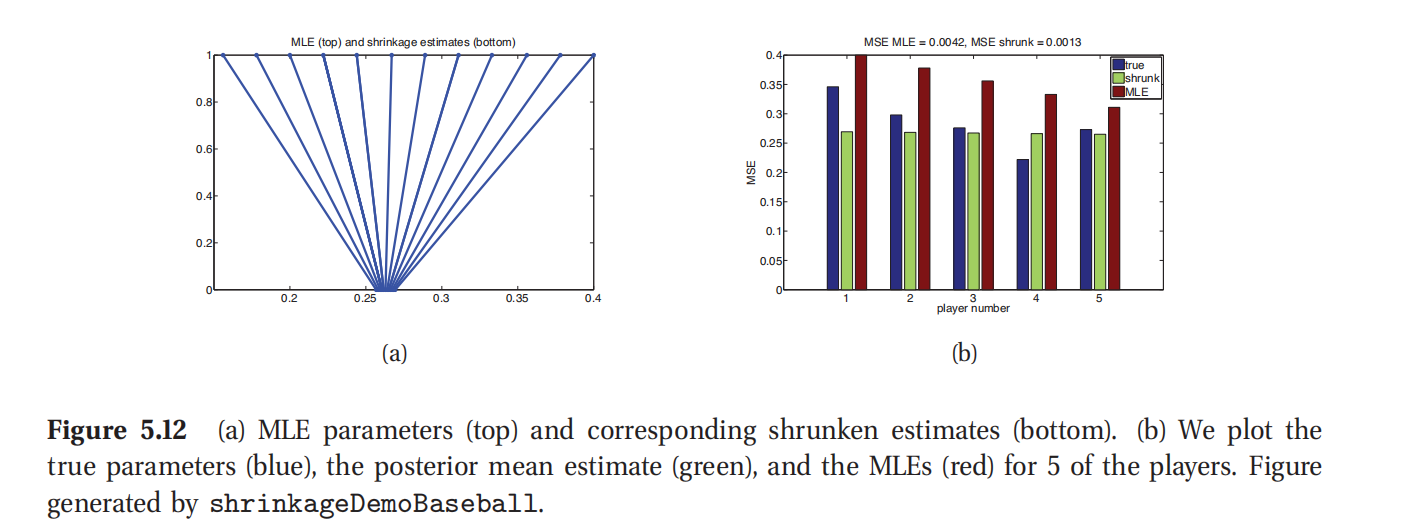
此处参考原书图5.12
这个结果如图5.12(a-b)所示.在图(a)中,投图的是最大似然估计(MLE) θ ^ j \hat\theta_j θ^j和后验均值 θ ˉ j \bar\theta_j θˉj.可以看到所有的估计都朝向全局均值0.265收缩.在图(b)中,投图的是 θ j \theta_j θj的真实值,最大似然估计(MLE) θ ^ j \hat\theta_j θ^j和后验均值 θ ˉ j \bar\theta_j θˉj.(这里的 θ j \theta_j θj的真实值是指从更大规模的独立赛事之间得到的估计值.)可以看到平均来看,收缩的估计比最大似然估计(MLE)更加靠近真实值.尤其是均方误差,定义为 M S E = 1 N ∑ j = 1 D ( θ j − θ ˉ j ) 2 MSE=\frac{1}{N}\sum^D_{j=1}(\theta_j-\bar\theta_j)^2 MSE=N1∑j=1D(θj−θˉj)2,使用收缩估计的 θ ˉ j \bar\theta_j θˉj比最大似然估计的 θ ^ j \hat\theta_j θ^j的均方误差小了三倍.
5.6.2.2 估计超参数
在本节会对估计
η
\eta
η给出一个算法.加入最开始对于所有组来说都有
σ
j
2
=
σ
2
\sigma^2_j=\sigma^2
σj2=σ2.这种情况下就可以以闭合形式(closed form)来推导经验贝叶斯估计(EB estimate).从等式4.126可以得到:
p
(
x
ˉ
j
∣
μ
,
τ
2
,
σ
2
)
=
∫
N
(
x
ˉ
j
∣
θ
j
,
σ
2
)
N
(
θ
j
∣
μ
,
τ
2
)
d
θ
j
=
N
(
x
ˉ
j
∣
μ
,
τ
2
+
σ
2
)
p(\bar x_j|\mu,\tau^2,\sigma^2)=\int N(\bar x_j|\theta_j,\sigma^2)N(\theta_j|\mu,\tau^2)d\theta_j =N(\bar x_j|\mu,\tau^2+\sigma^2)
p(xˉj∣μ,τ2,σ2)=∫N(xˉj∣θj,σ2)N(θj∣μ,τ2)dθj=N(xˉj∣μ,τ2+σ2)(5.90)
然后边缘似然函数(marginal likelihood)为:
p ( D ∣ μ , τ 2 , σ 2 ) = ∏ j = 1 D N ( x ˉ j ∣ μ , τ 2 + σ 2 ) p(D|\mu,\tau^2,\sigma^2)=\prod^D_{j=1}N(\bar x_j|\mu,\tau^2+\sigma^2) p(D∣μ,τ2,σ2)=∏j=1DN(xˉj∣μ,τ2+σ2)(5.91)
接下来就可以使用对正态分布(高斯分布)的最大似然估计(MLE)来估计超参数了.例如对 μ \mu μ就有:
μ ^ = 1 D ∑ j = 1 D x ˉ j = x ˉ \hat \mu =\frac{1}{D}\sum^D_{j=1}\bar x_j=\bar x μ^=D1∑j=1Dxˉj=xˉ(5.92)
上面这个也就是全局均值.
对于方差,可以使用矩量匹配(moment matching,相当于高斯分布的最大似然估计):简单地把模型方差(model varianc)等同于经验方差(empirical variance):
τ ^ 2 + σ 2 = 1 D ∑ j ] 1 D ( x ˉ j − x ˉ ) 2 = △ s 2 \hat \tau^2+\sigma^2 =\frac{1}{D}\sum^D_{j]1}(\bar x_j-\bar x)^2\overset\triangle{=} s^2 τ^2+σ2=D1∑j]1D(xˉj−xˉ)2=△s2(5.93)
所以有 τ ^ 2 = s 2 − σ 2 \hat \tau^2=s^2-\sigma^2 τ^2=s2−σ2.因为已知了 τ 2 \tau^2 τ2必然是正的,所以通常都使用下面这个修订过的估计:
τ ^ 2 = max ( 0 , s 2 − σ 2 ) = ( s 2 − σ 2 ) + \hat \tau^2=\max(0,s^2-\sigma^2)=(s^2-\sigma^2)_{+} τ^2=max(0,s2−σ2)=(s2−σ2)+(5.94)
这样就得到了收缩因子(shrinkage factor):
B ^ = σ 2 σ 2 + τ 2 = σ 2 σ 2 + ( s 2 − σ 2 ) + \hat B=\frac{\sigma^2}{\sigma^2+\tau^2}=\frac{\sigma^2}{\sigma^2+(s^2-\sigma^2)_{+}} B^=σ2+τ2σ2=σ2+(s2−σ2)+σ2(5.95)
如果 σ j 2 \sigma^2_j σj2各自不同,就没办法以闭合形式来推导出解了.练习11.13讨论的是如何使用期望最大化算法(EM algorithm)来推导一个经验贝叶斯估计(EB estimate),练习24.4讨论了如何在这个分层模型中使用全贝叶斯方法.
5.7 贝叶斯决策规则(Bayesian decision rule)
之前的内容中,我们已经看到了概率理论可以用来表征和更新我们对客观世界状态的信念.不过我们最终目标是把信念转化成行动.在本节,讲的就是用最有方法来实现这个目的.
我们可以把任何给定的统计决策问题规范表达成一个与自然客观世界作为对手的游戏(而不是和其他的玩家相对抗,和玩家对抗就是博弈论范畴了,可以参考Shoham and Leyton-Brown 2009).在这个游戏中,自然客观世界会选择一个状态/参数/标签, y ∈ Y y\in Y y∈Y,对我们来说是未知的,然后生成了一次观察 x ∈ X x\in X x∈X,这是我们看到的.接下来我们就要做出一次决策(decision),也就是要从某个行为空间(action space)中选择一个行动a.最终会得到某种损失(loss), L ( y , a ) L(y,a) L(y,a),这个损失函数测量了咱们选择的行为a和自然客观世界隐藏的状态y之间的兼容程度.例如,可以使用误分类损失(misclassitication loss) L ( y , a ) = I ( y ≠ a ) L(y,a)= I(y\ne a) L(y,a)=I(y=a),或者用平方误差损失(squared loss) L ( y , a ) = ( y − a ) 2 L(y,a)=(y-a)^2 L(y,a)=(y−a)2.接下来是一些其他例子.
我们的目标就是设计一个决策程序或者决策策略(decision procedure or policy) δ : X → A \delta:X\rightarrow A δ:X→A,对每个可能的输入指定了最优行为.这里的优化(optimal)的意思就是让行为能够使损失函数期望最小:
δ ( x ) = arg min a ∈ A E [ L ( y , a ) ] \delta(x)=\arg\min_{a\in A} E[L(y,a)] δ(x)=argmina∈AE[L(y,a)](5.96)
在经济学领域,更常见的属于是效用函数(utility function),其实也就是损失函数取负值,即 U ( y , a ) = − L ( y , a ) U(y,a)=-L(y,a) U(y,a)=−L(y,a).这样上面的规则就成了:
δ ( x ) = arg max a ∈ A E [ U ( y , a ) ] \delta(x)=\arg\max_{a\in A} E[U(y,a)] δ(x)=argmaxa∈AE[U(y,a)](5.97)
这就叫期望效用最大化规则(maximum expected utility principle),是所谓理性行为(rational behavior)的本质.
这里要注意"期望(expected)"这个词,是可以有两种理解的.在贝叶斯统计学语境中的意思是给定了已经看到的数据之后,对y的期望值(expected value)后面也会具体讲.在频率论统计学语境中,意思是我们期待在未来看到y和x的期望值,具体会在本书6.3当中讲解.
在贝叶斯决策理论的方法中,观察了x之后的最优行为定义是能后让后验期望损失(posterior expected loss)最小的行为.
ρ ( a ∣ x ) = △ E p ( y ∣ x ) [ L ( y , a ) ] = ∑ y L ( y , a ) p ( y ∣ x ) \rho(a|x)\overset\triangle{=} E_{p(y|x)} [L(y,a)]=\sum_y L(y,a)p(y|x) ρ(a∣x)=△Ep(y∣x)[L(y,a)]=∑yL(y,a)p(y∣x)(5.98)
(如果y是连续的,比如想要估计一个参数向量的时候,就应该把上面的求和替换成为积分.)这样就有了贝叶斯估计器(Bayes estimator),也叫做贝叶斯决策规则(Bayes decision rule):
δ ( x ) = arg min a ∈ A ρ ( a ∣ x ) \delta(x)=\arg\min_{a\in A}\rho(a|x) δ(x)=argmina∈Aρ(a∣x)(5.99)
5.7.1 常见损失函数的贝叶斯估计器
这一节我们展示了对一些机器学习中常遇到的损失函数如何构建贝叶斯估计器.
5.7.1.1 最大后验估计(MAP estimate)最小化0-1损失
0-1损失(0-1 loss)的定义是:
L
(
y
,
a
)
=
I
(
y
≠
a
)
=
{
0
if
a
=
y
1
if
a
≠
y
L(y,a)=I(y\ne a)=\begin{cases} 0 &\text{if} &a=y\\ 1 &\text{if} &a\ne y\end{cases}
L(y,a)=I(y=a)={01ififa=ya=y(5.100)
这通常用于分类问题中,其中的y是真实类标签(true class label),而 a = y ^ a=\hat y a=y^是估计得到的类标签.
例如,在二分类情况下,可以写成下面的损失矩阵(loss matrix):
| \hat y=1 | \hat y=0 | |
|---|---|---|
| y=1 | 0 | 1 |
| y=0 | 1 | 0 |
此处查看原书图master/Figure/5.13
(在本书5.7.2,会把上面这个损失函数进行泛化,就可以应用到对偏离对角位置的两种错误的惩罚上了.)
后验期望损失为:
ρ ( a ∣ x ) = p ( a ≠ y ∣ x ) = 1 − p ( y ∣ x ) \rho(a|x)=p(a\ne y|x)=1-p(y|x) ρ(a∣x)=p(a=y∣x)=1−p(y∣x)(5.101)
所以能够最小化期望损失的行为就是后验众数(posterior mode)或者最大后验估计(MAP estimate):
y △ ( x ) = arg max y ∈ Y p ( y ∣ x ) y^\triangle(x)=\arg\max_{y\in Y} p(y|x) y△(x)=argmaxy∈Yp(y∣x)(5.102)
5.7.1.2 拒绝选项(Reject option)
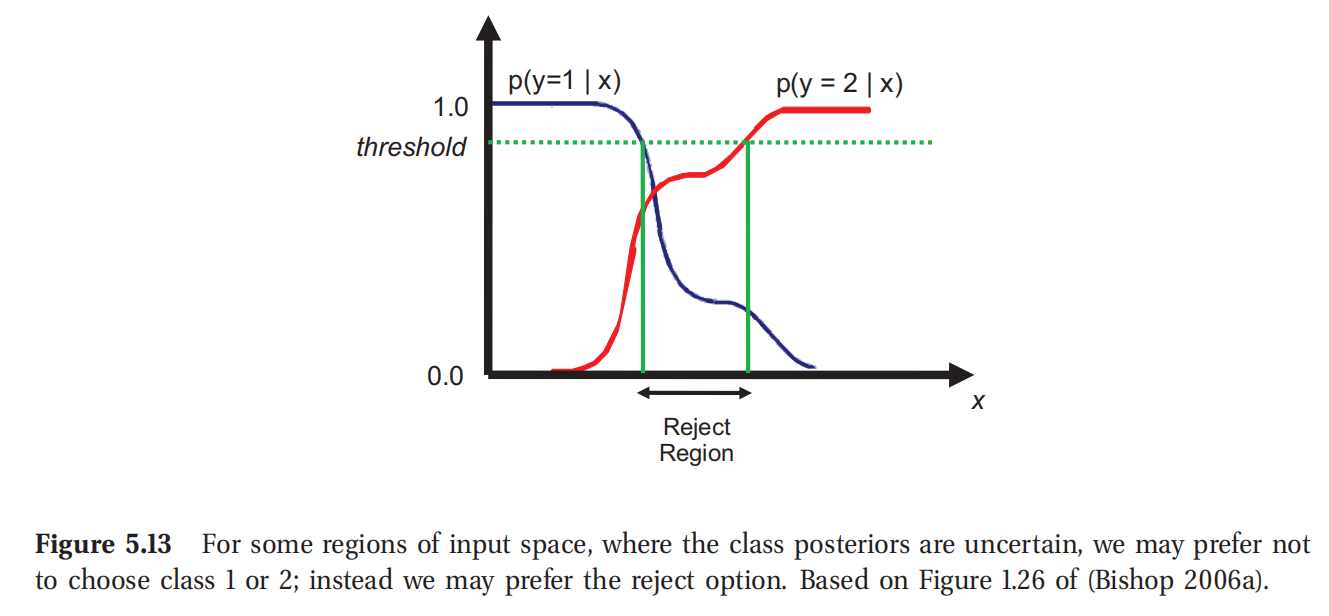
在分类问题中, p ( y ∣ x ) p(y|x) p(y∣x)是非常不确定的,所以我们可能更倾向去选择一个拒绝行为(reject action),也就是拒绝将这个样本分类到任何已有的指定分类中,而是告知"不知道".这种模糊情况可以被人类专家等来处理,比如图5.13所示.对于风险敏感的领域(risk averse domains)比如医疗和金融等,这是很有用处的.
接下来讲这个拒绝选项用正规化语言表达一下.设选择一个 a = C + 1 a=C+1 a=C+1对应的就是选择了拒绝行为,然后选择 a ∈ { 1 , . . . , C } a\in \{1,...,C\} a∈{1,...,C}对应的就是分类到类标签中去.然后就可以定义下面的损失函数:
L ( y = j , a = i ) = { 0 if i = j i , j ∈ { 1 , . . . , C } λ r if i = C + 1 λ s otherwise L(y=j,a=i)=\begin{cases} 0 &\text{if} &i=j & i,j \in\{1,...,C\}\\ \lambda_r &\text{if} &i=C+1 \\ \lambda_s &\text{otherwise}\end{cases} L(y=j,a=i)=⎩ ⎨ ⎧0λrλsififotherwisei=ji=C+1i,j∈{1,...,C}(5.103)
此处查看原书图master/Figure/5.14
5.7.1.3 后验均值(Posterior mean)最小化 l 2 l_2 l2(二次)损失函数
对于连续参数,更适合使用的损失函数是平方误差函数(squared error),也成为 l 2 l_2 l2损失函数,或者叫二次损失函数(quadratic loss),定义如下:
L
(
y
,
a
)
=
(
y
−
a
)
2
L(y,a)=(y-a)^2
L(y,a)=(y−a)2(5.104)
后验期望损失为:
ρ ( a ∣ x ) = E [ ( y − a ) 2 ∣ x ∣ ] = E [ y 2 ∣ x ] − 2 a E [ y ∣ x ] + a 2 \rho(a|x)=E[(y-a)^2|x|]=E[y^2|x]-2aE[y|x]+a^2 ρ(a∣x)=E[(y−a)2∣x∣]=E[y2∣x]−2aE[y∣x]+a2(5.105)
这样最优估计就是后验均值:
∂ ∂ a ρ ( a ∣ x ) = − 2 E [ y ∣ x ] + 2 a = 0 ⟹ y ^ = E [ y ∣ x ] = ∫ y p ( y ∣ x ) d y \frac{\partial}{\partial a}\rho(a|x)= -2E[y|x]+2a=0 \Longrightarrow \hat y=E[y|x]=\int y p(y|x)dy ∂a∂ρ(a∣x)=−2E[y∣x]+2a=0⟹y^=E[y∣x]=∫yp(y∣x)dy(5.106)
这也叫做最小均值方差估计(minimum mean squared error,缩写为MMSE).
在线性回归问题中有:
p ( y ∣ x , θ ) = N ( y ∣ x T w , σ 2 ) p(y|x,\theta)=N(y|x^Tw,\sigma^2) p(y∣x,θ)=N(y∣xTw,σ2)(5.107)
这时候给定某个训练集D之后的最优估计就是:
E [ y ∣ x , D ] = x T E [ w ∣ D ] E[y|x,D]=x^TE[w|D] E[y∣x,D]=xTE[w∣D](5.108)
也就是将后验均值参数估计代入.注意不论对w使用什么样的先验,这都是最优选择.
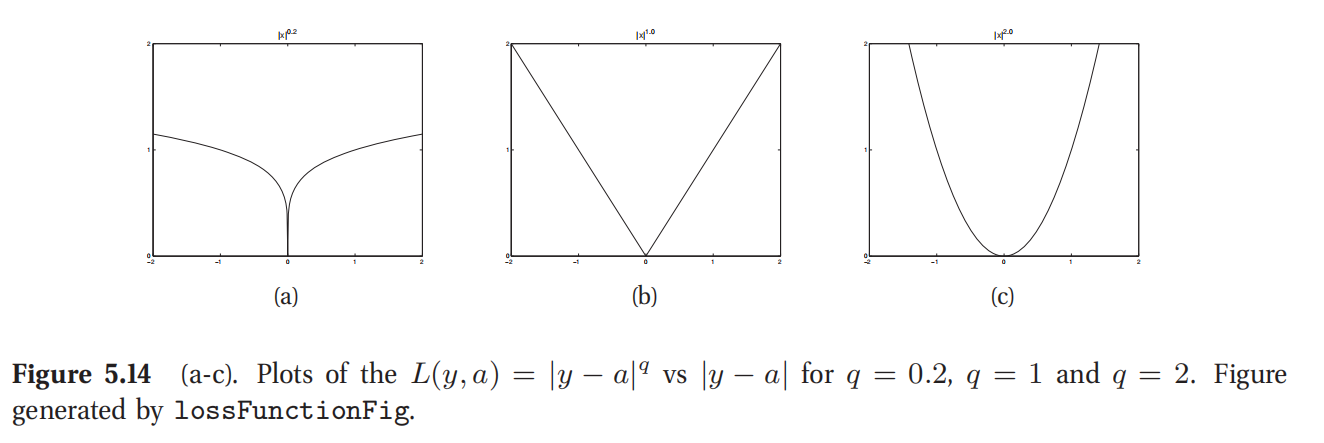
5.7.1.4 后验中位数(Posterior median)最小化 l 1 l_1 l1(绝对)损失函数
l 2 l_2 l2(二次)损失函数以二次形式惩罚与真实值的偏离,因此对异常值(outliers)特别敏感.所以有一个更健壮的替换选择,就是绝对损失函数,或者也叫做 l 1 l_1 l1损失函数 L ( y , a ) = ∣ y − a ∣ L(y,a)=|y-a| L(y,a)=∣y−a∣(如图5.14所示).这里的最优估计就是后验中位数,也就是使得 P ( y < a ∣ x ) = P ( y ≥ a ∣ x ) = 0.5 P(y < a|x) = P(y \ge a|x) = 0.5 P(y<a∣x)=P(y≥a∣x)=0.5的a值,具体证明参考本书练习5.9.
5.7.1.5 监督学习(Supervised learning)
设想有一个预测函数 δ : X → Y \delta: X\rightarrow Y δ:X→Y,然后设有某个损失函数 l ( y , y ′ ) l(y,y') l(y,y′),这个损失函数给出了预测出 y ′ y' y′而真实值是 y y y的时候的损失.这样就可以定义采取行为 δ \delta δ(比如使用这个预测器)而未知自然状态为 θ \theta θ(数据生成机制的参数)的时候的损失:
L ( θ , δ ) = △ E ( x , y ) ∼ p ( x , y ∣ θ ) [ l ( y , δ ( x ) ] = ∑ x ∑ y L ( y , δ ( x ) ) p ( x , y ∣ θ ) L(\theta,\delta)\overset\triangle{=} E_{(x,y) \sim p(x,y|\theta)}[l(y,\delta(x)]=\sum_x\sum_y L(y,\delta(x))p(x,y|\theta) L(θ,δ)=△E(x,y)∼p(x,y∣θ)[l(y,δ(x)]=∑x∑yL(y,δ(x))p(x,y∣θ)(5.109)
这就是泛化误差(generalization error).咱们的目标是最小化后验期望损失,即:
ρ ( δ ∣ D ) = ∫ p ( θ ∣ D ) L ( θ , δ ) d θ \rho(\delta|D)=\int p(\theta|D)L(\theta,\delta)d\theta ρ(δ∣D)=∫p(θ∣D)L(θ,δ)dθ(5.110)
这和公式6.47当中定义的频率论中的风险(risk)相对应.
5.7.2 假阳性和假阴性的权衡
本章关注的是二分类决策问题(binary decision problems),比如假设检验(hypothesis testing),二分类,对象事件监测等等.这种情况下就有两种错误类型:假阳性(false positive,也叫假警报false alarm),就是我们估计的 y ^ = 1 \hat y=1 y^=1而实际上真实的是 y = 0 y=0 y=0;或者就是假阴性(false negative,也叫做漏检测missed detection),就是我们估计的是 y ^ = 0 \hat y=0 y^=0而实际上真实的是 y = 1 y=1 y=1.0-1损失函数同等对待这两种错误.可以用下面这个更通用的损失矩阵来表征这种情况:
| \hat y=1 | \hat y=0 | |
|---|---|---|
| y=1 | 0 | L F N L_{FN} LFN |
| y=0 | L F P L_{FP} LFP | 0 |
上面的 L F N L_{FN} LFN就是假阴性的损失,而 L F P L_{FP} LFP是假阳性的损失.两种可能性微的后验期望损失为:
ρ ( y ^ = 0 ∣ x ) = L F N p ( y = 1 ∣ x ) (5.111) ρ ( y ^ = 1 ∣ x ) = L F P p ( y = 0 ∣ x ) (5.112) \begin{aligned} \rho(\hat y=0|x)&= L_{FN} p(y=1|x) &\text{(5.111)}\\ \rho(\hat y=1|x)&= L_{FP} p(y=0|x) &\text{(5.112)}\\ \end{aligned} ρ(y^=0∣x)ρ(y^=1∣x)=LFNp(y=1∣x)=LFPp(y=0∣x)(5.111)(5.112)
因此应选 y ^ = 1 \hat y=1 y^=1 当且仅当:
ρ ( y ^ = 0 ∣ x ) > ρ ( y ^ = 1 ∣ x ) (5.113) p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) > L F P L F N (5.114) \begin{aligned} \rho(\hat y=0|x) &> \rho(\hat y=1|x)&\text{(5.113)}\\ \frac{p(y=1|x) }{p(y=0|x) }&>\frac{L_{FP}}{L_{FN}} &\text{(5.114)}\\ \end{aligned} ρ(y^=0∣x)p(y=0∣x)p(y=1∣x)>ρ(y^=1∣x)>LFNLFP(5.113)(5.114)
如果 L F N = c L F P L_{FN}=cL_{FP} LFN=cLFP,很明显(如练习5.10所示)应该选 y ^ = 1 \hat y=1 y^=1,当且仅当$p(y=1|x)/p(y=0|x)> \tau , 其中的 ,其中的 ,其中的\tau=c/(1+c) ( 更多细节参考 M u l l e r e t a l . 2004 ) . 例如 , 如果一个假阴性的损失是假阳性的两倍 , 就设 (更多细节参考 Muller et al. 2004).例如,如果一个假阴性的损失是假阳性的两倍,就设 (更多细节参考Mulleretal.2004).例如,如果一个假阴性的损失是假阳性的两倍,就设c=2$,然后在宣称预测结果为阳性之前要先使用一个2/3的决策阈值(decision threshold).
接下来要讨论的是ROC曲线,这种方式提供了学习FP-FN权衡的一种方式,而不用必须去选择特定的阈值设置.
5.7.2.1 ROC 曲线以及相关内容
| 真实1 | 真实0 | Σ \Sigma Σ | |
|---|---|---|---|
| 估计1 | TP真阳性 | FP假阳性 | N ^ + = T P + F P \hat N_{+} =TP+FP N^+=TP+FP |
| 估计0 | FN假阴性 | TN真阴性 | N ^ − = F N + T N \hat N_{-} =FN+TN N^−=FN+TN |
| Σ \Sigma Σ | N + = T P + F N N_{+} =TP+FN N+=TP+FN | N − = F P + T N N_{-}=FP+TN N−=FP+TN | N = T P + F P + F N + T N N = TP + FP + FN + TN N=TP+FP+FN+TN |
表5.2 从混淆矩阵(confusion matrix)可推导的量. N + N_+ N+是真阳性个数, N ^ + \hat N_{+} N^+是预测阳性个数, N − N_- N−是真阴性个数, N ^ − \hat N_{-} N^−是预测阴性个数.
| y = 1 y=1 y=1 | y = 0 y=0 y=0 | |
|---|---|---|
| y ^ = 1 \hat y=1 y^=1 | T P / N + = T P R = s e n s i t i v i t y = r e c a l l TP/N_+=TPR=sensitivity=recall TP/N+=TPR=sensitivity=recall | F P / N − = F P R = t y p e I FP/N_− =FPR=type I FP/N−=FPR=typeI |
| y ^ = 0 \hat y=0 y^=0 | F N / N + = F N R = m i s s r a t e = t y p e I I FN/N_+ =FNR=miss rate=type II FN/N+=FNR=missrate=typeII | T N / N − = T N R = s p e c i fi t y TN/N_− =TNR=specifity TN/N−=TNR=specifity |
表5.3 从一个混淆矩阵中估计 p ( y ^ ∣ y ) p(\hat y|y) p(y^∣y).缩写解释:FNR = false negative rate 假阴性率, FPR = false positive rate 假阳性率, TNR = true negative rate 真阴性率, TPR = true positive rate 真阳性率.
如果 f ( x ) > τ f(x)>\tau f(x)>τ是决策规则,其中的 f ( x ) f(x) f(x)是对 y = 1 y=1 y=1(应该与 p ( y = 1 ∣ x ) p(y = 1|x) p(y=1∣x)单调相关,但不必要是概率函数)的信心的衡量, τ \tau τ是某个阈值参数.对于每个给定的 τ \tau τ值,可以应用局Ce规则,然后统计真阳性/假阳性/真阴性/假阴性的各自出现次数,如表5.2所示./这个误差表格也叫作混淆矩阵(confusion matrix).
从这个表中可以计算出真阳性率(TPR),也叫作敏感度(sensitivity)/识别率(recall)/击中率(hit rate),使用 T P R = T P / N + ≈ p ( y ^ = 1 ∣ y = 1 ) TPR = TP/N_+ \approx p(\hat y = 1|y = 1) TPR=TP/N+≈p(y^=1∣y=1)就可以计算得到.还可以计算假阴性率(FPR),也叫作误报率(false alarm rate)/第一类错误率(type I error rate),利用 F P R = F P / N − ≈ p ( y ^ = 1 ∣ y = 0 ) FPR = FP/N_− \approx p(\hat y = 1|y = 0) FPR=FP/N−≈p(y^=1∣y=0).这些定义以及相关概念如表格5.3和5.4所示.在计算损失函数的时候可以任意组合这些误差.
不过,与其使用某个固定阈值 τ \tau τ来计算真阳性率TPR和假阳性率FPR,还不如使用一系列的阈值来运行监测器,然后投影出TPR关于FPR的曲线,作为 τ \tau τ的隐含函数.这也叫受试者工作特征曲线(receiver operating characteristic curve,简称ROC曲线),又称为感受性曲线(sensitivity curve),如图5.15(a)就是一例.任何系统都可以设置阈值为1即 τ = 1 \tau =1 τ=1来实现左下角的点(FPR = 0, TPR = 0),这样也就是所有的都分类成为阴性了;类似的也可以设置阈值为0即 τ = 0 \tau =0 τ=0,都跑到右上角去,即(FPR = 1, TPR = 1),也就是都分类成阳性.如果一个系统在概率层面(chance level)上运行,就可以通过选择适当阈值来实现对角线上的 T P R = F P R TPR = FPR TPR=FPR的任一点.一个能够完美区分开阴性阳性的系统的阈值可以使得整个出在图的左上方,即(FPR = 0, TPR = 1);通过变换阈值,这样的系统就可以从左边的轴移动到顶部轴,如图5.15(a)所示.
一个ROC曲线的质量通常用一个单一数值来表示,也就是曲线所覆盖的面积(area under the curve,缩写为AUC).AUC分数越高就越好,最大的显然就是1了.另外一个统计量是相等错误率(equal error rate,缩写为EER),也叫做交错率(cross over rate),定义是满足FPR = FNR的值.由于FNR=1-TPR,所以可以画一条线从左上角到右下角然后看在哪里切穿ROC曲线就是了(参考图5.15(a)中的A和B两个点).EER分数越低越好,最小显然就是0.
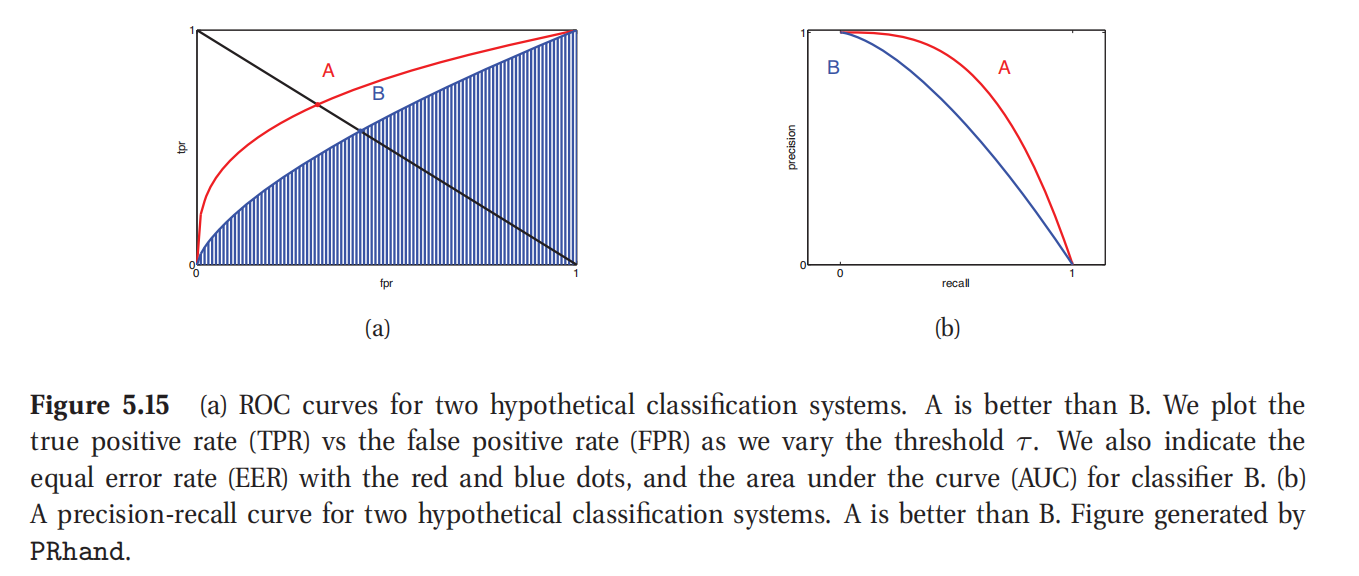
此处查看原书图5.15
| y = 1 y=1 y=1 | y = 0 y=0 y=0 | |
|---|---|---|
| y ^ = 1 \hat y=1 y^=1 | T P / N ^ + = p r e c i s i o n = P P V TP/\hat N_+=precision =PPV TP/N^+=precision=PPV | F P / N ^ + = F D P FP/\hat N_+ =FDP FP/N^+=FDP |
| y ^ = 0 \hat y=0 y^=0 | F N / N ^ − FN/\hat N_- FN/N^− | T N / N ^ − = N P V TN/\hat N_− =NPV TN/N^−=NPV |
表5.4 从一个混淆矩阵中估计的量.缩写解释:FDP = false discovery probability 错误发现概率, NPV = negative predictive value 阴性预测值, PPV = positive predictive value阳性预测值.
5.7.2.2 精确率-识别率曲线(Precision recall curves)
探测小概率的罕见事件(比如检索相关文档或在图中查找面孔)时候,阴性结果的数量会非常大.这样再去对比真阳性率 T P R = T P / N + TPR = TP/N_+ TPR=TP/N+和假阳性率 F P R = F P / N − FPR = FP/N_− FPR=FP/N−就没啥用处了,因为假阳性率FPR肯定会很小的.因此在ROC曲线上的所有行为都会出现在最左边.这种情况下,通常就把真阳性率TPR和假阳性个数投一个曲线,而不用假阳性率FPR.
不过有时候"阴性(negative)"还不太好定义.例如在图像中探测一个对象(参考本书1.2.1.3),如果探测器通过批量分块来进行探测,那么分块检验过的数目,也就是真阴性的数目,是算法的一个参数,而并不是问题本身定义的一部分.所以就要用一个只涉及阳性的概念来衡量.(注:这样就是问题定义控制的,而不是算法决定了.)
精确率(precision)的定义是 T P / N ^ + = p ( y = 1 ∣ y ^ = 1 ) TP/\hat N_+ =p(y=1|\hat y=1) TP/N^+=p(y=1∣y^=1),识别率(recall)的定义是 T P / N + = p ( y ^ = 1 ∣ y = 1 ) TP/N_+ =p(\hat y=1|y=1) TP/N+=p(y^=1∣y=1).精确率衡量的是检测到的阳性中有多大比例是真正的阳性,而识别率衡量的是在阳性中有多少被我们检测到了.如果 y ^ i ∈ { 0 , 1 } \hat y_i \in \{0,1\} y^i∈{0,1}是预测的分类标签,而 y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1}是真实分类标签,就可以估计精确率和识别率,如下所示:
P = ∑ i y i y ^ i ∑ i y ^ i , R = ∑ i y i y ^ i ∑ i y i P=\frac{\sum_i y_i\hat y_i}{\sum_i \hat y _i}, R= \frac{\sum_iy_i\hat y_i}{\sum_i y_i} P=∑iy^i∑iyiy^i,R=∑iyi∑iyiy^i(5.115)
精确率-识别率曲线(precision recall curves)就是随着阈值参数 τ \tau τ的变化对精确率与识别率直接的关系投图得到的曲线.如图5.15(b)所示.在图中曲线尽量往右上角去就好了.
这个曲线可以用一个单一数值来概括,也就是均值精确率(mean precision,在识别到的值上求平均值),近似等于曲线下的面积.或者也可以用固定识别率下的精确率来衡量,比如在前K=10个识别到的项目中的精确率.这就叫做在K分数(K score)的平均精确率.这个指标在评估信息检索系统的时候用得很广.
| Class 1 | Class 2 | Pooled | ||||||
|---|---|---|---|---|---|---|---|---|
| y = 1 y=1 y=1 | y = 0 y=0 y=0 | y = 1 y=1 y=1 | y = 0 y=0 y=0 | y = 1 y=1 y=1 | y = 0 y=0 y=0 | |||
| y ^ = 1 \hat y=1 y^=1 | 10 | 10 | y ^ = 1 \hat y=1 y^=1 | 90 | 10 | y ^ = 1 \hat y=1 y^=1 | 100 | 20 |
| y ^ = 0 \hat y=0 y^=0 | 10 | 970 | y ^ = 0 \hat y=0 y^=0 | 10 | 890 | y ^ = 0 \hat y=0 y^=0 | 20 | 1860 |
表5.5 展示了宏观和微观平均的区别.y是真实类别标签, y ^ \hat y y^是名义标签(called label).在这个样例里面,宏观平均精确率是 [ 10 / ( 10 + 10 ) + 90 / ( 10 + 90 ) ] / 2 = ( 0.5 + 0.9 ) / 2 = 0.7 [10/(10 + 10) + 90/(10 + 90)]/2 = (0.5 + 0.9)/2 = 0.7 [10/(10+10)+90/(10+90)]/2=(0.5+0.9)/2=0.7.微观平均精确率是 100 / ( 100 + 20 ) ≈ 0.83 100/(100 + 20) \approx 0.83 100/(100+20)≈0.83.此表参考了(Manning et al. 2008)的表格13.7.
5.7.2.3 F分数(F-scores)*
对于固定阈值,可以计算单个的精确率和识别率的值.然后可以用这些值来计算出一个单个的统计量,就是F分数(F score),也叫做 F 1 F_1 F1分数( F 1 F_1 F1 score),是精确率和识别率的调和均值(harmonic mean):
$F_1 \overset\triangle{=} \frac{2}{1/P+1/R} =\frac{2PR}{R+P} $(5.116)
使用等式5.115,就可以把上面的式子写成下面的形式:
F 1 = 2 ∑ i = 1 N y i y ^ i ∑ i = 1 N y i + ∑ i = 1 N y ^ i F_1 =\frac{2\sum^N_{i=1}y_i \hat y_i}{\sum^N_{i=1}y_i+\sum^N_{i=1}\hat y_i} F1=∑i=1Nyi+∑i=1Ny^i2∑i=1Nyiy^i(5.117)
这个量在信息检索测量里面用得很广泛.
要理解为啥用调和均值(harmonic mean)而不用算数均值(arithmetic mean) ( P + R ) / 2 (P + R)/2 (P+R)/2,可以考虑下面的情况.设识别了全部的项目,也就是识别率 R = 1 R=1 R=1.精确率可以通过有效率(prevalence) p ( y = 1 ) p(y=1) p(y=1)来得到.加入有效率很低,比如 p ( y = 1 ) = 1 0 − 4 p(y=1)=10^{-4} p(y=1)=10−4.这时候P和R的算数均值为 ( P + R ) / 2 = ( 1 0 − 4 + 1 ) / 2 ≈ 50 % (P + R)/2 = (10^{−4} + 1)/2 \approx 50\% (P+R)/2=(10−4+1)/2≈50%.与之相对,调和均值则为 2 × 1 0 − 4 × 1 1 + 1 0 − 4 ≈ 0.2 % \frac{2\times 10^{-4}\times 1}{1+10^{-4}}\approx 0.2\% 1+10−42×10−4×1≈0.2%.
在多类情况下(比如文档分类问题),有两种办法来泛化 F 1 F_1 F1分数.第一种就叫宏观平均F1分数(macro-averaged F1),定义是 ∑ c = 1 C F 1 ( c ) / C \sum^C_{c=1}F_1(c)/C ∑c=1CF1(c)/C,其中的 F 1 ( c ) F_1(c) F1(c)是将类别c与其他分类区分开这个过程的F1分数.另一重定义叫微观平均F1分数(micro-averaged F1),定义是将每个类的情形分析表(contingency table)集中所有计数的F1分数.
表5.5给出了一个样例,可以比对这两种平均F1分数的区别.可见类别1的精确率是0.5,类别2是0.9.宏观平均精确率就是0.7,而微观平均精确率是0.83.后面这个更接近类别2的精确率而远离类别1的精确率,这是因为类别2是类别1的五倍.为了对每个类给予同样的权重,就要用宏观平均.
5.7.2.4 错误发现率(False discovery rates)*
假设要用某种高通量(high throughput)测试设备去发现某种罕见现象,比如基因在微观上的表达,或者射电望远镜等等.就需要制造很多二进制决策.形式为 p ( y i = 1 ∣ D ) > τ p(y_i =1|D)>\tau p(yi=1∣D)>τ,其中的 D = { x i } i = 1 N D=\{x_i\}^N_{i=1} D={xi}i=1N,N 可能特别大.这种情况也叫做多重假设检验(multiple hypothesis testing).要注意这和标准的二分类问题的不同之处在于是要基于全部数据而不仅仅是 x i x_i xi来对 y i y_i yi进行分类.所以这是一个同时分类问题(simultaneous classification problem),这种问题下我们就希望能比一系列独立分类问题有更好的效果.
该怎么设置阈值
τ
\tau
τ呢?很自然的方法是尽量降低假阳性的期望个数.在贝叶斯方法中,可以用下面的方式计算:
F
D
(
τ
,
D
)
=
△
∑
i
(
1
−
p
i
)
I
(
p
i
>
τ
)
FD(\tau,D)\overset\triangle{=} \sum_i (1-p_i)I(p_i>\tau)
FD(τ,D)=△∑i(1−pi)I(pi>τ)(5.118)
(
1
−
p
i
)
:
p
r
.
e
r
r
o
r
(1-p_i): pr. error
(1−pi):pr.error
$I(p_i>\tau): discovery $
其中的 p i = △ p ( y i = 1 ∣ D ) p_i\overset\triangle{=}p(y_i=1|D) pi=△p(yi=1∣D)是你对目标物体会表现出问题中情形的信心.用如下方式定义后验期望错误发现率(posterior expected false discovery rate):
F D R ( τ , D ) = △ F D ( τ , D ) / N ( τ , D ) FDR(\tau,D)\overset\triangle{=} FD(\tau ,D)/N(\tau,D) FDR(τ,D)=△FD(τ,D)/N(τ,D)(5.119)
上式中的 N ( τ , D ) = ∑ i I ( p i > τ ) N(\tau,D)=\sum_i I(p_i>\tau) N(τ,D)=∑iI(pi>τ),是发现项目数.给定一个理想的错误发现率(FDR)的容忍度(tolerance),比如 α = 0.05 \alpha =0.05 α=0.05,就可以调整 τ \tau τ来实现这个要求l这也叫做控制错误发现率(FDR)的直接后验概率手段(direct posterior probability approach),参考(Newton et al. 2004; Muller et al. 2004).
为了控制错误发现率FDR,更有帮助对方法是联合起来估计各个 p i p_i pi(比如可以使用本书5.5当中提到的分层贝叶斯模型),而不是单独估计.这样可以汇集统计强度,从而降低错误发现率(FDR).更多内容参考(Berry and Hochberg 1999).
5.7.3 其他话题*
这一部分讲一点和贝叶斯决策规则相关的其他主题.这就没地方去详细讲了,不过也都给出了参考文献啥的,读者可以自己去进一步学习.
5.7.3.1 情境强盗(Contextual bandits)
单臂强盗(one-armed bandit)是对老虎机(slot machine)的俗称,这东西在赌场中很常见.游戏是这样的:你投进去一些钱,然后拉动摇臂,等到机器停止运转;如果你很幸运,就会赢到钱.现在加入有K个这样的机器可选.那你该选哪个呢?这就叫做一个多臂强盗(multi-armed bandit),就可以用贝叶斯决策理论来建模了:有K个可能的行为,然后每个都有位置的奖励(支付函数,payoff function) r k r_k rk.建立并维护一个置信状态(belief state) p ( r 1 : K ∣ D ) = ∏ k p ( r k ∣ D ) p(r_{1:K}|D)=\prod_k p(r_k|D) p(r1:K∣D)=∏kp(rk∣D),就可以推出一个最优策略了;这可以通过编译成一系列的吉廷斯指数(Gittins Indices ,参考 Gittins 1989).这个优化解决了探索-利用之间的权衡(exploration-exploitation tradeoff),这一均衡决定了在决定随着胜者离开之前要将每个行为尝试多少次.
然后考虑扩展情况,每个摇臂以及每个玩家,都有了一个对应的特征向量;就叫x吧.这个情况就叫做情境强盗(contextual bandit 参考Sarkar 1991; Scott 2010; Li et al. 2011).比如这里的手臂可以指代要展示给用户的广告或者新闻文章,而特征向量表示的是这些广告或者文章的性质,比如一个词汇袋,也可以表示用户的性质,比如人口统计信息.如果假设奖励函数有一个线性模型, r k = θ k T x r_k=\theta ^T_k x rk=θkTx,就可以构建一个每个摇臂的参数的分布 p ( θ k ∣ D ) p(\theta_k|D) p(θk∣D),其中的D是一系列的元组(tuples),形式为 ( a , x , r ) (a,x,r) (a,x,r),制定对应的要比是否被拉动,以及其他特征是什么,还有就是输出的结果是什么(如果用户点击广告了就令 r = 1 r=1 r=1,否则令 r = 0 r=0 r=0).后面的章节中,我们会讲从线性和逻辑回归模型来计算 p ( θ k ∣ D ) p(\theta_k|D) p(θk∣D)的各种方法.
给定了一个后验,我们必须决定对应采取的行动.常见的一种期发放时,也叫做置信上界(upper confidence bound,缩写为UCB)的思路是要采取能够将下面这个项目最大化的行为:
KaTeX parse error: Got function '\overset' with no arguments as superscript at position 3: K^\̲o̲v̲e̲r̲s̲e̲t̲\triangle{=}\ar…(5.120)
上式中 μ k = E [ r k ∣ D ] , σ k 2 = v a r [ r k ∣ D ] \mu_k=E[r_k|D],\sigma_k^2=var[r_k|D] μk=E[rk∣D],σk2=var[rk∣D],而 λ \lambda λ是一个调节参数,在探索(exploration)和利用(exploitation)之间进行权衡.指关节度就是应该选择我们觉得会有好结果的行为( μ k \mu_k μk大),以及/或者选择我们不太确定的行为( σ k \sigma_k σk大).
还有个更简单的方法,叫做汤姆森取样(Thompson sampling),如下所述.每一步都选择一个概率等于成为最优行为选择概率的行为k:
p k = ∫ I ( E [ r ∣ a , x , θ ] = max a ′ E [ r ∣ a ′ , x , θ ] ) p ( θ ∣ D ) d θ p_k =\int I( E[r|a,x,\theta]=\max _{a'} E[r|a',x,\theta])p(\theta|D)d\theta pk=∫I(E[r∣a,x,θ]=maxa′E[r∣a′,x,θ])p(θ∣D)dθ(5.121)
可以简单地从后验 θ t ∼ p ( θ ∣ D ) \theta_t\sim p(\theta|D) θt∼p(θ∣D)中取出单一样本来对此进行估计,然后选择 k ∗ = arg max k E [ r ∣ x , k , θ t ] k^* =\arg\max_k E[r|x,k,\theta^t] k∗=argmaxkE[r∣x,k,θt].这个方法不仅简单,用起来效果还不错(Chapelle and Li 2011).
5.7.3.2 效用理论(Utility theory)
假设你是一个医生,要去决定是不是对一个病人做手术.设想这个病人有三种状态:没有癌症/罹患肺癌/罹患乳腺癌.由于行为和状态空间都是连续的,就可以按照下面这个损失矩阵(loss matrix)来表达损失函数 L ( θ , a ) L(\theta,a) L(θ,a):
| 做手术 | 不做手术 | |
|---|---|---|
| 没有癌症 | 20 | 0 |
| 肺癌 | 10 | 50 |
| 乳腺癌 | 10 | 60 |
这些数字表明,当病人有癌症的时候不去做手术是很不好的(取决于不同类型的癌症,损失在50-60),因为病人可能因此而去世;当病人没有患上癌症的时候不进行手术就没有损失(0);没有癌症还手术就造成了浪费(损失为20);而如果患上了癌症进行手术虽然痛苦但必要(损失10).
很自然咱们要去考虑一下这些数字是从哪里来的.本质上这些数字代表了一个冒险医生的个人倾向或者价值观,甚至可能有点任意性:有的人可能喜欢巧克力冰淇淋,而有人喜欢香草口味,这类情况下并没有正确/损失/效用函数等等.可是也有研究(DeGroot 1970)表明,任意一组的持续倾向都可以转换成一个标量的损失/效用函数.这里要注意,这个效用可以用任意的尺度来衡量,比如美元啊等等,反正只和对应情况下有影响的值相关.
5.7.3.3 序列决策理论(Sequential decision theory)
之前我们讲的都是单次决策问题(one-shot decision problems),就是每次都是做出一个决策然后就游戏结束了.在本书10.6,我们会把这个繁华到多阶段或者序列化的决策问题上.这些问题在很多商业和工程背景下都会出现.这些内容和强化学习的内容紧密相关.不过这方面的进一步讨论超出了本书的范围了.
练习略.
),如下所述.每一步都选择一个概率等于成为最优行为选择概率的行为k:
p k = ∫ I ( E [ r ∣ a , x , θ ] = max a ′ E [ r ∣ a ′ , x , θ ] ) p ( θ ∣ D ) d θ p_k =\int I( E[r|a,x,\theta]=\max _{a'} E[r|a',x,\theta])p(\theta|D)d\theta pk=∫I(E[r∣a,x,θ]=maxa′E[r∣a′,x,θ])p(θ∣D)dθ(5.121)
可以简单地从后验 θ t ∼ p ( θ ∣ D ) \theta_t\sim p(\theta|D) θt∼p(θ∣D)中取出单一样本来对此进行估计,然后选择 k ∗ = arg max k E [ r ∣ x , k , θ t ] k^* =\arg\max_k E[r|x,k,\theta^t] k∗=argmaxkE[r∣x,k,θt].这个方法不仅简单,用起来效果还不错(Chapelle and Li 2011).
5.7.3.2 效用理论(Utility theory)
假设你是一个医生,要去决定是不是对一个病人做手术.设想这个病人有三种状态:没有癌症/罹患肺癌/罹患乳腺癌.由于行为和状态空间都是连续的,就可以按照下面这个损失矩阵(loss matrix)来表达损失函数 L ( θ , a ) L(\theta,a) L(θ,a):
| 做手术 | 不做手术 | |
|---|---|---|
| 没有癌症 | 20 | 0 |
| 肺癌 | 10 | 50 |
| 乳腺癌 | 10 | 60 |
这些数字表明,当病人有癌症的时候不去做手术是很不好的(取决于不同类型的癌症,损失在50-60),因为病人可能因此而去世;当病人没有患上癌症的时候不进行手术就没有损失(0);没有癌症还手术就造成了浪费(损失为20);而如果患上了癌症进行手术虽然痛苦但必要(损失10).
很自然咱们要去考虑一下这些数字是从哪里来的.本质上这些数字代表了一个冒险医生的个人倾向或者价值观,甚至可能有点任意性:有的人可能喜欢巧克力冰淇淋,而有人喜欢香草口味,这类情况下并没有正确/损失/效用函数等等.可是也有研究(DeGroot 1970)表明,任意一组的持续倾向都可以转换成一个标量的损失/效用函数.这里要注意,这个效用可以用任意的尺度来衡量,比如美元啊等等,反正只和对应情况下有影响的值相关.
5.7.3.3 序列决策理论(Sequential decision theory)
之前我们讲的都是单次决策问题(one-shot decision problems),就是每次都是做出一个决策然后就游戏结束了.在本书10.6,我们会把这个繁华到多阶段或者序列化的决策问题上.这些问题在很多商业和工程背景下都会出现.这些内容和强化学习的内容紧密相关.不过这方面的进一步讨论超出了本书的范围了.
练习略.






















 419
419











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








